Просмотр содержимого документа
«Урок геометрии в 8 классе по теме "Равновеликие фигуры"»
Урок геометрии в 8 классе по теме "РАВНОВЕЛИКИЕ ФИГУРЫ"
Цели урока:
Введение понятия равновеликих фигур, вывод формул площади параллелограмма и треугольника; формирование конструктивного мышления, умений и навыков решения задач на применение введённых понятий и формул площадей;
Формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры; развитие навыков самостоятельной работы.
Воспитание культуры личности, отношения к математике, воспитание ответственного отношения к учебному труду.
Оборудование: Мультимедиа проектор, ножницы, угольники, линейки, модели произвольных треугольников, простые карандаши, квадрат «Танграм» (всего 15 комплектов); кусочки двустороннего скотча для наклеивания частей фигуры; листы белой бумаги; демонстрационный материал – решение задачи.
ХОД УРОКА
I. Организационный момент
Учитель: Как вы думаете, какова цель сегодняшнего урока? (учащиеся формулируют цель урока).
Ещё можно дополнить сформулированную цель урока следующим: познакомится с понятием равносоставленных фигур, вывести формулы площадей параллелограмма и треугольника.
Сообщение темы и цели урока.
II. Формирование новых понятий и способов действий
| 1. Введение понятия равносоставленных и равновеликих фигур. А начнём мы изучать новый материал с решения проблемы. |
| 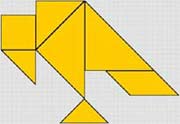
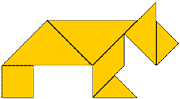
| На экране одноцветная фигура «Танграм» [1] Вопрос. Как найти площадь данной фигуры, изображающей силуэт птицы? Возможный вариант ответа: Разрезать данную фигуру на известные геометрические фигуры, найти сумму их площадей. Учитель. Да, вы правы, необходимо, разрезать эту «птицу» на известные геометрические фигуры, и попытаться найти площадь каждой. Действия учителя. Учитель разбирает «птицу» на части и меняет их цвет. |
| 
| Вопрос. Теперь мы видим, что эта фигура являлась «хитроумным узором из семи частей», но возникает опять проблема: как, же нам вычислить площадь каждой части, если нам известна только формула площади квадрата или прямоугольника? Возможный вариант ответа: Необходимо попытаться собрать эти семь частей в квадрат. Учитель. Да, действительно, необходимо собрать эти семь фигур в квадрат, называемый в древнем Китае «Доска Мудрости». Действия учителя. Учитель собирает семь геометрических фигур в квадрат. Учитель. Мы только, что увидели, что и данная фигура, и квадрат составлены из одних и тех же геометрических фигур. |
| Такие фигуры называются равносоставленными. А что вы можете сказать о площадях этих фигур? Да, площади равносоставленных фигур равны, а фигуры, имеющие равные площади называются равновеликими. Вывод. Из всего вышесказанного можно сформулировать свойство площади: если фигура составлена из нескольких фигур, то её площадь равна сумме площадей этих фигур. |
| 2. Вывод формул площадей параллелограмма и треугольника. 1) Вывод формулы площади параллелограмма. |
| 
| Учитель. Используя, выше сформулированное свойство площади, выведем формулы площадей параллелограмма. Для этого «перекроим» параллелограмм в прямоугольник. Учитель в этой же программе составляет из параллелограмма прямоугольник. Вопрос. С помощью, какой формулы можно вычислить площадь параллелограмма? Ответ. S = ah. Площадь параллелограмма равна произведению высоты и стороны, к которой, проведена эта высота. |
| Замечание. В случае необходимости, в этом же кадре, начертить параллелограмм и провести его высоту. |
| 2) Вывод формулы площади треугольника. Работа в парах. Творческое задание «Голова хорошо, а две – лучше». Разрежьте треугольник на части и составьте из них прямоугольник. Сделайте вывод о формуле площади этого треугольника. |
| 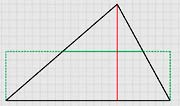
| Задание. Объясните способ разрезания треугольника на части. Варианты ответа. 1. Опустить высоту из вершины треугольника к противолежащей стороне. 2. Провести среднюю линию треугольника, соединяющую середины двух других сторон. Эта средняя линия отсечёт от данного треугольника два треугольника, которые необходимо отрезать и приставить к третьей стороне рассматриваемого треугольника. |
| 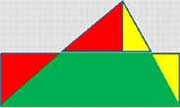
| Действия учителя. На экране демонстрируется решение данной задачи. Вывод: Площадь треугольника равна половине произведения его высоты и стороны, на которую опущена эта высота. S = 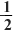 ah. ah. |
|
|
III. Применение знаний, формирование умений и навыков
| 3. Групповая работа. «Сообща и дело спорится». Задания на нахождение площадей фигур. |
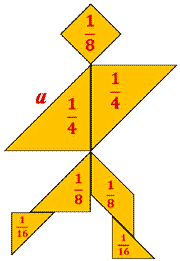
| I группа Найдите площадь каждого тана фигурки танграма, используя формулы площадей фигур. Результаты округляйте до целых. | I группа
Найдите площадь каждого тана фигурки танграма, предварительно решив задачи (результаты округляйте до целых): 1. Какую часть составляет один тан от всего квадрата? 2. Найдите площадь всего квадрата из которого составлена фигурка Танграм |
| 
| 
|
| Sвсего квадрата = a2 = 9.52 90 (см)2 Sбольшого треугольника 21.5 (см)2 Sср. треугольника = Sпар. = Sквадрата 11(см)2 Sмаленького треугольника 5 (см)2 | Sвсего квадрата = a2 = 9.52 90 (см)2 Sбольшого треугольника = 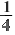 a2= a2= 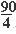 = 22.5 (см)2 = 22.5 (см)2 Sср. треугольника = Sпар. = Sквадрата =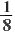 a2 = a2 = 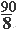 = 11 (см)2 = 11 (см)2 Sмаленького треугольника = 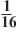 a2 = a2 = 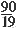 = 6 (см)2 = 6 (см)2 |
| Коллективная проверка выполнения задания. Участники сообщают свои результаты, рассказывают приёмы решения поставленной задачи.. |
IV. Первичный контроль за усвоением знаний
| Практическая работа «Где руки и охота, там спорая работа». Задание. Соберите одну фигурку «Танграм» (таны крепите двухсторонним скотчем на лист белой бумаги). Выбери задание по силам. |
| 1 вариант | 2 вариант |
| Дал Бог руки, а веревки сам вей! (наудовлетворительно) |
|   
|   
|
| Вопрос: Что вы скажете о фигурах? Ответ: Они равносоставленные. Вопрос: А что вы скажете об их площадях? Ответ: площади равны. Значит фигуры являются равновеликими. |
| V. Итог урока. Скажи мне – и я забуду, Покажи мне – и я запомню, Вовлеки меня – и я пойму. Древняя китайская мудрость.
|





























