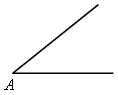
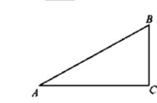
Изложение нового материала в виде лекции Рассмотрим прямоугольный треугольник АВС с прямым углом С (рис.) 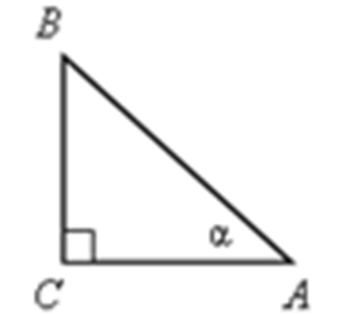 Катет ВС этого треугольника является противолежащим углу А, а катет АС – прилежащим к этому углу. Катет ВС этого треугольника является противолежащим углу А, а катет АС – прилежащим к этому углу. Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. 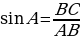 (1) (1) Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. 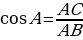 (2) (2) Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету. tg А = 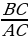 (3) (3)
Из формул (1) и (2) получаем: 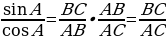 . Сравнивая с формулой (3), находим: tg А = . Сравнивая с формулой (3), находим: tg А =  (4), т.е. тангенс угла равен отношению синуса к косинуса этого угла. (4), т.е. тангенс угла равен отношению синуса к косинуса этого угла. Синус, косинус и тангенс угла равного 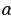 , обозначаются символами , обозначаются символами 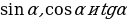 (читается: «синус альфа», «косинус альфа», и «тангенс альфа»). (читается: «синус альфа», «косинус альфа», и «тангенс альфа»). Творческая работа Решить самостоятельно обсуждая в парах, задачу: Докажите, что если острый угол прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны и тангенсы этих углов равны. В самом деле, пусть АВС и 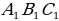 – два прямоугольных треугольника с прямыми углами С и – два прямоугольных треугольника с прямыми углами С и 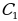 и равными острыми углами А и и равными острыми углами А и 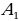 . Треугольники АВС и . Треугольники АВС и 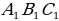 подобны по первому признаку подобия треугольников, поэтому подобны по первому признаку подобия треугольников, поэтому 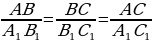 . . Из равенств этих равенств следует, что 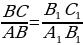 т.е. т.е. 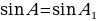 . Аналогично . Аналогично 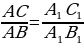 , т.е. , т.е. 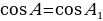 , и , и 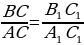 , т.е.tg A = tg , т.е.tg A = tg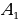 . . Докажем справедливость равенства 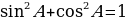 (5) (5) Из формул (1) и (2) получаем 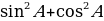 = = 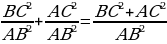 . . По теореме Пифагора 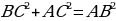 , поэтому , поэтому 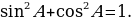 Равенство (5) называется основным тригонометрическим тождеством. Равенство (5) называется основным тригонометрическим тождеством.
| 






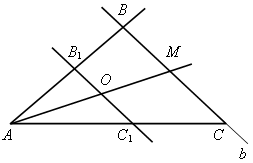
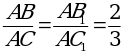 .
.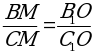 = 1.
= 1. Катет ВС этого треугольника является противолежащим углу А, а катет АС – прилежащим к этому углу.
Катет ВС этого треугольника является противолежащим углу А, а катет АС – прилежащим к этому углу. 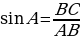 (1)
(1)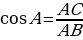 (2)
(2)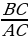 (3)
(3)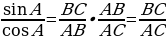 . Сравнивая с формулой (3), находим: tg А =
. Сравнивая с формулой (3), находим: tg А =  (4), т.е. тангенс угла равен отношению синуса к косинуса этого угла.
(4), т.е. тангенс угла равен отношению синуса к косинуса этого угла.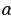 , обозначаются символами
, обозначаются символами 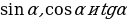 (читается: «синус альфа», «косинус альфа», и «тангенс альфа»).
(читается: «синус альфа», «косинус альфа», и «тангенс альфа»).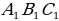 – два прямоугольных треугольника с прямыми углами С и
– два прямоугольных треугольника с прямыми углами С и 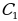 и равными острыми углами А и
и равными острыми углами А и 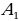 . Треугольники АВС и
. Треугольники АВС и 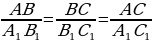 .
.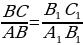 т.е.
т.е. 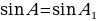 . Аналогично
. Аналогично 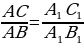 , т.е.
, т.е. 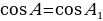 , и
, и 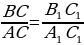 , т.е.tg A = tg
, т.е.tg A = tg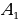 .
.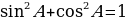 (5)
(5)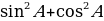 =
= 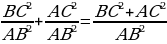 .
.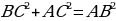 , поэтому
, поэтому 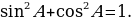 Равенство (5) называется основным тригонометрическим тождеством.
Равенство (5) называется основным тригонометрическим тождеством.
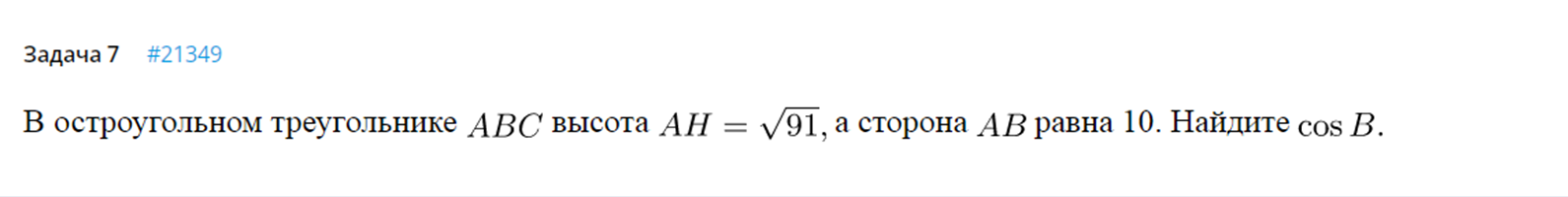
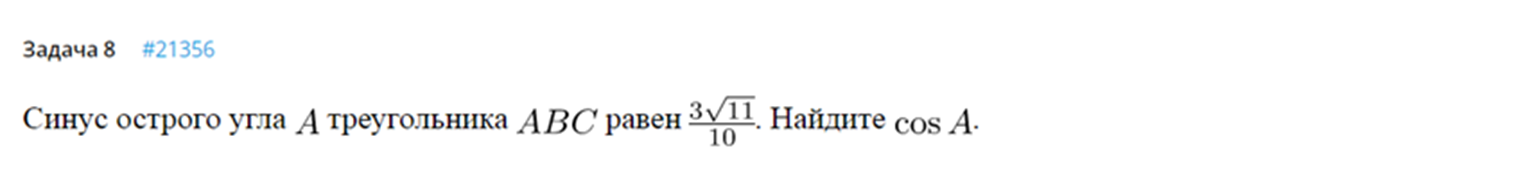

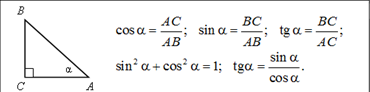
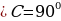 , АВ = 17, ВС=8. Найти:
, АВ = 17, ВС=8. Найти: 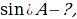
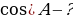 , tg
, tg .
.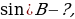
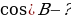 , tg
, tg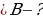 .
.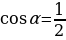 ; б)
; б) 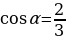 ;
; 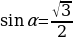 ; г)
; г) 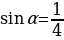 . Найти значение остальных тригонометрических функций.
. Найти значение остальных тригонометрических функций.









