Урок геометрии в 8 классе по теме "Отношение площадей подобных треугольников"

Отношение площадей подобных треугольников

Цель урока: Доказать свойство площадей подобных треугольников и показать его практическую значимость при решении задач.

Задачи урока:

• обучающие – доказать свойство площадей подобных треугольников и показать его практическую значимость при решении задач;

• развивающие – развивать умение анализировать и подбирать аргументацию при решении задачи, способ решения которой неизвестен;

• воспитательные – воспитывать интерес к предмету через содержание учебного процесса и создание ситуации успеха, воспитывать умение работать в группе.

Учащийся владеет следующими знаниями:

1. Определение подобных треугольников.

2. Применение определения подобных треугольников при решении задач.

3. Теорема об отношении площадей треугольников имеющих по равному углу.

Единица деятельностного содержания, которое нужно усвоить учащимся: Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

Ход урока.

1. Организационный момент.

2. Актуализация знаний.

3. Работа с проблемной ситуацией.

4. Подведение итогов урока и запись домашнего задания, рефлексия.

Методы обучения: словесные, наглядные

Формы обучения: фронтальная работа, работа в мини-группы, индивидуальная и самостоятельная работа.

Технологии: задачно-целевая, информационные технологии, компетентностный подход.

Оборудование:

• компьютер, проектор для демонстрации презентации, интерактивная доска,

• компьютерная презентация в MicrosoftPowerPoint;

Ход урока

1. Организационный момент.

Здравствуйте ребята! Мы продолжаем с вами изучать тему «подобие треугольников». Тема нашего урока «Отношение площадей подобных треугольников».

Прежде всего вспомним какие треугольники называются подобными

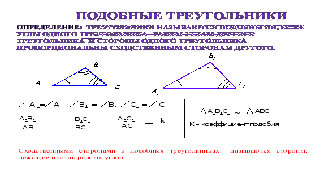
Из этого определения следует ряд важных теорем.

Например: в подобных треугольниках не только сходственные стороны относятся как коэффициент подобия, но и например: высоты, проведенные к сходственным сторонам; медианы, проведенные к сходственным сторонам; периметры подобных треугольников относятся как коэффициент подобия и т. д.

Рассмотрим задачу на отношения периметров подобных треугольников.

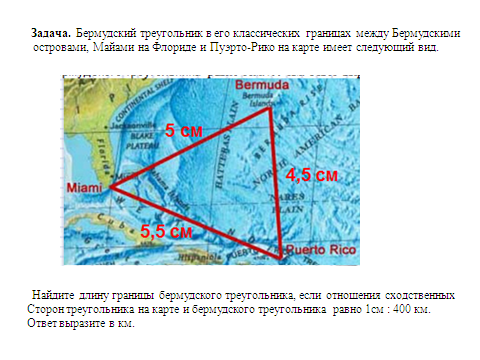
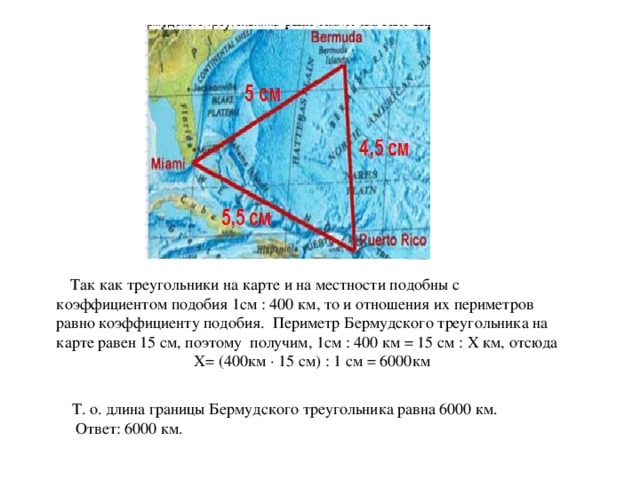
Так как треугольники на карте и на местности подобны с коэффициентом подобия

1см : 400 км, то и отношения их периметров равно коэффициенту подобия. Периметр Бермудского треугольника на карте равен 15 см, поэтому получим,

1см : 400 км = 15 см : Х км, отсюда Х= (400км 15 см) : 1 см = 6000км

Т. о. длина границы Бермудского треугольника равна 6000 км.

Верна ли такая же теорема для площади треугольников?

Выясняется, что с площадями дело обстоит немного иначе, и это продемонстрирует следующая теорема.

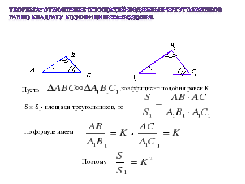
(вставить в доказательство) Т.к. отношение площадей двух треугольников, имеющих по равному углу равно отношению произведения сторон, заключающих равные углы.

Кстати, эту же теорему можно было бы доказать немного по-другому, воспользовавшись тем, что площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию. В этом случае, отношение площадей равно произведению отношения оснований и отношения высот. Отношения высот естественно равно коэффициенту подобия, потому что мы возьмем сходственные стороны в качестве оснований, но, а то, что отношения высот равно коэффициенту подобия, это совсем несложный факт, который также довольно легко доказать. Мы не будем подробно проводить доказательство теоремы таким способом, но я думаю идея ясна.

Разберем несколько примеров, где применяется данная теорема.

Подведем итог сегодняшнего урока. Cегодня мы с вами вспомнили определение подобных треугольников, сформулировали и доказали теорему об отношении площадей подобных треугольников и решили несколько примеров, иллюстрирующих применение данной теоремы. На этом урок закончен.

Геометрия 8 класс

Отношение площадей

подобных треугольников

Землина Елена Владимировна

учитель математики первой категории

МОБУ СОШ №5 МР Мелеузовский район

Республики Башкортостан

А 1

В 1

А

С 1

В

С

Подобные треугольники

Определение : треугольники называются подобными, если углы одного треугольника равны углам другого треугольника и стороны одного треугольника пропорциональны сходственным сторонам другого.

А 1 = А, В 1 = В, С 1 = С

A 1 B 1 C 1 ABC

~

А 1 С 1

А 1 В 1

В 1 С 1

k

K – коэффициент подобия

АС

АВ

ВС

Сходственными сторонами в подобных треугольниках называются стороны, лежащие против равных углов.

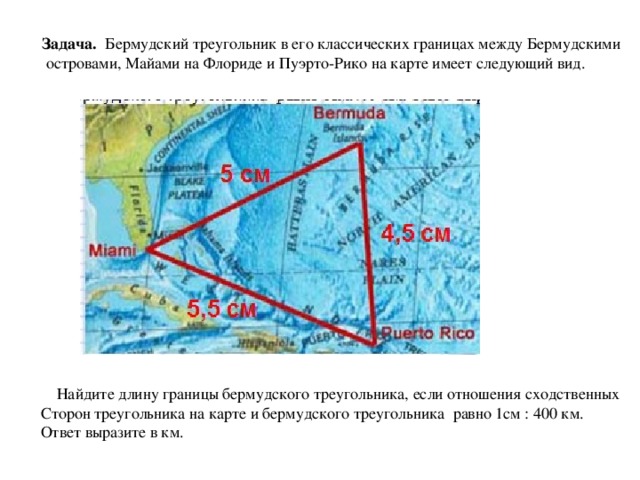
Задача. Бермудский треугольник в его классических границах между Бермудскими

островами, Майами на Флориде и Пуэрто-Рико на карте имеет следующий вид.

Найдите длину границы бермудского треугольника, если отношения сходственных

Сторон треугольника на карте и бермудского треугольника равно 1см : 400 км.

Ответ выразите в км.

Так как треугольники на карте и на местности подобны с коэффициентом подобия 1см : 400 км, то и отношения их периметров равно коэффициенту подобия. Периметр Бермудского треугольника на карте равен 15 см, поэтому получим, 1см : 400 км = 15 см : Х км, отсюда

Х= (400км · 15 см) : 1 см = 6000км

Т. о. длина границы Бермудского треугольника равна 6000 км.

Ответ: 6000 км.

А

А 1

В

В 1

С

С 1

Теорема: Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

,коэффициент подобия равен К

Пусть

S и S 1 - площади треугольников, то

По формуле имеем

и

Поэтому

Задача 1. Пусть даны два подобных треугольника с коэффициентом подобия равным

Чему равно отношение площадей этих треугольников?

Имеем:

( ) 2 = 2

=

Ответ: 2.

А

В

А 1

С

В 1

С 1

Задача2. Пусть даны два подобных треугольника, площади которых соответственно равны 500 см 2 и 125 см 2 . Найдите сторону меньшего треугольника, если сходственная сторона большего треугольника равна 18 см.

125 см 2

500 см 2 ,

А 1 С 1 = 18 см

Найти АС

= 4, значит, к=2.

т.е. к 2 =

, то

Решение: 1) Т. к.

2) Зная, что к=2, найдем

АС

Т. к. отношение подобных сторон равно коэффициенту подобия, то

АС

= А 1 С 1 : к = 18: 2 = 9 (см)

Ответ: 9 см.

Задача 3.

Треугольный дом. Этот дом в форме треугольника расположен в Норвегии. Он выходит окнами на море, и окружен сосновым бором. Снаружи дом полностью обшит деревом, что вкупе с большими окнами прекрасно выглядит на фоне окружающего пейзажа

Площадь участка, который занимает треугольный дом на плане треугольника равна 57, 6 кв. см. Найдите площадь земельного участка, если план выполнен в масштабе 1: 250.

Ответ выразите в кв. м

А

В

С

А 1

В 1

С 1

Площадь участка, который занимает треугольный дом на плане треугольника равна 57, 6 кв. см. Найдите площадь земельного участка, если план выполнен в масштабе 1: 250.

Ответ выразите в кв. м

Ответ: