Урок математики
по теме
«Квадратичная функция,
её график и свойства».
9 класс
Учитель математики
Темерова Лариса Анатольевна
Предмет: математика по теме « Квадратичная функция и ее график» с использованием ИКТ и технологии деятельностного метода обучения в соответствии с ФГОС ООО
Тема: « Квадратичная функция, ее график и свойства»
Продолжительность: 40 минут
Класс: 9 класс
Автор урока - Темерова Лариса Анатольевна- учитель математики
Тип урока: урок обработки умений и рефлексии
Тема: «Квадратичная функция, ее график и свойства»
Цели и задачи урока:
Образовательная:
Развивающая:
развивать наблюдательность, логическое мышление, математическую речь учащихся, умение анализировать и сравнивать, осуществлять дифференцированное развивающее обучение, развивать познавательный интерес к предмету
создать условия для развития навыков самостоятельной работы, развития интеллектуальных качеств: внимания, воображения, памяти, умения обобщать, аргументировать свое мнение.
Воспитательная:
воспитывать коммуникативную культуру учащихся, навыки коллективной деятельности, сотрудничества, взаимопомощи, умение работать в парах
Тип урока:
урок обработки умений и рефлексии
Формируемые результаты:
Предметные: систематизировать знания учащихся о квадратичной функции и её свойствах, навыки применения свойств функции при решении задач;
Личностные: формировать целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики; воспитывать критическое отношение к своим знаниям, учить сравнивать, делать выводы.
Метапредметные: формировать умение использовать приобретенные знания в практической деятельности; формировать умение понимать и использовать математические средства наглядности (таблицы, графики).
Форма организации познавательной деятельности: фронтальная, индивидуальная, работа в парах
Личностные УУД: самоопредление, самовыражение;
Познавательные УУД: целеполагание, анализ, синтез, обобщение, аналогия, самостоятельное выделение и формулирование познавательной цели, поиск и выделение необходимой информации, проблема выбора эффективного способа решения, планирование, выдвижение гипотез и их обоснование, создание способа решения проблемы
Регулятивные УУД: выполнение пробного учебного действия, фиксация индивидуального затруднения, волевая саморегуляция в ситуации затруднения
Коммуникативные УУД: планирование учебного сотрудничества, выражение своих мыслей, использование речевых средств для решения коммуникационных задач, достижение договорённости и согласование общего решения
Оборудование: школьная доска, медиапроектор, компьютер, интерактивная презентация для сопровождения урока, раздаточный материал
Учебник: А. Г. Мерзляк, В. Б. Полонский, М. С. Якир: Алгебра. 9 класс.
Структура и ход урока
Французский писатель Анатоль Франс (1844-1924) однажды заметил: «Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом». Давайте на уроке будем следовать этому совету писателя, будем поглощать знания с большим желанием, ведь они пригодятся вам всегда. Будьте активны и внимательны.
Сегодня мы продолжаем изучать тему и получать знания прошлого урока.
Над чем мы работали ранее? Что мы узнали и изучили на предыдущем уроке?
Давайте попробуем сформулировать тему и цель сегодняшнего урока.
(Учащиеся самостоятельно формулируют тему и цель урока)
Значит у нас урок по теме «Квадратичная функция, ее график и свойства». Повторяем теоретический материал, приводим в систему изученное по данной теме. Ваша задача: показать свои знания, умения и навыки по данной теме при решении задач, при необходимости совершенствовать имеющиеся знания.
Актуализация знаний
Два ученика у доски решают на доске:
первый ученик: №341; второй ученик: №344(1,2).
В это время ещё два ученика решают те же номера, но в тетради.
2. Три ученика работают по карточкам.
Используя шаблон параболы у = х2 построить графики следующих функций:
1. у = -х2 + 4
2. у = (х – 3)2
3. у = х2 - 1
4. у = (х + 5)2
5. у = (х + 2)2 – 1
Работа устно с классом.
1) Повторить теоретический материал по теме “Квадратичная функция”
Какую функцию называют квадратичной?
Какая фигура является графиком квадратичной функции?
По какой формуле можно найти абсциссу вершины параболы �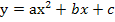 �
�
Каково направление ветвей параболы �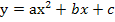 � в зависимости от значения а?
� в зависимости от значения а?
Опиши схему построения графика квадратичной функции
2) Проверка домашней работы (устно): № 342; 346(1,2)
3) Мною неоднократно упоминалось о том, что тема “Квадратичная функция” широко представлена на экзамене (ОГЭ) по математике в 9-ом классе.
Ответь устно на вопросы (презентация)
№1. Указать формулу, которой задаётся квадратичная функция (выбери номер правильного ответа)
�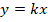 �
�
�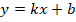 �
�
�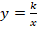 � �
� � �
�
�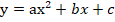 �
�
�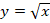 �
�
Ответ: 4
№2. а) Какая из этих графиков не является графом функции?
б) Какая из этих графиков является графиком квадратичной функции?
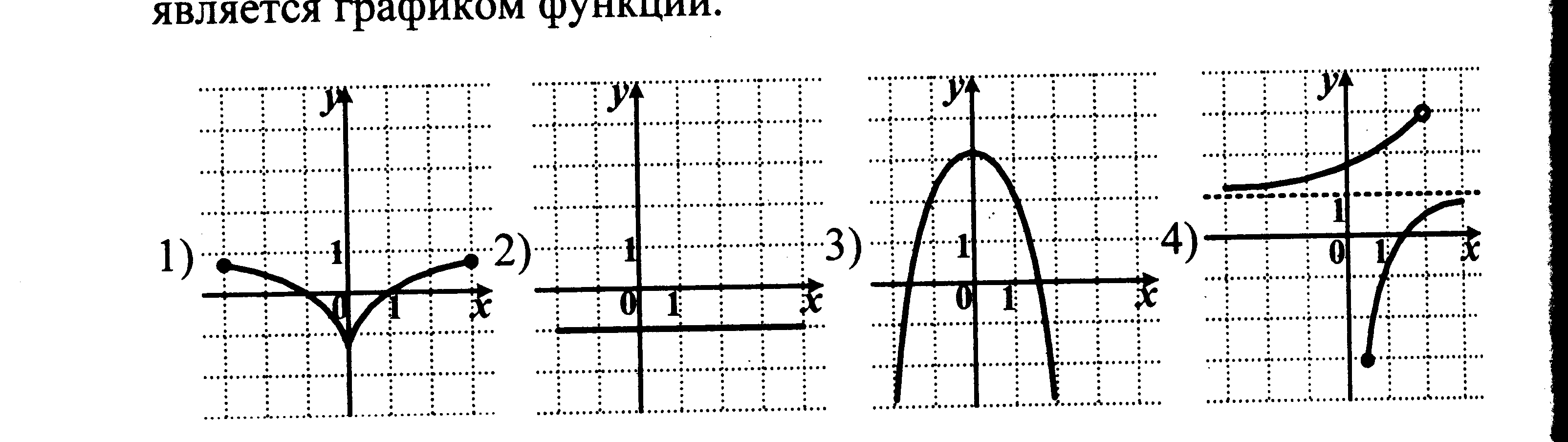
Ответ : а) 4; б) 3
№3. Найдите соответствия
|
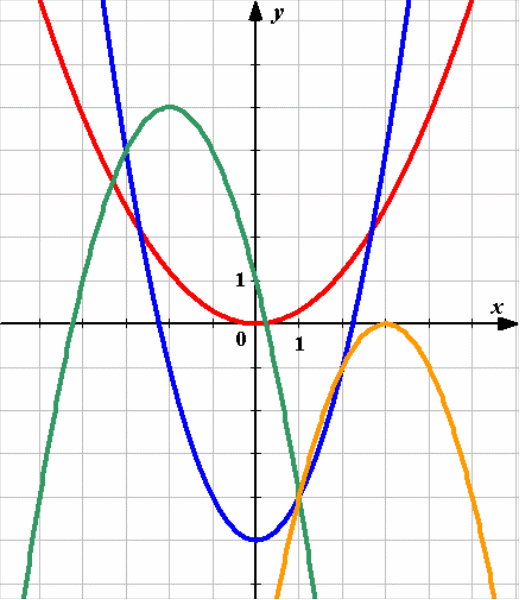
|
|
у = х2 – 5 |
у = 0,3х2 |
у = – (х – 3)2 |
у = – (х+ 2)2 +5
|
Ответ: 1 – синий, 2 – красный, 3 – жёлтый, 4 – зеленый
№4. На рисунке изображен график квадратичной функции. Какая из перечисленных формул задает эту функцию?
| 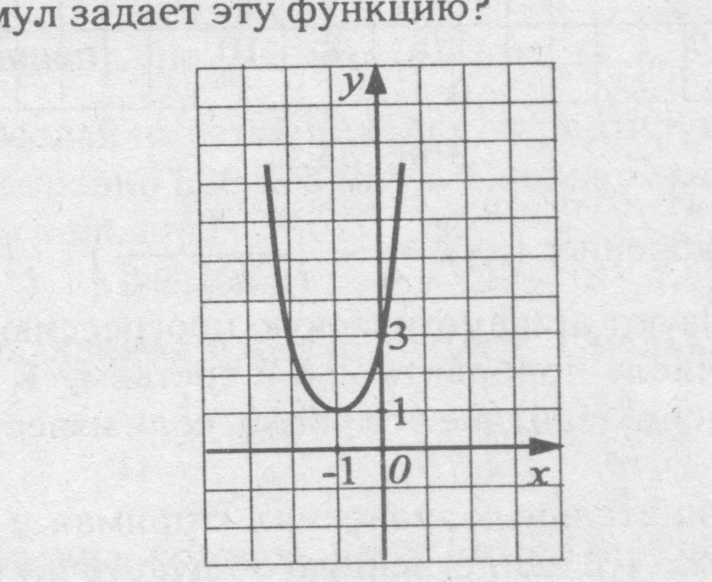
| у = – 2х2 +4х – 3 |
у = – 5х2 +10х + 3 |
у = х2 +2х + 3 |
у = 2х2 +4х + 3 |
|
|
Ответ: 4
Взаимопроверка. Учащиеся, работающие в тетради проверяют тех, которые работали у доски №341; 344(1,2).
III. Решение заданий из учебника(с проверкой)
Учитель. Открыли тетради, записали дату и тему урока.
Решаем №345(2). Один ученик на доске, остальные в тетради
IV. Физкультминутка
1. Повороты головы вправо- влево, вверх- вниз, показываем смещение вершины параболы
у = -х2+ 3 у = -(х – 2)2 у = -х2+ 6
у = х2- 5 у = (х + 1)2 у = -х2 – 8
2. Движения руками вверх- вниз, показываем направление ветвей параболы.
у = -х2+ 3 у = -(х – 2)2 у = -х2+ 6
у = х2- 5 у = (х + 1)2 у = -х2 – 8
V. Решение заданий из учебника(с проверкой)
Решаем №349. Один ученик на доске, остальные в тетради
VI. Контроль и коррекция знаний (карточки),
с последующей взаимопроверкой
| 1 вариант | 2 вариант |
| 1. График функции у = х2 + 4 получается из графика функции у =х2 сдвигом на 4 единицы: 1. Вправо. 2. Влево. 3. Вверх. 4. Вниз.
| 1. График функции у = х2 - 4 получается из графика функции у =х2 сдвигом на 4 единицы: 1. Вправо. 2. Влево. 3. Вверх. 4. Вниз.
|
| 2. График функции у = 2(х + 2)2 получается из графика функции у =2х2 сдвигом на 2 единицы: 1. Вправо. 2. Влево. 3. Вверх. 4. Вниз . | 2. График функции у = 2(х - 2)2 получается из графика функции у =2х2 сдвигом на 2 единицы: 1. Вправо. 2. Влево. 3. Вверх. 4. Вниз. |
| 3. Дана функция f(x) = 3x2 - 2x + 4. Найдите значение f(3) | 3. Дана функция f(x) = 2x2 + 3x - 6. Найдите значение f(2) |
| 4. Определите а) направление ветвей б) координаты вершины параболы у = х2 –6х – 7.
| 4. Определите а) направление ветвей б) координаты вершины параболы у = х2 +2х – 3.
|
| Номер задания | 1 | 2 | 3 | 4(а) | 4(б) |
| Вариант №___ |
|
|
|
|
|
Проверка теста
| Номер задания | 1 | 2 | 3 | 4(а) | 4(б) |
| Вариант №1 | 3 | 2 | 25 | вверх | (3; -16) |
| Вариант №2 | 4 | 1 | 8 | вверх | (-1; -4) |
VII. Информация о домашнем задании
Повторить материал п. 11, №346 (3,4), №350 из учебника . Вариант 17, задание 23(Типовые варианты экзаменационных заданий. Математика. ОГЭ. Под редакцией И. В. Ященко
VIII. Итог урока.
Дать оценку успешности достижения цели; самооценка учащимися реальных результатов изучения темы.
Объявляются оценки.
Рефлексия учебной деятельности
Продолжите предложения:
На уроке я научился…
Я получил полезную информацию о том, что…
Знания, полученные на уроке мне необходимы для…
Для меня сегодня было сложно…
Каждый для себя оценит свою работу на уроке. (Работал активно, пассивно, ленился…). Намете планы на следующий урок.
Спасибо за работу добросовестную и ответственную, спасибо за труд и умение,
такт и общение. Удачи в дальнейшем изучении математики