Урок математики в 5 классе "Сложение натуральных чисел; свойство нуля при сложении"

Математика, 5 класс на примере учебника «Математика. 5 класс», Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд А.Г.

Тема: Сложение натуральных чисел; свойство нуля при сложении.

Цели: формирование центральных математических понятий (число, величина);

подведение обучающихся к осознанию взаимосвязи математики и окружающего мира;

развитие интеллектуальных и творческих способностей обучающихся, критичности мышления, интереса к изучению математики;

формирование умения распознавать проявления зависимостей и закономерностей, формулировать их на языке математики и создавать математические модели, применять освоенный математический аппарат для решения практико-ориентированных задач.

Задачи: Исследовать свойства натурального ряда, чисел 0 и 1 при сложении.

Выполнять арифметические действия с натуральными числами, вычислять значения числовых выражений со скобками и без скобок. Выполнять прикидку и оценку значений числовых выражений, предлагать и применять приёмы проверки вычислений. Использовать при вычислениях переместительное и сочетательное свойства сложения, формулировать

и применять правила преобразования числовых выражений на основе свойств арифметических действий.

Планируемые результаты обучения:

а) ЛИЧНОСТНЫЕ РЕЗУЛЬТАТЫ

овладение языком математики и математической культурой как средством познания мира; овладение простейшими навыками исследовательской деятельности; готовность приобретать в совместной деятельности новые знания, навыки и компетенции из опыта других;

б) МЕТАПРЕДМЕТНЫЕ РЕЗУЛЬТАТЫ

1) Универсальные познавательные действия

выявлять и характеризовать существенные признаки математических объектов, понятий, отношений между понятиями; формулировать определения понятий; выявлять математические закономерности, взаимосвязи и противоречия в фактах, данных, наблюдениях и утверждениях; делать выводы с использованием законов логики, дедуктивных и индуктивных умозаключений, умозаключений по аналогии; использовать вопросы как исследовательский инструмент по-

знания; выбирать, анализировать, систематизировать и интерпретировать информацию различных видов и форм представления;

2) Универсальные коммуникативные действия

воспринимать и формулировать суждения в соответствии с условиями и целями общения; ясно, точно, грамотно выражать свою точку зрения в устных и письменных текстах, давать пояснения по ходу решения задачи, комментировать полученный результат; участвовать в групповых формах работы; владеть способами самопроверки, самоконтроля процесса и результата решения математической задачи;

в) ПРЕДМЕТНЫЕ РЕЗУЛЬТАТЫ

Понимать и правильно употреблять термины, связанные с натуральными числами; выполнять арифметические действия с натуральными числами, выполнять проверку, прикидку результата вычислений; решать задачи, содержащие зависимости, связывающие величины: скорость, время, расстояние; использовать краткие записи, таблицы, обозначения при решении задач; пользоваться основными единицами измерения: расстояния, времени, скорости.

Краткое учебное содержание.

Систематизация и развитие знаний о натуральных числах, полученных в начальной школе. Сложение натуральных чисел; свойство нуля при сложении. Использование при вычислениях переместительного и сочетательного свойств (законов) сложения. Решение текстовых задач арифметическим способом. Использование при решении задач таблиц и

схем.

Виды организации учебной деятельности.

индивидуальная работа;

фронтальная работа;

групповая форма работы.

Учебные задания для разных этапов учебного занятия.

Этапы урока:

1.Актуализация опорных знаний:

Сколько примеров и задач вы решили за 4 года обучения в школе?

Сколько раз вы писали «+» и «-», «*» и «/»?

А задумывались ли вы хоть раз о том, откуда эти знаки пришли и что означали?

(Найдите информацию по запросу: «История математических знаков»

Первое появление арифметических знаков + и – вместе в печатной книге зафиксировано в немецком трактате «Быстрый и приятный счет для всех торговцев», посвященном прикладной арифметике, который был написан Иоганном Видманом и опубликован в 1489 году, а знак минуса впервые появился чуть раньше – в рукописи по алгебре, написанной в 1481 и опубликованной в 1486 году. Современные символы сложения, вычитания, умножения, деления и равенства стандартны во всех странах мира. Они более универсальны, чем буквы любого письменного языка. Хотя их изображения просты и не поражают красотой, они надежно запечатлелись в нашем представлении о природе вещей.

Актуализация знаний;(фронтальный опрос)

Какое число надо прибавить к натуральному числу, чтобы получилось следующее за ним число? Ответ: Единицу.

Выполним устно номер №182.

999+1=1000

78099+1=78100

999999+1=1000000

А если нужно к 3+2, то (продолжить предложение) /к 3 прибавить 1 два раза/ получаем 3+1+1=5

Короче: 3+2=5

№183

76+24=100. Сколько единиц надо прибавить к числу 76, чтобы получить 100.

Ответ: 24

1.Как называют числа, которые складывают?

2. Как называют результат сложения?

3. Какое свойство сложения изображено на координатных лучах?

4. Какие законы (свойства) сложения вы изучили?

5. Если, а, в и с- натуральные числа, запишите переместительное, сочетательное свойство сложения.

6. Изменится ли число, если к нему прибавить 0?

7. Запишите свойство сложения с 0.

Устно: (Групповая работа на концентрацию внимания и быстроту мышления). Каждый выполняет 1 действие и результат передает следующему обучающемуся. Выигрывает та группа, которая быстрее и правильно выполнит действия.

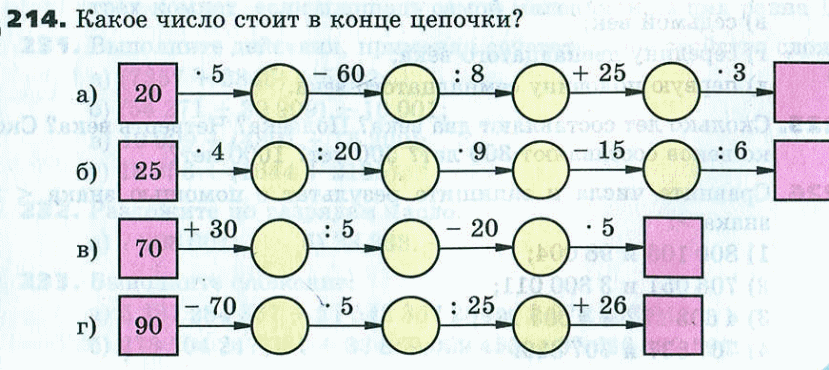
Откройте свои тетради, запишите в них число, классная работа и тему сегодняшнего урока.

Индивидуальная работа.

№191

Вычислить, выбирая удобный порядок действий.

а) (457+705) + 295 б) 554 + (46 + 1425)

Каким свойством мы здесь пользовались?

Работа в парах. (Обсуждение, составление плана, взаимоконтроль)

Физкультминутка

(Сменить деятельность, обеспечить эмоциональную разгрузку учащихся)

Мы работали отлично,

Отдохнуть не прочь сейчас,

И зарядка к нам привычно

На урок приходит в класс.

Выше руки, выше пятки,

Улыбнитесь веселей!

Мы попрыгаем, как зайки,

Сразу станем всех бодрей!

Потянулись и вдохнули.

Отдохнули? Отдохнули!

Самостоятельная работа «Экспресс-тест» «Сложение натуральных чисел».

(Контроль и коррекция знаний)

Вариант 1

1. Сумма 503 и 19 равняется:

А. 1083; Б. 522; В.921; Г.983

2) Вычислите удобным способом значение выражения; 38+263+37+262

3) В книге содержится два рассказа о животных. Первый, о гренландских китах, занимает на 11 страниц меньше, чем второй, об австралийских страусах. Если первый рассказ занимает 36страниц, то оба занимают:

А. 60стр. Б. 84стр. В.83стр. Г.63стр.

Вариант 2

1. Сумма 304 и 18 равняется:

А. 997; Б. 816; В. 322; Г.897.

2) Вычислите удобным способом значение выражения; 207+132+93+268

3) На стоянке находились под охраной автомобили «Форд» и «Лада». Автомобилей «Форд» было на 12 больше, чем «Лада». Сколько всего на стоянке автомобилей «Форд» и «Лада», если стояло 29 автомобилей «Форд»

А. 46машин; Б.71 машина; В.45машин; Г.70машин.

По завершению работы – самопроверка по образцу.

6. Итог урока: Самооценка результатов своей деятельности и всего класса

Домашнее задание: п.6 (правила), № 229, №231(а, б), № 232

Диагностические материалы для оценивания результатов обучения.

Тест по теме «Сложение натуральных чисел», 5 класс

1.Выберете верную запись переместительного свойства сложения для чисел 11 и 24.

А) 11+24=24-11

Б) 11+24=24*11

В) 11+24=24+11

Г) 11*24=24*11

2. Выберите неверное равенство

А) 16+0=16

Б) 0+32=0

В) 0+42=42

Г) 67-0=67

3. Нейдите значение суммы чисел 324 и 765

А) 1890

Б) 1089

В) 1998

Г) 989

4. Вычислите: 2314781+988428

А) 887760

Б) 3403199

В) 3303209

Г) 8887061

5. В первом ящике было 64 кг яблок, что на 24 кг больше, чем во втором ящике. Сколько килограммов яблок было в обоих ящиках вместе?

А) 152

Б) 88

В) 112

Г) 104

Вариант 2

1.Выберете верную запись сочетательного свойства сложения для чисел 54, 3 и 21.

А)54-(21+3) =54-21-3

Б) 21+(54-3) =(21+54) -3

В) 21+(3+54) =(21+3) +54

Г) 21*(54-3) =21*54-21*3

2. Выберите неверное равенство

А) 76+0=76

Б) 0+54=54

В) 0+22=0

Г) 167-0=167

3. Нейдите значение суммы чисел 926 и 765

А) 1681

Б) 1781

В) 16811

Г) 1691

4. Вычислите: 2414780+988428

А) 3403208

Б) 1426352

В) 3303209

Г) 2387068

5. В первом ящике было 64 кг яблок, что на 24 кг меньше, чем во втором ящике. Сколько килограммов яблок было в обоих ящиках вместе?

А) 152

Б) 88

В) 112

Г) 104

Ключ к тесту:

1 вариант: 1) -В, 2) -Б, 3) -Б, 4) -В, 5) -Г.

2 вариант: 1) -В, 2) -В, 3) -Г, 4) -А, 5) -А