Класс: 8 «А»
Учитель: Сенина Екатерина Владимировна
Тема: Преобразование выражений, содержащих квадратные корни.
Цели урока:
Обучающие:
обобщение и систематизация знаний учащихся по изученной теме;
ликвидация пробелов в знаниях и умениях учащихся
установление внутри предметных связей изученной темы с другими темами курса алгебры;
Развивающие:
Воспитательные:
воспитание чувства коллективизма, товарищества, ответственности за порученное дело,
воспитание воли, упорства в достижении поставленной цели.
Оборудование, наглядные пособия: учебник, таблицы, сигнальные карточки, раздаточный материал – карточки.
Тип урока: урок обобщения и систематизации
Метод урока: практический.
Ход урока
1.Организационный момент. 1 мин.
Сегодня на уроке мы будем повторять правила преобразования выражений, содержащих квадратные корни, закреплять преобразование корней из произведения, дроби , умножение и деление корней, вынесение множителя за знак корня, внесение множителя под знак корня, приведение подобных слагаемых .
Откройте тетради и запишите сегодняшнее число.
2.Мотивация урока. 5 мин.
Сегодня мы попытаемся почувствовать себя великими людьми, открывая знания для себя. Девиз сегодняшнего урока:
Приобретать знания – храбрость,
Приумножать их – мудрость,
А умело применять – великое искусство
Задача на внимание :
За каждый правильный ответ вы получаете по 1 балу.
(оформляем на листе таким образом, чтобы была видна всему классу; показываю и убираю, затем задаю вопросы, на которые ученики должны ответить по памяти).
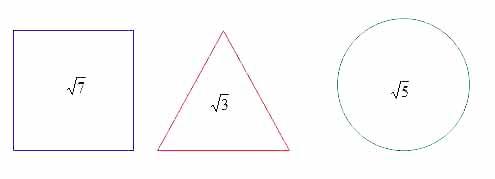
Вопросы:
Назовите все квадратные корни, которые вы запомнили.
Какого цвета был треугольник?
Квадратный корень из какого числа находится в окружности?
Какого цвета окружность?
Каков цвет фигуры, в которой стоял ?
?
В какой геометрической фигуре он расположен?
Расставьте все предложенные корни в порядке возрастания.
3.Актуализация опорных знаний. 7 мин.
-Блиц-опрос. Самопроверка.
За каждый правильный ответ вы получаете по 1 балу.

1. Квадратным корнем из числа а, называется число
____________________________________________________
2. Как называется знак  __ __________
__ __________  ______________________
______________________
3. Как называется выражение, стоящее под знаком корня____________________________________________________
4.Квадратный корень из произведения неотрицательных множителей равен
5. Квадратный корень из частного равен ____________________________________________________
4.Устный счёт. (работа с сигнальными карточками) 2 мин.
Учитель предлагает задания на доске,учащиеся показывают сигнальные карточки: зелёную – если ответ правильный и красную – если ответ неверный.˃




За каждый правильный ответ вы получаете по 1 балу.
5.Закрепление ЗУН учащихся. Выполнение задания по группам 15 мин.
1 группа. Консультант – Вакасова Дильназ
ПРИБЛИЖЕННЫЕ МЕТОДЫ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ
Около 3000 лет до нашей эры в Древнем Вавилоне пользовались формулой для приблеженного вычисления квадратного корня из числа. Если перевести эту формулу на современный язык алгебры, то она выглядит так:  ≈a +
≈a + 

2 группа. Консультант – Анищенко Валентин
Найди ошибку.
 =
= 
 =
=  -
-  = 6 – 5 = 1
= 6 – 5 = 1
 19
19
3 группа. Консультант – Сиренко Мария.
РАЗГАДАЙ МАТЕМАТИЧЕСКИЙ КРОССВОРД
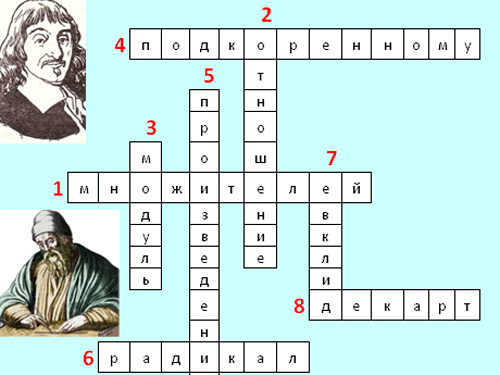
| 1) Корень из произведения- есть произведение корней из входящих в произведение …… |
|
|
|
|
|
| 2) Корень из дроби есть ….. корня из числителя к корню из знаменателя |
| 3) Квадратным корнем из выражения в квадрате является …. подкоренного выражени я |
| 4) Квадратный корень во второй степени равен … выражению |
| 5) Свойство, которое используется при вынесении множителя из-под знака корня, коротко называется "корень из …." 6) Как иногда называют знак арифметического квадратного корня? |
| 7) Древнегреческий математик, который доказал, что 2 не является рациональным числом |
| 8) Известный французский математик, в 1678 году впервые ввел современный знак радикала |
6.Физкультминутка 1 мин.
Все ребята Дружно встали, улыбнулись
Выше-выше потянулись.
Ну-ка, плечи распрямите,
Поднимите, опустите.
Вправо, влево повернитесь,
Рук коленями коснитесь.
Сели, встали. Сели, встали.
И на месте пошагали.
7. Обобщение и систематизация ЗУН учащихся. 5 мин.
Работа учащихся с учебником. Решить №152(1) №154(1,3)
№152(1)
2 двумя способами решают
двумя способами решают
№154
1) ( -
-  ) ·
) ·  =
=  ·
·  -
-  ·
·  =
=  -
-  = 10 – 5 = 5
= 10 – 5 = 5
3) ( - 2)(
- 2)( + 2) =(
+ 2) =( )² - 2² =
)² - 2² =  - 4 = 7 – 4 =3
- 4 = 7 – 4 =3
8. Самостоятельная работа. Выполнение тестового задания. 6 мин.
Взаимопроверка внутри группы.
За каждый правильный ответ вы получаете по 1 балу.
Тест:
Найти значение выражения:  -2
-2
А. 9,6 Б. 0 В. 10 Г. 2,4
Вычислите: (2  )2 + 1
)2 + 1
А. 25 Б. 18 В. 60 Г. 6
Найти значение выражения: 5 + 3
+ 3
А. 0 Б. 62,93 В. 1 Г.28
 4. Найти значение выражения:
4. Найти значение выражения:
А. 141 Б. -2 В. 2
В. 2 Г. 0
Г. 0
5. Вычислите значение выражения: 
А. 0,1 Б. 0,7 В.1 Г.0
9. Подведение итогов урока. Д/з. 2 мин.
За каждый правильный ответ вы получаете по 1 балу.
1. Какое число называется квадратным корнем из числа?
2. Как называется действие нахождения квадратного корня?
3. Как называется выражение, стоящее под знаком корня?
4. Каким должно быть число, чтоб можно было извлечь квадратный корень?
5. Какое число называется арифметическим квадратным корнем?
Откройте дневники, записываем домашнее задание №152(2) №154(2,4)
10. Рефлексия. 1 мин.
ЛИСТ-ОТВЕТОВ
Ф.И. ученика____________________________



1. Настроение в начале урока: а) б) в)
2. Мое восприятие урока:
а) усвоил(а) все; б) усвоил(а) почти все; в) усвоил(а) частично, нуждаюсь в помощи.
3. Я работал(а) на уроке:
а) отлично; б) хорошо; в) удовлетворительно; г) неудовлетворительно.
4. Я оцениваю урок на _____ (поставьте оценку)

5. Полученные балы в течении урок:
Общая сумма балов за урок:




6. Настроение в конце урока: а) б в)








 __ __________
__ __________  ≈a +
≈a + 

 =
= 
 =
=  -
-  = 6 – 5 = 1
= 6 – 5 = 1 19
19
 двумя способами решают
двумя способами решают -
- 









