Урок по алгебре, 8 класс

Алгебра 8 класс Дата: 11.09.2020

Урок № 5(1)

Тема: Рациональные дроби

Тема урока: Рациональные дроби и их свойства. Рациональные выражения

Образовательная цель: ввести понятия, какие выражения называют целыми и дробными. Познакомимся с рациональными выражениями. Узнаем, какие значения называют допустимыми. А также научимся находить допустимые значения выражения.

Развивающая цель: память, логическое мышление, активизация мыслительной деятельности.

Воспитательная цель: самостоятельность, дисциплинированность, точность и аккуратность ведения математической записи.

Тип урока. Комбинированный.

Метод. Словесный, беседа, рассказ.

Литература / основная/ Алгебраа. 8 класс: учеб. для общеобразоват. организаций/ .—5-е изд.- М. : Просвещение, 2016.

Оборудование: мел, доска

Дидактический , раздаточный материал.

Ход урока

1. Организационный момент. Мотивация (самоопределение) к учебной

Проверка посещаемости

1. Актуализация, пробное учебное действие. На этом уроке мы вспомним, какие выражения называют целыми и дробными. Познакомимся с рациональными выражениями. Узнаем, какие значения называют допустимыми. А также научимся находить допустимые значения выражения.

2. Сформулируйте тему и цель урока.

3. Формирование умений и навыков.

Вы уже знакомы с целыми и дробными выражениями. Вспомним их определения.

Целые выражения – это выражения, составленные из чисел и переменных, содержащие действия сложения, вычитания и умножения, а также деления на число, отличное от нуля.

Например

В отличие от целых выражений, дробные выражения помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными.

Например

Целые и дробные выражения называют рациональными выражениями.

Определение

Рациональными выражениями называют выражения, составленные из чисел, переменных, их степеней и знаков арифметических действий.

Например

Напомним, что целые выражения имеют смысл при любых значениях переменных. Чтобы найти значение целого выражения, нужно подставить указанное значение переменной и выполнить все действия.

Дробное выражение при некоторых значениях переменных может не иметь смысла.

Например

Чтобы найти значение рационального выражения, надо:

1)    подставить числовое значение переменной в данное выражение;

2)    выполнить все действия.

Определение : Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.

Множество всех допустимых значений переменных называется областью допустимых значений (коротко ОДЗ) или областью определения выражения.

Как вы уже знаете, выражение вида   называется дробью.

Дробь, числитель и знаменатель которой многочлены, называют рациональной дробью.

Например

Задание

Найдите значение дроби.

         

Задание

Найдите допустимые значения переменной в выражениях:

         

Рефлексия учебной деятельности на уроке. Подведение итогов урока.

Целые выражения – это выражения, составленные из чисел и переменных, содержащие действия сложения, вычитания и умножения, а также деления на число, отличное от нуля.

В отличие от целых выражений, дробные выражения помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными.

Рациональными выражениями называют выражения, составленные из чисел, переменных, их степеней и знаков арифметических действий.

Чтобы найти значение рационального выражения, надо:

1)    Подставить числовое значение переменной в данное выражение;

Анализ работы в классе. Какая была цель? Справились?

6.Оценивание.

7. Домашнее задание. Учитель пишет на доске.

Алгебра 8 класс Дата: 14.09.2020

Урок № 6 (2)

Тема: Рациональные дроби и их свойства. Основное свойство дроби. Сокращение дробей

Образовательная цель: закрепить, какие выражения называют целыми и дробными. Познакомимся с основным свойством рациональной дроби. Сформируем представления о тождествах, тождественно равных выражениях и тождественных преобразованиях. с рациональными выражениями.

Развивающая цель: память, логическое мышление, активизация мыслительной деятельности.

Воспитательная цель: самостоятельность, дисциплинированность, точность и аккуратность ведения математической записи.

Тип урока. Комбинированный.

Метод. Словесный, беседа ,рассказ.

Литература / основная/ Алгебраа. 8 класс: учеб. для общеобразоват. организаций/ .—5-е изд.- М. : Просвещение, 2016.

Оборудование : мел , доска

Дидактический , раздаточный материал.

Ход урока

1. Организационный момент.

Проверка посещаемости;

Проверка домашнего задания

1. Актуализация базовых знаний

1. какие выражения называют целыми и дробными.

2. какие выражения называют рациональными выражениями.

3. какие значения называют допустимыми;

4. как находить допустимые значения выражения.

1. Сформулируйте тему и цель урока.

На этом уроке мы узнаем основное свойство рациональной дроби. Сформируем представления о тождествах, тождественно равных выражениях и тождественных преобразованиях. А также выполним задания на сокращение и приведение рациональных дробей к общему знаменателю.

1. Формирование умений и навыков  

Вы уже знакомы с основным свойством дроби. Давайте вспомним его:

Если числитель и знаменатель дроби умножить или разделить на одно и то же число, отличное от нуля, то значение дроби не изменится.

Иначе говоря, при любых a, b и c верны равенства

Хотелось бы сразу уточнить, что деление числителя и знаменателя на одно и то же число называется сокращением дроби.

Равенство,   справедливо и не только при натуральных, но и при любых значениях переменных a, b и c при которых знаменатель не равен нулю.

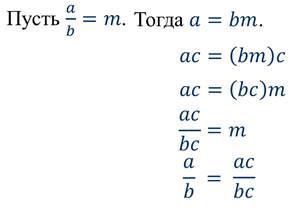
Рациональные дроби  тоже можно преобразовывать таким же образом.

Рациональная дробь – это дробь, числитель и знаменатель которой многочлены.

Основное свойство рациональной дроби сводится к тому, что:

Если числитель и знаменатель рациональной дроби умножить на один и тот же ненулевой многочлен, то получится равная ей дробь.

Если числитель и знаменатель рациональной дроби разделить на один и тот же ненулевой многочлен, то получится равная ей дробь.

Например

 

Это равенство верно при всех допустимых значениях переменной. Такие равенства называют тождествами.

Определение:

Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных.

Два выражения, принимающие равные значения при всех допустимых значениях переменных, называются тождественно равными.

Замену одного такого выражения другим называют тождественным преобразованием выражения.

Равенство

Основное свойство рациональной дроби позволяет сокращать дроби и приводить дробь к новому знаменателю.

Чтобы сократить рациональную дробь, нужно предварительно разложить на множители числитель и знаменатель дроби, а затем разделить их на общие множители.

Задание

Сократить дробь.

Решение:

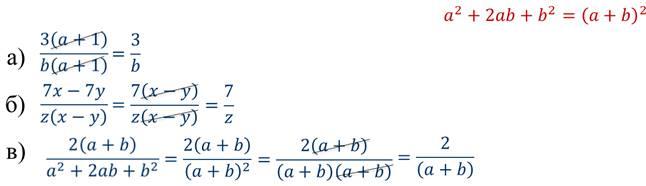
Задание

Привести дробь к указанному знаменателю.

Решение:

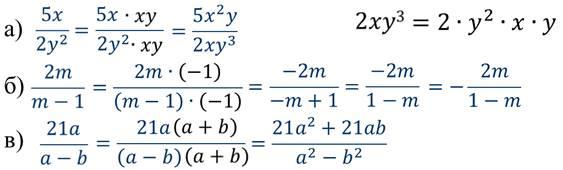
1. Рефлексия учебной деятельности на уроке. Подведение итогов урока.

Если числитель и знаменатель рациональной дроби умножить на один и тот же ненулевой многочлен, то получится равная ей дробь.

Если числитель и знаменатель рациональной дроби разделить на один и тот же ненулевой многочлен, то получится равная ей дробь.

Основное свойство рациональной дроби позволяет сокращать дроби и приводить дробь к новому знаменателю.

6.Оценивание.

7. Домашнее задание. Учитель пишет на доске.

Алгебра 8 класс Дата:15.09.2020

Урок № 7 (3)

Тема: Рациональные дроби и их свойства. Сокращение дробей

Образовательная цель: закрепить основным свойства рациональных дробей и тождественные преобразования с рациональными выражениями.

Развивающая цель: память, логическое мышление, активизация мыслительной деятельности.

Воспитательная цель: самостоятельность, дисциплинированность, точность и аккуратность ведения математической записи.

Тип урока. Комбинированный.

Метод. Словесный, беседа, рассказ.

Литература / основная/ Алгебра. 8 класс: учеб. для общеобразоват. организаций/ .—5-е изд.- М. : Просвещение, 2016.

Оборудование : мел , доска

Дидактический , раздаточный материал.

Ход урока

1. Организационный момент.

Проверка посещаемости;

Проверка домашнего задания

2.Актуализация базовых знаний

1. ) какие выражения называют целыми и дробными.

2. ) какие выражения называют рациональными выражениями.

3 )Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных.

1. ) какие выражения называют тождественно равными ?

Два выражения, принимающие равные значения при всех допустимых значениях переменных, называются  тождественно равными.

3. Мотивация учебной деятельности ,тема и цель урока.

Закрепить основное свойство рациональной дроби, представления о тождествах, тождественно равных выражениях и тождественных преобразованиях. выполнить задания на сокращение и приведение рациональных дробей к общему знаменателю.

1. Формирование умений и навыков  

Вы уже знакомы с основным свойством дроби. Давайте вспомним его:

Если числитель и знаменатель дроби умножить или разделить на одно и то же число, отличное от нуля, то значение дроби не изменится.

Иначе говоря, при любых a, b и c верны равенства

Хотелось бы сразу уточнить, что деление числителя и знаменателя на одно и то же число называется сокращением дроби.

Равенство,   справедливо и не только при натуральных, но и при любых значениях переменных a, b и c при которых знаменатель не равен нулю.

Рациональные дроби  тоже можно преобразовывать таким же образом.

Рациональная дробь – это дробь, числитель и знаменатель которой многочлены.

Основное свойство рациональной дроби сводится к тому, что:

Если числитель и знаменатель рациональной дроби умножить на один и тот же ненулевой многочлен, то получится равная ей дробь.

Если числитель и знаменатель рациональной дроби разделить на один и тот же ненулевой многочлен, то получится равная ей дробь.

Например

 

Это равенство верно при всех допустимых значениях переменной. Такие равенства называют тождествами.

Определение:

Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных.

Два выражения, принимающие равные значения при всех допустимых значениях переменных, называются тождественно равными.

Замену одного такого выражения другим называют тождественным преобразованием выражения.

свойство рациональной дроби позволяет сокращать дроби и приводить дробь к новому знаменателю.

Чтобы сократить рациональную дробь, нужно предварительно разложить на множители числитель и знаменатель дроби, а затем разделить их на общие множители.

Задание

Сократить дробь.

Привести дробь к указанному знаменателю.

Решение: №№

1. Рефлексия учебной деятельности на уроке. Подведение итогов урока.

6.Оценивание.

7. Домашнее задание. Учитель пишет на доске.

Алгебра 8 класс Дата : 18.09.2020

Урок № 8(4)

Тема: Рациональные дроби и их свойства. Сокращение дробей. Решение упражнений.

Образовательная цель: закрепить основным свойства рациональных дробей и тождественные преобразования с рациональными выражениями.

Развивающая цель: память, логическое мышление, активизация мыслительной деятельности.

Воспитательная цель: самостоятельность, дисциплинированность, точность и аккуратность ведения математической записи.

Тип урока. Комбинированный.

Метод. Словесный, беседа ,рассказ.

Литература / основная/ Алгебраа. 8 класс: учеб. для общеобразоват. организаций/ .—5-е изд.- М. : Просвещение, 2016.

Оборудование : мел , доска

Дидактический , раздаточный материал.

Ход урока

1. .Организационный момент.

Проверка посещаемости;

Проверка домашнего задания

2.Актуализация базовых знаний

1) какие выражения называют целыми и дробными.

2) какие выражения называют рациональными выражениями.

3 ) что называется тождеством ?

Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных.

4) какие выражения называют тождественно равными ?

Два выражения, принимающие равные значения при всех допустимых значениях переменных, называются  тождественно равными.

3. Мотивация учебной деятельности ,тема и цель урока.

Закрепить основное свойство рациональной дроби, представления о тождествах, тождественно равных выражениях и тождественных преобразованиях. выполнить задания на сокращение и приведение рациональных дробей к общему знаменателю.

4.Формирование умений и навыков  

Что является основным свойством дроби.

Если числитель и знаменатель дроби умножить или разделить на одно и то же число, отличное от нуля, то значение дроби не изменится.

Иначе говоря, при любых a, b и c верны равенства

Хотелось бы сразу уточнить, что деление числителя и знаменателя на одно и то же число называется сокращением дроби.

Равенство,   справедливо и не только при натуральных, но и при любых значениях переменных a, b и c при которых знаменатель не равен нулю.

Рациональные дроби  тоже можно преобразовывать таким же образом.

Рациональная дробь – это дробь, числитель и знаменатель которой многочлены.

Основное свойство рациональной дроби сводится к тому, что:

Если числитель и знаменатель рациональной дроби умножить на один и тот же ненулевой многочлен, то получится равная ей дробь.

Если , числитель и знаменатель рациональной дроби разделить на один и тот же ненулевой многочлен, то получится равная ей дробь. 

Если , равенство верно при всех допустимых значениях переменной. Такие равенства называют тождествами.

Определение:

Тождеством называется равенство, верное при всех допустимых значениях входящих в него переменных.

Два выражения, принимающие равные значения при всех допустимых значениях переменных, называются тождественно равными.

Замену одного такого выражения другим называют тождественным преобразованием выражения.

свойство рациональной дроби позволяет сокращать дроби и приводить дробь к новому знаменателю.

Чтобы сократить рациональную дробь, нужно предварительно разложить на множители числитель и знаменатель дроби, а затем разделить их на общие множители.

Задание на доске

Сократить дробь.

Привести дробь к указанному знаменателю.

Решение в классе №№

1. Рефлексия учебной деятельности на уроке. Подведение итогов урока.

6.Оценивание.

7. Домашнее задание. Учитель пишет на доске.

Алгебра 8 класс Дата: 21.09.2020

Урок № 9(5)

Тема: Сложение и вычитание дробей с одинаковыми знаменателями

Образовательная цель: рассмотреть теоретические аспекты сложение и вычитание дробей ; закрепить представления о рациональных выражениях; формировать представления о преобразовании рациональных выражений. Ввести правило сложения и вычитания рациональных дробей с одинаковыми знаменателями.

Развивающая цель: память, логическое мышление, активизация мыслительной деятельности.

Воспитательная цель: самостоятельность, дисциплинированность, точность и аккуратность ведения математической записи.

Тип урока. Комбинированный.

Метод. Словесный, беседа ,рассказ.

Литература / основная/ Алгебраа. 8 класс: учеб. для общеобразоват. организаций/ .—5-е изд.- М. : Просвещение, 2016.

Оборудование : мел, доска

Дидактический раздаточный материал:

Ход урока

1.Организационный момент.

Проверка посещаемости;

Проверка домашнего задания

2.Актуализация базовых знаний

1) Дайте определение основного свойства дроби.

2) Как сократить рациональную дробь?

3) Что означает выражение « выполнить тождественное преобразование»?

3. Мотивация учебной деятельности ,тема и цель урока.

Вы умеете складывать и вычитать обыкновенные дроби с одинаковыми знаменателям, вспомним правила, по которым складывают и вычитают обыкновенные дроби.

4.Формирование умений и навыков 

 Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тем же.

Чтобы из одной дроби вычесть другую дробь с таким же знаменателем, нужно из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тем же.

В буквенном виде эти правила можно записать так:   

Например

Эти равенства являются тождествами, т.к. они верны при любых значениях переменных a, b и c, кроме цэ равного нулю.

Доказательство:

Таким образом, складывают любые рациональные дроби с одинаковыми знаменателями.

Правило сложения рациональных дробей с одинаковыми знаменателями:

Чтобы сложить рациональные дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тем же.

В буквенном виде это правило можно записать так:

Это правило справедливо при сложении любого числа дробей.

Пример1. из учебника стр. 18. Сложим дроби

= = = =

Пример на закрепление. Найти сумму дробей.

Решение:

Пример 2. из учебника стр. 18. Вычтем из дроби дробь

.

Пример на закрепление. Найти сумму дробей.

Решение:

Пример3. Упростить выражение

= = = =

Работа учащихся у доски. Решение заданий на повторение № 70 а),б).

Задание на доске

Решение в классе №№ 53 а);б), 54 а);б), 55а);б), 56 а);б),

Рефлексия учебной деятельности на уроке. Подведение итогов урока.

6.Оценивание. Выставление оценок в дневники.

7. Домашнее задание. Учитель пишет на доске. Пункт 3. Стр.17-21.№№ 53в);г), 54в);г), 55в);г), 56г);д),е).

Алгебра 8 класс Дата: 22.09.2020

Урок № 10(6)

Тема: Сложение и вычитание дробей с разными знаменателями

Образовательная цель: рассмотреть теоретические аспекты сложение и вычитание дробей с разными знаменателями ;закрепить представления о рациональных выражениях; формировать представления о преобразовании рациональных выражений. Ввести правило сложения и вычитания рациональных дробей с разными знаменателями.

Развивающая цель: память, логическое мышление, активизация мыслительной деятельности.

Воспитательная цель: самостоятельность, дисциплинированность, точность и аккуратность ведения математической записи.

Тип урока. Комбинированный.

Метод. Словесный, беседа,рассказ.

Литература / основная/ Алгебраа. 8 класс: учеб. для общеобразоват. организаций/ .—5-е изд.- М. : Просвещение, 2016.

Оборудование: мел, доска,тряпка

Дидактический раздаточный материал.

Ход урока

1.Организационный момент.

Проверка посещаемости;

Проверка домашнего задания №№ 53в);г), 54в);г), 55в);г), 56г), д),е).

2.Актуализация базовых знаний. Фронтально индивидуальная беседа.

1) Чтобы сложить дроби с одинаковыми знаменателями, нужно …

2) Чтобы из одной дроби вычесть другую дробь с таким же знаменателем, нужно из числителя уменьшаемого вычесть числитель….

3 ) В буквенном виде эти правила можно записать так:   

3. Мотивация учебной деятельности ,тема и цель урока.

Вы умеете складывать и вычитать обыкновенные дроби с одинаковыми знаменателям, вспомним правила, по которым складывают и вычитают дроби с разными знаменателями.

4.Формирование умений и навыков

 Пример 3. Найти сумму дробей. Продолжаем закреплять умения на решение рациональных дробей с одинаковыми знаменателями.

Решение:

Вычитание рациональных дробей с одинаковыми знаменателями выполняется аналогично сложению.

Правило вычитания рациональных дробей с одинаковыми знаменателями

Чтобы выполнить вычитание рациональных дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тем же.

В буквенном виде это правило можно записать так:

Пример 4. Найти разность дробей.

Решение:

Пример 5. Найти разность дробей.

Решение:

Пример 6. Выполнить действия.

Решение:

Решение в классе №№ 57а),в),д), 59а), 61а), в), д), 62 а),б), 65.

Рефлексия учебной деятельности на уроке. Подведение итогов урока.

Чтобы сложить рациональные дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тем же.

Чтобы выполнить вычитание рациональных дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тем же.

6.Оценивание.Анализ работы в классе. Выставление оценок в дневники.

7. Домашнее задание. Учитель пишет на доске. №№ 57 б),г),е), №59б), №61б), г), е), №62 в),г),д),е). №64.

Алгебра 8 класс Дата : 25.09.2020

Урок № 11(7)

Тема: Сложение и вычитание дробей с разными знаменателями

Образовательная цель: рассмотреть теоретические аспекты сложение и вычитание дробей ,закрепить представления о рациональных выражениях; формировать представления о преобразовании рациональных выражений. Ввести правило сложения и вычитания рациональных дробей с разными знаменателями.

Развивающая цель: память, логическое мышление, активизация мыслительной деятельности.

Воспитательная цель: самостоятельность, дисциплинированность, точность и аккуратность ведения математической записи.

Тип урока. Комбинированный.

Метод. Словесный, беседа ,рассказ.

Литература / основная/ Алгебра. 8 класс: учеб. для общеобразоват. организаций/ .—5-е изд.- М. : Просвещение, 2016.

Оборудование : мел, доска

Дидактический , раздаточный материал.

Ход урока

1.Организационный момент.

Проверка посещаемости;

Проверка домашнего задания

2.Актуализация базовых знаний

1) Чтобы сложить дроби с одинаковыми знаменателями, нужно …

2) Чтобы из одной дроби вычесть другую дробь с таким же знаменателем, нужно из числителя уменьшаемого вычесть числитель….

3 ) В буквенном виде эти правила можно записать так:   

3. Мотивация учебной деятельности ,тема и цель урока.

Вы умеете складывать и вычитать обыкновенные дроби с одинаковыми знаменателям, вспомним правила, по которым складывают и вычитают дроби с разными знаменателями.

4.Формирование умений и навыков

Сложение и вычитание рациональных дробей с разными знаменателями выполняется аналогично сложению и вычитанию дробей с одинаковыми знаменателями, но предварительно нужно дроби привести к общему знаменателю.

Например:

Аналогичным образом выполняют вычитание рациональных дробей с разными знаменателями.

Пример Найти сумму дробей.

Решение:

Пример1. из учебника стр. 22. Сложим дроби

= =

Пример 2. Найти разность дробей.

Решение:

Решение в классе №№ 73а),б);74 в),75 б),76 в),77 б)

Рефлексия учебной деятельности на уроке. Подведение итогов урока.

1.     Разложить знаменатели каждой из дробей на множители.

2.     Найти общий знаменатель дробей.

3.     Для каждой из дробей найти дополнительный множитель.

4.     Числитель дроби умножить на её дополнительный множитель.

5.     Записать каждую дробь с числителем и общим знаменателем.

6.Оценивание.

7. Домашнее задание. Учитель пишет на доске.

Алгебра 8 класс Дата : 28.09.2020

Урок № 12(8)

Тема: Решение упражнений .Сложение и вычитание дробей с разными знаменателями

Образовательная цель: закрепить представления о рациональных выражениях; формировать представления о преобразовании рациональных выражений. Закрепить умения и навыки сложения и вычитания рациональных дробей с разными знаменателями.

Развивающая цель: память, логическое мышление, активизация мыслительной деятельности.

Воспитательная цель: самостоятельность, дисциплинированность, точность и аккуратность ведения математической записи.

Тип урока. Урок формирования умений и навыков.

Метод. Словесный, беседа ,рассказ.

Литература / основная/ Алгебраа. 8 класс: учеб. для общеобразоват. организаций/ .—5-е изд.- М. : Просвещение, 2016.

Оборудование : мел , доска

Дидактический , раздаточный материал.

Ход урока

1.Организационный момент.

Проверка посещаемости;

Проверка домашнего задания

2.Актуализация базовых знаний

1) Чтобы сложить дроби с одинаковыми знаменателями, нужно …

2) Чтобы из одной дроби вычесть другую дробь с таким же знаменателем, нужно из числителя уменьшаемого вычесть числитель….

3 ) В буквенном виде эти правила можно записать так:   

3. Мотивация учебной деятельности ,тема и цель урока.

Вы умеете складывать и вычитать обыкновенные дроби с одинаковыми знаменателям, вспомним правила, по которым складывают и вычитают дроби с разными знаменателями.

4.Формирование умений и навыков

Например:

Аналогичным образом выполняют вычитание рациональных дробей с разными знаменателями.

Пример 3. Найти сумму дробей.

Решение:

Пример 4: Найдите разность дробей.

Решение:

Алгоритм сложения (вычитания) рациональных дробей с разными знаменателями.

Для того чтобы сложить (вычесть) дроби с разными знаменателями, надо:

1.     Найти общий знаменатель дробей.

2.     Привести дроби к общему знаменателю.

3.     Сложить (вычесть) дроби по правилу сложения (вычитания) рациональных дробей с одинаковыми знаменателями.

4.     По возможности упростить полученную дробь.

Решение в классе №№

Рефлексия учебной деятельности на уроке. Подведение итогов урока.

Алгоритм сложения (вычитания) рациональных дробей с разными знаменателями.

Для того чтобы сложить (вычесть) дроби с разными знаменателями, надо:

-   Найти общий знаменатель дробей.

-    Привести дроби к общему знаменателю.

-   Сложить (вычесть) дроби по правилу сложения (вычитания) рациональных дробей с одинаковыми знаменателями.

- По возможности упростить полученную дробь.

6.Оценивание.

7. Домашнее задание. Учитель пишет на доске.

Алгебра 8 класс Дата : 29.09.2019

Урок № 13(9)

Тема: Решение упражнений .Сложение и вычитание дробей с разными знаменателями

Образовательная цель: рассмотреть теоретические аспекты сложение и вычитание дробей ;закрепить представления о рациональных выражениях; формировать представления о преобразовании рациональных выражений. Закрепить правило сложения и вычитания рациональных дробей с разными знаменателями.

Развивающая цель: память, логическое мышление, активизация мыслительной деятельности.

Воспитательная цель: самостоятельность, дисциплинированность, точность и аккуратность ведения математической записи.

Тип урока .Урок формирования умений и навыков.

Метод. Словесный, беседа ,рассказ.

Литература / основная/ Алгебраа. 8 класс: учеб. для общеобразоват. организаций/ .—5-е изд.- М. : Просвещение, 2016.

Оборудование : мел , доска

Дидактический , раздаточный материал.

Ход урока

1.Организационный момент.

Проверка посещаемости;

Проверка домашнего задания

2.Актуализация базовых знаний

1) Чтобы сложить дроби с одинаковыми знаменателями, нужно …

2) Чтобы из одной дроби вычесть другую дробь с таким же знаменателем, нужно из числителя уменьшаемого вычесть числитель….

3 ) В буквенном виде эти правила можно записать так:   

3. Мотивация учебной деятельности ,тема и цель урока.

Вспомним правила, по которым складывают и вычитают дроби с разными знаменателями и будем использовать эти знания на преобразованиях в дробно рациональных выражениях.

Пример .Упростить выражение

а - 1 - = = =

4.Формирование умений и навыков

Сложение и вычитание рациональных дробей с разными знаменателями выполняется аналогично сложению и вычитанию дробей с одинаковыми знаменателями, но предварительно нужно дроби привести к общему знаменателю.

Аналогичным образом выполняют вычитание рациональных дробей с разными знаменателями.

Пример 1. Найти сумму дробей и

Решение:

Общим знаменателем является одночлен 12 . Дополнительными множителями к числителям и знаменателям этих дробей 3 и 2 .

Имеем

+ = =

Пример 2. Найти разность дробей.

Решение:

= .

Дополнительными множителями есть а и в.

Имеем = =

Решение в классе №№ 73д)е),74а)б),75а),76 г),д),е);77))78)),79())

Рефлексия учебной деятельности на уроке. Подведение итогов урока.

Запомните:

1.     Разложить знаменатели каждой из дробей на множители.

2.     Найти общий знаменатель дробей.

3.     Для каждой из дробей найти дополнительный множитель.

4.     Числитель дроби умножить на её дополнительный множитель.

5.     Записать каждую дробь с числителем и общим знаменателем.

6.Оценивание.

7. Домашнее задание. Учитель пишет на доске.

Алгебра 8 класс Дата: 02.10.2020

Урок № 14(10)

Тема: Контрольная работа. Сложение и вычитание дробей с разными знаменателями

Образовательная цель: контроль по теме сложение и вычитание дробей ; преобразовании рациональных выражений ; сложения и вычитания рациональных дробей с разными знаменателями.

Развивающая цель: память, логическое мышление, активизация мыслительной деятельности.

Воспитательная цель: самостоятельность, дисциплинированность, точность и аккуратность ведения математической записи.

Тип урока. Урок контроля знаний.

Метод. Практический

Литература / основная/ Алгебраа. 8 класс: учеб. для общеобразоват. организаций/ .—5-е изд.- М. : Просвещение, 2016.

Оборудование : мел , доска

Дидактический , раздаточный материал.

Ход урока

1.Организационный момент.

Проверка посещаемости;

Проверка домашнего задания

Контрольная работа на два варианта

3. Мотивация учебной деятельности ,тема и цель урока.

4.Проверка умений и навыков

Рефлексия учебной деятельности на уроке. Подведение итогов урока.

6.Оценивание.

7. Домашнее задание. Учитель пишет на доске.

Алгебра 8 класс Дата: 05.10.2020

Урок № 15(11)

Тема: Анализ контрольной работы . Произведение дробей

Образовательная цель: Провести анализ контрольной работы; рассмотреть теоретические аспекты произведения дробей ;закрепить представления о рациональных выражениях; формировать представления о преобразовании рациональных выражений.

Развивающая цель: память, логическое мышление, активизация мыслительной деятельности.

Воспитательная цель: самостоятельность, дисциплинированность, точность и аккуратность ведения математической записи.

Тип урока .Урок формирования умений и навыков.

Метод. Словесный, беседа ,рассказ.

Литература / основная/ Алгебра. 8 класс: учеб. для общеобразоват. организаций/ .—5-е изд.- М. : Просвещение, 2016.

Оборудование : мел , доска

Дидактический , раздаточный материал.

Ход урока

1.Организационный момент.

Проверка посещаемости;

Проверка домашнего задания

Анализ контрольной работы

2. Мотивация учебной деятельности ,тема и цель урока.

Вы умеете умножать обыкновенные дроби ,закрепим представления о рациональных выражениях. Введем правило умножения и возведения рациональных дробей в степень.

3.Формирование умений и навыков вспомним правило умножения обыкновенных дробей.          

Для того чтобы умножить дробь на дробь, надо числитель умножить на числитель, а знаменатель на знаменатель и первое произведение записать в числителе новой дроби, второе – в знаменателе.

Например

Аналогичным образом происходит умножение рациональных дробей. Давайте докажем, что это правило на самом деле действует при умножении рациональных дробей.

Иначе говоря, докажем, что произведение двух рациональных дробей тождественно равно дроби, у которой числитель равен произведению числителей, а знаменатель – произведению знаменателей перемножаемых дробей при любых допустимых значениях переменных, кроме b равное нулю и d равное нулю.

Получили, что равенство верно при любых допустимых значениях переменных, т.е. является тождеством.

Правило умножения рациональных дробей:

Чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе – знаменателем дроби.

В буквенном виде это правило записывают так:  

Это правило выполняется и когда произведение трёх и более рациональных дробей.

Прежде чем выполнять умножение рациональных дробей, полезно их числители и знаменатели разложить на множители. Это облегчит сокращение той рациональной дроби, которая получится в результате умножения.

Пример 1: умножить дроби.

Решение:

Пример 2: умножить дроби.

Решение:

Пример 3: Представить произведение дробей в виде рациональной дроби.

Решение:

Пример 4: выполнить умножение.

Решение:

Теперь

Решение в классе №№

Рефлексия учебной деятельности на уроке. Подведение итогов урока.

6.Оценивание.

7. Домашнее задание. Учитель пишет на доске.

  

Алгебра 8 класс Дата: 06.10.2020

Урок № 16(12)

Тема: Произведение дробей

Образовательная цель: Рассмотреть теоретические аспекты произведения дробей ;закрепить представления о рациональных выражениях; формировать представления о преобразовании рациональных выражений.

Развивающая цель: память, логическое мышление, активизация мыслительной деятельности.

Воспитательная цель: самостоятельность, дисциплинированность, точность и аккуратность ведения математической записи.

Тип урока .Урок формирования умений и навыков.

Метод. Словесный, беседа,рассказ.

Литература / основная/ Алгебра. 8 класс: учеб. для общеобразоват. организаций/ .—5-е изд.- М. : Просвещение, 2016.

Оборудование : мел, доска

Дидактический , раздаточный материал.

Ход урока

1.Организационный момент.

Проверка посещаемости;

Проверка домашнего задания

2. Мотивация учебной деятельности ,тема и цель урока.

Вы умеете умножать обыкновенные дроби ,закрепим представления о рациональных выражениях. Введем правило умножения и возведения рациональных дробей в степень.

3.Формирование умений и навыков вспомним правило умножения обыкновенных дробей.          

Для того чтобы умножить дробь на дробь, надо числитель умножить на числитель, а знаменатель на знаменатель и первое произведение записать в числителе новой дроби, второе – в знаменателе.

Например

Аналогичным образом происходит умножение рациональных дробей. Давайте докажем, что это правило на самом деле действует при умножении рациональных дробей.

Иначе говоря, докажем, что произведение двух рациональных дробей тождественно равно дроби, у которой числитель равен произведению числителей, а знаменатель – произведению знаменателей перемножаемых дробей при любых допустимых значениях переменных, кроме b равное нулю и d равное нулю.

Получили, что равенство верно при любых допустимых значениях переменных, т.е. является тождеством.

Правило умножения рациональных дробей:

Чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе – знаменателем дроби.

В буквенном виде это правило записывают так:  

Это правило выполняется и когда произведение трёх и более рациональных дробей.

Прежде чем выполнять умножение рациональных дробей, полезно их числители и знаменатели разложить на множители. Это облегчит сокращение той рациональной дроби, которая получится в результате умножения.

Пример 1: умножить дроби.

Решение:

Пример 2: умножить дроби.

Решение:

Пример 3: Представить произведение дробей в виде рациональной дроби.

Решение:

Пример 4: выполнить умножение.

Решение:

Теперь

Решение в классе №№

Рефлексия учебной деятельности на уроке. Подведение итогов урока.

6.Оценивание.

7. Домашнее задание. Учитель пишет на доске.

Алгебра 8 класс Дата: 07.10.2020

Урок № 16(12)

Тема: Правила умножения рациональных дробей
и возведения их в степень

Цель: формировать умение умножать рациональные дроби и возводить их в степень. Развивающая цель: память, логическое мышление, активизация мыслительной деятельности.

Воспитательная цель: самостоятельность, дисциплинированность, точность и аккуратность ведения математической записи.

Тип урока. Урок формирования умений и навыков.

Дидактический раздаточный материал.

Ход урока

I. Организационный момент.

Метод. Словесный, беседа ,рассказ.

Литература / основная/ Алгебра. 8 класс: учеб. для общеобразоват. организаций/ .—5-е изд.- М. : Просвещение, 2016.

Оборудование : мел , доска

II. Устная работа.

– Вычислите:

а) ; б) ; в) ; г) ; д) ;

е) ; ж) ; з) ; и) ; к) .

III. Объяснение нового материала.

Объяснение проводить, используя аналогию с обыкновенными дробями.

В результате учащиеся должны проговаривать правила умножения рациональных дробей и возведения их в степень. Эти правила выносятся на доску.

После этого необходимо привести несколько примеров из учебника, показывающих применение данных правил.

IV. Формирование умений и навыков.

1. № 108, № 109, № 111 (а, г).

№ 109.

б) .

2. № 115, № 116.

3. № 112, № 114.

Д о п о л н и т е л ь н о можно выполнить № 118.

О т в е т: 14.

Некоторым сильным в учебе учащимся можно предложить работу по карточкам.

К а р т о ч к а № 1

1. Выполните умножение:

а) ; б) ; в) .

2. Найдите значение выражения:

при т = 2, п = –3.

К а р т о ч к а № 2

1. Выполните умножение:

а) ; б) ; в) .

2. Найдите значение выражения:

при с = 2, 

х = 6, у = –1.

V. Итоги урока.

– Домашнее задание: правило возведения рациональной дроби в степень.

№ 110, № 111 (б, в), № 113(а,г)

удобно располагать буквы и числа в числителе и знаменателе

Сформулируйте правило умножения рациональных дробей

Алгебра 8 класс Дата:13.10.2020

Урок № 19(15)

Тема: Деление дробей. Решение упражнений

Образовательная цель: закрепить какие выражения называют целыми и дробными. Закрепить преобразования с рациональными выражениями и навыки деления дробей.

Развивающая цель: память, логическое мышление, активизация мыслительной деятельности.

Воспитательная цель: самостоятельность, дисциплинированность, точность и аккуратность ведения математической записи.

Тип урока. Комбинированный.

Метод. Словесный, беседа ,рассказ.

Литература / основная/ Алгебра. 8 класс: учеб. для общеобразоват. организаций/ .—5-е изд.- М. : Просвещение, 2016.

Оборудование : мел , доска

Дидактический , раздаточный материал.

Ход урока

1. Организационный момент. Мотивация (самоопределение) к учебной

Проверка посещаемости

1. Актуализация, пробное учебное действие. - какие выражения называют целыми и дробными. Познакомимся с какие значения называют допустимыми.

научимся находить допустимые значения выражения.

1. Сформулируйте тему и цель урока.

2. Формирование умений и навыков.

Вы уже знакомы с целыми и дробными выражениями. Вспомним их определения.

Целые выражения – это выражения, составленные из чисел и переменных, содержащие действия сложения, вычитания и умножения, а также деления на число, отличное от нуля.

Урок №1

Тема: Отношения чисел и величин

Образовательная цель: ввести понятие отношения чисел, величин, членов отношения; сформулировать основное свойство отношений.

Развивающая цель: память, логическое мышление,активизация мыслительной деятельности.

Воспитательная цель: самостоятельность, дисциплинированость, точность и аккуратность ведения математической записи.

Тип урока. Комбинированный.

Метод. Словесный, беседа ,рассказ.

Литература / основная/ Математика. 6 класс: учеб. для общеобразоват. организаций/ .—6-е изд.- М. : Просвещение, 2016. -- 256 с.ил.- ( МГУ -школе).

Дидактический , раздаточный материал.

Ход урока

1. Организационный момент. Мотивация (самоопределение) к учебной деятельности. Знакомство с классом.

2. Актуализация, пробное учебное действие. Содержание учебного материала №№1-3.

Подробная фронтальная проверка.

1. Мотивация учебной деятельности .Выявление места и причины затруднения. Как будем преодолевать возникшее затруднение? Что не смогли сделать? Почему? Сформулируйте тему и цель урока.

2. Формирование умений и навыков.

№№1; 13-15 . Самостоятельная работа .

1в - №№4(а); 5(в); 6(б); 7(в, г); 9(в, е)

2в - №№4(в); 5(а); 6(г); 7(а, е); 9(г, д) У кого остались вопросы?

Включения в систему знаний и повторения №1110(1ст) «Задачи на смекалку» №№136-139

5. Рефлексия учебной деятельности на уроке. Подведение итогов урока. Анализ работы в классе.

Какая была цель?

Справились?

Что ещё не выяснили?

6.Оценивание.

7. Домашнее задание. Учитель пишет на доске.

Д/з:п 1.1; №№1, 3, 4; 5(б, г); 6(в); 7(б, д);9(б, ж);1110(2ст)

Математика 6 класс

Урок № 2

Тема: Отношения чисел и величин

Образовательная цель: ввести понятие отношения чисел, однородных величин

Развивающая цель: память, логическое мышление,активизация мыслительной деятельности.

Воспитательная цель: самостоятельность, дисциплинированость, точность и аккуратность ведения математической записи.

Тип урока. Комбинированный.

Метод. Словесный, беседа ,рассказ.

Литература / основная/ Математика. 6 класс: учеб. для общеобразоват. организаций/ .—6-е изд.- М. : Просвещение, 2016. -- 256 с.ил.- ( МГУ -школе).

Дидактический , раздаточный материал.

Ход урока

1. Организационный момент. Мотивация (самоопределение) к учебной деятельности. Проверка д/з.

№№1, 3, 4; 5(б, г); 6(в); 7(б, д);9(б, ж);1110(2ст). Исправляют ошибки.

Актуализация, пробное учебное действие. № 2 . Содержание учебного материала №№1-3.

Подробная фронтальная проверка.

1. Мотивация учебной деятельности .Выявление места и причины затруднения. Как будем преодолевать возникшее затруднение? Что не смогли сделать? Почему? Сформулируйте тему и цель урока.

2. Формирование умений и навыков.

№№ 4-8(а, в); 9(а, б); 10; 11-12(а) .

Фронтальная проверка после каждого номера.

У кого остались вопросы?

Включения в систему знаний и повторения №№13(а)

№№ 14-19(а, в, д) №20

5. Рефлексия учебной деятельности на уроке. Подведение итогов урока. Анализ работы в классе.

Какая была цель?

Справились?

Что ещё не выяснили?

6.Оценивание.

7. Домашнее задание. Учитель пишет на доске.

Д/з: п1.1; №№1-3; 10(а, г); 11(а, г); 12(б, д); 13-19(б)

Математика 6 класс

Урок № 3

Тема: Масштаб.

Образовательная цель: ввести понятие масштаба, учить определять масштаб и решать обратные задачи.

Развивающая цель: память, логическое мышление, активизация мыслительной деятельности.

Воспитательная цель: самостоятельность, дисциплинированность, точность и аккуратность ведения математической записи.

Тип урока. Комбинированный.

Метод. Словесный, беседа, рассказ.

Литература / основная/ Математика. 6 класс: учеб. для общеобразоват. организаций/ .— 6-е изд.- М. : Просвещение, 2016. -- 256 с.ил.- ( МГУ -школе).

Дидактический , раздаточный материал.

Ход урока

1. Организационный момент. Мотивация (самоопределение) к учебной деятельности. Проверка д/з.

1-3; 10(а, г); 11(а, г); 12(б, д); 13-19(б)

Исправляют ошибки.

1. Актуализация, пробное учебное действие.

Что же такое масштаб? Каким он бывает? Как масштаб связан с отношением чисел?

1. Мотивация учебной деятельности .Выявление места и причины затруднения. Почему не смогли ответить на вопросы? Сформулируйте цель урока. Как будем преодолевать возникшее затруднение?

Читают, маркируют, обсуждают текст. Фронтальная проверка.

1. Формирование умений и навыков. №№16; 18-20

№№21, 22(1, 3ст); 23(а, в); 24(а, в, г, е); 25; 27. Фронтальная проверка после каждого номера.

У кого остались вопросы? Возврат к поставленным вопросам. Помогаю отдельным группам по сигналу.

Включения в систему знаний и повторения №№10-11(б, д, в, е); 12(в, е) №№15 -19(г) – у доски.

5. Рефлексия учебной деятельности на уроке. Подведение итогов урока. Анализ работы в классе.

Какая была цель?

Справились?

Что ещё не выяснили?

6.Оценивание.

7. Домашнее задание. Учитель пишет на доске.

Д/з:п 1.2; №№21; 22(2, 4ст); 23(б); 24(б, д); 26

Математика 6 класс

Урок № 4,

Тема: Масштаб

Образовательная цель: закреплять изученный материал, учить применять знания на практике.

Развивающая цель: память, логическое мышление, активизация мыслительной деятельности.

Воспитательная цель: самостоятельность, дисциплинированность, точность и аккуратность ведения математической записи.

Тип урока. Комбинированный.

Метод. Словесный, беседа, рассказ.

Литература / основная/ Математика. 6 класс: учеб. для общеобразоват. организаций/ .— 6-е изд.- М. : Просвещение, 2016. -- 256 с.ил.- ( МГУ -школе).

Дидактический , раздаточный материал.

Ход урока

1. Организационный момент. Мотивация (самоопределение) к учебной деятельности. Проверка д/з.

№№1, 3, 4; 5(б, г); 6(в); 7(б, д);9(б, ж);1110(2ст). Исправляют ошибки.

Актуализация, пробное учебное действие. п 1.1; 1.2; ? по д/з

2) №№28-29(а)

1. Актуализация базовых знаний.

Что же такое масштаб? Каким он бывает? Как масштаб связан с отношением чисел?

3.Мотивация учебной деятельности .Выявление места и причины затруднения. Почему не смогли ответить на вопросы? Сформулируйте цель урока. Как будем преодолевать возникшее затруднение?

Читают, маркируют, обсуждают текст. Фронтальная проверка.

4.Формирование умений и навыков.

1)На какое правило допущена ошибка? Как будете работать? 2) №№ 32-34 №№ 28-29 (б)

Фронтальная проверка после каждого номера. Локализация индивидуальных затруднений.

У кого остались вопросы? Возврат к поставленным вопросам. Помогаю отдельным группам по сигналу.

Включения в систему знаний и повторения 9(в); 11(б); 12 б.

5. Рефлексия учебной деятельности на уроке. Подведение итогов урока. Анализ работы в классе.Какая была цель? Справились? Обобщение затруднений во внешней речи.Что ещё не выяснили?

6.Оценивание.

7. Домашнее задание. Учитель пишет на доске.

Д/з: п1.1; 1.2; №№31(а); 10(в, е); 11(в, е); 12(г, ж); 19(е-з)

Математика 6 класс

Урок № 5

Тема: Деление числа в данном отношении.

Образовательная цель: Учить решать задачи.

Развивающая цель: память, логическое мышление, активизация мыслительной деятельности.

Воспитательная цель: самостоятельность, дисциплинированность, точность и аккуратность ведения математической записи.

Тип урока. Комбинированный.

Метод. Словесный, беседа, рассказ.

Литература / основная/ Математика. 6 класс: учеб. для общеобразоват. организаций/ .— 6-е изд.- М. : Просвещение, 2016. -- 256 с.ил.- ( МГУ -школе).

Дидактический , раздаточный материал.

Ход урока

1. Организационный момент. Мотивация (самоопределение) к учебной деятельности. Проверка д/з.

п1.1; 1.2; №№31(а); 10(в, е); 11(в, е); 12(г, ж); 19 е-з . Исправляют ошибки.

1. Актуализация базовых знаний.

Выявление места и причины затруднения

3.Мотивация учебной деятельности . Сформулируйте цель урока.

Самостоятельная работа с самопроверкой по эталону. 4 чел. работают у доски.

Подробная проверка.

№№ 36(а); 37(1 ст) 2в 4 чел. работают у доски.

Подробная проверка

Фронтальная проверка после каждого номера. Локализация индивидуальных затруднений.

У кого остались вопросы? Возврат к поставленным вопросам. Помогаю отдельным группам по сигналу.

Включения в систему знаний и повторения работа с карточками заданиями

5. Рефлексия учебной деятельности на уроке. Подведение итогов урока. Анализ работы в классе. Какая была цель? Справились? Обобщение затруднений во внешней речи.Что ещё не выяснили?

6.Оценивание.

7. Домашнее задание. Учитель пишет на доске. Д/з: п 1.3; №38;

Математика 6 класс

Урок № 6

Тема: Деление числа в данном отношении.

Образовательная цель: Учить решать задачи.

Развивающая цель: память, логическое мышление, активизация мыслительной деятельности.

Воспитательная цель: самостоятельность, дисциплинированность, точность и аккуратность ведения математической записи.

Тип урока. Комбинированный.

Метод. Словесный, беседа, рассказ.

Литература / основная/ Математика. 6 класс: учеб. для общеобразоват. организаций/ .— 6-е изд.- М. : Просвещение, 2016. -- 256 с.ил.- ( МГУ -школе).

Дидактический , раздаточный материал.

Ход урока

1. Организационный момент. Мотивация (самоопределение) к учебной деятельности. Проверка д/з. №38;

Исправляют ошибки.

1. Актуализация базовых знаний.

Выявление места и причины затруднения 39, 41, 42 – у доски

3.Мотивация учебной деятельности . Сформулируйте цель урока.

Самостоятельная работа с самопроверкой по эталону. 4 чел. работают у доски.

Подробная проверка.

№№ 2в 4 чел. работают у доски.

Подробная проверка

Фронтальная проверка после каждого номера. Локализация индивидуальных затруднений.

У кого остались вопросы? Возврат к поставленным вопросам. Помогаю отдельным группам по сигналу.

Включения в систему знаний и повторения 1)На какое правило допущена ошибка? Как будете работать?

2) «Задачи на смекалку» №№140-143

5. Рефлексия учебной деятельности на уроке. Подведение итогов урока. Анализ работы в классе. Какая была цель? Справились? Обобщение затруднений во внешней речи.Что ещё не выяснили?

6.Оценивание.

7. Домашнее задание. Учитель пишет на доске. Д/з: п 1.3; №№40; 1111; 1112

Математика 6 класс

Урок № 7

Тема: Деление числа в данном отношении.

Образовательная цель: Учить решать задачи.

Развивающая цель: память, логическое мышление, активизация мыслительной деятельности.

Воспитательная цель: самостоятельность, дисциплинированность, точность и аккуратность ведения математической записи.

Тип урока. Комбинированный.

Метод. Словесный, беседа, рассказ.

Литература / основная/ Математика. 6 класс: учеб. для общеобразоват. организаций/ .— 6-е изд.- М. : Просвещение, 2016. -- 256 с.ил.- ( МГУ -школе).

Дидактический , раздаточный материал.

Ход урока

1. Организационный момент. Мотивация (самоопределение) к учебной деятельности. Проверка д/з. №38;

Исправляют ошибки.

1. Актуализация базовых знаний.

Выявление места и причины затруднения 1)№№40; 1111; 1112

2)№№43; 44(в, г)

3.Мотивация учебной деятельности . Какие задачи учимся решать?

Какую цель поставим сегодня? (Корректировать выявленные затруднения.)

Подробная проверка.

№№ )№№1113-1114(а) №44(а, б)

Фронтальная проверка после каждого номера. Локализация индивидуальных затруднений.

У кого остались вопросы? Возврат к поставленным вопросам. Помогаю отдельным группам по сигналу.

Включения в систему знаний и повторения 1)На какое правило допущена ошибка? Как будете работать?

2) «Задачи на смекалку» №№144-147 по выбору

5. Рефлексия учебной деятельности на уроке. Подведение итогов урока. Анализ работы в классе. Какая была цель? Справились? Обобщение затруднений во внешней речи. Что ещё не выяснили?

На какое правило допущена ошибка? Как будете работать?

№№1113-1114(а)

6.Оценивание.

7. Домашнее задание. Учитель пишет на доске. Д/з: п 1.3; : №№44(д); 1113-1114(б, в)

Математика 6 класс

Урок № 8

Тема: Пропорции

Образовательная цель: Учить решать пропорции

Развивающая цель: память, логическое мышление, активизация мыслительной деятельности.

Воспитательная цель: самостоятельность, дисциплинированность, точность и аккуратность ведения математической записи.

Тип урока. Комбинированный.

Метод. Словесный, беседа, рассказ.

Литература / основная/ Математика. 6 класс: учеб. для общеобразоват. организаций/ .— 6-е изд.- М. : Просвещение, 2016. -- 256 с.ил.- ( МГУ -школе).

Дидактический , раздаточный материал.

Ход урока

1. Организационный момент. Мотивация (самоопределение) к учебной деятельности №№ 45-47; 48-51(1ст); 52. Проверка Исправляют ошибки.

2. Актуализация базовых знаний.

Выявление места и причины затруднения 1)№№40; 1111; 1112

2)№№43; 44(в, г)

3.Мотивация учебной деятельности . Какие задачи учимся решать?

Какую цель поставим сегодня? (Корректировать выявленные затруднения.) а) ;

б) ; в) №№53-58(а, в)

Фронтальная проверка Локализация индивидуальных затруднений.

У кого остались вопросы? Возврат к поставленным вопросам. Помогаю отдельным группам по сигналу.

Включения в систему знаний и повторения

1) На какое правило допущена ошибка? Как будете работать?

2) «Задачи на смекалку» №№148-154

5. Рефлексия учебной деятельности на уроке. Подведение итогов урока. Анализ работы в классе. Какая была цель? Справились? Обобщение затруднений во внешней речи. Что ещё не выяснили?

6.Оценивание. Справились? Что ещё не выяснили?

7. Домашнее задание. Учитель пишет на доске. Д/з: п 1.4; №№45; 53-58(б, г) – не менее 7 пропорций