Урок по алгебре "Урок одного уравнения"

ДОКЛАД

на тему:

« Тригонометрические функции в музыке»

Ученика 10А кл. МОУСОШ № 4

Дубровского А.

2011г.

СОДЕРЖАНИЕ

I. Базовые понятия музыкальной акустики

1. Свободные колебания вибраторов в музыкальных инструментах

2.Вынужденные колебания источников звука в музыкальных инструментах

2

I.Базовые понятия музыкальной акустики

Если мы сравним записи звучания двух разных оркестров, например симфонического и джазового, то, к нашему удивлению, нам будет чрезвычайно трудно найти какое-либо характерное различие записанных кривых. Они очень сложны. Мы с гораздо большим успехом сможем заняться изучением сначала простейших колебаннй. График простейшего колебания представляет собой синусоиду, которая в свою очередь является «портретом» чистого музыкального тона, который звучит довольно глухо и малоинтересен с музыкальной точки зрения. но имеет ярко выраженную определенность высоты {схема 1). Сравним синусоиду с графиком «белого шума» (схема 2), примером которого является шум аплодисментов или шум морского прибоя и который не имеет какой-либо определенной высоты. Кривая такого графика больше похожа на случайный, хаотичный набор импульсов.

3

Схема 1. Простое гармоническое колебание. AB – период, DE и GF – амплитуда

Схема 2. Белый шум

Схемы 1 и 2 представляют два крайних по свойствам звука. Можно сказать, что все другие сложные звуки находятся между этими двумя крайностями: полной регулярности и полной нерегулярности. Начнем с изучения простейших колебаний.

Физическая сущность колебательных процессов, происходящих в вибраторах музыкальных инструментов, различна. Причины колебаний, например, струны, возбужденной ударом, отличаются от причин колебаний язычка в проеме голосовой планки, на который действует поток воздуха, и совсем другая причина колебаний столба воздуха в трубе духового музыкального инструмента. Но даже первое знакомство с законами колебаний вибраторов музыкальных инструментов обнаруживает много одинакового в самих колебательных движениях этих вибраторов.

4

1. Свободные колебания вибраторов в музыкальных инструментах

При изучении колебаний обычно не интересуются положением точки в данный момент времени. Например, струна издает звук ля. В какой-то момент времени мы слышим этот звук, но он не определяется положением струны в данный момент времени, а зависит от всего процесса колебаний струны в целом. Установление общих закономерностей всего процесса в целом характерно для рассмотрения различных типов колебаний источников музыкальных звуков.

Посмотрим, каковы колебания точки, находящейся на торце вилки камертона. По движению одной точки еще нельзя судить о движении многих других точек вибратора, и правомерен вопрос: можно ли отождествлять колебания одной точки с колебаниями источника, на котором взята эта точка? Теория колебаний показывает, что такое отождествление хотя и незаконно во всех случаях, но часто весь процесс колебаний может быть представлен так же, как и движение одной единственной точки.

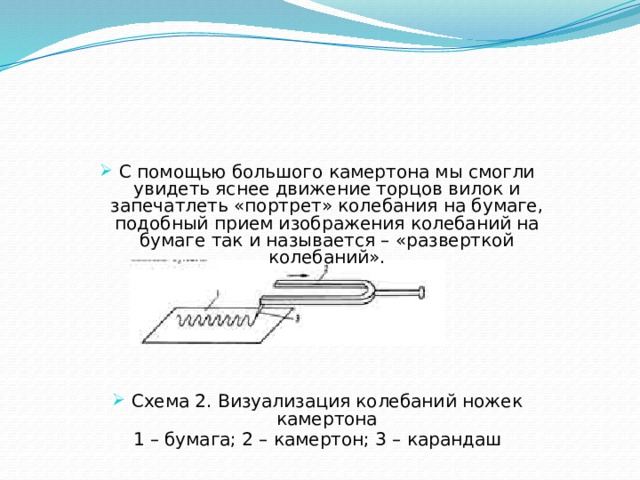
Как сделать видимыми колебания точки на торце вилки камертона? Можно, конечно, мысленно представить себе, что вилки камертона попеременно то сближаются, то удаляются. Обычный камертон стандарта высоты ля1 не позволит увидеть движение, но если взять большой камертон и прикрепить к одной вилке кусочек грифеля от карандаша, то движение можно сделать видимым. Нужно только быстро и легко провести грифелем на колеблющемся камертоне по полоске бумаги.

Схема 3. Визуализация колебаний ножек камертона

1 – бумага; 2 – камертон; 3 – карандаш

Таким образом, с помощью большого камертона мы смогли увидеть яснее движение торцов вилок и запечатлеть «портрет» колебания на бумаге. Колебания как бы развернулись во времени; подобный прием изображения колебаний на бумаге так и называется – «разверткой колебаний». Кстати сказать, развертка колебаний может быть осуществлена и другими путями, например, с помощью электронного луча на экране электронно-лучевой трубки.

5

Камертон можно заставить звучать не только ударом, но и проводя по нему смычком. В этом случае портрет колебаний изобразится плавной кривой – синусоидой. Синусоида – графическое представление какой-либо переменной величины, изменяющейся по закону синуса. В нашем случае так изменяется во времени положение точки на торце вилки камертона.

Многие физические явления в природе происходят в соответствии с законом синуса. Строгая математика считает синусоидальным только такое колебание, которое никогда не начиналось и никогда не кончается. Естественно, что реальные колебательные процессы никогда такому условию не отвечают. Все имеет свое начало и конец. Поэтому принято считать колебания синусоидальными, если они являются таковыми хотя бы на конечном, достаточно длительном отрезке времени.

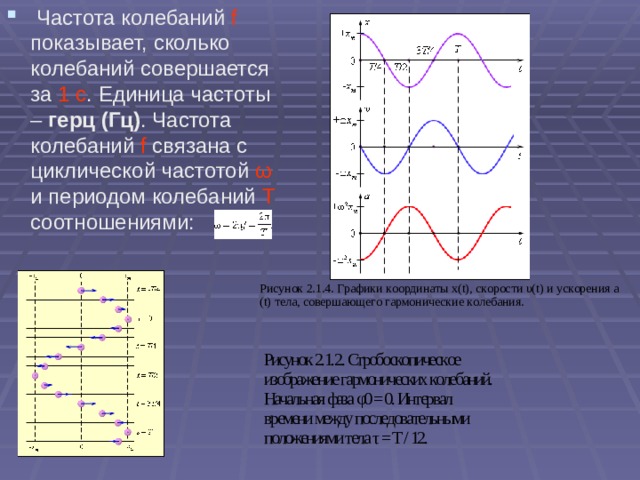
Для колебания, представленного на схеме 1, рассмотренные только что параметры – период, частота и амплитуда – постоянные во времени величины. Они постоянны и в первую, и во вторую, и в третью, и в последующие секунды. Но каким же образом постоянные величины могут представлять само движение точки? Мы еще не сказали об одной переменной величине, которая несет непосредственную информацию о движении и зависит от констант (постоянных величин) колебательного процесса. Эта переменная величина – отклонение колеблющейся точки от положения равновесия в данный момент времени. Когда отклонение максимальное, его называют амплитудой, как и было уже установлено выше. Если мы будем знать закон изменения отклонения y во времени, то тем самым будем знать практически все о данном процессе колебания.

Графически закон изменения отклонения во времени уже представлен кривой на схеме, т. е. синусоидой. Поэтому остается только представить эту кривую с помощью соответствующей формулы:

у=А * Sin 2πf * t, (1)

где: А — амплитуда колебания,

f – частота колебания (f = 1/T, где Т — период),

2π – постоянный коэффициент (π = 3,14),

t – текущее время,

у – отклонение колеблющейся точки от положения равновесия в данный момент времени t.

Обозначим произведение постоянного коэффициента 2π на частоту f буквой ω, которую назовем, в отличие от циклической частоты f, круговой частотой: 2πf = ω. Это обозначение будет использовано ниже.

6

Любое колебательное движение, совершающееся по закону (1), называется гармоническим колебанием.

Изменения параметров гармонического колебания вызывают соответствующие изменения тона. Так, увеличение амплитуды вызывает увеличение громкости, а уменьшение или увеличение частоты – понижение или повышение тона. А существует ли связь между амплитудой и частотой? Зависит ли частота от того, насколько сильно возбудили камертон или струну? Ответ – и да, и нет – может показаться на первый взгляд парадоксальным. Из логики ведь известно. что два противоположных суждения об одном и том же предмете не могут быть одновременно истинными, какое-то суждение должно быть ложным. Однако логика такого ответа будет спасена, если учесть, с какой точностью определять изменение частоты при изменении амплитуды.

В первом прнближении можно считать, что параметры не зависят для большинства вибраторов один от другого, если амплитуды колеблющихся струн или язычков достаточно малы. Такое свойство колебаний называется изохронностью, Практически человек не замечает изменения частоты, если первый раз сыграть тон очень тихо (пианиссимо), а второй раз – очень громко (фортиссимо). Да иначе и нельзя было бы играть на инструментах, в которых при изменении громкости изменялась бы частота.

И все же небольшие отклонения от изохронности наблюдаются даже у признанного эталона частоты — камертона: частота очень слабых его колебаний чуть-чуть ниже частоты сильных колебаний. Но ухо таких отклонений частоты попросту не замечает. В данной книге рассматриваются только изохронные колебания или, как их иначе называют, линейные колебания. Если же изохронность нарушается, то колебания называют нелинейными. Большинство вибраторов музыкальных инструментов при очень сильных колебаниях, то есть, больших амплитудах дают нелинейные колебания или, как говорят, становятся нелинейными системами. Но при достаточно малых амплитудах колебания в музыкальных инструментах можно считать линейными.

Мы установили, что гармонические колебания камертона имеют определенную частоту (или обратную ей величину – период) и амплитуду. Допустим, два одинаковых камертона имеют одинаковые амплитуды и частоты. Могут ли чем-то отличаться колебания этих камертонов? Оказывается. могут. Один камертон можно заставить звучать несколько позже, чем другой. Соответствующие графики колебаний будут смещены друг относительно друга (см. схему 4). Такому смещению дали специальное обозначение – с д в и г или, что более употребителыю, разность фаз. Разность фаз определяется расстоянием, отсчитанным по оси времени (горизонтальной оси), однако это смещение по времени удобнее выразить в долях мериода, короче говоря, сопоставить смещение с величиной периода.

7

Схема 4. Сдвиг фаз колебаний

Предположим, что в какой-то момент вилки одного камертона отклонились от положения равновесия на максимальную величину, а в тот же самый момент вилки второго камертона проходят положение равновесия. Синусоиды в этом случае сдвинуты на четверть периода (см. схему 4), и колебания различаются по фазе на 90° (полный период принят за 360°).

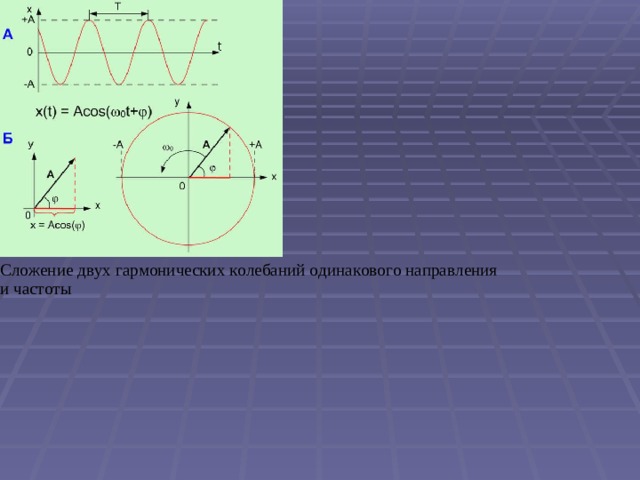
Для настройки важную роль, как увидим далее, играет разность фаз 0° и разность фаз 180°. Соответствующие пары синусоид показаны на схемах 5 и 6. При нулевой разности фаз графики колебаний

Схема 5. Сложение гармонических колебаний с равными частотами, разность фаз φ = 0о

8

Схема 6. Сложение гармонических колебаний с равными частотами, разность фаз φ = 180о

камертонов точно совпадают, такие колебания называются с и н ф а з н ы м и. При разности фаз 180° колебания являются как бы зеркальным отражением друг друга. В этом случае вилки одного камертона максимально раздвинуты, а вилки второго камертона максимально сближены в тот же самый момент, в следующий момент положение вилок меняется на противоположное и т. д. Если частоты камертонов в точности совпадают, а разность фаз сохраняется постоянной (и не обязательно равной нулю), то такие колебания называют с и н х р о н н ы м и. Синхронизация колебаний имеет место, например, при настройке унисона. Отметим также, что колебания с разностью фаз 180° называются антифазными, сами колебания происходят в противофазе.

Сдвиг фаз рассматривался до сих пор как характеристика временного смещения колебаний. Но можно установить понятие фазы и для одного гармо-нического колебания. Тогда фазу, выраженную в долях периода, нужно отсчитывать от какого-либо произвольно выбранного момента времени. Обычно рассматривают так называемую начальную фазу, которая характеризует состояние гармонического колебания в начальный момент времени, и обозначают ее буквой φ0.

Начальная фаза колебаний вибратора в музыкальном инструменте зависит от способа его возбуждения. Так, для струны фортепиано, возбужденной ударом молотка, начальная фаза будет равна нулю, так как струна практически мгновенно начинает двигаться из своего положения равновесия. Напротив, струна щипкового инструмента, оттянутая в сторону и отпущенная, начинает свои колебания от максимального отклонения от положения равновесия, и фаза такого колебания струны будет равна не нулю, а 90°.

9

Теперь можно заполнить три графы «анкеты» любого гармонического колебания: частота, амплитуда и фаза. Эти параметры остаются постоянными в течение всего процесса и характеризуют колебание в целом, в отличие от переменных «отклонения у» и «времени t», характеризующих положение колеблющейся точки во времени. С учетом «анкетных данных» гармоническое колебание может быть записано аналитически в следующем виде:

у = А*Sin (ωt - φ0), (2)

где: у — отклонение точки от положения равновесия в данный мо-

мент времени t,

А – амплитуда,

ω — круговая частота,

t – время,

φ0 – фаза колебания (начальная фаза).

Отклонение у колеблющейся точки от положения равновесия по вышеприведенной формуле (2) можно связать с параметрами вибратора. Какие же в данном случае нужны параметры вибратора? Существует два обобщенных параметра любой колеблющейся системы, влияющие на частоту колебаний: это упругость и масса вибратора. Они обозначаются, соответственно, буквами k и m.

Коэффициент k называют еще жесткостью. Физический смысл этого коэффициента проще всего пояснить на примере пружины с грузом, который может колебаться на пружине, если второй конец пружины неподвижно закреплен в опоре: коэффициент k численно равен усилию в пружине при ее растяжении (или сжатии) на единицу длины (см). В струне коэффициент жесткости увеличивается с повышением натяжения струны, в язычке этот коэффициент можно уменьшить, подпилив язычок у основания. Выяснив теперь физический смысл упругости (жёсткости) вибратора, мы без труда поймем и связь параметров вибратора с частотой, устанавливаемую основной формулой для колебаний материальных тел:

ω = √k/m, (3)

где k и m — рассмотренные выше упругость и масса.

Значение частоты из формулы (3) можно подставить в уравнение (2). Тогда окажется, что весь процесс гармонического колебаиия зависит от четырех постоянных параметров: упругости и массы тела, с одной стороны, и амплитуды и начальной фазы – с другой. Два первых постоянных параметра выражают динамические свойства вибратора, а два последних – так называемые начальные условия колебаний (где рассматриваемая точка находилась и какую скорость имела в начальный момент времени).

10

Современные средства физического эксперимента позволяют записать затухающие колебания вибратора музыкального инструмента. Самой простой записью оказывается опять-таки кривая затухающих колебаний камертона, изображенная на схеме 10.

Схема 10. Затухающие колебания

Эта кривая — не синусоида, не гармоническое колебание, и можно лишь с большой натяжкой считать ее синусоидальным колебанием, амплитуда которого убывает со временем. На схеме 10 по вершинам синусоид проведена кривая, называемая экспонентой, она как бы показывает, что уменьшение амплитуды происходит по экспоненциальному закону: е –αt , а само колебание происходит по закону синуса: А Sin ωt. Тогда затухающее колебание можно представить формулой:

y = A e-αt Sin ωt (6)

в которой требует расшифровки только множитель e-αt . Здесь е —основание натуральных логарифмов, равное 2,718, а коэффициент α называется коэффициентом затухания колебания. Он характеризует уменьшение амплитуды колебаний за единицу времени и обратно пропорционален времени, в течение которого амплитуда убывает в е (« 3) раз. Если α мало, то убывание амплитуды происходит медленно. Затухающее колебание можно характеризовать еще одним параметром: логарифмическим декрементом колебания, который получается, если взять натуральный логарифм отношения двух соседних амплитуд:

δ = ln (An /An+1) = α T (7)

Декремент колебания характеризует уменьшение амплитуды за один период и обратно пропорционален числу колебаний, по истечении которых амплитуда спадает в е раз. Приведем пример. Хороший камертон имеет δ = 1/10 000. Это значит, что амплитуда колебаний уменьшится в е раз через 10000 колебаний.

11

Часто для характеристики вибраторов употребляется еще такая величина, как добротность:

Q = π/ δ (8)

которая тем больше, чем дольше длительность свободных затухающих колебаний вибратора. Есть и другой смысл понятия добротности: она показывает, во сколько раз увеличивается амплитуда вибратора в момент резонанса по сравнению с амплитудой прогиба вибратора при статическом приложении силы той же самой величины.

12

2. Вынужденные колебания источников звука в музыкальных инструментах

Во многих музыкальных инструментах для приведения в колебательное движение вибратора используется внешняя сила. При этом вибратор совершает вынужденные колебания. Пример вынужденных колебаний — движение язычка под действием воздушного потока, колебания столба воздуха в трубе, совершающиеся в результате периодических толчков воздуха со стороны мундштука, наконец, колебания деки в струнных инструментах под воздействием вибраций струн.

Имеются две принципиальные возможности заставить вибратор колебаться: подводить к нему внешнюю периодическую силу, и тогда частота колебаний вибратора будет определяться частотой колебаний вынуждающей силы, или же внешняя сила будет сообщать вибратору только энергию, не являясь сама периодической. Вибратор в этом последнем случае возбуждается на собственной частоте, той частоте, с которой он колебался бы свободно.

Рассмотрим прежде всего вынужденные колебания, возбуждаемые гармонической внешней силой. Нас прежде всего интересует вопрос, что происходит с простой колебательной системой, когда на нее воздействует периодическая сила? Какими особенностями будет характеризоваться движение сразу же после приложения силы и далее в течение последующего времени? Интерес представляет и вопрос зависимости колебаний от частоты вынуждающей силы. В начальный момент приложения внешней силы отклонение равно нулю, и затем колебательная система будет все больше и больше раскачиваться (см. схему 11).

Схема 11. Вынужденные колебания 1 — периодическая внешняя сила; собственные затухающие колебания вибратора; 3 — вынужденные колебания вибратора

13

Как правило, движение происходит по сложному закону и может рассматриваться как результат сложения двух колебательных движений: собственных затухающих колебаний и периодических колебаний внешней силы. Через некоторое время собственные колебания затухнут и установятся колебания с постоянной амплитудой, процесс нарастания амплитуды прекратится. Таким образом, прежде чем колебания установятся, происходит процесс раскачки системы. Данная часть процесса называется процессом установления колебаний или в общем случае — переходным процессом, за которым следует процесс стационарных (или установившихся) колебаний. Время нарастания колебаний от нуля до некоторого стационарного значения называется временем у с т а н о в л е н и я колебаний и обозначается tу. Характер переходного процесса оказывает влияние на тембр звука, точно так же как спектр влияет на окраску звука.

Одна из характеристик переходного процесса — время установления колебаний. Если раскачка колебаний происходит относительно быстро, как, например, при ударе молотка фортепиано по струне, то такой процесс нарастания колебаний называют ж е с т к о й а т а к о й, при относительно медленном нарастании колебаний, например, у гармонного язычка – мягкой атакой.

Установившиеся колебания не зависят от того, каким путем вибратор был приведен в движение. Но основные параметры вынужденного колебания — частота, амплитуда и фаза зависят от частоты и амплитуды вынуждающей силы и от массы, упрутости и затухания вибратора музыкального инструмента. Важную роль играет соотношение собственной частоты вибратора и частоты вынуждающей силы.

14

Урок алгебры в 10-м классе "Решение тригонометрических уравнений"

Цели урока:

Главная цель: Развитие интеллекта и мышление ребенка

Обучающие:

• Применение различных способов решения уравнения sinx +cosx=1;

• Знакомство с новым способом решения уравнения, через введение вспомогательного угла;

• Формирование умений применять полученные знания по математике на уроках физики, музыки, геометрии, т.е. формирование целостного мировосприятия:

• Отработка у учащихся приемов учебно-познавательной деятельности;

• Активизирование личностного смысла учащихся к изучении темы.

Развивающие:

• Развитие творческих способностей и познавательного интереса;

• Развитие самостоятельности учащихся в выборе способа решения уравнения sinx +cosx=1;

• Развитие общекультурного уровня устной речи учащихся;

• Развитие навыков самостоятельности и работы в группах.

Воспитательные:

• Воспитание воли и настойчивости в достижении конечного результата;

• Стимулирование любознательности, творческой деятельности;

• Критичности мышления;

• Сознательное отношение к учебе и коммуникативных умений

Задачи урока:

• Организовать деятельность учащихся по обобщению и систематизации знаний решения тригонометрических уравнений через решения уравнения вида sinx +cosx=1;

• Развивать интерес учащихся к занятию, придав ему проблемно-исследовательский характер, что отвечает личностным интересам и потребностям учащихся;

• Развивать потребность в исследовательской деятельности.

Основные этапы урока

1. Организационный момент (2 мин.)

2. Актуализация опорных знаний и умений (5 мин.)

3. Решение уравнения sinx + cosx=1; (6 способов) (15 мин.)

4. Знакомство с новым способом: введение вспомогательного угла (15 мин.)

5. Подведение итога урока и постановка домашнего задания (3 мин.)

ХОД УРОКА

Лучше всего продвигается   естественное исследование,
когда физическое завершается в математическом
Ф.Бэкон (1561-1626)
английский философ

1. Организационный момент.

Задача этапа: Создать у учащихся рабочий настрой и обеспечить деловую обстановку в классе.

Метод обучения: словесный.

Форма обучения: коллективная.

Деятельность учителя: Приветствие учащихся. Цитирует эпиграф. Сообщает тему урока: “У нас сегодня урок одного уравнения. Вам было дано задание на дом найти, как можно способов решения уравнения sinx + cosx=1. Работа велась в группах. Мы проверим, чья группа нашла больших способов решения этого уравнения уравнений и познакомимся со способом решения уравнения через введение вспомогательного угла, понятие которого используется в гармонических колебаниях, т.е. тем самым установим связь с физикой и музыкой.

Деятельность учащихся:

Приветствуют учителя. Слушают. Записывают тему урока.

2. Актуализация опорных ЗУН.

2.1.На этапе актуализации знаний происходит воспроизведение и коррекция необходимых знаний и умений.

Ребята, предложившие свой способ, проходят к доске и решают. В это время проводится программированный контроль ЗУН по решению простейших уравнений:

ПОКАЗАТЬ ИЗ ЦОРов ОБЪЯСНЕНИЕ ХОТЯ БЫ ОДНОГО УРАВНЕНИЯ - это № 44

Устная работа № 44 - проверка знаний

2.2.Презентация учащегося по теме «История тригонометрии»

2.3.Презентация учащегося, увлекающегося физикой:

Тригонометрические функции широко применяются в математике, физике, технике. Такие процессы как колебание пружины, колебание маятника, напряжение в цепи переменного тока описываются функцией, которая задается формулой у = Аsin (ωx +φ)

Например

1. Конец упругой пружины (точка Р) описывает колебательные движения зависимость координаты Р от времени t будет иметь вид х = Аsin (ωt +П/2) ω- коэффициент упругости пружины.

2. Электрический колебательный контур

Если взять электрическую цепь, состоящую из последовательно соединенных конденсатора С и катушки индуктивности L и замкнуть, то по цепи пойдет ток, напряжение которого будет меняться со временем и эта зависимость будет иметь вид U = U₀ sin (ωt +α)

Мы видим, что и эта зависимость выражается формулой вида у = Аsin (ωx +φ).

2.4.Презентация учащегося, увлекающегося музыкой (гитара).

3. Чистый звуковой тон представляет собой колебание с некоторой постоянной частотой. Чистый тон можно представить в виде любой ноты. Наложение тонов - это любой аккорд. Высота звука зависит от октавы. Чем больше октава, тем выше звук. Чем ниже октава, тем ниже звук. Высота звука определяется частотой колебания Музыка, которую мы слышим, представляет собой наложение различных чистых тонов. Преобладание той или иной частоты (скажем, низких или высоких) связано с амплитудой соответствующих колебаний. На языке математики это означает, что любую периодическую функцию можно представить с наперед заданной точностью как сумму синусов. Этот замечательный факт обнаружил еще в XVIII веке Бернулли при решении задачи о колебании струны.

Учащиеся осмысливают практическую значимость, полезность приобретенных знаний и умений, происходит выявление личностного отношения через межпредметную связь).

Поддерживать учащихся, проявлять и развивать свои способности, обеспечивать успешное протекание процессов самопознания и самореализации (осознанное восприятие материала)

3. Решение уравнения sinx +cosx=1.

Задача этапа: продолжить формирование мотивации учения учащихся, закрепляя уверенность в себе: “Я умею - я знаю - я могу”. Формирование целостного мировосприятия

Методы обучения: словесный, частично-поисковый.

Форма обучения: групповая, коллективная и индивидуальная.

Аукцион идей (каждая группа как можно больше предлагает способов решения).

Осуществляется самоконтроль и взаимоконтроль. Обращение к имеющимся знаниям детей, понятийность через интерес самих детей. Выслушивание различных точек зрения. Учащиеся учатся слышать друг друга, уступать или отстаивать свою точку зрения. Данная форма работы побуждает и развивает у ребят исследовательский инстинкт, развивает способность анализировать, обобщать, выделять главное.

Предложив способ решения – учащийся выходит к доске и решает самостоятельно.

1 способ (разложением на множители)

sinx +cosx=1 (используя формулы двойного угла)

2 способ (приведение к однородному уравнению второй степени)

3 способ (преобразование суммы тригонометрических функций в произведение)

4 способ (выражение всех функций через tg x (универсальная подстановка)

5 способ (возведение в квадрат обеих частей уравнения)

6 способ (введение вспомогательного угла)

Подведение итога урока и домашнее задание

Рефлексия

• Сегодня на уроке я узнал, что…

• Я прочитаю…

• Мне понравилось…

• Я бы хотел...

Дома: Решить задачу.

Определить углы прямоугольного треугольника, если длины его сторон являются тремя последовательными членами арифметической прогрессии.

Решить уравнения через введение вспомогательного угла.

Поделиться

1. История создания тригонометрии.

2. Основные тригонометрические тождества.

3. Тригонометрические выражения.

4. Формулы приведения.

5. Решение прямоугольных треугольников.

6. Обратные тригонометрические функции.

7. Используемая литература.

Возникновение

тригонометрии

Тригонометрия – слово греческое и в буквальном переводе означает измерение треугольников (trigwnon - треугольник, а metrew- измеряю).

В данном случае измерение треугольников следует понимать как решение треугольников, т.е. определение сторон, углов и других элементов треугольника, если даны некоторые из них. Большое количество практических задач, а также задач планиметрии, стереометрии, астрономии и других приводятся к задаче решения треугольников.

Возникновение  тригонометрии связано с землемерием, астрономией и строительным делом.

Хотя название науки возникло сравнительно недавно, многие относимые сейчас к тригонометрии понятия и факты были известны ещё две тысячи лет назад.

Впервые способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом (2 в. до н. э.) и Клавдием Птолемеем (2 в. н. э.). Позднее зависимости между отношениями сторон треугольника и его углами начали называть тригонометрическими функциями.

Гиппарх Клавдий Птолемей

Значительный вклад в развитие тригонометрии внесли арабские ученые Аль-Батани (850-929) и Абу-ль-Вафа, Мухамед-бен Мухамед (940-998), который составил таблицы синусов и тангенсов через 10’ с точностью до 1/60⁴. Теорему синусов уже знали индийский ученый Бхаскара (р. 1114, год смерти неизвестен) и азербайджанский  астроном и математик Насиреддин Туси Мухамед (1201-1274). Кроме того, Насиреддин Туси в своей работе «Трактат о полном четырехстороннике» изложил плоскую и сферическую тригонометрию как самостоятельную дисциплину.

Мухамед-бен Мухамед Бхаскара Насиреддин Туси

Длительную историю имеет понятие синус. Фактически различные отношения отрезков треугольника и окружности (а по существу, и тригонометрические функции) встречаются уже в III веке до н.э. в работах великих математиков Древней Греции – Евклида, Архимеда, Апполония Пергского. В римский период эти отношения достаточно систематично исследовались Менелаем (I век н.э.), хотя и не приобрели специального названия.  Современный синус a, например, изучался как полухорда, на которую опирается центральный угол величиной a, или как хорда удвоенной дуги.

Евклид Архимед Апполоний Пергский

                                     А           A

                                               А’

Рис. 1

В IV-V веках появился уже специальный термин в трудах по астрономии великого индийского учёного Ариабхаты, именем которого назван первый индийский спутник Земли. Отрезок АМ (рис. 1) он назвал ардхаджива (ардха – половина, джива – тетива лука, которую напоминает хорда). Позднее появилось более краткое название джива. Арабскими математиками  в IX веке это слово было заменено на арабское слово джайб (выпуклость). При переводе арабских математических текстов в  веке оно было заменено латинским синус (sinus – изгиб, кривизна)

Ариабхат

Слово косинус намного моложе. Косинус – это сокращение латинского выражения completely sinus, т. е. “дополнительный синус” (или иначе “синус дополнительной дуги”; cosa =  sin( 90° - a)).

Тангенсы возникли в связи с решением задачи об определении длины тени. Тангенс (а также котангенс) введен в X веке арабским математиком Абу-ль-Вафой, который составил и первые таблицы для нахождения тангенсов и котангенсов. Однако эти открытия долгое время оставались неизвестными европейским ученым, и тангенсы были заново открыты лишь в XIV веке немецким математиком, астрономом Регимонтаном (1467 г.). Он доказал теорему тангенсов.  Региомонтан составил также подробные тригонометрические таблицы; благодаря его трудам плоская и сферическая тригонометрия стала самостоятельной дисциплиной и в Европе.

Название «тангенс», происходящее от латинского tanger (касаться), появилось в 1583 г.  Tangens переводится как «касающийся» (линия тангенсов – касательная к единичной окружности).

Региомонтан

Дальнейшее развитие тригонометрия получила в трудах выдающихся астрономов Николая Коперника (1473-1543) – творца гелиоцентрической системы мира, Тихо Браге (1546-1601) и Иогана Кеплера (1571-1630), а также в работах математика Франсуа Виета (1540-1603), который полностью решил задачу об определениях всех элементов плоского или сферического треугольника по трем данным.

Николай Коперник Тихо Браг Иоган Кеплер

Долгое время тригонометрия носила чисто геометрический характер, т. е. Факты, которые мы сейчас формулируем в терминах тригонометрических функций, формулировались и доказывались с помощью геометрических понятий и утверждений. Такою она была еще в средние века, хотя иногда в ней использовались и аналитические методы, особенно после появления логарифмов. Пожалуй, наибольшие стимулы к развитию тригонометрии возникали в связи с решением задач астрономии, что представляло большой практический интерес (например, для решения задач определения местонахождения судна, предсказания затемнения и т. д.). Астрономов интересовали соотношения между сторонами и углами сферических треугольников. И надо заметить, что математики древности удачно справлялись с поставленными задачами.

Начиная с XVII в., тригонометрические функции начали применять к решению уравнений, задач механики, оптики, электричества, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, для изучения переменного электрического тока и т. д. Поэтому тригонометрические функции всесторонне и глубоко исследовались, и приобрели важное значение для всей математики.

Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком XVIII веке Леонардом Эйлером (1707-1783) членом Петербургской Академии наук. Громадное научное наследие Эйлера включает блестящие результаты, относящиеся к математическому анализу, геометрии, теории чисел, механике и другим приложениям математики. Именно Эйлер первым ввел известные определения тригонометрических функций, стал рассматривать функции произвольного угла, получил формулы приведения. После Эйлера тригонометрия приобрела форму исчисления: различные факты стали доказываться путем формального применения формул тригонометрии, доказательства стали намного компактнее проще,

Таким образом, тригонометрия, возникшая как наука о решении треугольников, со временем развилась и в науку о тригонометрических функциях.

Позднее часть тригонометрии, которая изучает свойства тригонометрических функций и зависимости между ними, начали называть гониометрией (в переводе – наука об измерении углов, от греческого gwnia - угол,  metrew- измеряю). Термин гониометрия в последнее время практически не употребляется.

Основные тригонометрические тождества.

Тригонометрические выражения.

В геометрии угол определяется как часть плоскости, ограниченная двумя лучами. При таком определении получаются углы от 0° до 180°. Однако угол можно рассматривать и как меру поворота. Возьмем на координатной плоскости окружность радиуса R с центром O в начале координат. Пусть одна сторона угла ? с вершиной в начале координат O идёт по оси абсцисс, а сам угол положительный, то есть, по определению, отложен по направлению против часовой стрелки от положительного направления оси абсцисс. Из геометрии известно, что отношение длины дуги l , на которую опирается этот угол, к радиусу R этой окружности не зависит от самого радиуса. Поэтому это отношение может быть выбрано характеристикой и мерой данного угла:

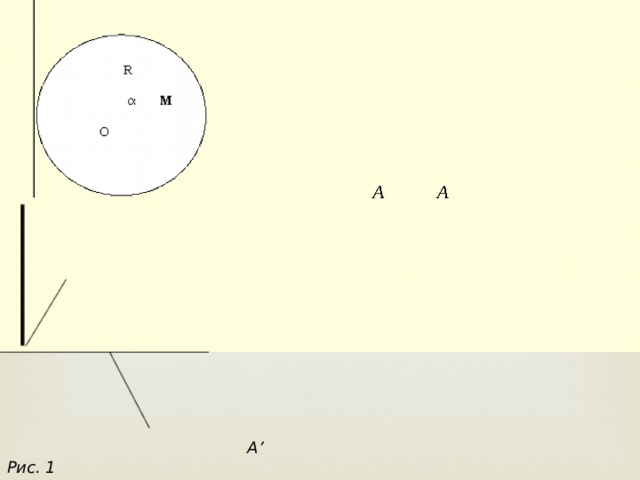
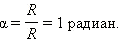Такая мера называется радианной мерой угла и используется наравне с угловой. Говорят, что угол равен определённому числу радиан. Ясно, что угол в один радиан опирается на длину дуги окружности, равную её радиусу. В самом деле: Обозначение радиана – «рад». Так как длина всей окружности радиуса R равна 2? R , то всей окружности соответствует угол радиан. Поскольку вся окружность содержит 360°, то один радиан соответствует градусов:

И наоборот,

Значит, можно написать следующие формулы перехода от градусного измерения к радианному:

и от радианного измерения к градусному:

Обозначение «рад» при записи часто опускают и вместо, например, 180° = ? рад пишут просто 180° = ?.

Пользуясь этими формулами, легко получить следующую таблицу перевода некоторых наиболее часто встречающихся углов из градусной меры в радианную и обратно.

Формулы приведения.

Формулы приведения

Эти формулы позволяют:

1)  найти численные значения тригонометрических функций углов, больших 90°;

2)  выполнить преобразования, приводящие к более простым выражениям;

3)  избавиться от отрицательных углов и углов, больших 360°.

Решение прямоугольных треугольников

По двум сторонам. По стороне и острому углу.

Обратные тригонометрические функции

Определения. Многозначность и главные значения

обратных тригонометрических функций.

Соотношение x = sin y  позволяет найти как  x  по заданному  y, так и  y  по заданному x ( при | x | 1 ). Таким образом, можно рассматривать не только синус как функцию угла, но и угол – как функцию синуса. Этот факт может быть записан как:  y = arcsin x ( “arcsin” читается “арксинус” ). Например, вместо 1/2 = sin 30 можно записать: 30arcsin 1/2. При второй форме записи угол обычно представляется в радианах:  6  = arcsin 1/2.

Определения. arcsin x – это угол, синус которого равен  x. Аналогично определяются функции arccos x, arctan x, arccot x, arcsec x, arccosec x. Эти функции являются обратными по отношению к функциям  sin x, cos x, tan x, cot x, sec x, cosec x, поэтому они называются обратными тригонометрическими функциями. Все обратные тригонометрические функции являются многозначными функциями, то есть каждому значению аргумента соответствует бесчисленное множество значений функции. Так, например, углы 30, 150, 390 510750имеют один и тот же синус.

Главное значение arcsin x – это его значение, которое находится между  2  и  + 2  (  90 и  + 90 ), включая границы:

– / 2    arcsin x    + / 2 . 

Главное значение arccos x – это его значение, которое находится между 0  и    ( 0 и  + 180 ), включая границы:

  0    arccos x    .

Главное значение arctan x – это его значение, которое находится между  2  и  + 2  (  90 и + 90 ) без границ:

– / 2  x  / 2 .