
АЛГЕБРА ЛОГИКИ
ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ И АЛГЕБРЫ ЛОГИКИ

Ключевые слова
- логическое высказывание
- логическая операция
- логическая переменная
- предикат

Алгебра логики
Алгебра логики – раздел математики, изучающий высказывания, рассматриваемые с точки зрения их логических значений (истинности или ложности), и логические операции над ними.
!
Джордж Буль (1815-1864) – английский математик, основоположник алгебры логики. Изучал логику мышления матема-тическими методами и разработал алгебраические методы решения тради-ционных логических задач. Долгое время алгебра логики была известна достаточно узкому классу специалистов.
В 1938 году Клод Шеннон применил алгебру логики для описания процесса функционирования релейно-контактных и электронно-ламповых схем.

Высказывания и переменные
Высказывание – это предложение, в отношении которого можно сказать, истинно оно или ложно.
!
Высказывания, образованные из других высказываний, называются составными . Высказывание, никакая часть которого не является высказыванием, называется элементарным .
!
Обоснование истинности или ложности элементарных высказываний не является задачей алгебры логики
Высказывания и переменные
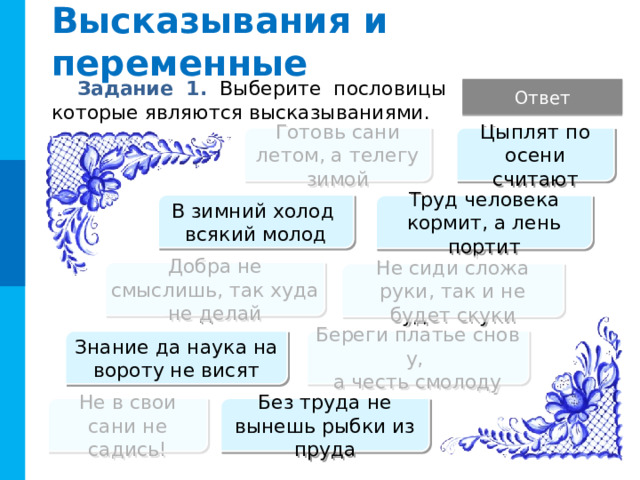
Задание 1. Выберите пословицы которые являются высказываниями.
Ответ
Готовь сани летом, а телегу зимой
Цыплят по осени считают
В зимний холод всякий молод
Труд человека кормит, а лень портит
Добра не смыслишь, так худа не делай
Не сиди сложа руки, так и не будет скуки
Комментарий
Фразеологизмы с глаголами в повелительном наклонении не являются высказываниями, так же как и вопросительные предложения.
Береги платье снову, а честь смолоду
Знание да наука на вороту не висят
Не в свои сани не садись!
Без труда не вынешь рыбки из пруда
Высказывания и переменные
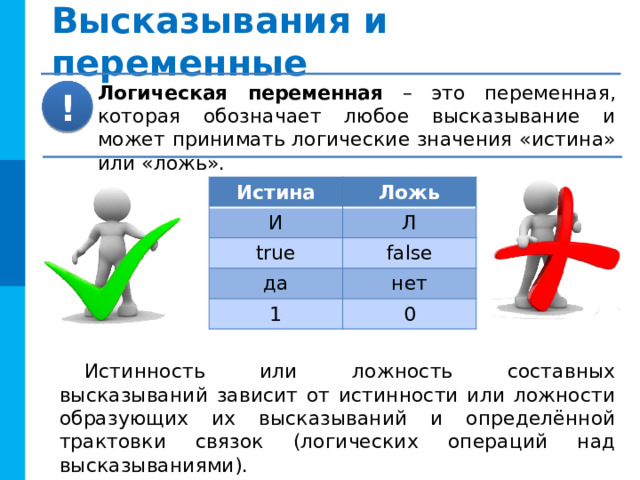
Логическая переменная – это переменная, которая обозначает любое высказывание и может принимать логические значения «истина» или «ложь».
!
Истина
И
Ложь
Л
true
false
да
нет
1
0
Истинность или ложность составных высказываний зависит от истинности или ложности образующих их высказываний и определённой трактовки связок (логических операций над высказываниями).
Логическое
Логическое
умножение
сложение
Логические операции
Дизъюнкция
Конъюнкция
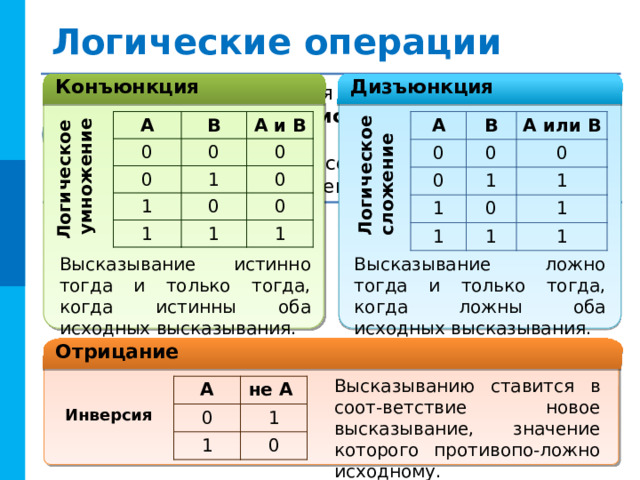
Логическая операция полностью может быть описана таблицей истинности , указывающей, какие значения принимает составное высказывание при всех возможных значениях образующих его элементарных высказываний.
!
A
B
0
0
0
A или B
1
1
0
1
0
1
1
1
1
A
B
0
0
A и B
0
1
0
1
0
1
0
1
0
1
Высказывание ложно тогда и только тогда, когда ложны оба исходных высказывания.
Высказывание истинно тогда и только тогда, когда истинны оба исходных высказывания.
Комментарий : Анимация по пробелу.
Отрицание
Высказыванию ставится в соот-ветствие новое высказывание, значение которого противопо-ложно исходному.
A
0
не A
1
1
0
Инверсия

Логические операции
Пример высказывания :
Если верно списали пример, то получили верный ответ.
Импликация
Следование
A
B
0
A → B
0
0
1
1
1
1
0
1
1
0
1
A: Пример списали верно
B: Получили верный ответ
В высказывании нет информации о правильности самого решения. Анализи-ровать можно только то, что сказано в высказывании.
Если списали неверно, то ответ может быть любым.
Из ложной посылки можно получить истинное и ложное высказывание, из истинного только истинное.
Ложно тогда и только тогда, когда посылка (первое) истинна, а следствие (второе) ложно.
Комментарий : Анимация по пробелу.
Логические операции
Пример высказывания :
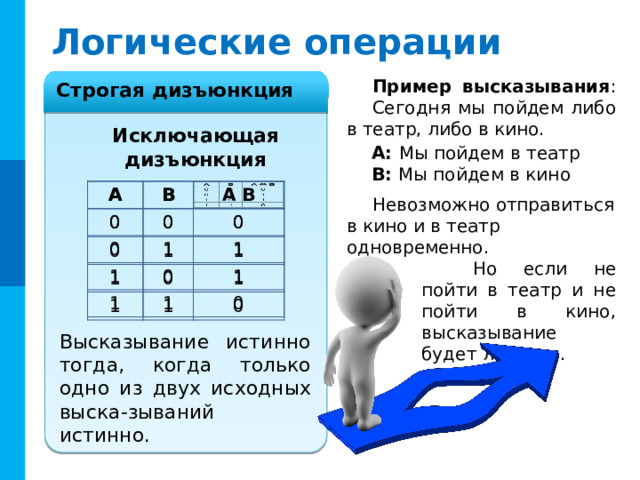
Сегодня мы пойдем либо в театр, либо в кино.
Строгая дизъюнкция
Исключающая дизъюнкция
A: Мы пойдем в театр
B: Мы пойдем в кино
A
A
B
B
0
0
0
0
A B
0
0
1
1
1
0
0
1
1
1
0
1
1
0
1
1
1
1
0
0
Невозможно отправиться в кино и в театр одновременно.
Но если не пойти в театр и не пойти в кино, высказывание будет ложным.
Комментарий : Анимация по пробелу.
Высказывание истинно тогда, когда только одно из двух исходных выска-зываний истинно.

Логические операции
Пример высказывания :
Аттестат об образовании выдается тогда и только тогда, когда выпускник успешно про-ходит государственную итоговую аттестацию.
Эквиваленция
Равнозначность
A
B
0
A ↔ B
0
0
1
1
1
1
0
0
1
0
1
A: Выдается аттестат
B: Успешное прохождение аттестации
Два события взаимо-связаны. Получение аттестата без успешного прохождения процедуры ЕГЭ невозможно, как невозможно и обратное.
Высказывание истинно тогда, когда оба исходных высказывания истинны или оба исходных выска-зывания ложны.
Комментарий : Анимация по пробелу.
Обозначения логических операций
Операция
Операция
Обозначение
Отрицание, инверсия, лог. НЕ)
Отрицание, инверсия, лог. НЕ)
Обозначение
Речевой оборот
Конъюнкция (лог. умножение, лог. И)
Конъюнкция (лог. умножение, лог. И)
Речевой оборот
,
Дизъюнкция (лог. сложение, лог. ИЛИ)
«Не», «не верно, что»
«Не», «не верно, что»
A ∧ B, A&B, A · B, AB, A и B, A and B
Дизъюнкция (лог. сложение, лог. ИЛИ)
A ∧ B, A&B, A · B, AB, A и B, A and B
A ∨ B, A + B, A | B, A ИЛИ B, A or B
Строгая дизъюнкция
«И», «как …, так и», «вместе с», «но», «хотя»
Строгая дизъюнкция
«И», «как …, так и», «вместе с», «но», «хотя»
A ∨ B, A + B, A | B, A ИЛИ B, A or B
(искл. дизъюнкция, искл. ИЛИ)
A ⊕ B, A xor B
Импликация (лог. следование)
«Или», «или …, или …,
A ⊕ B, A xor B
«Или», «или …, или …,
(искл. дизъюнкция, искл. ИЛИ)
Импликация (лог. следование)
Эквиваленция (эквивалентность, равнозначность)
A → B, A ⇒ B
или оба вместе»
«Либо …, либо», «только … или только»
«Либо …, либо», «только … или только»
или оба вместе»
A → B, A ⇒ B
Эквиваленция (эквивалентность, равнозначность)
A ↔ B, A ⇔ B,
«Если …, то», «из …
A ↔ B, A ⇔ B,
«Если …, то», «из …
«Эквивалентно», «необходимо и достаточно»
A ≡ B
«Эквивалентно», «необходимо и достаточно»
A ≡ B
следует», «влечёт»
следует», «влечёт»
Инструкция ЕГЭ
Комментарий : Анимация по пробелу.
Логические выражения
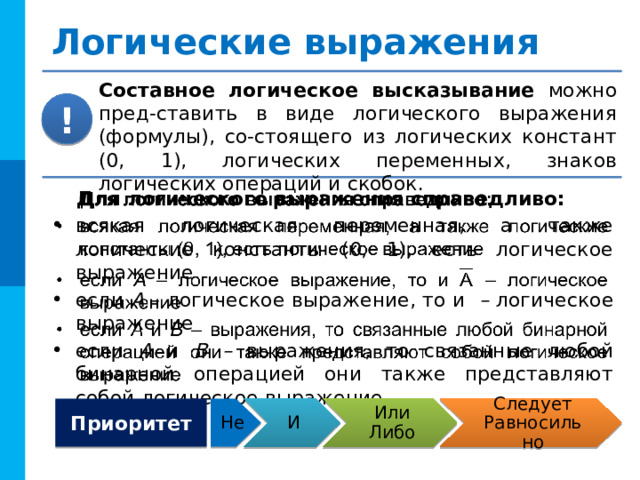
Составное логическое высказывание можно пред-ставить в виде логического выражения (формулы), со-стоящего из логических констант (0, 1), логических переменных, знаков логических операций и скобок.
!
Для логического выражения справедливо:
- всякая логическая переменная, а также логические константы (0, 1), есть логическое выражение
- если A – логическое выражение, то и – логическое выражение
- если A и B – выражения, то связанные любой бинарной операцией они также представляют собой логическое выражение
Комментарий : Анимация по пробелу.
Не
И
Или Либо
Следует Равносильно
Приоритет
12
Логические выражения
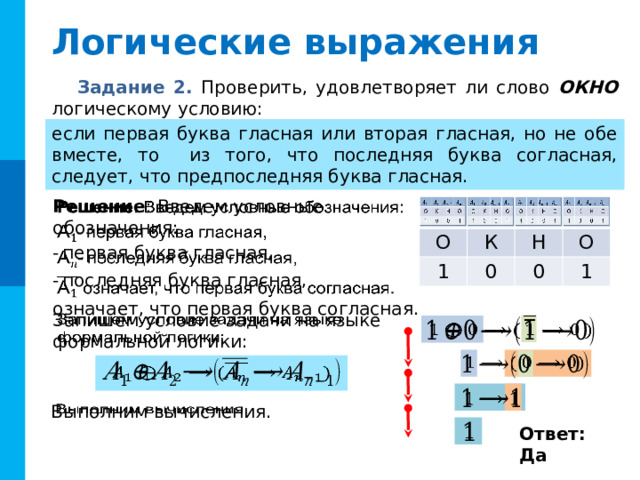
Задание 2. Проверить, удовлетворяет ли слово ОКНО логическому условию:
если первая буква гласная или вторая гласная, но не обе вместе, то из того, что последняя буква согласная, следует, что предпоследняя буква гласная.
Решение : Введем условные обозначения:
- первая буква гласная,
- последняя буква гласная,
означает, что первая буква согласная.
О
О
К
К
1
1
0
Н
0
Н
О
О
0
0
1
1
Комментарий : Анимация по пробелу.
Запишем условие задачи на языке формальной логики:
Выполним вычисления.
Ответ: Да
Логические выражения
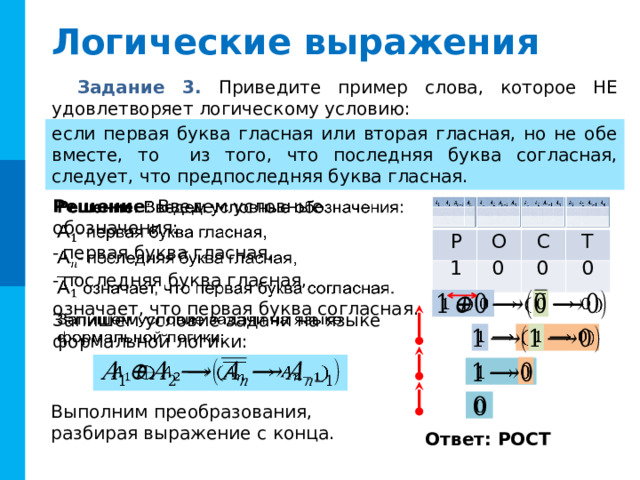
Задание 3. Приведите пример слова, которое НЕ удовлетворяет логическому условию:
если первая буква гласная или вторая гласная, но не обе вместе, то из того, что последняя буква согласная, следует, что предпоследняя буква гласная.
Решение : Введем условные обозначения:
- первая буква гласная,
- последняя буква гласная,
означает, что первая буква согласная.
Т
С
О
Р
0
1
0
0
Комментарий : Анимация по пробелу.
Решение задачи с конца.
Запишем условие задачи на языке формальной логики:
Выполним преобразования, разбирая выражение с конца.
Ответ: РОСТ
Логические выражения
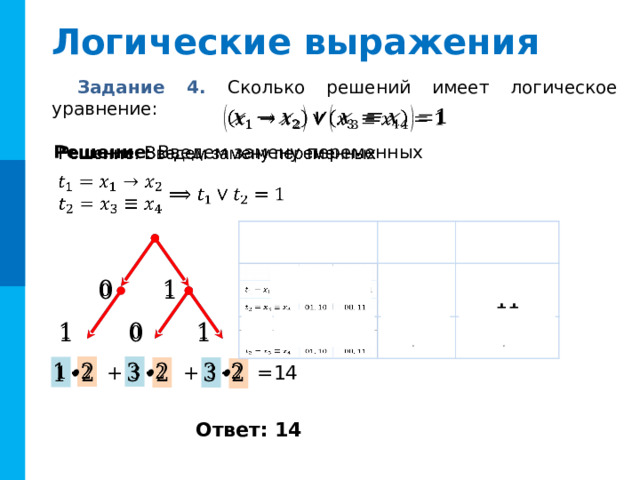
Задание 4. Сколько решений имеет логическое уравнение:
Решение : Введем замену переменных
0
0
1
10
10
1
00, 01, 11
00, 01, 11
01, 10
01, 10
00, 11
00, 11
Комментарий : Анимация по пробелу.
=14
+
+
Ответ: 14

Предикаты и множества истинности
Предикат – это утверждение, содержащее одну или несколько переменных.
!
Предикаты позволяют задать множество, не перечисляя всех его элементов.
Предикат описывает множество отрицательных чисел.
Какое множество на координатной плоскости задает предикат ?
Комментарий : Анимация по пробелу. Ответ на вопрос появляется после выбора кнопки «Ответ»
Ответ
16

1. У: п.18 2. У: №1,№3, №4(1-5), ;6(1,2)
Домашнее задание

https:// onlinetestpad.com/hmaig5gsd3si4

Самое главное
Высказывание – это предложение, в отношении которого можно сказать, истинно оно или ложно. Высказывания, образованные из других высказываний, называются составными. Высказывание, никакая часть которого не является высказыванием, называется элементарным.
Истинность или ложность составных высказываний зависит от истинности или ложности образующих их высказываний и логических операций над высказываниями.
Логическая операция полностью может быть описана таблицей истинности, указывающей, какие значения принимает составное высказывание при всех возможных значениях образующих его элементарных высказываний.

Самое главное
0
0
1
1
1
1
0
0
0
0
0
0
0
0
1
0
1
0
1
1
0
0
0
0
1
0
1
0
1
1
1
1
1
1
0
0
1
0
0
1
1
1
1
1
1
1
1
1
1
0
1
0
0
0
1
1
1
1
0
0
0
0
1
1
Приоритет операций: отрицание; конъюнкция; дизъюнкция и строгая дизъюнкция; импликация и эквиваленция.
Операции одного приоритета выполняются в порядке их следования, слева направо. Скобки меняют порядок выполнения операций.
Предикат – это утверждение, содержащее одну или несколько переменных. Из имеющихся предикатов с помощью логических операций можно строить новые предикаты.

Вопросы и задания
- Выбрать два противоположных высказывания:
- Среди учеников деревни Сосновка только один добирается до школы на автобусе
- Все ученики деревни Сосновка добираются до школы на автобусе
- Никто из учеников деревни Сосновка не добирается до школы на автобусе
- В деревне Сосновка есть хотя бы один ученик, который до школы добирается не на автобусе
Ответ
Комментарий : Ответы появляются после выбора соответствующей кнопки.
Ответ

Вопросы и задания
- Сколько точек с целочисленными координатами удовлетворяют условию:
Решение
Ответ: 1
Комментарий : Ответы появляются после выбора соответствующей кнопки.
- Сколько решений имеет логическое уравнение :
Ответ
Ответ: 12

Информационные источники
- https://upload.wikimedia.org/wikipedia/commons/thumb/6/6c/George_Boole.jpg/267px-George_Boole.jpg
- http://start2finish.org/wp-content/uploads/2015/02/photodune-9850340-symbol-s.jpg
- http://i.piccy.info/i7/c329fe9c30f528069f625349057186a0/1-2-550/47021940/013_010.jpg
- http://i.мастерская-психолога.рф/u/70/9dbf66933a11e3a4cc8e8087cd4527/-/%D0%B2%D1%8B%D0%B1%D0%BE%D1%80%20%D0%BF%D1%83%D1%82%D0%B8.jpg
- http://www.thegameengineer.com/blog/wp-content/uploads/2014/02/dreamstime_s_21174065.jpg
















































