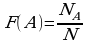Урок по математике в 8 классе на тему «Определение вероятности. Вероятность случайного события»
учитель математики МБОУ Полненской СОШ
Алексикова Алина Олеговна
Тип урока: урок применения знаний и умений учащихся, получения новых знаний.
Цели урока:
Обучающие:
повторить навыки применения формулы для нахождения вероятности событии и научить применять её в задачах;
проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать логически некорректные рассуждения.
Развивающие:
развить навыки поиска, обработки и представления информации;
развить умение сравнивать, анализировать, делать выводы;
развить наблюдательность, а также коммуникативные умения.
Воспитательные:
воспитать внимательность, усидчивость;
сформировать понимание значимости математики как способа познания окружающего мира.
Оборудование: раздаточный материал, презентация, игральные кубики (2 шт)
Ход урока.Мотивация. (3 мин)
-Здравствуйте,дети.Сегодня я хотела бы начать урок вот с такого отрывка:
2.Организационный момент. (4 мин)
- Ребята, на предыдущем уроке с каким новым понятием мы познакомились? (Определение вероятности)
- Верно. Мы с вами разобрали и записали, что такое вероятность и узнали, что для нее есть классическая формула.
Давайте же вспомним, что такое вероятность
В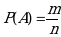 ероятностью Р наступления случайного события А называется отношение m к n, где n – это число всех возможных исходов эксперимента, а m – это число всех благоприятных исходов.
ероятностью Р наступления случайного события А называется отношение m к n, где n – это число всех возможных исходов эксперимента, а m – это число всех благоприятных исходов.
- Формула представляет собой так называемое классическое определение вероятности по Лапласу, пришедшее из области азартных игр, где теория вероятностей применялась для определения перспективы выигрыша. Эта формула применяется для опытов с конечным числом равновозможных исходов.
Вероятность события = 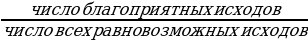
Таким образом, вероятность – это число от 0 до 1.
Вероятность равна 0, если событие невозможное.
Вероятность равна 1, если событие достоверное.
-Решим задачу устно: На книжной полке стоят 20 книг, из них 3 справочника. Какова вероятность, что взятая с полки книга не окажется справочником?
Решение:
Общее число равновозможных исходов – 20
Число благоприятных исходов – 20 – 3 = 17
Р =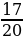 = 0,85.
= 0,85.
Ответ: 0,85.
-Были ли у вас вопросы при решении домашнего задания? Тогда продолжим дальше.
3.Актуализация опорных знаний. (5 мин)
-Сколько видов событий мы с вами выделили на прошлом уроке? (Два. Достоверное и случайное)
- Внимание на экран, перед вами ряд событий. Нам надо распределить их по известным видам.
-Хорошо,молодцы!
- Два события мы были вынуждены пропустить. Почему? (не смогли эти события отнести ни к достоверным, ни к случайным)
- Как бы мы могли назвать эти события? ( Нереальные, не происходящие, несуществующие, невозможные)
-Давайте повторим, какие же виды событий существуют?
1. Событие, которое обязательно наступит, называется достоверным.
2. Событие, которое никогда не наступит, называется невозможным.
3. Событие, которое может, как наступить, так и не наступить, называется случайным.
4. Любой результат испытания называется исход.
4. Объяснение нового материала. (17 мин)
А можно ли вычислить вероятность события с помощью ряда экспериментов? (можно)
-Но для начала нам необходимо познакомиться с таким понятием, как частота случайного события
Частота случайного события.
Относительной частотой случайного события называют отношение числа появлений этого события к общему числу проведенных экспериментов:
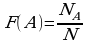
где А – случайное событие по отношению к некоторому испытанию
N раз проведено испытание и при этом событие А наступило в NA случаях.
- Зная формулу и определение частоты случайного события давайте проведем опыт. Предлагаю вам вернуться на несколько столетий назад и повторить их эксперимент.
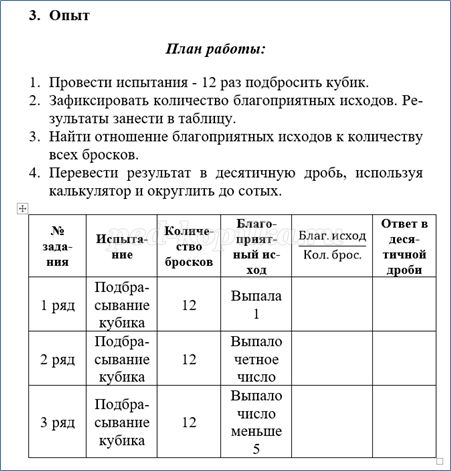
Эксперимент с игральным кубиком. Работа в парах.
1 ряд проводит 1 эксперимент, 2 ряд – 2 эксперимент. План работы на экране презентации и в тетради на печатной основе. Закончив эксперимент запишите ваш результат на доске, там, где записан номер вашего ряда.
- Точно такой же эксперимент французский ученый Жорж Бюффон. Но он не был ограничен временем урока и сделал это 4040 раз. В ходе эксперимента у Бюффона герб выпал 2048 раз. Как найти какую часть от всех исходов составляет исход «выпал герб»? Произведите расчет с помощью калькулятора, округлите до десятых и ответьте, чему равна частота события «выпадения герба».
Ответ: Найдем отношение 2048 к 4040. После округления получили 0,5. Следовательно, частота события «выпал герб» в данном эксперименте равна 0,5.
- Английский математик Карл Пирсон в начале двадцатого столетия провел такой же эксперимент. Он подбрасывал монету 24000 раз. Пирсон считал сколько раз выпадет решка. В ходе эксперимента он установил, что она выпала в 12012 случаях. Опираясь на то, что мы уже проанализировали результаты эксперимента Жоржа Бюффона сделайте вывод.
Ответ: Найдем отношение 1202 к 2400, округлим. Следовательно, частота события «выпадения решки» в данном эксперименте равна 0,5.
- Ребята, все завершили расчеты по эксперименту?
Запишите, пожалуйста, на доске ваши ответы.
Почему, проводя одинаковый эксперимент, получились разные ответы и такие серьезные расхождения? (провели малое количество экспериментов)
- Следовательно, чем больше испытаний, тем ближе вероятность, полученная опытным путем к действительности.
Проблемные вопросы: Удобен ли экспериментальный метод для вычисления вероятности события? Почему? Какое знание могло бы нам помочь?
Ответ: Неудобно, так как требует большого количества испытаний и много времени. При помощи формулы и алгоритма быстрее и удобнее найти вероятность.
5. Физкультминутка.(2 мин)
6. Самостоятельная работа, взаимопроверка с выводом ответов на экран (10 мин)


7. Итог урока. (4 мин)
Как вычисляют вероятность случайного события при классическом подходе?
Приведите пример достоверного события и пример невозможного события. Чему равна вероятность достоверного события; невозможного события?
8 Рефлексия
9.Домашнее задание.
Задача №1. Из 40 деталей, лежащих в ящике, 3 бракованные детали. Из ящика наугад
вынимают одну деталь. Какова вероятность того, что эта деталь окажется без
брака?
Задача №2 Ольга помнит, что телефон подруги оканчивается цифрами 5, 7, 8, но забыла, в каком порядке эти цифры следуют. Какова вероятность того, что Ольга набрала правильный номер?
Задача №3
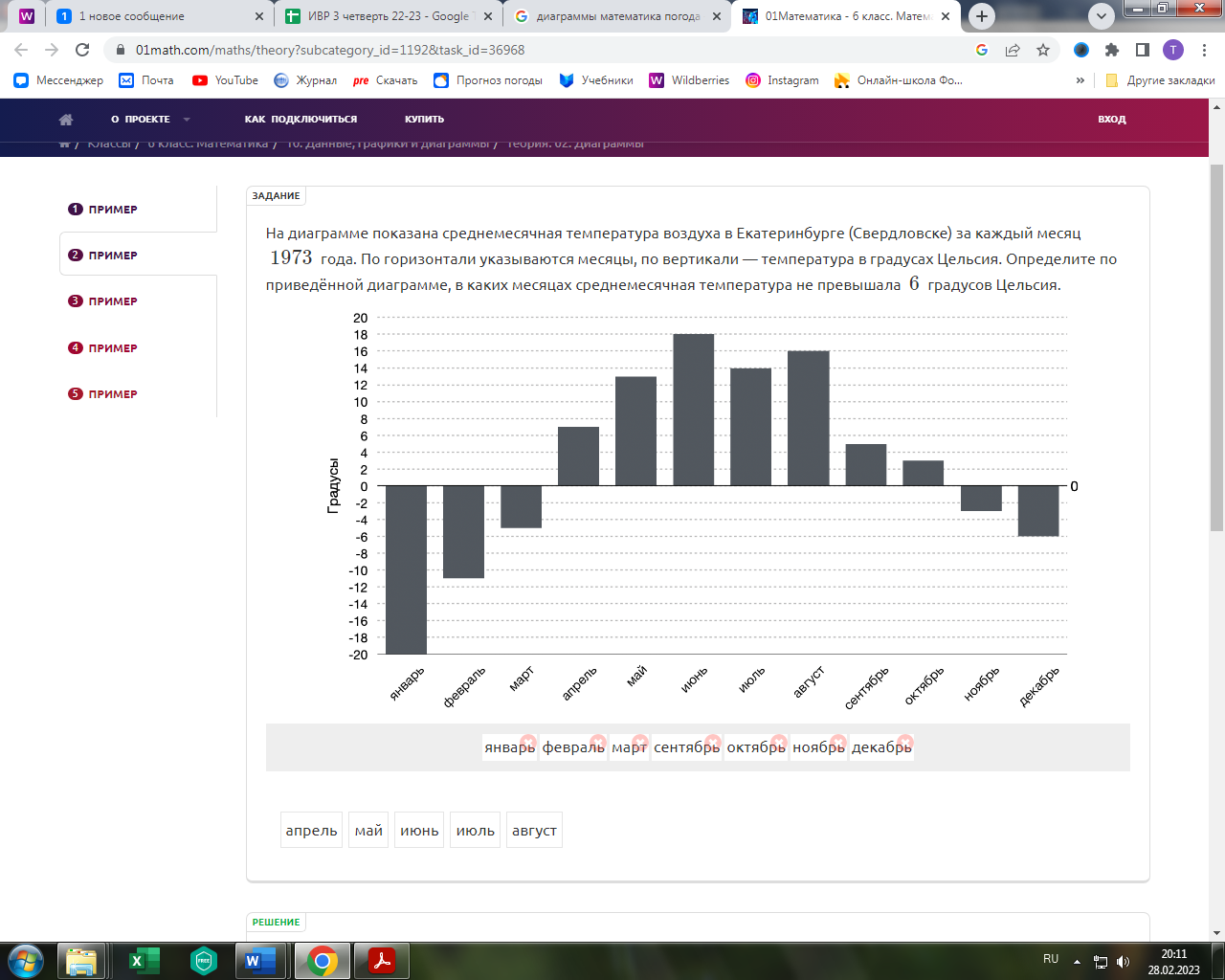
-Укажите наименьшую температуру ?
-В каком месяце температура была наибольшей ?
-Сколько месяцев температура не превышала +10 ?
-Найти разницу между температурой в августе с температурой в январе
-В какие месяцы температура была отрицательной ?







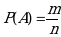 ероятностью Р наступления случайного события А называется отношение m к n, где n – это число всех возможных исходов эксперимента, а m – это число всех благоприятных исходов.
ероятностью Р наступления случайного события А называется отношение m к n, где n – это число всех возможных исходов эксперимента, а m – это число всех благоприятных исходов.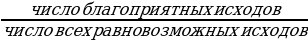
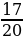 = 0,85.
= 0,85.