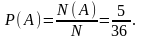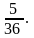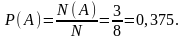Тема урока: «Простейшие вероятностные задачи».
Предмет: математика
Автор урока: Ельникова Светлана Николаеевна
Тип урока: комбинированный.
Длительность: 1 учебный час.
Цель урока: Дать определение вероятности. Научиться вычислять вероятности различных видов событий. Применять знания для решения задач.
Планируемые образовательные результаты:
1) личностные: формировать умения
работать в коллективе, парах;
находить согласованные решения;
самоконтроля и самостоятельного исправления ошибок;
2) метапредметные: формировать умения самостоятельно
планировать свои действия в соответствии с учебным заданием;
ставить цели;
выбирать и создавать алгоритмы решения учебных математических задач;
3)предметные:
сформировать представления о процессах и явлениях, имеющих вероятностный характер в реальном мире, об основных понятиях элементарной теории вероятностей;
научить в процессе реальной ситуации определять термины теории вероятностей: достоверные, невозможные, равновозможные, противоположные события;
научить находить вероятности случайного события с очевидными благоприятствующими исходами; вероятности противоположного события;
научить решать простейшие текстовые задачи на расчет вероятности случайного события;
развить основные навыки и умения использования компьютерных устройств.
Основные виды учебной деятельности (на уровне учебных действий): учащийся научится:
в процессе реальной ситуации определять достоверные, невозможные, равновероятностные, совместные и несовместные события;
распознавать логически некорректные рассуждения;
находить вероятности случайных событий с помощью классического определения вероятности;
находить вероятность противоположного события;
интуитивно определять независимые события и находить вероятность одновременного наступления независимых событий в задачах;
использовать приобретенные знания и умения для сравнения шансов наступления случайных событий, для оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией.
Форма урока отличается от уроков в традиционном обучении. Ученики не сидят пассивно, слушая учителя, а становятся главными действующими лицами урока. Роль учителя — в основном координирующая.
Используемые технологии: развивающее обучение, групповая технология, ИКТ, элементы исследовательской деятельности, элементы блочного изучения тем.
Оборудование и материалы для урока: компьютер, проектор, презентация по теме «Простейшие вероятностные задачи», экран.
План урока:
1) Организационный момент.
2 Актуализация знаний. Создание мотивации.
3) Изучение нового материала.
4) Решение простейших вероятностных задач.
4) Итоги урока.
5) Домашнее задание.
Ход урока
1. Организационный момент (3 мин)
Приветствие учеников.
Наша жизнь наполнена событиями. Они бывают счастливые и не очень, происходящие с нами или с другими людьми? И всем интересно знать, что же произойдёт, что же ждёт нас впереди. С древних времён люди занимались предсказаниями. Ходили к гадалкам и шаманам, составляли гороскопы. А как же ученые математики, с их рациональным мышлением могли ли они пройти мимо такой темы?
Мало им стало рациональных чисел, придумали они дроби, мало дробей- придумали отрицательные числа, потом корни. Всё они пытаются описать графиком, заключить в формулу. А тут….Случай, случайность — с ними мы встречаемся повседневно: случайная встреча, случайная поломка, случайная находки, случайная ошибка. Казалось бы, тут нет места для математики—какие уж законы в царстве Случая! Но и здесь наука обнаружила интересные закономерности—они позволяют человеку уверенно чувствовать себя при встреча со случайными событиями, прогнозировать наступление того или иного события, подсчитывая его вероятность.
Как Вы думаете какова тема нашего сегодняшнего урока? (Чем же мы будем заниматься на уроке- предсказывать события, вычислять события, т.е давать числовую характеристику тем или иным событиям- теория вероятности)
Сообщение темы и цели урока.
А первым вашим предсказателем (Нострадамусом ) буду я, и сейчас я прошу вас выбрать одну из фигур на экране и никому о ней не говорить. А что всё это значит, все мои предсказания в конце урока. А пока как истинные математики мы с вами начнём выстраивать кирпичики знаний.
3. Изучение нового материала
Если бы Вы писали научную работу и Вам было нужно дать определение события, то …(формулировка детей)
(В теории вероятностей под событием понимают то, относительно чего после некоторого момента времени можно сказать одно и только одно из двух. Да, оно произошло. Нет, оно не произошло.)
Случайное событие_( Непредсказуемые события называются случайными. )
Теория вероятностей — наука о вычислении вероятностей случайных событий. Основной объект изучения теории вероятностей: - случайное событие и его вероятность;
Например:
В следующем году первый снег выпадет в субботу. Бутерброд упадет маслом вниз. При бросании кубика выпадет шестерка. При бросании кубика выпадет четное число.
Теория вероятностей изучает различные модели случайных событий, их свойства и характеристики. Разумеется, эта теория не может однозначно предсказать, какое событие в реальности произойдет, но может оценить, какое событие наиболее вероятно.
Равновозможные и неравновозможные события. (называются события, когда в их наступлении нет преимуществ, события те, у которых в наступлении одного из событий есть какое то преимущество.)
Совместные и несовместные события. (Два события, которые в данных условиях могут происходить одновременно, называются совместными, а те, которые не могут происходить одновременно, - несовместными. )
Достоверные события. (Событие, которое происходит всегда. Вероятность достоверного события равна 1)
Невозможные события. (Событие, которое не может произойти, называется невозможным. Вероятность невозможного события равна 0.)
События А и В называются противоположными, если всякое наступление события А означает ненаступление события В, а ненаступление события А – наступление события В.
Вероятность события-– это численная характеристика реальности появления того или иного события. Случайное (0,1) Невозможное-0, Достоверное-1
Примеры. (к каким событиям можно отнести)
Из ящика с деталями наудачу извлечена деталь.
Появление стандартной детали исключает появление нестандартной детали. События «появилась стандартная деталь» и «появилась нестандартная деталь» - несовместные.
Брошена монета.
Появление «герба» исключает появление надписи. События «появился герб» и «появилась надпись» - несовместные. Появление герба или надписи при бросании монеты представляют собой равновероятные события.
Пусть бросают игральную кость.
В силу симметрии кубика можно считать, что появление любой из цифр 1, 2, 3, 4, 5 или 6 одинаково возможно (равновероятно).
При бросании кубика выпадет семерка.
Это невозможные события.
5. Пусть, например, из урны, содержащей только черные шары, вынимают шар. Тогда появление черного шара – достоверное событие; появление белого шара – невозможное событие.
ПРИДУМАЙТЕ СОБЫТИЕ (одноклассники отгадывают)
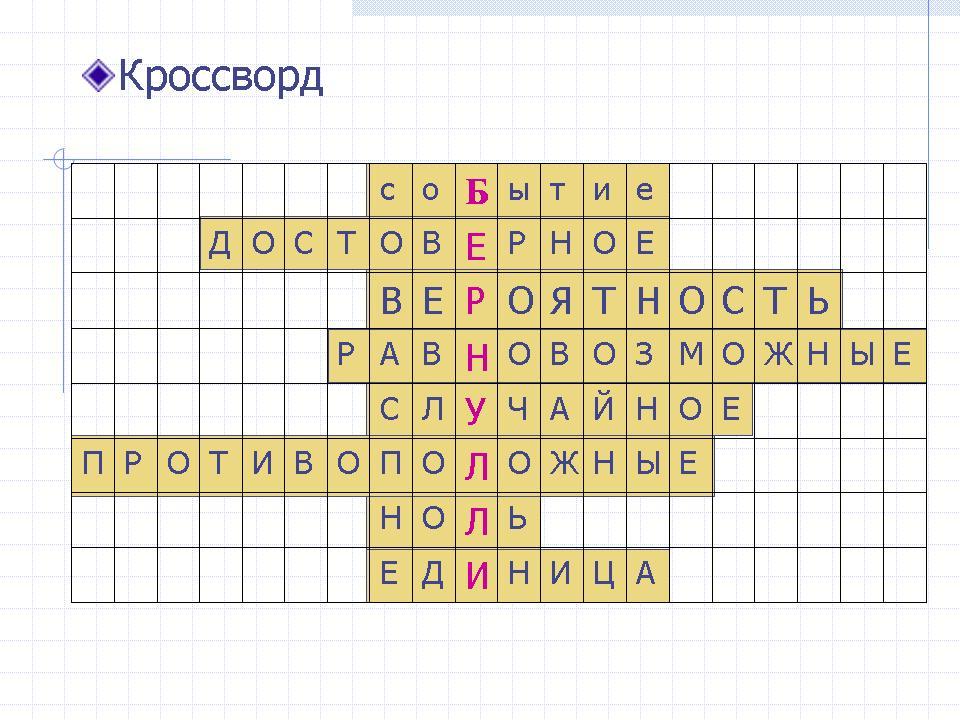
КРОССВОРД
Разгадав кроссворд, мы узнаем, кто из математиков придумал и впервые опубликовал классическую вероятностную схему.
Вопросы кроссворда:
результат испытания.
событие, которое происходит всегда.
численная характеристика реальности появления того или иного события.
события, в наступлении которых нет преимуществ.
непредсказуемое событие.
всякое наступление события А означает ненаступление события В.
вероятность невозможного события.
вероятность достоверного события.
Исторический экскурс. ( Доклад обучающегося)
Теория вероятностей – раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними. (Советский энциклопедический словарь, 1982 год)
История теории вероятностей отмечена уникальными особенностями. Прежде всего, у теории вероятностей не было античных или средневековых предшественников, это «молодая» наука. Первые работы, в которых зарождались основные понятия теории вероятностей, представляли собой попытки создания теории азартных игр (Кардано, Гюйгенс, Паскаль, Ферма и другие в XVI—XVII вв).
Долгое время теория вероятностей считалась чисто опытной наукой и «не совсем математикой», потому, что в начале это были лишь курьёзные задачки, связанные с играми в кости и в карты.
А вот в XVII веке уже теория вероятностей нашла своё применение в демографии, страховом деле, в оценке ошибок наблюдения. Над этими вопросами и работали основатели теории вероятностей французские математики Б. Паскаль, П. Ферма, голландский учёный Х. Гюйгенс.
В XVIII веке появились книга Я. Бернулли (швейцарский математик. Один из основателей теории вероятностей и математического анализа. ) «Искусство предположений» (1713 год). В ней Бернулли предложил классическое определение вероятности случайного события как отношение числа равновероятных исходов, связанных с этим событием, к общему числу исходов. Он также изложил «закон больших чисел» и мн.др.
Наиболее плодотворный период связан с именами П.Л. Чебышева (1821 – 1894 гг.) и его учениками А.А. Маркова (1856 – 1922 гг.) и А.М. Ляпунова (1857 – 1918 гг.). В этот период теория вероятностей становится стройной математической наукой.
К концу XIX века появляются статистическая физика, строгая теория ошибок измерения.
В XX веке в физике была создана теория микромира, а в биологии — теория наследственности, обе они основаны на вероятностных методах.
Что такое «теория вероятностей»? В наши дни теория вероятностей занимает одно из первых мест в прикладных науках.
А нашла ли своё отражение теория вероятностей в вариантах ГИА?
Поэтому цель нашего урока не просто научиться решать простейшие вероятностные задачи, но и подготовиться к выполнению этого задания на экзамене.
Классическое определение вероятности.
Вероятностью события А при проведении некоторого испытания называют отношение числа тех исходов, в результате которых наступает событие А, к общему числу всех (равновозможных между собой) исходов этого испытания.
Для решения задач используют алгоритм нахождения вероятности случайного события. (слайд 9)
Для нахождения вероятности случайного события А при проведении некоторого испытания следует найти:
число N всех возможных исходов данного испытания;
количество N(A) тех исходов, в которых наступает событие А;
частное 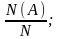 оно и будет равно вероятности события А.
оно и будет равно вероятности события А.
Принято вероятность события А обозначать так: Р(А). Значит Р(А) = 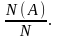
По элементам теории вероятностей также целесообразно иметь опорный конспект:
| Основные понятия |
| понятие | определение | вероятность |
| Случайное событие | Событие, которое может произойти или не произойти при проведении опыта | 0 ≤ Р (А) ≤ 1 |
| Достоверное событие | Событие, которое происходит при проведении опыта всегда | Р(А) = 1 |
| Невозможное событие | Событие, которое не может произойти ни при каком исходе опыта | Р(А) = 0 |
| Равновозможные событие | События, которые имеют равные возможности произойти | 0 ≤ Р (А) ≤ 1 |
| Противоположными событие | События А и В называются противоположными, если всякое наступление события А означает ненаступление события В, а ненаступление события А – наступление события В. | Р(А) = 1- Р(В) |
| Нахождение вероятности | Для нахождения вероятности случайного события А при проведении некоторого испытания следует найти: число N всех возможных исходов данного испытания; количество N(A) тех исходов, в которых наступает событие А; частное 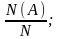 оно и будет равно вероятности события А. оно и будет равно вероятности события А.
| Р(А) =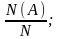 |
Решение задач
Какое событие произошло 59 лет назад? (полёт человека в космос)
Можно ли это событие назвать случайным (да)
Устные задачи про космос
Вселенная с ее загадочными и непредсказуемыми просторами интересует человечество на протяжении всей жизни. Исследования, проводимые в космосе, открывают постепенно завесу космических тайн, но, сколько их еще осталось не изученных.
Гагарин был очарован видом, который он увидел сквозь иллюминатор. Он увидел красоту нашей планеты и вскоре призвал людей хранить и приумножать эту красоту, а не разрушать ее!
Невооруженным глазом ночью на небе можно увидеть 6000 звезд. Звезды составляют созвездия. В созвездии Большой Медведицы 7 звезд. Найдите вероятность, что случайно увиденная звезда из этого созвездия?7/6000
Кто действительно побывал до Гагарина в космосе, так это известные всему миру собаки Белка и Стрелка, которые после трех суток полета на орбите удачно вернулись на Землю. Далеко не все эксперименты были успешны. Во время космических испытаний погибло 20 собак. Найдите вероятность удачного полёта. 1/10
Для первого полёта готовили 20 кандидатов. Какова была вероятность, что первым станет Гагарин? 1/20
Площадь всей поверхности Земли составляет 510 млн кв км, площадь поверхности суши равна 149 млн кв км ? Какова вероятность того, что обломки упадут в океан? 361/510
Примеры. (у доски) (РАЗДАТОЧНЫЙ МАТЕРИАЛ)
На завод привезли партию из 1000 подшипников. Случайно в эту партию попало 30 подшипников, не удовлетворяющих стандарту. Определить вероятность Р(А) того, что взятый наудачу подшипник окажется стандартным.
Найдем вероятность того, что при одном бросании игральной кости (кубика) выпадает: а) три очка; б) число очков, кратное трем; в) число очков больше трех; г) число очков, не кратное трем.
Найдем вероятность того, что при подбрасывании двух костей суммарное число очков окажется равным 5.
Научная конференция проводится 3 дня. Всего запланировано 50 докладов: в первый день – 30 докладов, а остальные распределены поровну между вторым и третьим днями. Порядок докладов определяется жеребьевкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Перед началом первого тура чемпионата по теннису разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 46 теннисистов, среди которых 19 участников из России, в том числе Ярослав Исаков. Найдите вероятность того, что в первом туре Ярослав Исаков будет играть с каким – либо теннисистом из России.
На завод привезли партию из 1000 подшипников. Случайно в эту партию попало 30 подшипников, не удовлетворяющих стандарту. Определить вероятность Р(А) того, что взятый наудачу подшипник окажется стандартным.
Решение. Число стандартных подшипников равно 1000 – 30 = 970. Будем считать, что каждый подшипник имеет одинаковую вероятность быть выбранным. Тогда полная группа событий состоит из N = 1000 равновероятных исходов, из которых событию А благоприятствуют N(A) = 970 исходов.
Поэтому  Р(А) =
Р(А) = 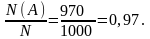
Ответ: 0,97.
2. Найдем вероятность того, что при одном бросании игральной кости (кубика) выпадает: а) три очка; б) число очков, кратное трем; в) число очков больше трех; г) число очков, не кратное трем.
Решение. Всего имеется N=6 возможных исходов: выпадение 1,2,3,4,5,6 очков. Считаем, что эти исходы равновозможны.
а) Только при одном из исходов N(А)=1 происходит интересующее нас
событие А – выпадение трех очков. Вероятность этого события 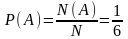 .
.
б) При двух исходах N(B) = 2 происходит событие B: выпадение числа очков кратных трем: выпадение или трех или шести очков. Вероятность такого события  .
.
в) При трех исходах N(C) = 3 происходит событие C: выпадение числа очков больше трех: выпадение четырех, пяти или шести очков. Вероятность этого события 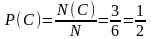 .
.
г) Из шести возможных выпавших чисел четыре (1, 2, 4 и 5) не кратны трем, а остальные два (3 и 6) делятся на три. Значит, интересующее нас событие D,
наступает в четырех случаях, т.е. N(D) = 4. Вероятность такого события: 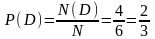 .
.
Ответ: а) 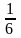 ; б)
; б) 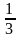 ; в)
; в) 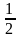 ; г)
; г) 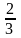 .
.
3.
Найдем вероятность того, что при подбрасывании двух костей суммарное число очков окажется равным 5.
Решение. Возможно следующее сочетание очков на первой и второй костях:
1 + 4, 2 + 3, 3 + 2, 4 + 1 – четыре благоприятных случая (N(A) = 4). Всего возможных исходов N = 6·6 = 36 (по шесть для каждой кости). Тогда вероятность рассматриваемого события 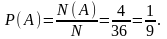
Ответ: 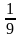 .
.
Научная конференция проводится 3 дня. Всего запланировано 50 докладов: в первый день – 30 докладов, а остальные распределены поровну между вторым и третьим днями. Порядок докладов определяется жеребьевкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Решение. Так как в третий день будут слушать 10 докладов, то благоприятных исходов N(А) = 10, а всего докладов 50, т.е. равновозможных исходов N = 50. Поэтому 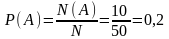 .
.
Ответ: 0,2.
5. Перед началом первого тура чемпионата по теннису разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 46 теннисистов, среди которых 19 участников из России, в том числе Ярослав Исаков. Найдите вероятность того, что в первом туре Ярослав Исаков будет играть с каким – либо теннисистом из России.
Решение. Число всех исходов N = 45. Число элементарных событий, благоприятствующих событию А равно 18. Все элементарные события равновозможны по условию задачи, поэтому 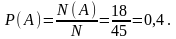
Ответ: 0,4.
(Физминутка- математическая зарядка по понятиям события)
Раздаточный материал
Решение задач ГИА (самостоятельно)
Задача 1. В фирме такси в данный момент свободно 12 машин: 3 черных, 3 желтых и 6 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.
Ответ : 0,25.
Задача 2. В случайном эксперименте симметричную монету бросают четыре раза. Найдите вероятность того, что орел выпадет ровно 2 раза.
Ответ: 0,375.
Задача 3 Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,08. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
Ответ: 0,92.
Задача 4.Определите вероятность того, что при бросании кубика выпало число очков, не меньшее 1.
Результат округлите до сотых.
Ответ: 1.
3.5. Решение задач в группах
А теперь перейдем к работе в группах. Ваша задача: решить задачи, оформить их в тетрадях и рассказать о проделанной совместной работе. Листочки с заданиями на столах. Помогайте друг другу при решении. (Преподаватель, в процессе работы обучающихся, оказывает помощь каждой группе).
Задачи лёгкого варианта. (все из сборника подготовки к ОГЭ).
В среднем на 80 карманных фонариков, поступивших в продажу, приходится 10 неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен.
На экзамене 25 билетов. Стас не выучил 5 из них. Найдите вероятность того, что ему попадётся выученный билет.
Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,12. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.
Игральную кость бросают дважды. Найдите вероятность того, что сумма двух выпавших чисел равна 5 или 8.
Коля выбирает случайное трёхзначное число. Найдите вероятность того, что оно делится на 100.
Родительский комитет закупил 20 пазлов для подарков детям в связи с окончанием года, из них 8 с машинками и 12 с видами городов. Подарки распределяются случайным образом между 20 детьми, среди которых есть Вася. Найдите вероятность того, что Васе достанется пазл с машинкой.
В фирме такси в данный момент свободно 20 машин: 4 чёрных, 6 жёлтых и 10 зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.
Задачи трудного варианта.
1. Вася, Петя, Коля и Леша бросили жребий - кому начинать игру.
Найдите вероятность того, что начинать игру должен будет Петя.
2. Игральный кубик (кость) бросили один раз. Какова вероятность того,
что выпало число очков, больше чем 4?
3. В случайном эксперименте бросают два игральных кубика.
Найдите вероятность того, что в сумме выпадет 8 очков.
4. В случайном эксперименте монету бросили три раза. Какова
вероятность того, что орел выпал ровно два раза?
5. В соревнованиях по толканию ядра участвуют 4 спортсмена из
Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции и 5-
из Норвегии. Порядок, в котором выступают спортсмены,
определяется жребием. Найдите вероятность того, что спортсмен,
который выступает последним, окажется из Швеции.
6. В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России,
7 из США, остальные – из Китая. Порядок, в котором
выступают гимнастки, определяется жребием. Найдите
вероятность того, что спортсменка, выступающая первой, окажется
из Китая.
7. Фабрика выпускает сумки. В среднем на 100 качественных
сумок приходится восемь сумок со скрытыми дефектами.
Найдите вероятность того, что купленная сумка окажется
качественной. Результат округлите до сотых.
Решения к задачам сложного варианта.
1. Случайный эксперимент – бросание жребия. Элементарное событие в этом эксперименте – участник, который выиграл жребий. Перечислим их:
(Вася), (Петя), (Коля) и (Лёша).
Общее число элементарных событий N = 4. Жребий подразумевает, что элементарные события равновозможны. Событию A = {жребий выиграл Петя}
благоприятствует только одно элементарное событие (Петя). Поэтому N(A)=1.
Тогда 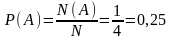 .
.
Ответ: 0,25.
2. Случайный эксперимент – бросание кубика. Элементарное событие –число на выпавшей грани. Граней всего шесть. Перечислим все элементарные события: 1,2,3,4,5 и 6. Значит, N=6. Событию A={выпало больше, чем 4} благоприятствует два элементарных события: 5 и 6. Поэтому N(A) = 2. Элементарные события равновозможны. Поэтому 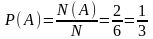 .
.
Ответ: 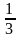 .
.
3. Элементарный исход в этом опыте – порядочная пара чисел. Первое число выпадает на первом кубике, а второе – на втором. Множество элементарных исходов удобно представить таблицей. Строки соответствуют результату первого броска, столбцы – результату второго броска. Всего элементарных событий N = 3.
1 2 3 4 5 6
| 2 | 3 | 4 | 5 | 6 | 7 |
| 3 | 4 | 5 | 6 | 7 | 8 |
| 4 | 5 | 6 | 7 | 8 | 9 |
| 5 | 6 | 7 | 8 | 9 | 10 |
| 6 | 7 | 8 | 9 | 10 | 11 |
| 7 | 8 | 9 | 10 | 11 | 12 |
1
2
3
4
5
6
Напишем в каждой клетке таблицы сумму выпавших очков и закрасим клетки где сумма равна 8. Таких ячеек 5. Значит событию А = {сумма равна 8} благоприятствует пять элементарных исходов. Следовательно, N(A) = 5.
Поэтому 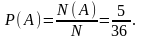
Ответ: 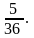
Орёл обозначим буквой О, решку – буквой Р. В описанном эксперименте элементарные исходы – тройки, составленные из букв О и Р. Выпишем все их в таблицу:
| Элементарный исход | Число орлов |
| ООО | 3 |
| ООР | 2 |
| ОРО | 2 |
| ОРР | 1 |
| РОО | 2 |
| РОР | 1 |
| РРО | 1 |
| РРР | 0 |
Всего исходов получилось 8. Значит, N=8. Событию А = {орёл выпал ровно два раза} благоприятствует элементарные события ООР, ОРО, РОО. Поэтому N(A)=3. Тогда 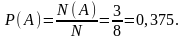
Ответ: 0,375.
5. Элементарный исход – спортсмен, который выступает последним. Последним может оказаться любой спортсмен. Всего спортсменов N=4+7+9+5+5=25. Событию А = {последний из Швеции} благоприятствуют только 9 исходов (столько, сколько участвует шведских спортсменов). Поэтому N(A)=9.
Тогда
Ответ: 0,36.
6. Элементарные события – спортсменка, выступающая первой. Поэтому N=20. Чтобы найти число элементарных событий, благоприятствующих событию А = {первой выступает спортсменка из Китая}, нужно подсчитать число спортсменок из Китая: N(A)=20-(8+7)=5. Все элементарные события равновозможны по условию задачи, поэтому
Ответ: 0,25.
7. Элементарный исход – случайно выбранная сумка. Поэтому N = 108.
Событию А = {качественная сумка} благоприятствуют 100 исходов.
Поэтому N(A) = 100.
Тогда
Ответ: 0,93.
Отчет групп о проделанной работе
(ЗАДАЧА ДАЛАМБЕРА слайды)
4. Итоги урока (слайд 20)
Обучающиеся проговаривают, что нового узнали на уроке. Учитель оценивает работу ребят. При выходе из кабинета каждый обучающийся выбирает прямоугольник по цвету, соответствующему надписями “всё понятно и усвоено”, “трудно и не всё понятно”, “не понятно и не усвоено”, и опускает в соответствующий конверт.
8. Итоги урока
Ученики проговаривают, что нового узнали на уроке. Учитель оценивает работу ребят.
9. Домашнее задание § 20; №20.8; 20.9; сборник подгот. к ОГЭ, вар.12, №1-8;
Задачи:
1. Вася, Петя, Коля и Леша бросили жребий - кому начинать игру. Найдите вероятность того, что начинать игру должен будет Петя.
2. Игральный кубик (кость) бросили один раз. Какова вероятность того, что выпало число очков, больше чем 4?
3. В случайном эксперименте бросают два игральных кубика. Найдите вероятность того, что в сумме выпадет 8 очков.
4. В случайном эксперименте монету бросили три раза. Какова вероятность того, что орел выпал ровно два раза?
5. В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции и 5- из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.
6. В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные – из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.
7. Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Решения к задачам
1. Случайный эксперимент – бросание жребия. Элементарное событие в этом эксперименте – участник, который выиграл жребий. Перечислим их:
(Вася), (Петя), (Коля) и (Лёша).
Общее число элементарных событий N = 4. Жребий подразумевает, что элементарные события равновозможны. Событию A = {жребий выиграл Петя}
благоприятствует только одно элементарное событие (Петя). Поэтому N(A)=1.
Тогда 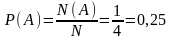 .
.
Ответ: 0,25.
2. Случайный эксперимент – бросание кубика. Элементарное событие –число на выпавшей грани. Граней всего шесть. Перечислим все элементарные события: 1,2,3,4,5 и 6. Значит, N=6. Событию A={выпало больше, чем 4} благоприятствует два элементарных события: 5 и 6. Поэтому N(A) = 2. Элементарные события равновозможны, поскольку подразумевается, что кубик честный. Поэтому 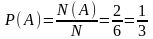 .
.
Ответ: 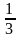 .
.
3. Элементарный исход в этом опыте – порядочная пара чисел. Первое число выпадает на первом кубике, а второе – на втором. Множество элементарных исходов удобно представить таблицей. Строки соответствуют результату первого броска, столбцы – результату второго броска. Всего элементарных событий N = 3.
1 2 3 4 5 6
| 2 | 3 | 4 | 5 | 6 | 7 |
| 3 | 4 | 5 | 6 | 7 | 8 |
| 4 | 5 | 6 | 7 | 8 | 9 |
| 5 | 6 | 7 | 8 | 9 | 10 |
| 6 | 7 | 8 | 9 | 10 | 11 |
| 7 | 8 | 9 | 10 | 11 | 12 |
1
2
3
4
5
6
Напишем в каждой клетке таблицы сумму выпавших очков и закрасим клетки где сумма равна 8. Таких ячеек 5. Значит событию А = {сумма равна 8} благоприятствует пять элементарных исходов. Следовательно, N(A) = 5.
Поэтому 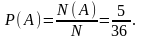
Ответ: 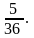
Орёл обозначим буквой О, решку – буквой Р. В описанном эксперименте элементарные исходы – тройки, составленные из букв О и Р. Выпишем все их в таблицу:
| Элементарный исход | Число орлов |
| ООО | 3 |
| ООР | 2 |
| ОРО | 2 |
| ОРР | 1 |
| РОО | 2 |
| РОР | 1 |
| РРО | 1 |
| РРР | 0 |
Всего исходов получилось 8. Значит, N=8. Событию А = {орёл выпал ровно два раза} благоприятствует элементарные события ООР, ОРО, РОО. Поэтому N(A)=3. Тогда 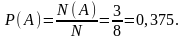
Ответ: 0,375.
5. Элементарный исход – спортсмен, который выступает последним. Последним может оказаться любой спортсмен. Всего спортсменов N=4+7+9+5+5=25. Событию А = {последний из Швеции} благоприятствуют только 9 исходов (столько, сколько участвует шведских спортсменов). Поэтому N(A)=9.
Тогда
Ответ: 0,36.
6. Элементарные события – спортсменка, выступающая первой. Поэтому N=20. Чтобы найти число элементарных событий, благоприятствующих событию А = {первой выступает спортсменка из Китая}, нужно подсчитать число спортсменок из Китая: N(A)=20-(8+7)=5. Все элементарные события равновозможны по условию задачи, поэтому
Ответ: 0,25.
7. Элементарный исход – случайно выбранная сумка. Поэтому N = 108.
Событию А = {качественная сумка} благоприятствуют 100 исходов.
Поэтому N(A) = 100.
Тогда
Ответ: 0,93.
Методическая информация
Методологическая база:
программа: Математика. 5 – 6 классы. Алгебра. 7 – 9 классы. Алгебра и начала анализа. 10 – 11 классы. Авторы – составители И.И. Зубарева, А.Г. Мордкович. Москва: Мнемозина, 2009 год.
УМК:
А.Г.Мордкович. Алгебра и начала математического анализа. 10 – 11классы. В 2 ч. Ч. 1. Учебник;
А.Г.Мордкович и др. Алгебра и начала математического анализа. 10 – 11классы. В 2 ч. Ч. 2. Задачник;
И.Р.Высоцкий, И.В.Ященко. ЕГЭ 2012. Математика. Задача В10. Теория вероятностей. Рабочая тетрадь/ Под редакцией А.Л.Семенова, И.В.Ященко. Москва. Издательство МЦНМО, 2012;
Задача В10. Открытый банк заданий по математике. ЕГЭ 2012.
интернет – источники:
http://www.toehelp.ru/theory/ter_ver/1_3/;
http://ssau2011.narod2.ru/l1.htm;
http://ru.wikipedia.org/wiki/%D2%E5%EE%F0%E8%FF_%E2%E5%F0%EE%FF%F2%ED%EE%F1%F2%E5%E9;
http://redpencil.ru/index2.php?option=com_content&task=view&id=92&pop=1&page=0&Itemid=35.








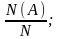 оно и будет равно вероятности события А.
оно и будет равно вероятности события А.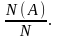
 Р(А) =
Р(А) = 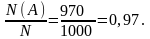
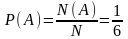 .
. .
.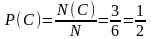 .
.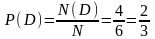 .
. 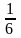 ; б)
; б) 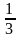 ; в)
; в) 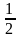 ; г)
; г) 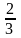 .
.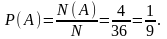
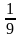 .
.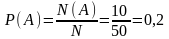 .
.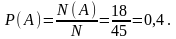
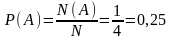 .
.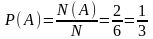 .
.