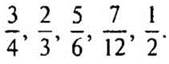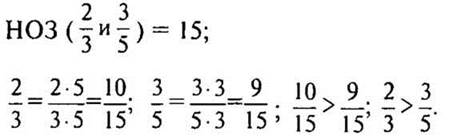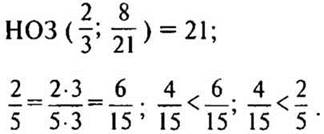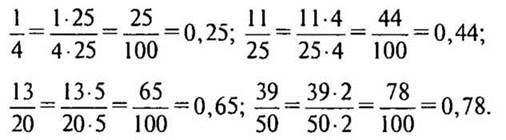Урок по теме «Сравнение дробей с разными знаменателями» ,6 класс

Урок по теме «Сравнение дробей с разными знаменателями» ,6 класс

Цели урока: поставить проблему по теме урока и найти выход из нее; вывести правила сравнения дробей с разными знаменателями; учить сравнивать дроби с разными знаменателями; продолжить формирование коммуникативных отношений.

Ход урока

I. Организационный момент

II. Устный счет

1. Назовите несколько чисел, которые имеют только три делителя. Какую закономерность можно заметить? (9, 25, 49, 81 — это квадраты натуральных чисел, сами числа являются нечетными.)

2. Сократите: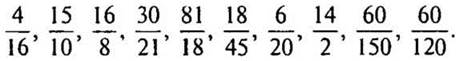 

3. Приведите дроби к наименьшему общему знаменателю: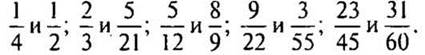 

4. Учитель проверяет все тетради за 22 мин.

Какую часть тетрадей проверит учитель за 1 мин? за 9 мин? за 16 мин?

5. Полный ящик с фруктами весит 22 кг. Ящик, заполненный наполовину, весит 12 кг. Сколько весит пустой ящик?

Решение:

1) 22 - 12 = 10 (кг) — весит половина фруктов.

2) 12 - 10 = 2 (кг).

(Ответ: 2 кг весит пустой ящик.)

IV. Индивидуальная работа

1 карточка

1. Приведите дробь 2/3 к знаменателю 9, а дробь 32/40 к знаменателю 5.

2. Приведите дроби к наименьшему общему знаменателю:

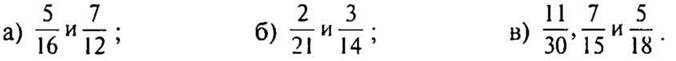
2 карточка

1. Приведите дробь 8/9 к знаменателю 18, а дробь 56/72 к знаменателю 9.

2. Приведите дроби к наименьшему общему знаменателю:

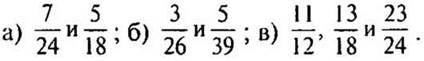
V. Сообщение темы урока

— Сегодня на уроке мы будем сравнивать дроби с разными знаменателями.

VI. Актуализация знаний учащихся

— А сейчас вспомним, как сравниваются дроби с одинаковыми знаменателями или с одинаковыми числителями.

1. Распределите числа по группам: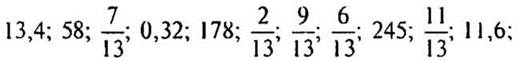 

— По какому принципу вы распределили числа?

(Ответ: на 2 группы:

целые числа: 58; 178; 245;

дробные числа: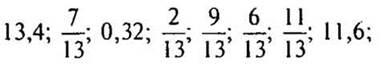 

на 3 группы:

целые числа: 58; 178; 245;

обыкновенные дроби: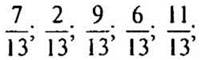 

десятичные дроби: 13,4; 0,32; 11,6.)

— Расположите данные дроби в порядке возрастания.

— А как вы узнали, что дроби надо было так расположить?

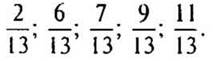
(Ответ: 2/13 — самая маленькая дробь, 11/13 — самая большая дробь).

— Какое правило сравнения дробей использовали? (Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.)

2. Запишите дроби в порядке убывания:

— Что значит записать дроби в порядке убывания? (От наибольшего числа к наименьшему числу.)

— Как сравнивать дроби с одинаковыми числителями? (Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше.)

Решение:

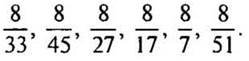
VII. Изучение нового материала

1. Подготовительная работа.

— А теперь предлагаю вам сравнить дроби. Рассмотрите их.

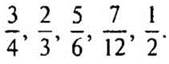
— Что вы заметили? (Знаменатели и числители у дробей разные.)

— Найдите среди этих дробей самую маленькую и самую большую.

— Появилось много мнений. У нас возникла проблема: как сравнить дроби с разными знаменателями?

— Чтобы ответить на вопрос, мы проведем исследовательскую работу. Работать будем в группах по инструкции.

(Инструкцию записать на доске.)

Инструкция:

1. Внимательно рассмотрите числа.

2. Расположите эти дроби на координатном луче, самостоятельно выберите единичный отрезок.

3. Сравните полученные отрезки. Сделайте вывод.

4. Расположите дроби в порядке возрастания. Выделите наименьшую дробь зеленным цветом, а наибольшую - красным.

5. Постарайтесь сформулировать вывод: как сравнить дроби с разными знаменателями.

— Скажите, удобно ли каждый раз, сравнивая дроби, отмечать их на координатном луче?

— Как же сравнивать такие дроби?

— Сформулируйте правило сравнения дробей с разными знаменателями и числителями.

2. Работа над новой темой.

— Сравните дроби 2/3 и 3/5.

— Приведем дроби к наименьшему общему знаменателю. (Так как 3 и 5 взаимно простые числа, то НОЗ дробей будет их произведение.)

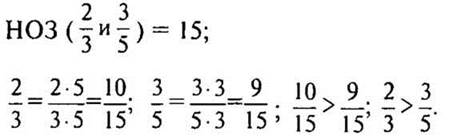
3. Учебник, стр. 50 (в некоторых учебниках опечатка — вместо слова «дательном» должно быть написано «родительном»).

— Прочитайте текст под рубрикой «Говори правильно».

— Прочитайте двумя способами данные записи: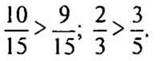 

(Десять пятнадцатых больше девяти пятнадцатых или дробь десять пятнадцатых больше дроби девять пятнадцатых.)

VIII. Физкультминутка

IX. Закрепление изученного материала

1. №№ из учебника: (у доски объясняет сильный ученик, остальные — в тетрадях).

— Как сравнивать дроби с разными знаменателями?

Решение:

а) Сравним дроби 2/3 и 8/21.

— Приведем дроби к наименьшему общему знаменателю. (Так как 21 делится на 3, то НОЗ дробей будет больший знаменатель 21.)

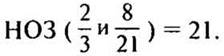
— Как сравнивать дроби с одинаковыми знаменателями? (Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.)

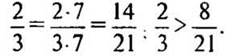
б) Сравним дроби 4/15 и 2/5.

— Приведем дроби к наименьшему общему знаменателю. (Так как 15 делится на 5, то НОЗ дробей будет больший знаменатель 15.)

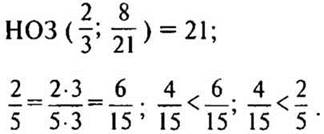
2. № 305 стр. 50 (решение записывать короче, все объяснение проговаривать).

Решение:

(Ответ: а) 1/30; б) 9/14.)

X. Самостоятельная работа

XI. Работа над задачей №№ из учебника:

— Прочитайте задачу.

— Что нужно сделать, чтобы ответить на вопрос задачи? (Сравнить дроби.)

Решение:

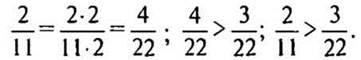
(Ответ: рисунки занимают больше места в книге.)

2. №№ из учебника: (у доски и в тетрадях).

— Что известно в задаче?

— Что надо узнать?

— Что примем за единицу? (Всю работу.)

Решение:

Пусть 1 — вся работа.

Какую часть бассейна заполняет узкая труба за 1 ч? 1/10 (часть).

Какую часть бассейна заполняет широкая труба за 1 ч? 1/4 (часть).

Какую часть бассейна заполняет узкая труба за 7 ч? 7/10 (бассейна).

Какую часть бассейна заполняет широкая труба за 3 ч? 3/4 (бассейна).

Какая труба дает меньше воды?

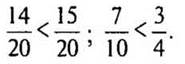
(Ответ: узкая труба.)

XII. Повторение изученного материала

№№ из учебника: (устно с подробным комментированием).

Решение:

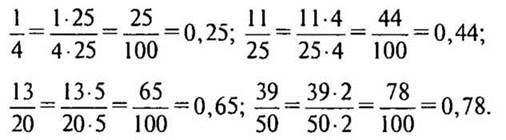
XIII. Подведение итогов урока

— Как сравнивать дроби с одинаковыми знаменателями?

— Как сравнивать дроби с одинаковыми числителями?

— Как сравнивать дроби с разными знаменателями?

Выставление оценок.

Домашнее здание.