Урок по теме "Теорема Пифагора" 8 класс

Урок ___

07.12.2020 год

8 класс

Теорема Пифагора

Тип урока: комбинированный.

Цели урока:

• обеспечить усвоение, закрепление теоремы Пифагора всеми учащимися; сформировать умение вычислять неизвестные стороны в прямоугольном треугольнике;

• через доказательство теоремы, решение задач, постановку дополнительных вопросов и заданий, развивать творческую и мыслительную деятельность учеников, их интеллектуальные качества – способность к «видению проблемы», самостоятельность, гибкость, учить объективно оценивать себя и корректировать свою деятельность в ходе урока;

• прививать интерес к геометрии, воспитывать веру в свои силы, учить коллективной и самостоятельной работе.

Структура урока:

1. Организационный момент.

2. Актуализация опорных знаний.

3. Создание проблемной ситуации.

4. Открытие новых знаний.

5. Историческая справка

6. Динамическая пауза для глаз

7. Первичное закрепление знаний

8. Домашнее задание

9. Подведение итогов урока. Рефлексия (синквейн)

1. Организационный момент

Здравствуйте, ребята! Сегодня на уроке вы получите знания по одной из немногих теорем геометрии, которую помнят все поколения. Должны знать ее и вы.

1. Актуализация опорных знаний (Слайд 2)

1. Какая фигура изображена на экране?(прямоугольный треугольник)

2. Треугольник называется прямоугольным, если у него один из углов равен… (90°)

3. Стороны прямоугольного треугольника называются (катет, катет и гипотенуза)

4. Сторона прямоугольного треугольника, лежащая против прямого угла, называется … (гипотенуза)

5. Стороны прямоугольного треугольника, образующие прямой угол, называются ... (катетами)

6. Сумма острых углов прямоугольного треугольника равна …(90°)

7. Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине …(гипотенузы)

8. Площадь квадрата равна квадрату его…(стороны)

9. Площадь прямоугольного треугольника равна…( a*b )

1. Создание проблемной ситуации

Задача: (Слайд 3)

На берегу реки рос тополь одинокий.

Вдруг ветра порыв его ствол надломал.

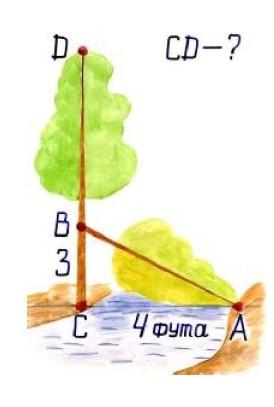Бедный тополь упал. И угол прямой

С теченьем реки его ствол составлял.

Запомни теперь, что в этом месте река

В четыре лишь фута была широка

Верхушка склонилась у края реки.

Осталось три фута всего от ствола,

Прошу тебя, скоро теперь мне скажи:

У тополя как велика высота?»

- Предложите алгоритм решения задачи. (Ответы учеников)

- При решении задачи возникла проблема: недостаточность знаний.

- Помочь выйти из данной ситуации, расширить свои знания нам поможет одна из немногих теорем геометрии, которую помнят все поколения. Должны знать ее и вы - теорема Пифагора, которая позволяет находить неизвестную сторону прямоугольного треугольника по двум известным сторонам.

4. Открытие новых знаний

Запишите сегодняшнее число и тему нашего урока

(слайд 4)

Практическое задание на доказательство теоремы: (слайд 5)

Начертите в тетрадях прямоугольный треугольник с катетами а и в:

1ряд - 3 и 4; 2ряд - 6 и 8;

измерьте его гипотенузу и заполните таблицу

сравните сумму квадратов катетов с квадратом гипотенузы.

Сделайте вывод: в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. Это утверждение и есть теорема Пифагора (гипотеза).

(Слайд 6) Теорема:
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

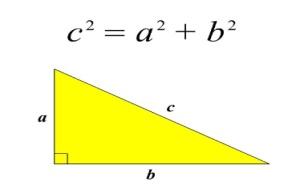
- Ребята! Утверждение, которое вы только что сформулировали, является одной из важнейших теорем геометрии и имеет своё имя – теорема Пифагора

И так подведем итог нашей работы: (стихотворение)

Если дан нам треугольник,
и притом с прямым углом,
то квадрат гипотенузы
мы всегда легко найдем:
катеты в квадрат возводим,
сумму степеней находим -
и таким простым путём
к результату мы придём. (Слайд 7)

Видео-материал «Теорема Пифагора» (слайд 8),

«Доказательство теоремы Пифагора» (слайд 9)

1. Историческая справка

ПИФАГОР САМОССКИЙ (ок. 580 – ок. 500 г. до н.э.) (слайд 10)

О жизни Пифагора известно немного. Он родился в 580 г. до н.э. в Древней Греции на острове Самос, который находится в Эгейском море у берегов Малой Азии, поэтому его называют Пифагором Самосским.

В молодости Пифагор был учеником Фалеса, которому в то время шёл восьмой десяток, побывал в Египте, где учился у жрецов. Говорят, что он был допущен в сокровенные святилища Египта, посетил халдейских мудрецов и персидских магов.

(Слайд 11). В 530 г. до н.э. Пифагор основал так называемый пифагорейский союз. Около сорока лет учёный посвятил созданной им школе.

Пифагорейцы, как их позднее стали называть, занимались математикой, философией, естественными науками.

Пифагорейцами было сделано много важных открытий в арифметике и геометрии, в том числе:

1) теорема о сумме внутренних углов треугольника;

2) построение правильных многоугольников и деление плоскости на некоторые из них;

3) геометрические способы решения квадратных уравнений;

4) деление чисел на чётные и нечётные, простые и составные; введение фигурных, совершенных и дружественных чисел;

5) доказательство того, что   не является рациональным числом;

6) создание математической теории музыки и учения об арифметических, геометрических и гармонических пропорциях и многое другое.

Известно также, что кроме духовного и нравственного развития учеников Пифагора заботило их физическое развитие. Он не только сам участвовал в Олимпийских играх и два раза побеждал в кулачных боях, но и воспитал плеяду великих олимпийцев.

(Слайд 12). Доказательство теоремы Пифагора считалось в кругах учащихся средних веков очень трудным и называлось иногда Pons Asinorum “ослиный мост” или elefuga – “бегство убогих”, так как некоторые “убогие” ученики, не имевшие серьезной математической подготовки, бежали от геометрии.

Слабые ученики, заучивавшие теоремы наизусть, без понимания, и прозванные поэтому “ослами”, были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста.

Пифагор сделал много важных открытий, но наибольшую славу учёному принесла доказанная им теорема, которая сейчас носит его имя.

1. Динамическая пауза для глаз (слайд 13)

2. Закрепление знаний

Вернемся к задаче (слайд 3)

(Слайд 15)Зачем нам нужна теорема Пифагора? ( Для того чтобы находить стороны прямоугольного треугольника.)

С помощью теоремы Пифагора можно решать два вида задач:

1.Найти гипотенузу прямоугольного треугольника, если известны катеты.

2. Найти катет, если известна гипотенуза и другой катет

Решение задач из учебника: № 483(а, б), 484(а, б); (на фоне звучит музыка числа ПИ)

Приложение 1

(слайд 16)

1. Домашнее задание (слайд 17)

Выучить ответы на вопросы № 8-10, решить задачи №491, 492, 494(всем)

Для тех, кто желает больше узнать о Пифагоре, прочитать о нём легенды, выяснить, почему союз пифагорейцев был тайным, почему авторство работ приписывалось учителю.

А тем, кто желает не только больше узнать, но и рассказать другим, я предлагаю приготовить рефераты или проекты по данному материалу.

1. Подведение итогов. Рефлексия (Слайд 18)

Синквейн - стихотворение, состоящее из пяти строк.

1- имя существительное (теорема Пифагора)
2- 2 прилагательных (строгая, логичная)
3- 3 глагола, отражающие ваши действия (строим, доказываем, вычисляем)
4- крылатая фраза (квадрат гипотенузы равен сумме квадратов катетов)
5- вывод (прямоугольный треугольник)

Благодарю вас всех за активную работу на уроке. (слайд 19)