10
План-конспект открытого урока по теме: «Замечательные кривые».
Ершова Ирина Васильевна учитель математики
Предмет: алгебра.
Класс: 10.
Тема: Замечательные кривые
Тип урока: изложение нового материала.
Цели урока:
Образовательная: сформировать целостное представление о «замечательных» кривых, добиться осмысления трех составляющих понятия «замечательные» кривые, продемонстрировать способы их приложения, подчеркнуть межпредметные связи в раскрытии данной темы
Воспитательная: воспитывать трудовые навыки, чувство ответственности, эстетическое начало, стимулировать любознательность и творческую деятельность;
Развивающая: развивать общекультурный уровень, учебные навыки устной речи, самостоятельной работы, коммуникативные навыки, анализа и синтеза, пространственной ориентировки, зрительного представления, творческого воображения.
Оборудование и пособия: интерактивная доска, анимационные слайды, осветитель, вращающаяся доска, рабочие листы с печатными заготовками, большой надувной мяч для физкультминутки.
Этапы урока
| № | этап |
| 1 | Целеполагание |
| 2 | Знакомство с замечательными кривыми в геометрическом представлении |
| 3 | Замечательные кривые в алгебраическом представлении. |
| 4 | Тренировочное закрепление |
| 5 | Физкультминутка «движение по параболе». |
| 6 | Замечательные кривые как орбиты движений |
| 7 | Подведение итогов. |
Ход урока
1 . Целеполагание.
Приветствие.
Я бросаю на пол какой-нибудь предмет. Охарактеризуйте, пожалуйста, это падение, как он упал?
-Вниз. – Согласна.
-Быстро. –Согласна.
-Прямо. – Не согласна.
Этот предмет упал не прямо. Дело в том, что прямолинейного движения в не существует вообще в природе!
И, если вы об этом не подозревали, то как раз сегодня вам предстоит пересмотреть свою точку зрения.
А если никакие предметы в мире не двигаются прямо, то как же они двигаются? Ответ на этот вопрос кроется в теме нашего сегодняшнего урока.
Бывает много замечательных затей,
Бывает жизнь замечательных людей,
Есть много фильмов замечательных и книг,
А наш вопрос – о замечательных кривых.
Ответьте, прослушав внимательно:
Так чем же они замечательны?
2. Знакомство с замечательными кривыми в геометрическом представлении
И чтобы пролить свет на этот вопрос, я воспользуюсь осветителем. В классе выключается свет. Луч прожектора направлен перпендикулярно плоскости вращающейся доски.

Мы видим, что прожектор осветителя представляет из себя расходящийся из точечного источника пучок света. Какую геометрическую форму он имеет? /конус/.
Он направлен на поверхность доски, которая пересекает его. Такая плоскость называется по отношению к нему…? /секущей/
Что за фигура получается в сечении? /окружность/.
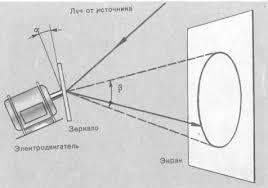
А теперь представьте, что получится, если я наклоню секущую плоскость доски, что произойдет с окружностью, во что она превратится? /она вытянется/. Давайте, проверим. Как называется такая фигура? /эллипс/

Если же я еще больше увеличу угол наклона плоскости так, чтобы линия контура вышла за край доски, кто-нибудь скажет ее название? Смотрим, что получается. /парабола/.

А теперь я сделаю этот угол наклона доски по отношению к направлению луча прожектора тупым. Кто-нибудь знает, что это за линия? /гипербола/.
В классе включаем свет.
Подытожим: какие линии мы можем получить путем сечений конуса? /окружность, эллипс, гипербола, парабола). Совместим полученные данные нашего опыта на одном чертеже.

Итак, мы видим, как получили 4 линии, которые вы легко узнали, потому что уже встречались с ними, но только две из них мы встречали в курсе алгебры, а две – курсе геометрии. Какие из них где? (Окружность и эллипс – геометрия, парабола и гипербола – алгебра).
И вот сегодня они так неожиданно вместе встретились и оказались связаны общим происхождением – путем сечений конуса, и потому все они носят названия конических сечений.
Обратимся к теме урока. Вот и первая их замечательная особенность.
Кстати, отсюда же - происхождение их названий. Откуда окружность берет свое название, понятно – от слова «окружать». А вот что касается остальных кривых, то объяснение их названий не очевидно, и оно кроется в результате сечений конуса.
Я сейчас буду называть смысловое значение их названий, а вы попытайтесь догадаться, как произведенные сечения могут эти названия объяснить.
Итак, слово «парабола» означает «равенство».
Может быть, кто-то из вас сам объяснит значение слова «гипербола», обращаясь к урокам литературы, где вы проходили такое понятие, как «литературная гипербола», или, к примеру, вспомните такие слова, как «гиперактивность», «гиперкомпенсация», «гипермаркет»? /Избыток/.
А теперь догадаетесь, что может значить слово «эллипс» ? /Недостаток/.
А сейчас посовещайтесь и предложите свои версии происхождения этих названий.
/Ответ. «Парабола» означает «равенство», т. к. плоскость параболы проходит параллельно образующей, и угол наклона плоскости для получения гиперболы увеличивается, поэтому слово означает избыток, угол наклона секущей плоскости для получения эллипса уменьшается, поэтому это слово означает «недостаток»./

3. Замечательные кривые в алгебраическом представлении .
Эти кривые замечательны еще и тем, что не только своим происхождением обязаны коническим сечениям, они так же имеют и совершенно иное непохожее происхождение.
Рассмотрим в качестве примера уравнение  .
.
Какого оно порядка? Второго.
Но этого пока не достаточно, чтобы понять, какую линию оно задаёт.
Немного потраченного времени, и вы сможете научиться довольно легко находить ответы на эти вопросы, в частности, без особых проблем сможете определить, что данное уравнение определяет эллипс, который расположен центром в точке  и повёрнут относительного своего канонического положения на отрицательный угол, составляющий примерно
и повёрнут относительного своего канонического положения на отрицательный угол, составляющий примерно  :
:
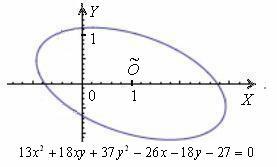
А сейчас мысленно возьмите эллипс в руки, поверните его на любой угол и переместите в произвольное место плоскости. Новому положению эллипса будет соответствовать совершенно другое уравнение, и если вам предъявить его без чертежа, то никто в жизни не догадается, что оно определяет тот же самый эллипс. Именно поэтому и появилась задача приведения уравнения к каноническому виду – чтобы независимо от расположения линии выяснить, какую форму она принимает.
Рассмотрим эту задачу, и вы увидите, какое отношение все сказанное имеет к нашей теме и что нового это поможет нам открыть в области познания замечательных кривых.
Для выполнения этого задания разделитесь на три группы, каждая из которых получит свое уравнение, которое предстоит привести к каноническому виду. Подсказка: воспользуйтесь приемом выделения полных квадратов. А какой вид кривой будет описывать полученное вами уравнение, я вам подскажу.
Разбор решений каждой группы.
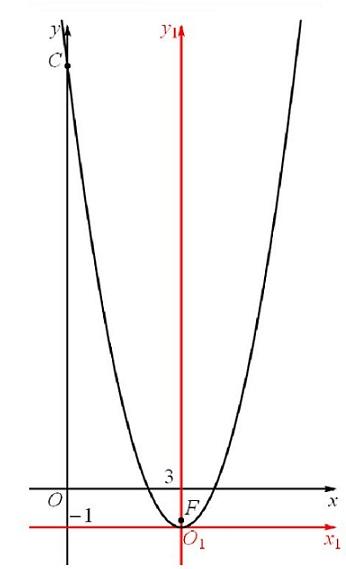
1 группа.

И это есть уравнение параболы с центром о точке О (3;-1)
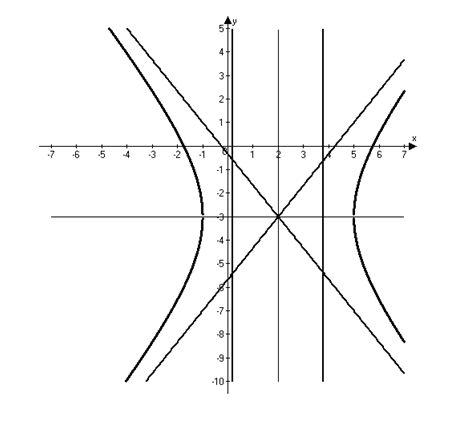
2 группа.

В вашем случае уравнение это уравнение гиперболы с центром в точке С(2;-3), оси гиперболы будут лежать на прямых х=2, у=-3.
3 группа.

А здесь мы получили уравнение эллипса с центром в точке С(-2;3).
И вот снова мы получаем знакомые замечательные кривые, теперь уже на графике!
А вот совмещенная картинка, которая дает нам представление об этой еще одной замечательной связи кривых: все они получаются из одного канонического уравнения. Вот его общий вид:

Придавая его коэффициентам определенные значения, мы получаем все те же замечательные кривые.

А поскольку все они объединены происхождением из уравнения второго порядка, то и названы они также кривыми второго порядка.
5. Физкультминутка «движение по параболе»
Но и это еще не все то замечательное, чем связаны эти кривые. Оказывается, все они являются линиями движения тел. И в этом мы сейчас убедимся. Для этого нам понадобится вот этот большой надувной мяч. Оставайтесь все на своих местах и перебрасывайте его друг другу.
А теперь скажите, как называется траектория, по которой двигался мяч?- Как известно из курса физики, тело, брошенное под углом к горизонту движется по параболе.
4. Замечательные кривые как орбиты движения тел.
Верно, это парабола.

И даже более того: тело, брошенное вниз, как в примере в самом начале нашего урока, так же движется не прямо. И когда мы спрашиваем у прохожего дорогу, а он отвечает: «Идите прямо», - это допущение, потому что вообще-то, движения по прямой не существует в мире! Почему? А вот каким увидел бы это движение виртуальный наблюдатель, находящийся где-нибудь на луне. (Картинка изображена для наглядности с несоблюдением масштаба).

Почему это так? (Потому что тело испытывает притяжение вращающейся Земли).
А теперь я вам я предложу такой вопрос: если задать телу такую большую скорость, чтобы оно достигло верхних слоев атмосферы, по какой траектории оно будет тогда двигаться? И какой может быть пример такого объекта? /Действие силы притяжения будет удерживать тело на этой высоте, и оно будет облетать Землю. Эта траектория – окружность. Пример: спутник Земли

А если задать телу такую большую скорость, чтобы оно пересекло верхние слои атмосферы, по какой траектории оно будет тогда двигаться? И снова подумайте, что бы это мог быть за объект, который так движется? /Гипербола, не прямая, т. к. тело стартует с движущейся Земли. Это как прыжок с движущегося вагона, направление движения искривляется. И таким телом может являться ракета/.

А вот как еще могут двигаться тела. Узнаете эту картинку? Что она изображает?
(Движение планет вокруг солнца). По какой траектории движутся планеты вокруг Солнца? - По эллипсам.
А вообще, Исаак Ньютон вывел закон о том, что, если телу задать начальную скорость и направление, то орбита его движения примет только одну из четырех форм: окружность, гипербола, парабола, эллипс.
Мы снова увидели, как наши замечательные кривые замечательны еще и тем, что описывают такой важный физический закон.
5. Подведение итогов
Вернемся к вопросу, поставленному в начале урока.
Бывает много замечательных затей,
Бывает жизнь замечательных людей,
Есть много фильмов замечательных и книг,
А наш вопрос – о замечательных кривых.
Ответьте, прослушав внимательно:
Так чем же они замечательны?
Ученики обобщают полученные представления о кривых как о конических сечениях, кривых второго порядка и орбитах движения тел.

































