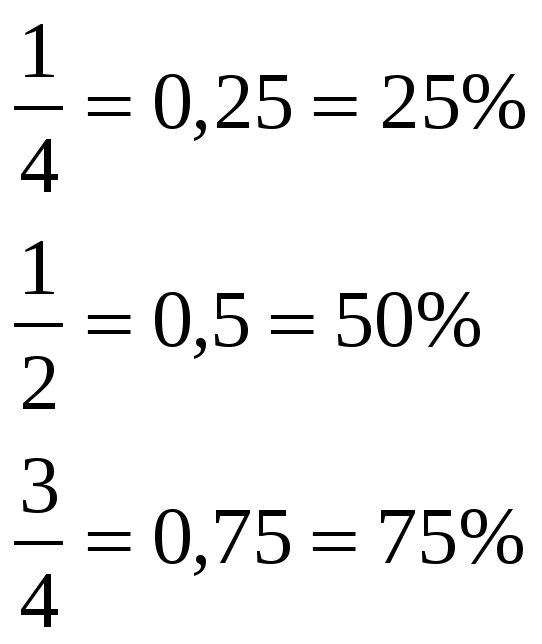Урок по теме "Проценты "

Деятельность учителя

Деятельность ученика

1. Организационный момент:

Здравствуйте, присаживайтесь. Начнем урок с проверки домашнего задания.

• У кого возникли затруднения при выполнении домашней работы, поднимите руку?

• Прочитайте задачу, записанную на экране (слайд 1).

• Можем мы ее сейчас решить?

• А почему, нам что-то не знакомо?

• Тогда как мы сформулируем тему нашего урока? (слайд 2)

• Какие сегодня задачи стоят пред нами?

• Попытаться решить данную задачу в конце урока.

Задают вопросы по заданиям, которые вызвали затруднения.

Читают задачу

Нет.

Мы не знаем, что такое проценты с точки зрения математики и как с ними работать.

Проценты. Записывают в тетрадях дату, тему урока.

Выяснить, что понимают под процентами.

Научиться решать задачи содержащие проценты.

2. Актуализация знаний:

• Поднимите руку, кто знаком со словом «проценты».

• Опишите ситуации, где приходилось встречаться с этим словом.

Мы очень часто встречаемся с этим понятие в повседневной жизни (слайд 3).

Таким образом, мы приходим к выводу, что изучение темы «Процент» необходимо не только в рамках предмета математики, но и для удовлетворения бытовых потребностей любого человека.

Прежде чем приступить к изучению новой темы, решим устно задачи.

1. У меня было 500 рублей. На тетрадь я потратил своих денег. Сколько рублей стоила тетрадь?

1. На конфеты я потратил 25 рублей, что составило имевшихся у меня денег. Сколько денег было?

В магазине, в банке и т.д.

Ответ: 5 рублей стоила тетрадь.

Ответ: было 2500 рублей.

3. Изучения нового материала:

В первой задаче, мы с вами находили сотую часть, а во второй нам была известна сотая часть, мы находили целое.

Еще в древности люди заметили, что сотые доли величин удобны в практической деятельности. Поэтому для них было придумано специальное название – процент.

В математике сотую часть любой величины: пути, массы, объема и т.п - процент.

Придумана даже специальная запись (символ, обозначение) слова «процент» - %.

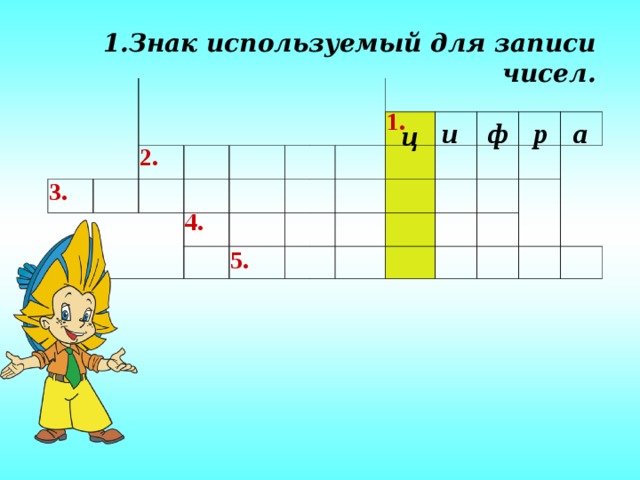
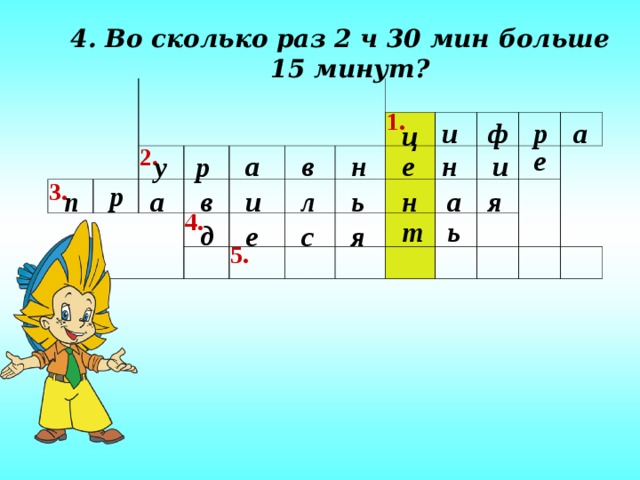
Чтобы узнать, откуда к нам пришло слово процент разгадаем кроссворд (приложение 1).

Слово «процент» происходит от латинского слова «центи», указывающего на уменьшение единицы измерения в 100 раз (слайд 6-11).

Сейчас мы выполним небольшое задание (слайд 12-15).

Задание №1. Даны квадраты , необходимо закрасить 20 %, 50%; 100%.

Задание №2. Необходимо указать:

1. сколько процентов площади квадрата составляет площадь закрашенной фигуры.

2. какую часть площади квадрата составляет площадь закрашенной фигуры?

   • А как рациональным способом можно найти, сколько процентов поля не закрашено?

Каждому ученику выдается лист с изображением частично закрашенных квадратов (Приложение 2).

• Какой мы можем сделать вывод из выше сказанного?

Физкультминутка (слайд 16):

Следует особо обратить внимание на то, что дробь и процент выражают одно и то же отношение между целым и частью, поэтому мы должны уметь переходить от дроби к процентам и наоборот.

• Как сформулировать правила перевода десятичной дроби в проценты?

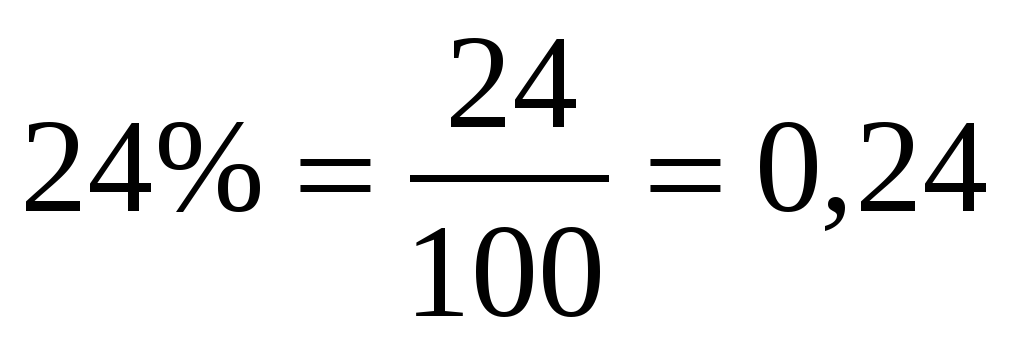
Прочитайте правило в учебнике на странице 237.

Работа с учебником № 1562.

• Тогда как представить обыкновенную дробь в процентах.

• Проговорите еще раз правило.

• Что нужно сначала сделать?

• Как обыкновенную дробь представить в виде десятичной?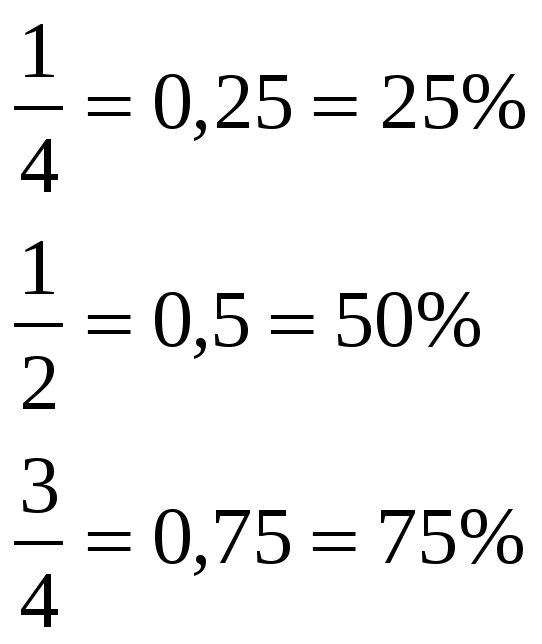

• Тогда как сформулировать правило обратного перевода из процентов, в десятичную дробь.

Прочитайте правило в учебнике на странице 237.

Работа с учебником №1561.

Записывают в тетради

Фронтально отвечают на вопросы кроссворда.

Один из учащихся вслух зачитывает историческую справку.

Решение осуществляется учащимися «по цепочке» с комментариями.

Выполняют задания, записывая ответы на листах.

Все поле 100%, закрашено 30 %, следовательно, не закрашено 70%.

С помощью процентов можно выразить отношение между двумя величинами: частью и целым. Удобно то, что мы имеем дело не с дробями, а с целыми числами, хотя речь идёт о той же величине.

Вся величина 100 %.

Чтобы обратить десятичную дробь в проценты надо умножить ее на 100 .

Читают правило в учебнике.

1 пример разбираем на доске, остальные самостоятельно с последующей проверкой.

Проговаривают правило.

Представить ее в виде десятичной дроби.

Разделить числитель на знаменатель.

Чтобы перевести проценты в десятичную дробь, надо разделить число процентов на 100.

1 пример разбираем на доске, остальные самостоятельно с последующей проверкой.

1. Первичное закрепление пройденного материала

Выдается листы с заданиями (слайд 16-21).

Оценивание:

Выполняют задания, записывая ответы на листах.

Поднимают карточки с указанными смайликами.

1. Подведение итогов

Вернемся к первой задаче, которую мы не смогли решить в начале урока (слайд 22).

• Что мы сперва сделаем?

• Что такое процент?

• Как перевести процент в десятичную дробь и наоборот?

Переведем проценты в обыкновенную дробь. Получим, что 65 % =

Ответ: 6500 человек приняли участие в выборах.

Формулируют определение процента, правила перевода десятичной дроби в проценты и наоборот.

1. Домашнее задание

п 40, №1598; №1599, № 1594 (слайд 23)

Записывают в дневники домашнее задание

ц

и

ф

р

а

у

р

а

в

н

е

н

и

е

п

р

а

в

и

л

ь

н

а

я

д

е

с

я

т

ь

п

е

р

и

м

е

т

р

Даны квадраты , необходимо закрасить 20 %, 50%; 100%

1)Сколько процентов площади квадрата составляет площадь закрашенной фигуры?

2) Какую часть площади квадрата составляет площадь закрашенной фигуры?

1)

2)

______________________________________________________________Ф.И

1. Процент- это:…

а) тысячная часть числа;

б) сотая часть числа;

в) десятая часть числа.

2. 8% - это:..

а) 0,08;

в) 0,008;

г) 0,0008.

3. 0,269 –это:..

а) 269%;

б) 2,69%;

в) 26,9%

4. 25% класса –это:

а) половина учеников;

б) четверть учеников класса;

в) пятая часть класса.

5. Картофелем засажено 51% поля. Сколько процентов поля осталось засадить картофелем?

а) 151 %

б) 49 %

в)