Урок. Решение задач с помощью пропорций в 6 классе

Описание методической идеи.

Данная разработка является примером дифференцированного подхода в обучении математики. Тема «Решение задач с помощью пропорций» является разработкой системы уроков, на которых учащиеся сначала знакомятся со способом решения задач с помощью пропорций, имея возможность сравнить его с уже известным способом, убедиться в универсальности, «удобности», простоте изучаемого способа решения задач. То есть данный проект построен по принципу «от простейшего - к сложному». Работа учащихся на уроках представлена в различной форме: это и коллективное обсуждение условия задачи, это и работа по индивидуальным карточкам различного уровня сложности, это и творческие задания.

Условно всю разработку можно разделить на 3 этапа, каждый из которых, в свою очередь, подразделяется на уровни сложности:

1.Подготовительный этап.

2.Этап ознакомления с решением задач с помощью пропорций.

3.Этап закрепления умения решать задачи с помощью пропорций.

Отличительной особенностью данной разработки является:

1. включение задач различного типа, но решаемых с помощью пропорции

( задачи «на движение», «на работу», бытового характера),

1. включение различных видов работы с задачей, решаемой с помощью пропорции: работа с задачей, записанной в виде краткой записи, в виде таблицы, рисунка, схемы,

2. деятельность учащихся на уроке имеет поисково-исследовательский, творческий характер,

3. украшением и ярким воспитательным моментом темы являются задачи о исчезающих видах животных, птиц, рыб. Это заключительный, запоминающийся этап изучения темы,

4. использование презентаций к урокам являются необходимым дополнением учебного процесса, помогающим более рационально использовать время на уроке, сделать некоторые моменты в решениях задач более понятными, яркими, запоминающимися,

5. универсальность применения, так как данную разработку любой учитель может «сжать» до необходимого количества часов, опираясь на базовые типы задач; остальные же задачи можно дать учащимся в качестве дополнительных заданий или вынести для решения на математический кружок, факультатив. Т.е. учитель по своему усмотрению может «набрать» нужные ему уроки по изучаемой теме из данной разработки, а при желании использовать все этапы разработки на одном уроке,

6. индивидуальный подход в обучении, разноуровневость задач, позволяющая каждому ученику решить «свою» задачу и уйти с урока с чувством освоенной математической вершины .

Необходимые ресурсы для запуска проекта:

1. программа Microsoft Office Word 2003,

2. программа Microsoft Office PowerPoint 2003,

3. экран и мультимедийная установка любого типа или интерактивная доска.

Источник информации:

1. «Математика» (в помощь выпускнику школы и абитуриенту) Н.Л.Васильева, изд. «Паритет», 2000.

2. «Дидактические материалы по математике, 6», А.С.Чесноков, К.И.Нешков, изд. «Просвещение», 2000.

3. «Тесты по математике 5-11 классы» М.А.Максимовская, изд. «Олимп», 2003.

4. Адреса интернет - сайтов: http://mad-love.ru/zoo.php?grp=1 &item=808

План-конспект уроков:

Предмет: математика.

Класс: 6.

Тема урока: Решение задач с помощью пропорций.

Используемый УМК:

Программы для общеобразовательных школ, гимназий, лицеев. Математика. 5-11 классы. Программы. Тематическое планирование. – М.: Дрофа, 2004.

Учебник «Математика,6» Виленкин Н.Я. , изд. «Мнемозина», 2006.

Дидактические материалы по математике, 6, А.С.Чесноков, К.И.Нешков, изд. «Просвещение», 2000.

Цель: 1.обучающая: научить учащихся правильно определять тип пропорциональной зависимости, описанный в задаче, правильно составлять краткую запись к задаче, пропорцию, правильно уметь оценить полученный ответ,

2.развивающая : развить навыки решения пропорций, задач с помощью пропорций, определения типа пропорциональной зависимости, развить творческие способности и их логическое мышление, навыки поисково-исследовательской работы на уроке,

3.воспитывающая: воспитать навыки работы в коллективе, самостоятельной работы, воспитать бережное отношение к природе.

Ход урока:

Приветствие .

1.Подготовительный этап.

Для того, чтобы можно было приступить к решению задач с помощью пропорций, сначала необходимо :

1. проверить умение учащихся находить неизвестный член пропорции. Это можно сделать во время устного счета с помощью готовых карточек с пропорциями или с применением презентации (приложение 1- слайд 1)

Х:3=4:6 5:Х=2:6

7:3=Х:18

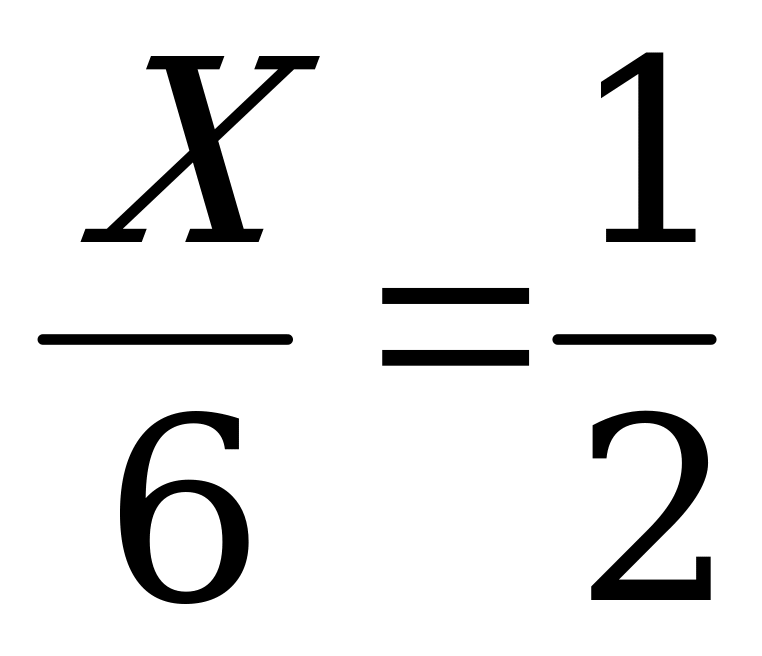
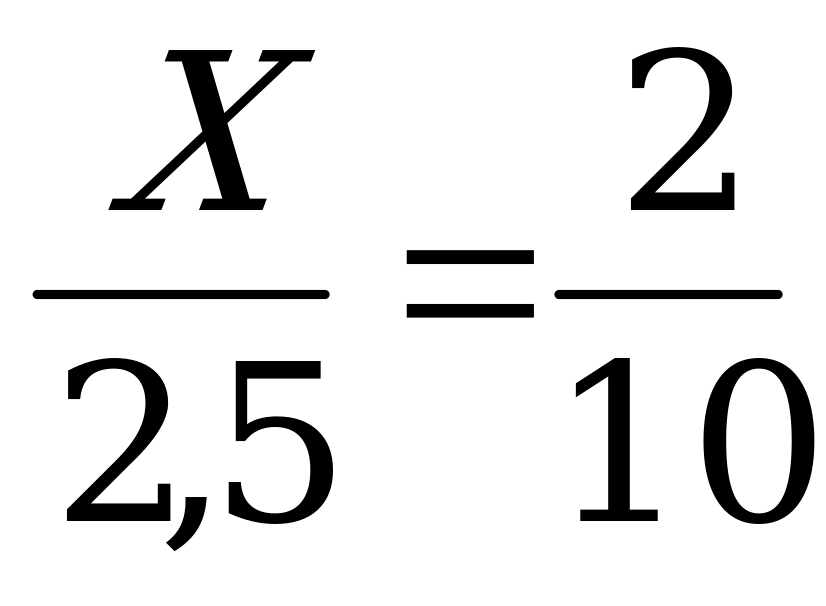
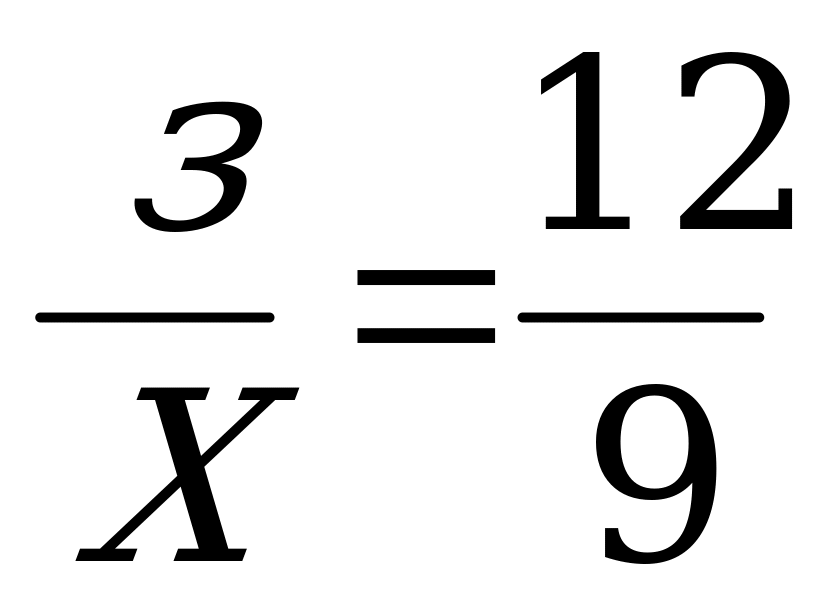
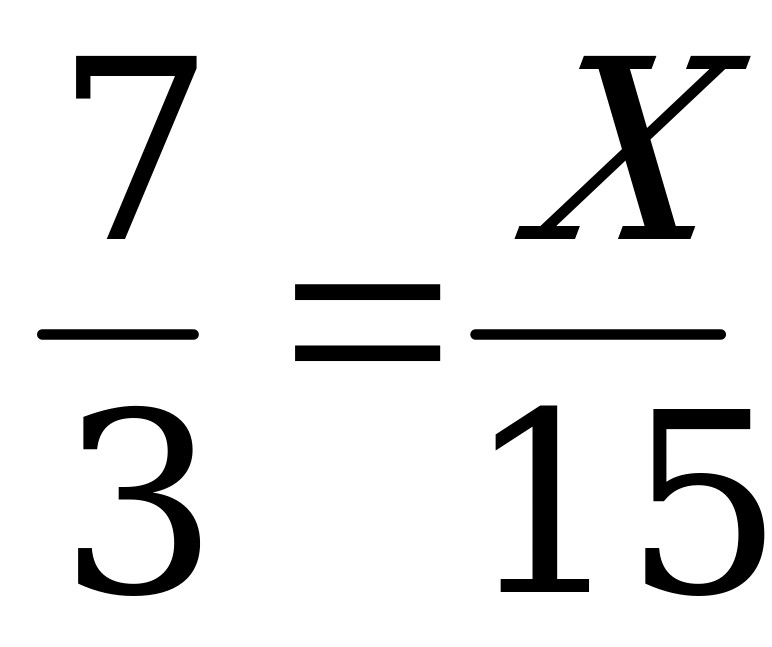
затем можно решить в тетрадях несколько пропорций:

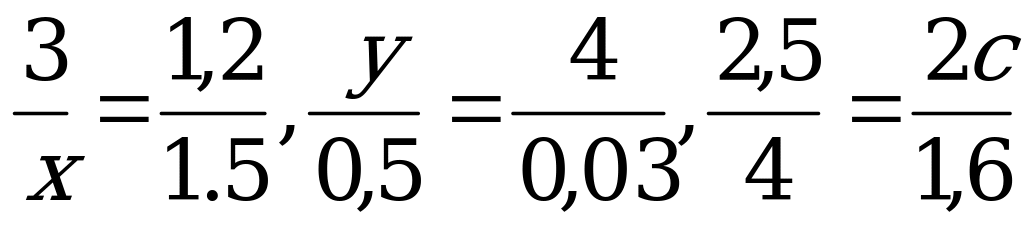
1. проверить умение учащихся узнавать прямо и обратно пропорциональную зависимость.

Для этого учащиеся

а) приводят устно примеры пропорциональных зависимостей (зависимость длины материи и ее стоимости, объема воды и ее массы и т.д.);

б) проверяют правильность составления прямо пропорциональной и обратно пропорциональной зависимостей по карточкам, заготовленным учащимися дома. Для этого берется карточка любого ученика, и все учащиеся определяют вид зависимости величин в ней, проверяют правильность ее составления;

в) работают устно по карточкам (слайдам), представленных учителем (приложение 1-слайд 2):

для этого учащиеся заполняют пустые клеточки и определяют вид пропорциональной зависимости:

Съеденное варенье из банки (г)	100	200	300	400
Оставшееся варенье в банке (г)				300

s	v	t
?	50 км/ч	2 ч
?	50 км/ч	3 ч

s	v	t
100 км	?	2 ч
200 км	?	2 ч

Какова зависимость пути от времени? Какова зависимость пути от скорости?

Г) глядя на рисунок, ученики должны придумать величины пропорциональной зависимости и определить ее вид (приложение 1- слайд 3) :

Д) отгадывают загадку и указывают вид пропорциональной зависимости в ней:

Чем больше из нее берешь,

тем больше она становится.

(Яма)

2.Этап ознакомления со способами решения задач с помощью пропорций.

Ознакомление можно начать с таких простейших задач основных видов: (приложение 1-слайды 4,5,6):

1.В 2,5 кг сиропа содержится 1,2 кг сахара. Сколько сахара содержится в 3 кг такого же сиропа?

2.Из 30 кг свежих яблок выходит 10,5 кг сушеных. Сколько надо взять свежих яблок, чтобы получить 14,7 кг сушеных?

3.Со 125 гусей получают 4 кг пуха. Сколько пуха можно получить с 875 гусей?

Задача на нахождение процентного отношения:

4.В 85 г железной руды содержится 51 г железа. Сколько процентов железа содержится в железной руде?

Задача на нахождение числа по его проценту:

5.Яблоки при сушке теряют 84% своей массы. Сколько надо взять свежих яблок, чтобы получить 64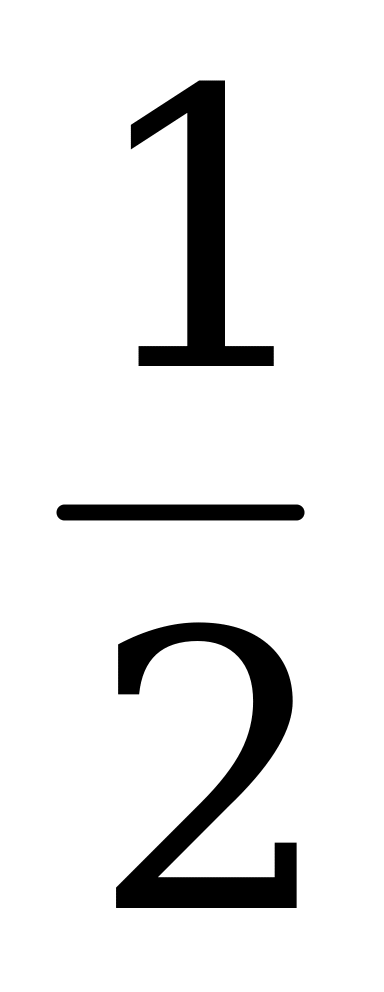 кг сушеных?

6.Из 35 учеников класса 60% учатся на «4» и «5». Сколько учеников класса учатся на «4» и «5»?

7.Завод за месяц выпустил 3360 машин, что составило 140% его месячного задания. Найти месячный план завода.

Задача нахождения процентов от числа:

8.Еще недавно с каждого гектара собирали 35 центнеров пшеницы. Теперь собирают 42 центнера с каждого гектара. На сколько процентов повысилась урожайность пшеницы?

Задача на нахождение числа по его дроби:

9.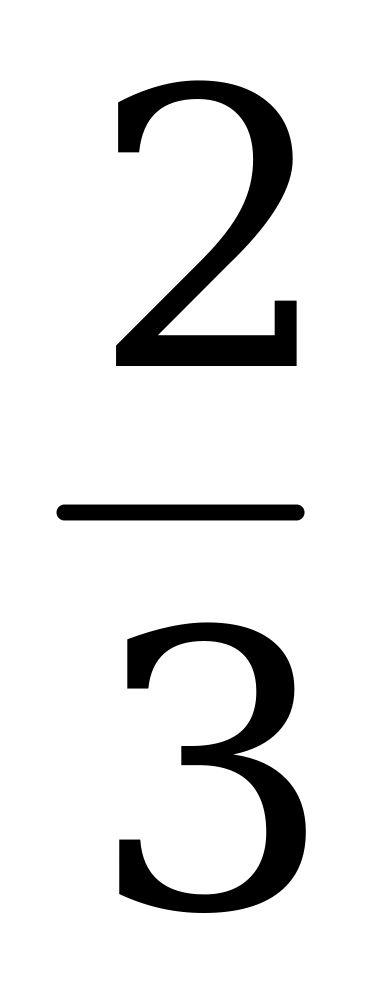 килограмма товара стоят 30 рублей. Сколько стоит 1 кг товара? 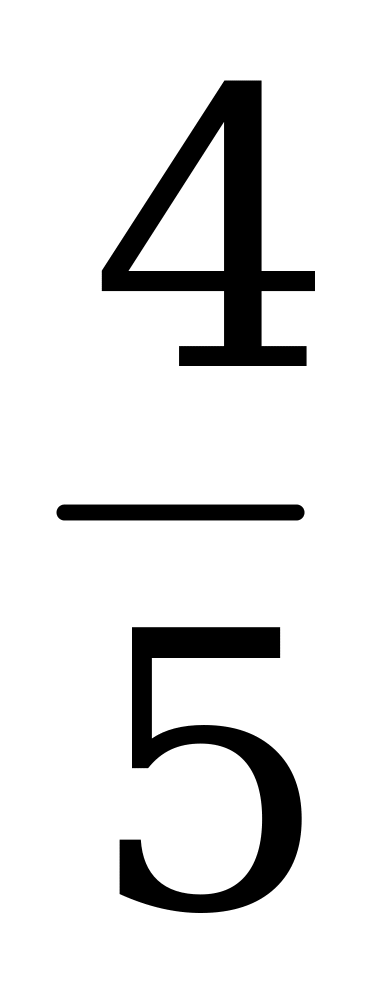кг товара?

Можно начать с задач 1-4 по такому плану:

1)ознакомление с содержанием задачи:

А) чтение задачи,

Б) проверка понимания содержания задачи с помощью вопросов,

В) составление краткой записи в виде

Сироп Сахар Свежие яблоки Сушеные яблоки

2,5 кг - 1,2 кг 30 кг - 10,5 кг

3 кг - х кг х кг - 14,7 кг

1. поиск решения задачи новым способом:

а)построение рассуждений:

после составления краткой записи учащимся предлагается ответить на такие вопросы:

1.Если увеличивать массу сиропа, то как будет изменяться масса содержащегося в нем сахара?

2.Если масса сиропа увеличится в 3 раза, то во сколько раз увеличится масса сахара в нем?

3.Какой это вид пропорциональной зависимости ?

4.Как можно в краткой записи показать вид пропорциональной зависимости?

5.Как узнать, во сколько раз увеличилась масса сахара, масса сиропа? (с помощью отношения)

6.Можем ли мы приравнять эти два отношения? Почему?

7.Что получилось после того, как мы приравняли два отношения?

Таким образом, краткая запись и начало решения задачи должны выглядеть так:

С ироп Сахар

2,5 кг - 1,2 кг

3 кг - х кг

Составлю и решу пропорцию:

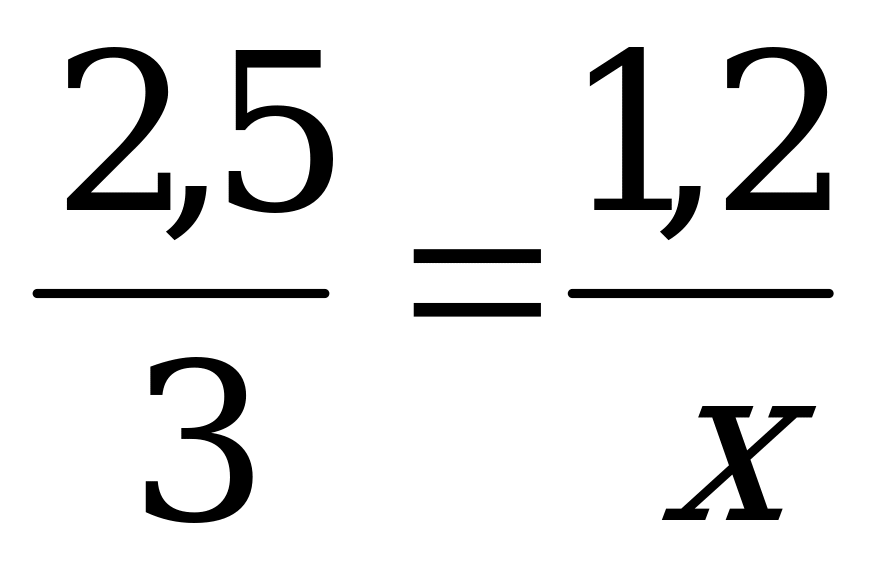
б) далее учитель предлагает учащимся составить план решения задач с помощью пропорций:

План решения задач с помощью пропорций:

1.Составление краткой записи к условию задачи.

2.Определение вида пропорциональной зависимости.

3.Составление пропорции.

4.Нахождение неизвестного члена пропорции.

5.Проверка ответа по смыслу.

3)решение задач разного типа:

К предложенным задачам нужно добавить задачи на обратно пропорциональную зависимость (приложение 1-слайд 7):

10. 4 комбайнера могут убрать пшеницу с поля за 10 дней. За сколько дней уберут это поле 5 таких же комбайнеров?

11. Поезд, скорость которого 45 км/ч, затратил на некоторый участок пути 4 часа.За сколько часов пройдет этот путь поезд, если его скорость станет 40 км/ч?

12. Из некоторого количества пряжи выходит 90 м ткани шириной 60 см.Сколько метров ткани выйдет из этого же количества пряжи, если ширина ткани будет 72 см?

При решении задач на обратно пропорциональную зависимость сначала нужно подробно разобрать с учащимися составление краткой записи пропорции. Например, краткая запись задачи про поезд сначала будет выглядеть вот так:

Скорость Время

45 км/ч - 4 ч

40 км/ч - х ч

Далее учащиеся устанавливают вид пропорциональной зависимости в задаче и показывают это с помощью разнонаправленных стрелочек. Так же учащиеся, опираясь на определение обратно пропорциональной зависимости, говорят, что отношение значений скорости должно быть равно обратному отношению значений времени движения поезда. Таким образом, краткая запись и пропорция будут выглядеть так:

С корость Время

45 км/ч - 4 ч

40 км/ч - х ч

Составлю и решу пропорцию:

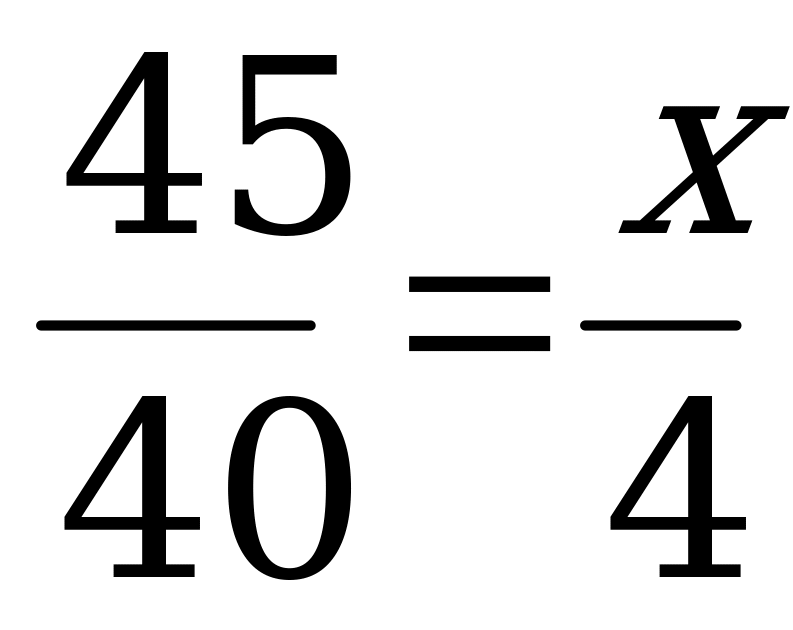
1. проверка полученного ответа:

а) решение задачи другим способом: например

Лыжник прошел 44 км за 4 ч. За сколько часов он пройдет 33 км при той же скорости движения?

Решение:

1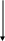 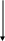способ:

44 км/ч - 4 ч

33 км/ч - х ч

Составлю и решу пропорцию:

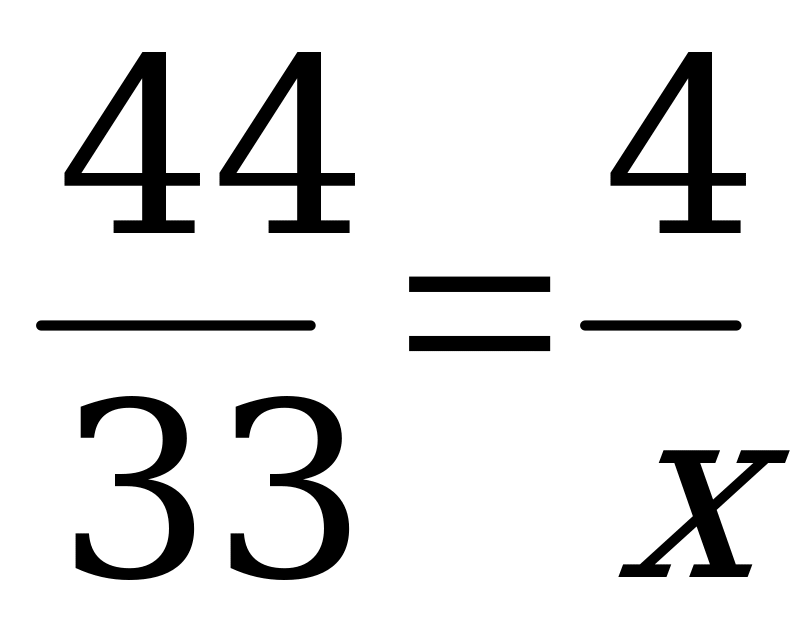
44х=33•4

Х=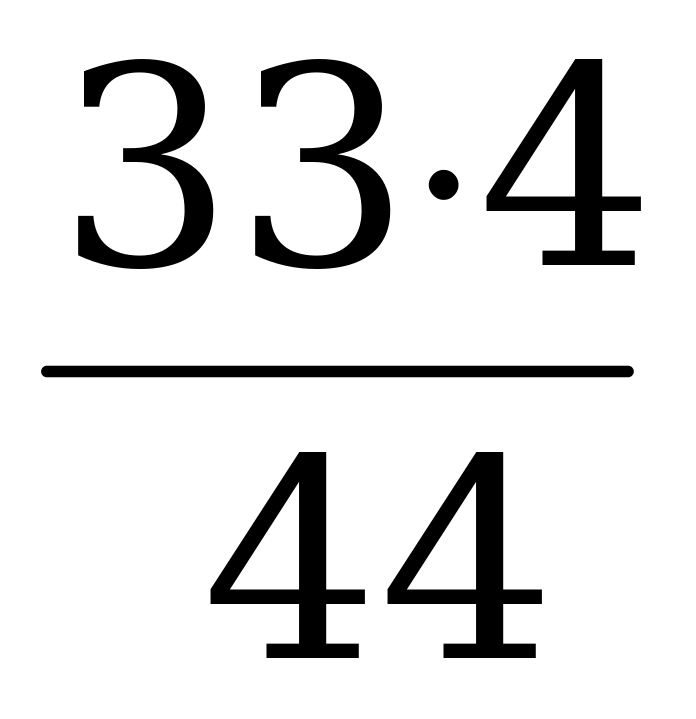

Х=3

3ч-время, за которое пройдет лыжник 33 км при той же скорости.

Ответ: 3 часа.

2 способ:

1) 44:4=11(км/ч)-скорость движения лыжника.

2) 33:11=3(ч)-время, за которое лыжник пройдет 33 км.

Ответ: 3 часа.

Б) прикидка ответа:

Учащиеся, опираясь на условие и смысл задачи, должны сделать вывод о полученном результате решения: может ли в ответе получиться величина большая или меньшая, чем задана; возможно ли по смыслу задачи такое значение.

3.Этап закрепления умения решать задачи с помощью пропорций.

После того, как учащиеся научились способу решения задач с помощью пропорций, необходимо закрепить это умение. Это можно сделать такими способами:

1)Дифференцированный подход к различным группам учащихся (работа по индивидуальным карточкам):

а) более сильным учащимся предлагается самостоятельное решение следующих задач:

 Карточка №1 .

Решите задачу двумя способами:

Решите задачу двумя способами:

1.В понедельник рабочий изготовил 63 детали, что составляет 18% недельного плана. Сколько деталей составляет недельный план?

2.Оконная замазка готовится из молотого мела и олифы, взятых в отношении 4:1.Сколько надо взять олифы для приготовления замазки, если мела взято 3,6 кг?

3.До обеда скосили 2,8 га, что составляет 24% площади луга. После обеда скосили еще 2,1 га. Сколько процентов луга скосили за день?

 Карточка №2 .

Решите задачу двумя способами:

1.Рационализаторы завода уменьшили массу детали с 60 кг до 51 кг. На сколько процентов уменьшилась масса детали?

2.Токарь изготовил за смену 644 детали, что составило 184% задания. Сколько деталей сверх задания изготовил токарь?

3.Пятна от чая удаляются смесью глицерина и нашатырного спирта, взятых в отношении 4:1. Сколько надо взять нашатырного спирта для пятновыводителя, если глицерина взято 50 г?

Б) среднеуспевающим учащимся предлагается решить задачи среднего уровня сложности:

 Карточка №1.

Реши задачу с помощью пропорции:

1.Когда изготовили 756 деталей, то выполнили план на 72%. Сколько деталей должны изготовить по плану?

2.на изготовление 8 деталей требуется 2г серебра. Сколько потребуется серебра на изготовление 14 таких деталей?

3.Автомашина прошла расстояние между двумя пунктами со средней скоростью 70 км/ч за 30 минут За сколько времени пройдет это расстояние автомашина. Если будет двигаться со скоростью 50 км/ч?

 Карточка №2.

Реши задачу с помощью пропорции:

1.Яблоки содержат 105 сахара. Сколько сахара содержится в 21,6 ц яблок?

2. Теплоход на подводных крыльях прошел расстояние между пристанями со средней скоростью 60 км/ч за 2,5 ч. За сколько времени пройдет это расстояние теплоход, если будет идти со скоростью 50 км/ч?

3.Сколько получится муки при размоле 12,5 т пшеницы, если масса муки составляет 80% массы зерна?

 Карточка №3.

Реши задачу с помощью пропорции:

1.Краеобметочная машина 0,6 м ткани обрабатывает за 2,16 мин. Сколько требуется времени, чтобы обметать 1,25 м такой ткани?

2.Когда сдали на элеватор 2,1 тыс.т пшеницы, то оказалось, что план сдачи зерна выполнен на 105%. Сколько тонн зерна надо было сдать по плану?

3.Всадник, двигаясь со скоростью 18 км/ч, преодолел некоторое расстояние за 1,5 ч. За какое время проедет это расстояние всадник, если уменьшит свою скорость на 3 км/ч?

 Карточка №4.

Реши задачу с помощью пропорции:

1.На выработку 2,4 т синтетического каучука расходуется 4,8 т спирта. Сколько понадобится спирта для получения 14,4 т каучука?

2.Сушеная вишня составляет 15% массы свежей. Сколько получится сушеной вишни из 160 кг свежей? Сколько надо взять свежей вишни, чтобы получить 90 кг сушеной?

 Карточка №5.

Реши задачу с помощью пропорции:

1.Из 300 кг семян льна получается 144 кг масла. Сколько масла получится из 175 кг семян льна?

2.4 комбайна могут убрать пшеницу с поля за 10 дней. За сколько дней уберут это поле 5 таких же комбайнов?

 Карточка №5.

Реши задачу с помощью пропорции:

1.Из коровьего молока можно получить 3,8 кг масла. Сколько масла можно получить из суточного надоя молока, если он составляет 15 кг?

2.Из каждых 9 саженцев принимаются 7. Сколько саженцев нужно посадить, чтобы принялись 30?

3.С включением в книгу цветных иллюстраций ее цена поднялась с 250 рублей до 331 рублей. На сколько процентов увеличилась цена книги?

 Карточка №6.

Реши задачу с помощью пропорции:

1.На 20 км пути автомашина расходует 3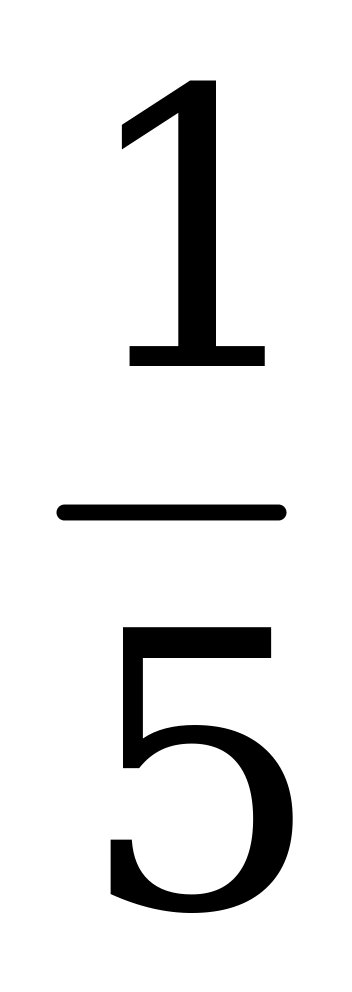 л горючего. Сколько горючего автомашина израсходует на 50 км пути?

2.Самолет пролетел расстояние между двумя аэродромами за 6 ч со скоростью 850 км/ч. За сколько времени пролетит это расстояние самолет, если увеличит свою скорость на 150 км/ч?

в) слабоуспевающим учащимся можно предложить решить задачи по готовой краткой записи с опорой на план решения задач с помощью пропорций

 Карточка №1.

Реши задачу с помощью пропорции:

1.Из 3 кг сырых зерен кофе получают 2,5 кг жареных зерен.

Сколько кг зерен надо взять, чтобы получить 1 кг жареных?

Р ешение:

3 кг - 2,5 кг

х кг - 1 кг

Составлю и решу пропорцию:

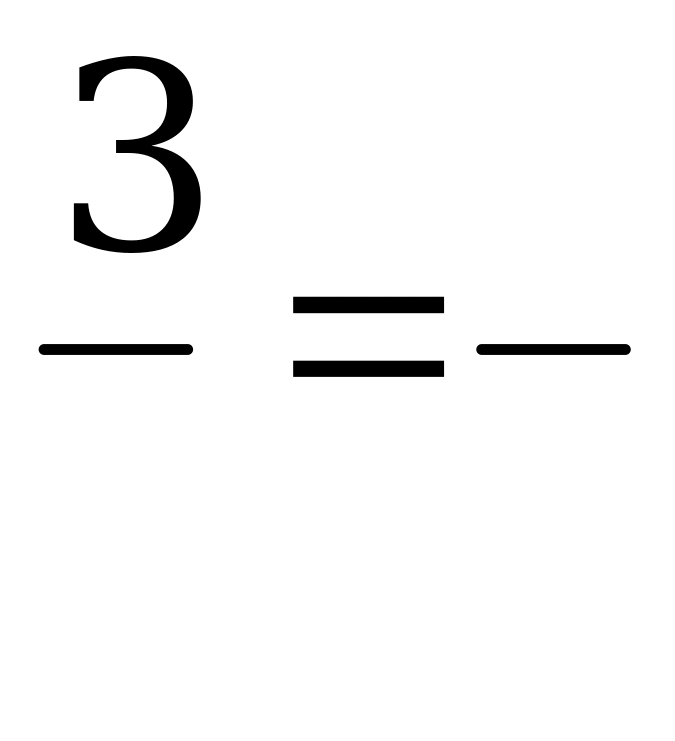
2.За 5 ч катер прошел 100 км. Какое расстояние пройдет катер за 3 ч при той же скорости?

Р ешение:

5 ч - 100 км

3 ч - х км

3.На решение уравнений Саша потратил 30% всего времени, которое он потратил на домашнее задание по математике. Сколько времени потратил мальчик на уравнения, если домашнюю работу по математике он выполнил за 30 минут?

 Карточка №1.

Реши задачу с помощью пропорции:

1.Из 100 кг коровьего молока получают 3,8 кг масла. Сколько масла можно получить из 15 кг молока?

Р 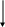ешение:

100 кг - 3,8кг

15 кг - х кг

Составлю и решу пропорцию:

2.При варке мяса из 100 г свежего получается 62 г вареного мяса. Сколько надо взять свежего мяса, чтобы получить 496 г вареного?

2)Решение задач различными способами:

На этом этапе закрепления умения решать задачи с помощью пропорций введение решения задач различными способами является необходимым для того, чтобы учащиеся смогли закрепить полученные навыки решения задач новым способом и для того, чтобы учащиеся смогли убедиться в преимуществах изученного способа решения задач по сравнению с другими. Это можно сделать на примере решения следующей задачи в форме «Закончи решение» (приложение 1-слайд 8,9):

Книга в переплете стоит 1200 рублей. Сколько процентов цена переплета составляет от цены книги в переплете, если книга без переплета стоит 900 рублей?

Решение:

1 способ:

1)1200-900=300(руб.)-стоимость переплета.

2)1200:100=12(руб.)-приходится на 1%.

3)300:12=25(%)-составляет цена переплета от цены книги в переплете.

2 способ:

1)1200-900=300(руб.)-стоимость переплета.

1200 руб. - 100%

300 руб. - х%

Составлю и решу пропорцию:

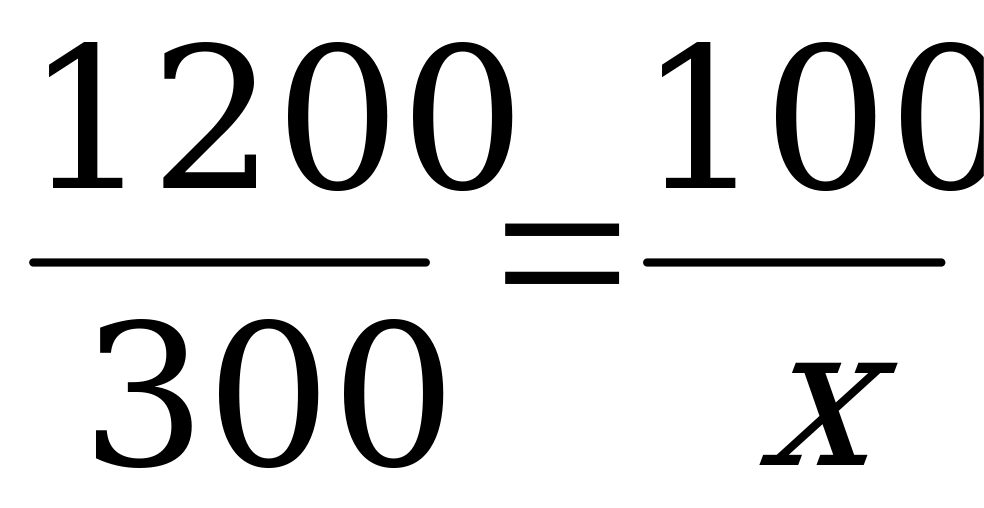
х•1200=300•100

х=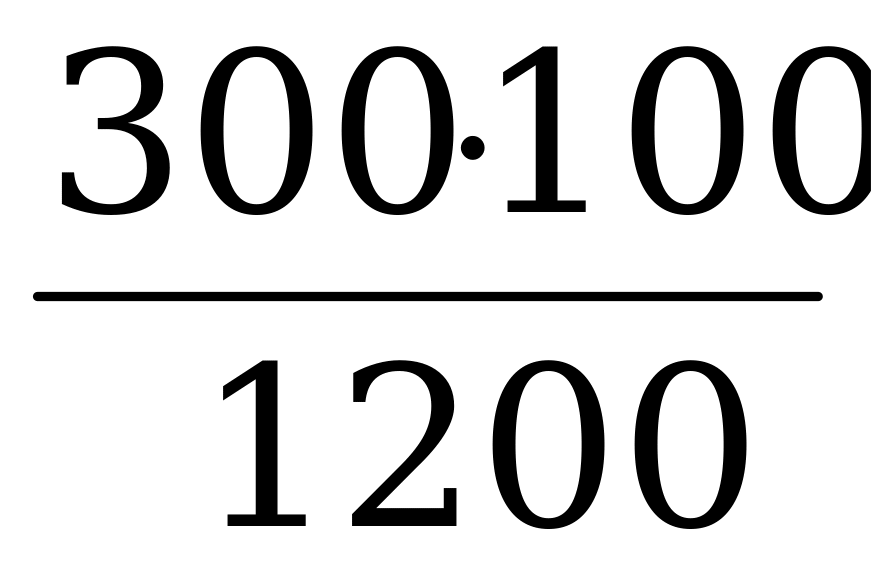

х=25

25%-составляет цена переплета от цены книги в переплете.

Ответ:25%.

1. Решение задач повышенной трудности:

Переходить к задачам повышенной трудности можно только тогда, когда учащимися хорошо усвоен план решения задач с помощью пропорций, когда отработаны навыки определения вида пропорциональной зависимости, составления пропорций.

Интересными для учащихся являются задачи-вопросы (приложение 1-слайд 10):

1.На покраску 10 м² требуется 1,2 кг краски. Хватит ли 1,5 кг краски на покраску пола комнаты, имеющей 3м в ширину и 4 м в длину?

2.На выработку 2,4 т синтетического каучука расходуется 4,8 т спирта. Хватит ли 28 т спирта для получения 14,4 т каучука?

3.Для изготовления 18 одинаковых приборов потребовалось 27 г платины. Хватит ли 35 г платины на изготовление 28 таких приборов?

Так же интересны задачи, представленные в виде таблицы (приложение 1-слайд 11):

1.Заполнить пустые клетки таблицы продажи завезенного в магазин картофеля в течение 4 дней:

	понедельник	вторник	среда	четверг	всего
Масса проданного картофеля, кг	900	2160			720
Процент от общей массы картофеля				20	100

2.Заполнить пустые клетки таблицы расхода имевшегося запаса угля в течение 5 месяцев:

	октябрь	ноябрь	декабрь	январь	февраль	всего
Количество израсходованного угля, т	189		237,6		199,8
Количество израсходованного запаса угля, %				22,5	18,5

Так же учащимся можно предложить составные задачи:

1.Расфасовали 0.9 т крупы, что составляет 46,8% всей крупы, привезенной в магазин. Сколько крупы надо еще расфасовать, чтобы она составляла 65% привезенной крупы?

2.Отрезок длиной 60 см разделили на 2 части. Найдите длины полученных отрезков, если их отношение равно 3:1.

3.Колхоз продал 80% хлопка 1-м сортом, 11% -2-м сортом и остальное-3-м сортом. Сколько тонн хлопка было продано 1-м и 2-м сортом в отдельности, если 3-мсортом было продано 432 т?

4.Колхоз сдал на элеватор 2000 т зерна, влажность которого 25%. Перед тем как засыпать зерно на длительное хранение, его сушат, доводя его влажность до 14%. Найти массу зерна, которую элеватор засыпает на длительное хранение. Ответ округлить до десятых.

Интересными и поучительными являются

З адачи о природе

(приложение 1-слайд 11, 12,13,14,15,16,17):

1.Черные лебеди составляют 40% от общего числа белых и черных лебедей, живущих в заповеднике. Сколько черных лебедей живет в заповеднике, если число белых лебедей на 21 больше числа черных?

2.Родиной белого журавля является наша страна. Из общего числа белых журавлей 60% обитает в Якутии и 0,4 – на реке Оби. Сколько всего сохранилось белых журавлей, если их в Якутии на 15 пар больше, чем на реке Оби?

3.Камбала живет 60 лет, что составляет 60% продолжительности жизни сома и 75% продолжительности жизни белуги, продолжительность жизни сазана равна 0,06 продолжительности жизни белуги. Сколько лет живет сом и сазан?

4.Число бурых медведей, сохранившихся в Казахстане, составляет 67%, а в Таджикистане 43% числа бурых медведей, сохранившихся в Киргизии. Сколько бурых медведей сохранилось в Киргизии, если в Таджикистане их на 350 больше, чем в Казахстане?

5.Определите число сахалинской кабарги (самые маленькие из оленей), если 35% их числа, сохранившихся на острове, на 270 особей меньше 0,8 того же числа.

6.Число сохранившихся в нашей стране белоплечих орланов составляет 50%, а число дроф 75% числа орланов-белохвостов. Сколько сохранилось указанных птиц, если число дроф на 1000 больше числа белоплечих орланов?

Можно посвятить целый урок таким задачам о природе, используя слайды с фотографиями этих животных, птиц, рыб.

Есть задачи, которые не столько сложны для учащихся в решении, сколько трудны в понимании условия и смысла задачи. Для таких задач можно предложить краткую запись в виде схемы. Например:

1.В совхозе площадь зерновых культур ранних сроков созревания составляет 25%, средних сроков созревания- 40% и поздних- 35% общей площади посевов зерновых культур. Сколько в отдельности занято этими культурами, если поздними культурами занято на 1200 га больше, чем ранними?

40 %

С редние сроки

25%

Р анние сроки

1200 га

П

35%

оздние сроки

О бщая площадь

100%

2.При помоле пшеницы получают 1% манной крупы, 32% муки высшего сорта, 22% кормовых отходов, а остальное составляет мука 1-го и 2-го сортов, причем масса муки 2-го сорта составляет 50% массы муки 1-го сорта. Сколько указанных продуктов и кормов можно получить из 45 т пшеницы?

1%

1-й сорт

2-й сорт

32%

22%

1-й сорт

100%

2-й сорт

50%

%

45 т

100%

3)Составление и преобразование задач, решаемых с помощью пропорций:

А) составление условия задачи по готовой краткой записи: учащимся предлагается во время устной работы составить условие задачи по готовой краткой записи (проверяется умение понимать краткую запись, соотносить друг с другом данные, составлять условие задачи, подходящее по смыслу),

Б) составление задачи по аналогии: учащимся предлагается самим составить краткую запись и по ней придумать условие задачи.

18