Урок "Суммаn-первых членов арифметической прогрессии"

07.02.2020

9 класс

Учитель: Сультимова Б.Б.

Карта самоконтроля. _____________________________________________

Карта самоконтроля. _____________________________________________

Критерии самооценки: «+» - материал знаю хорошо, умею применять при решении задач; «+ – » - материал знаю, но иногда делаю ошибки; «– + » - не знаю, но представляю решение; « – » - не знаю и не умею решать.

Устный счёт

• дайте определение арифметической прогрессии;
• найдите разность арифметической прогрессии если 25, 21, 17, . . .;
• найдите двенадцатый член арифметической прогрессии, если ее первый член равен 3, а разность 4.

3) Чему равна разность арифметической прогрессии: 1 1 ; 1 4; 1 7; …

Ответ: 3

4) Чему равна разность арифметической прогрессии: 3; 1 ; - 1 ; - 3 ; …

Ответ: - 2

Вычислите:

5) Найдите шестой член арифметической прогрессии: 3; 6 ; 9 ; …

Ответ: 1 8

6) Найдите пятый член арифметической прогрессии; если

Ответ: 17

«Не мог он ямба от хорея, как мы не бились отличить…» (Из романа Евгений Онегин).

Ямб

-мых ч

-дя с

«Мой д

Это интересно

е

я

а

-вил…»

а

ст-ных пр

8, …

6,

4,

2,

Хорей

о

-ет

-ря, мгл

-бо кр

е

-ю н

о

у

«Б

1;

3;

5;

7; …

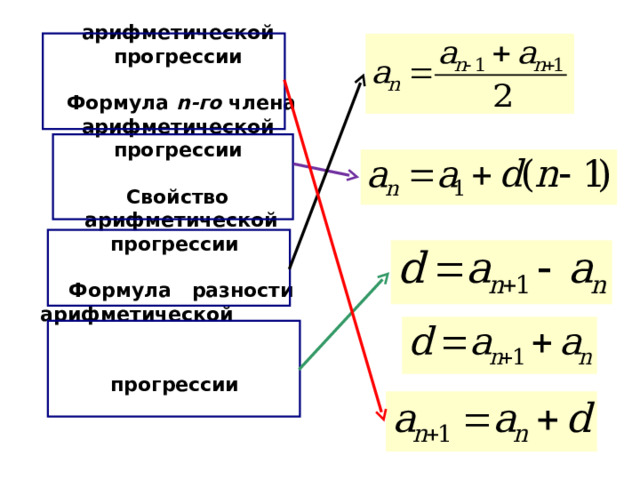
Определение арифметической прогрессии Формула n -го члена арифметической прогрессии Свойство арифметической прогрессии Формула разности арифметической прогрессии

З А Д А Н И Е .

Найти сумму первых ста натуральных чисел:

1 + 2 + 3 + 4 + 5 …+ 96 + 97+ 98 + 99 + 100

Эта задача связана с детскими годами замечательного

немецкого математика Карла Гаусса (1777–1855 гг.).

Когда ему было 9 лет, учитель задал эту задачу всему

классу, чтобы дети не мешали ему проверять

письменные работы учеников другого класса.

Через 1 минуту Карл произнес:

«Я уже решил…» – и сдал работу.

К концу урока сумму вычислили и остальные.

Карл Фридрих Гаусс

(1777-1855).

Давным-давно сказал один мудрец

Что прежде надо

Связать начало и конец

У численного ряда.

Задача очень непроста:

Как сделать, чтобы быстро

От единицы и до сто

Сложить в уме все числа?

Пять первых связок изучи,

Найдешь к решению ключи!

101

101

101

101

101 ▪ 50 = 5050

101

Тема урока.

Формула суммы первых n членов арифметической прогрессии.

Цели:

- вывести формулу суммы первых n членов арифметической прогрессии;

- выработать навыки, умения применения формул при решении задач;

- показать необходимость знания математики при решении жизненных задач.

Сумма арифметической прогрессии обозначается S n .

Сумма каждой пары членов прогрессии равна а 1 + а n . Всего таких слагаемых n/2.

Поэтому:

Но:

Пример 1

Найдите сумму первых 5 членов арифметической прогрессии (а n ) , если а 1 =6, а 5= 26 .

Дано:

Решение:

- арифметическая прогрессия

Пример 2

Найдите сумму первых 20 членов арифметической прогрессии: 1; 3,5; … .

Дано:

Решение:

- арифметическая прогрессия

Ответ: 495

Пример 2( по 1 формуле)

Найдите сумму первых 20 членов арифметической прогрессии: 1; 3,5; … .

Дано:

Решение:

- арифметическая прогрессия

Ответ: 495

№ 603 (а) – учебник, стр.151

Решение.

Ответ: S 60 =1800.

Дано: (а n ) - А.пр.

а 1 =3, а 60 =57.

Найти: S 60 .

Задача №1.

Родители ко Дню рождения своего сына Андрея решили купить и обновить ему мобильный телефон. Для этого они в первый месяц отложили 650 рублей, а в каждый последующий месяц они откладывали на 50 рублей больше, чем в предыдущий. Какая сумма будет у родителей Андрея через 10 месяцев?

Дано: Решение.

Найти:

Ответ:

Задача № 2 .

Джентльмен получил наследство. Первый месяц он истратил 1000$, а каждый следующий месяц он тратил на 500$ больше, чем в предыдущий. Каков размер наследства, если денег хватило на год такой безбедной жизни?

По формуле:

1. п.26 (формулы1,2; стр.155),

№№ 603(б), 604 (б), 605 .

2. Составить 2 задачи по теме «Арифметическая прогрессия в жизни и в быту» (на отдельном листочке с иллюстрацией) и решить.

Сегодня на уроке я:

1. Повторил…

2. Узнал…

3. Закрепил…

Рефлексия:

Оцените свою работу на уроке.

Перед вами карточка с изображением горы.

Если вы считаете, что хорошо усвоили тему урока, разобрались в решении задач , то нарисуйте себя на вершине горы.

Если осталось что-то неясно, нарисуйте себя ниже,

а слева или справа решите сами.

24