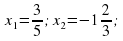Тема: Теорема Виета
Тип урока: комбинированный
Цели урока:
1. Обучающие: доказать теорему Виета, показать ее применение; рассмотреть различные задания на применение теоремы Виета, сформировать умение использовать эту теорему.
2. Развивающие: развивать умение наблюдать, сравнивать, обобщать и анализировать математические ситуации.
3. Воспитательные: воспитывать такие качества, как познавательная активность, самостоятельность. Упорство в достижении цели. Побуждать учеников к самоконтролю и самоанализу.
Оборудование: компьютер, проектор, слайдовая презентация, таблицы с уравнениями.
Ход урока
I. Вводно – мотивационная часть.
1. Организационный момент.
Учитель поверяет готовность класса к уроку и психологически настраивает детей на работу.
2. Актуализация опорных знаний.
Какую тему мы изучали на последних уроках?
Теоретические вопросы:
Определение квадратного уравнения. Привести пример.
Виды квадратных уравнений.
Алгоритм решения квадратных уравнений по формулам.
Вопросы для фронтального опроса:
Назвать корни уравнений:
х2 = 64
х2+3x = 0
у2 – 121 = 0
5x2 = 0
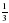 x 2 – 2 = 0
x 2 – 2 = 0
2. Указать коэффициенты квадратных уравнений:
2x2-5x+10=0
2+x+x2=0
5x2-4x=3
6x- x2=0
11-2x2=4x
3. Решить уравнение:
х2-6x+8=0 (2 и 4)
Я могу, не решая уравнения, сразу назвать корни. Как я это делаю?
II. Основная часть
1. Изучение нового материала.
1) Решить уравнения: (работают все в тетрадях и 3 человека у доски)
х2-2x-15=0
х2-10x+21= 0
х2 +5x +6 = 0
2) Все учащиеся заполняют таблицу:
| Уравнение | a | b | c | Корни | х1 + x2 | х1 *х2 |
|
х2-2x-15=0 х2-10x+21= 0
х2 +5x +6 = 0
|
|
|
|
|
|
|
Ученики формулируют выводы по таблице.
Историческая справка
Впервые эти выводы сделал Франсуа Виет (1540 – 1603 гг.)- французский математик.
Он стал одним из первых, кто стал обозначать числа буквами, что существенно развило теорию уравнений. Свои выводы Франсуа Виет сформулировал в виде теоремы и доказал ее. Использование этой теоремы позволяет экономить время при решении уравнений.
3) Доказательство теоремы.
Теорема: Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположны знаком, а произведение корней равно свободному члену.
Дано: x2+bx +c = 0, x1 и x2 – корни.
Доказать: x1 + x2 = - b,
X1 X2 = c.
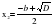
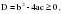 Доказательство:
Доказательство:
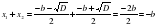
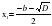
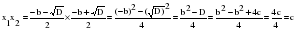
4) - Если квадратное уравнение не является приведенным, то как будет выглядеть теорема Виета?
После ответа учащихся на доску вывешивается плакат, а учащиеся делают запись в тетрадях.
Теорема Виета
По праву достойна в стихах быть воспета
О свойствах корней теорема Виета.
Что лучше, скажи, постоянства такого?
Умножишь ты корни – и дробь уж готова.
В числителе c, в знаменателе a
И сумма корней тоже дроби равна.
Хоть с минусом дробь эта, что за беда –
В числителе b, в знаменателе a?!
5) Физкультминутка.
Поднимает руки класс-это раз,
Повернулась голова – это два,
Руки вниз, вперед смотри – это три,
Руки в стороны пошире, развернули на четыре,
С силой их к плечам прижать – это пять.
Всем ребятам тихо сесть – это шесть.
2. Закрепление нового материала.
Все вместе решают уравнения.
x2+17x-18=0 x2-11x+18=0
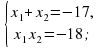
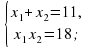
x1=-18, x2=1. x1=9, x2=2.
№ 965
Не используя формулу корней, найдите корни квадратного уравнения:
а) 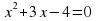 ( -4 и 1)
( -4 и 1)
б) 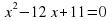 (11и 1)
(11и 1)
в) 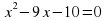 (10 и -1)
(10 и -1)
г) 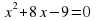 (1 и -9)
(1 и -9)
№ 968
Составьте квадратное уравнение, корнями которого являются числа:
а) 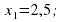
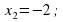
б)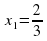 ;
; 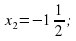
в)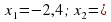 -1,5
-1,5
г)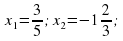
№ 970(а, б)
Пусть x1 и x2 – корни квадратного уравнения ax2+bx +c =0.
Найдите: а) b и c, если a =2, x1=3, x2= - 0,5;
б) a и c, если b= -1, x1=3,2= -4.
№ 972
При каких значениях параметра p произведение корней квадратного уравнения x2+3x+(p2-7p+12)=0 равно нулю?
III. Заключительная часть.
Рефлексия
- Что нового узнали на уроке?
- Как это будем использовать?
- Получилось ли реализовать цель, поставленную в начале урока?
- Что для вас было трудным на этом уроке?
Домашнее задание:
§24, №964, №967, №971.
Подведение итогов и выставление оценок.






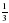 x 2 – 2 = 0
x 2 – 2 = 0
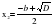
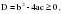 Доказательство:
Доказательство: 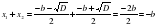
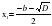
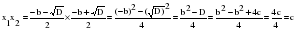
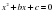
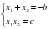
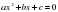
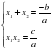
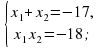
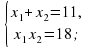
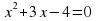 ( -4 и 1)
( -4 и 1)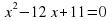 (11и 1)
(11и 1)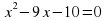 (10 и -1)
(10 и -1)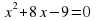 (1 и -9)
(1 и -9)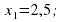
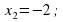
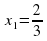 ;
; 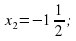
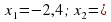 -1,5
-1,5