Урок в 9 классе по теме "Алгоритмы от "А" до "Я"

Карта самооценки

Домашнее задание

Карта самооценки

Домашнее задание

Задание № 1

Команды выполняются в порядке их записи

В названии этого типа алгоритма есть название части растения.

В алгоритмах этого типа никогда не может присутствовать блок условия.

Набор команд (указаний), выполняемых последовательно во времени друг за другом.

Действия алгоритма этого типа будут выполнятся до тех пор, пока выполняется заданное условие.

Примером алгоритма этого типа является алгоритм решения квадратного уравнения.

В алгоритм этого типа входит условие, в зависимости от выполнения или невыполнения которого реализуется та или иная последовательность команд.

Это такой алгоритм, в котором число повторений известно заранее.

Ключевое слова алгоритма этого типа - "повторять".

Задание № 2

1. Цикл - ДО: повторять до тех пор, пока условие выполняется.

2. К способам задания алгоритма относятся: словесный, письменный, устный, формульный, с помощью языков программирования.

3. Прямоугольник - фигура, в которой записывается условие.

4. Блок начала и конца алгоритма содержит неисполняемые команды.

5. Цикл - ПОКА: повторять, пока известно количество повторений.

6. Структура "Выбор" - это разновидность разветвляющегося алгоритма.

Задание № 3

1. Стоимость билета на электропоезд пригородного сообщения составляет а рублей. Школьникам предоставляется льгота b %. Вычислите стоимость проезда группы из k взрослых и n школьников?

2. Магазин «Малыш» закупает на оптовой базе наборы погремушек. Стоимость одного набора a рублей. Если общая сумма превышает 1000 рублей, то на эту часть суммы, которая превышает 1000 рублей, дается скидка b%. Сколько рублей магазин должен перечислить на счет оптовой базы при заказе n наборов?

1. Определите, чему равны значения a, b, c после выполнения алгоритма.

1. Из объявления фирмы, проводящей обучающие семинары:

«Стоимость участия в семинаре – k руб. с человека. Группам от организаций предоставляются скидки: от 4 до 10 человек – a%; более 10 человек – b%.»

Сколько рублей должна заплатить организация, направившая на семинар группу из n человек?

1. Известны годы рождения двух девочек - Маши и Кати. Определить, кто из них старше.

2. Сколько потребуется кафельных плиток квадратной формы со стороной a см, чтобы облицевать ими пол квадратной формы, сторона которого равна b м.

3. Акции предприятия распределены между государством и частными лицами в отношении a:b. Общая прибыль предприятия составила n млн. рублей. Какая сумма от этого пошла на выплату частным акционерам?

4. Из 30 листов цветной бумаги получается 12 ёлочных фонариков. Сколько таких фонариков можно изготовить из 80 листов бумаги?

5. Принтер печатает 1 страницу за a секунд. Сколько страниц можно напечатать на этом принтере за b минут?

6. В городе k жителей. N% от них - пенсионеры. Сколько человек составляет эта категория жителей?

7. Определите, чему равны значения А, K после выполнения алгоритма.

1. Известны два расстояния: одно в километрах, другое — в футах ( 1 фут 0,305 м ). Какое из расстояний меньше?

1. Определите, чему равны значения А, K после выполнения алгоритма.

Методический конструктор учебного занятия

Ход учебного занятия

Здравствуйте. (ПРИВЕТСТВИЕ)

На столах у вас лежат карточки зеленого цвета, переверните их, прочитайте, найдите человека, информация на карточке которого посвящена этому же, сядьте вместе.

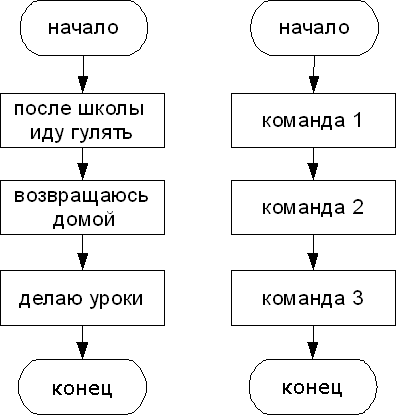
Линейный тип алгоритма

1.

2. Команды выполняются в порядке их записи

3. В алгоритмах этого типа никогда не может присутствовать блок условия.

4. Набор команд (указаний), выполняемых последовательно во времени друг за другом.

5.

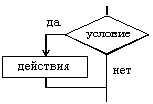
Разветвляющийся тип алгоритма

1.

2.

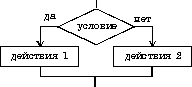
3. Примером алгоритма этого типа является алгоритм решения квадратного уравнения.

4. В алгоритм этого типа входит условие, в зависимости от выполнения или невыполнения которого реализуется та или иная последовательность команд.

5. В названии этого типа алгоритма есть название части растения.

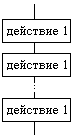
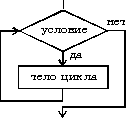
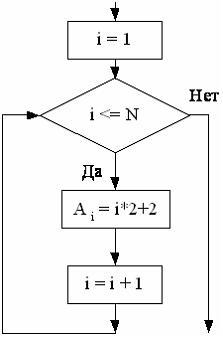
Циклический тип алгоритма

1.

2.

3. Это такой алгоритм, в котором число повторений известно заранее.

4. Ключевое слова алгоритма этого типа - "повторять".

5. Действия алгоритма этого типа будут выполнятся до тех пор, пока выполняется заданное условие.

После того, как все разделились на группы, доказывают, что сели правильно (зачитывают тексты с карточки). В случае ошибки - пересаживаются.

Итак, наш урок будет посвящен?... алгоритмам.

Тема ""

Какие цели мы должны достигнуть?

Повторить тему, ответить на вопросы, которые появились в процессе изучения темы, научиться структурировать знания по теме и т.д.

Прием "Согласен-не согласен" (каждая группа зачитывает любые два и выражают свое мнение) (Проверяется на экране, по эталону)

1. Цикл - ДО: повторять до тех пор, пока условие выполняется.

2. Цикл-ПОКА: повторять, пока известно количество повторений.

3. Прямоугольник - фигура, в которой записывается условие.

4. Блок начала и конца алгоритма содержит неисполняемые команды.

5. Структура "Выбор" - это разновидность разветвляющегося алгоритма.

6. К способам задания алгоритма относятся: словесный, письменный, устный, формульный, с помощью языков программирования.

ОЦЕНИВАНИЕ

Решение задач. На карточках задания на разные типы алгоритмов.

Группа "ЛА" решает по одной задаче на "РА" и "ЦА". Группа "ЦА" решает по одной задаче на ЛА" и "РА" и т.д.

Сначала каждый, потом в парах, потом - все.

После решения идут в соответствующие группы. представляют результаты работы. Возвращаются в свою группу, корректируют.

Выполняя письменную работу, отчёркивайте поля цветными карандашами, эти цвета имеют смысловую нагрузку:

• красный – «Проверьте, пожалуйста, всё и исправьте все ошибки»,

• зелёный – «Отметьте, пожалуйста, все ошибки, я сам исправлю»,

• синий – «Укажите количество ошибок, я их сам найду и исправлю».

ОЦЕНИВАНИЕ

1.  Стоимость билета на электропоезд пригородного сообщения составляет а рублей. Школьникам предоставляется льгота b %. Вычислите стоимость проезда группы из k взрослых и n школьников?

Протестируйте алгоритм для: а=198; в=50; к=4.n =12.

Решение. По условию стоимость билета для взрослого составляет 198 рублей. Для школьника предоставляется скидка 50% (полцены), поэтому стоимость билета равна 99 рублей. 4 взрослых билета будут стоить 792 рубля (умножаем 4 на 198. Для простоты счета умножаем 4 на 200 и вычитаем лишние 8), 12 школьных билетов будут стоить 1188 рублей (умножаем 12 на 99. Для простоты счета умножаем 12 на 100 и вычитаем лишние 12). Общая стоимость поездки составит 1980 рублей (складываем 792 и 1188).
Ответ: 1980.

2. Магазин «Малыш» закупает на оптовой базе наборы погремушек. Стоимость одного набора a рублей. Если общая сумма превышает 1000 рублей, то на эту часть суммы, которая превышает 1000 рублей, дается скидка 50%. Сколько рублей магазин должен перечислить на счет оптовой базы при заказе n наборов?

Решение.

1. 22 (n) ∙ 60 (a) = 1320 (руб.) стоимость 22 наборов

2. 1320 – 1000 = 320 (руб.) дается скидка

3. 1000 + 320 : 2 = 1160 (руб.) перечислит магазин

Ответ: 1160

3. Из объявления фирмы, проводящей обучающие семинары:

«Стоимость участия в семинаре – 1000 р. с человека. Группам от организаций предоставляются скидки: от 4 до 10 человек – a%; более 10 человек – b%.»

Сколько рублей должна заплатить организация, направившая на семинар группу из n человек?

Решение.

Т. к группа состоит из 7 человек, то фирма предоставляет скидку в 8%.

1) 100% - a% = 92% стоимость семинара для группы в 7 человек

2) 92% = 0,92

3) 7 ∙ 1000 ∙ 0,92 = 6440 рублей

Ответ: 6440

Известны годы рождения двух девочек - Маши и Кати. Определить, кто из них старше.

4.8. Известны два расстояния: одно в километрах, другое — в футах ( 1 фут 0,305 м ). Какое из расстояний меньше?

4. Из 30 листов цветной бумаги получается 12 ёлочных фонариков. Сколько таких фонариков можно изготовить из 80 листов бумаги?

5. Принтер печатает 1 страницу за a секунд. Сколько страниц можно напечатать на этом принтере за b минут?

6. В городе k жителей. N% от них - пенсионеры. Сколько человек составляет эта категория жителей?

7. Сколько потребуется кафельных плиток квадратной формы со стороной a см, чтобы облицевать ими пол квадратной формы, сторона которого равна b м.

8. Акции предприятия распределены между государством и частными лицами в отношении a:b. Общая прибыль предприятия составила n млн. рублей. Какая сумма от этого пошла на выплату частным акционерам?

9.

10.

11.

12.

Приём "Цветные поля".

Приём интерактивного обучения. Используется с целью создания психологически комфортной обстановки на уроке. Ученик, выполняя письменную работу, отчёркивает поля цветными карандашами, и эти цвета имеют смысловую нагрузку: красный – «Проверьте, пожалуйста, всё и исправьте все ошибки», – обращается он к учителю, зелёный – «Отметьте, пожалуйста, все ошибки, я сам исправлю», синий – «Укажите количество ошибок, я их сам найду и исправлю», чёрный – «Не относитесь, пожалуйста, серьёзно к этой работе, я её делал в спешке» и так далее.

Представляя задачу, на каждый шаг к доске, говорят что-то из теории алгоритмов.

Если останется время, по тестовой таблице нужно восстановить алгоритм.

ОЦЕНИВАНИЕ

ОЦЕНИВАНИЕ

Рефлексия "Рюкзак".

Прием рефлексии используется чаще всего на уроках после изучения большого раздела. Суть - зафиксировать свои продвижения в учебе, а также, возможно, в отношениях с другими. Рюкзак перемещается от одного ученика к другому. Каждый не просто фиксирует успех, но и приводит конкретный пример. Если нужно собраться с мыслями, можно сказать "пропускаю ход".

Пример.

• я научился составлять план текста

• я разобрался в такой-то теме

• я наконец-то запомнил, чем причастие отличается от деепричастия и т.д.

Домашнее задание: составить как можно больше вопросов, используя информацию из таблицы. Записать вопросы в тетрадь.

МОУ Школа № 1 г. Черемхово

Конструирование урока информатики на основе системно-деятельностного подхода с учетом ФГОС

Муниципальный семинар учителей информатики

Программа семинара

Время

ФИО

10.00 - 10.15

Тема

Чепурыгина Н.А.,

10.15 - 10.25

методист МУ ТРЦ г. Черемхово

Григорьева О.В., учитель ИиИКТ

10.25 - 10.40

Типология уроков на системно-деятельностной основе по ФГОС

10.40 - 11.15

Надина А.А., заместитель директора по НМР

Интерактив «Методическая разминка»

Учителя МО

11.15 - 11.55

Проектирование урока на системно-деятельностной основе

11.55 - 12.10

Григорьева О.В., учитель ИиИКТ

Практикум по проектированию урока на системно-деятельностной основе

Григорьева О.В., учителя МО

Урок ИиИКТ в 9 классе

12.10 - 13.00

Расширенный анализ урока

Степанова В.В. (видеоурок)

13.00 - 13.10

Работа с экспертной картой урока

Рефлексия. Подведение итогов семинара

«Сведений науки не следует сообщать учащемуся, но его надо привести к тому, чтобы он сам их находил, самодеятельно ими овладевал. Такой метод обучения наилучший, самый трудный, самый редкий. Трудностью объясняется редкость его применения. Изложение, считывание, диктовка против него детская забава…»

Адольф Дистервег

Технологическая карта урока (общая часть)

Тема

Цель

Планируемые результаты

Основные понятия

Предметные: знать, уметь, понимать, применять

Метапредметные:  Регулятивные УУД,

Межпредметные связи

Средства обучения:

Коммуникативные УУД, Познавательные УУД:

Формы урока

  дидактические

Личностные

  программные

фронтальная, индивидуальная, парная, групповая

Методы обучения, пед. технологии

технические

«Если бы в кабинете у врача, юриста или дантиста одновременно собрались 30 человек с разными желаниями и потребностями, а некоторые, не имея желания там находиться, постоянно мешали бы ему работать, а врач, юрист или дантист (без ассистента), должен был бы в течение 9 месяцев, применяя все свое мастерство, добиться высоких профессиональных результатов, вот тогда, возможно, он бы получил некоторое представление о работе школьного учителя»

Дональд Д. Куинн, перевод с английского

Алгоритмы от "А" до "Я"

Еще не все колеса изобретены: мир слишком удивителен, чтобы сидеть сложа руки.

Ричард Брэнсон

Кто пассивно ждёт – в конце концов получает ожидаемое, но только то, что осталось после тех, кто действовал энергично.

Авраам Линкольн

Карта самооценки

• Знаю теорию алгоритмов
• Умею применять базовые алгоритмические структуры при решении учебных задач
• Умею тестировать алгоритмы
• Умею взаимодействовать со сверстниками в группе

2

1

0

2

1

0

2

1

0

2

1

0

2

1

Знаю, умею

0

Испытываю затруднения (нуждаюсь в помощи)

Знания, умения отсутствуют

Задание № 2

• Цикл - ДО: повторять до тех пор, пока условие выполняется.
• К способам задания алгоритма относятся: словесный, письменный, устный, формульный, с помощью языков программирования.
• Прямоугольник - фигура, в которой записывается условие.
• Блоки начала и конца алгоритма содержат неисполняемые команды.
• Цикл - ПОКА: повторять, пока известно количество повторений.
• Структура "Выбор" - это разновидность разветвляющегося алгоритма.

-

-

-

+

-

+

«ЛА»

«ЦА»

«РА»

Каждая группа из списка задач решает две - на типы алгоритмов, не соответствующие типам своей группы

• «РА» «ЦА»
• «РА»
• «ЦА»

• «ЦА» «ЛА»
• «ЦА»
• «ЛА»

• «РА» «ЛА»
• «РА»
• «ЛА»

Рекомендации к заданию № 3

• Выполняя задание, делайте на полях пометки цветными стикерами. Цвета имеют смысловую нагрузку (обращение к учителю):
• оранжевый– «Проверьте, пожалуйста, всё и исправьте все ошибки»,
• голубой– «Отметьте, пожалуйста, все ошибки, я сам исправлю»,
• желтый– «Укажите количество ошибок, я их сам найду и исправлю».

0 B:=B-1 30 + A:=A*2+1 B:=3-1=2 20 + B:=2-1=1 A:=2*2+1=5 10 + A:=5*2+1=11 B:=1-1=0 00 - A:=11*2+1=23" width="640"

А=2

В=3

В0

B:=B-1

30 +

A:=A*2+1

B:=3-1=2

20 +

B:=2-1=1

A:=2*2+1=5

10 +

A:=5*2+1=11

B:=1-1=0

00 -

A:=11*2+1=23

Вопросительные слова

Как?

Основные понятия темы

Алгоритм

Что?

Свойства алгоритма

Где?

Типы алгоритма

Почему?

Линейный

Сколько?

Разветвляющийся

Откуда?

Какой?

Циклический

Дискретность

Зачем?

Каким образом?

Понятность

Точность

Какая взаимосвязь?

Из чего состоит?

Результативность

Каково назначение?

Массовость

Урок можно считать результативным, если:

• Цели урока задаются с тенденцией передачи функции от учителя к ученику.
• Учитель систематически обучает детей осуществлять рефлексивное действие (оценивать свою готовность, обнаруживать незнание, находить причины затруднений и т.п.)
• Используются разнообразные формы, методы и приемы обучения, повышающие степень активности учащихся в учебном процессе.
• Учитель владеет технологией диалога, обучает учащихся ставить и адресовать вопросы.
• Учитель эффективно (адекватно цели урока) сочетает репродуктивную и проблемную формы обучения, учит детей работать по правилу и творчески.
• На уроке задаются задачи и четкие критерии самоконтроля и самооценки (происходит специальное формирование контрольно-оценочной деятельности у обучающихся).
• Учитель добивается осмысления учебного материала всеми учащимися, используя для этого специальные приемы.
• Учитель стремиться оценивать реальное продвижение каждого ученика, поощряет и поддерживает минимальные успехи.
• Учитель специально планирует коммуникативные задачи урока.
• Учитель принимает и поощряет, выражаемую учеником, собственную позицию, иное мнение, обучает корректным формам их выражения.
• Стиль, тон отношений, задаваемый на уроке, создают атмосферу сотрудничества, сотворчества, психологического комфорта.
• На уроке осуществляется глубокое личностное воздействие «учитель – ученик» (через отношения, совместную деятельность и т.д.).

Показатели владения педагогом системно-деятельностными технологиями обучения:

• имеет гуманистическую позицию по отношению к каждому ребенку;
• системно видит предметный курс в иерархии внутрипредметных и межпредметных связей и отношений;
• проектирует цели курса, темы, урока, исходя из личностных, метапредметных и предметных результатов;
• создает мотивационно-целевое пространство уроков на основе развития личностных потребностей учеников;
• организует поисковую, проблемную, проектную деятельность детей;
• организует учебное сотрудничество детей при решении учебных задач на основе демократического общения;
• организовывает самоконтроль и самооценку учащимися своей деятельности в соответствии с выработанными критериями;
• владеет способами организации рефлексии, аутентичными формами оценивания;
• осуществляет самоанализ собственной педагогической деятельности с позиции достижения личностных, метапредметных и предметных результатов.

Тип урока

Вид урока

3. Урок когнитивного типа – ориентирован на структуру учебной деятельности и виды познавательной деятельности

1 . Урок постановки учебной задачи - постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимся, и того, что еще неизвестно

2. Урок информационного поиска - поиск и выделение необходимой информации

3. Аналитический урок - анализ объектов с целью выделения признаков (существенных, несущественных), выбор оснований и критериев для сравнения, сериации, классификации объектов, установление причинно-следственных связей

4. Урок моделирования – преобразование объекта из чувственной формы в модель, где выделены существенные характеристики объекта (пространственно-графическую или знаково-символическую) и преобразование модели с целью выявления общих законов, определяющих данную предметную область

Тип урока

Вид урока

3 . Урок когнитивного типа – ориентирован на структуру учебной деятельности и виды познавательной деятельности

5 . Урок - доказательство - построение логической цепи рассуждений, доказательство; выдвижение гипотез и их обоснование

6. Урок отработки освоенного способа действия - выбор наиболее эффективных способов решения задач в зависимости от конкретных условий

7. Урок – обобщение - синтез как составление целого из частей, в том числе на основе самостоятельного достраивания, восполнение недостающих компонентов; подведение под понятия, выведение следствий

8. Урок рефлексии - рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности

9. Урок постановки и решения проблем

3-2-1

Необходимо найти:

• 3 плюса рассматриваемого объекта,
• 2 минуса и
• внести 1 предложение по его модернизации

Мы не учим их; мы создаем условия, в которых они учатся.

С. Паперт

Таблица самооценки конспекта урока

№

1

Критерий

2

Соответствие структуры урока положениям системно-деятельностного подхода: наличие мотивационного, операционального и рефлексивно - оценочного этапов

1

2

Участие обучающихся в целеобразовании, планировании, поисковой деятельности по открытию нового знания, осуществление самоконтроля, самооценки, корректирующих действий

3

3

Направленность деятельности обучающихся на формирование универсальных учебных действий: познавательных, регулятивных, коммуникативных, личностных

4

4

Технологичность структуры урока: диагностичность целей и задач, адекватность всех компонентов целям урока

5

5

Оптимальный отбор содержания: ценностные ориентиры, научность, доступность, отражение межпредметных связей, практическая направленность, достаточность и необходимость объема для изучения, использование ИКТ

6

Наличие разных форм организации учебной деятельности (включая индивидуальную и групповую)