| Урок 99 | 22.04. |
| Биссектрисы треугольника и отношение площадей. |
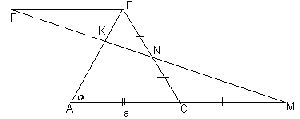
Рис. 1
1. Разбор с/р.
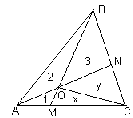
Рис. 2
2. Проверка д/з: вопросы по доказательству следствий из теоремы Чевы? №160 [Cм. рис. 1; доп. построение и подобие, либо по теореме Менелая: |BK| : |KA| = 1 : 2; S
BKN =
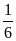
S
ABC;
SAKNC = 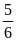 SABC
SABC]; №165 [Cм. рис. 2; проведем [CO]:
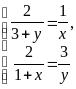
Û
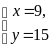
;
SABC = 30 дм2]
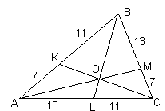
Рис. 3
3) [См. рис. 3; для того, чтобы построить искомую точку О достаточно разделить стороны АВ, ВС и СА треугольника АВС соответственно точками K, M и L так, чтобы |AK| : |BK| = 7 : 11; |BM| : |CM| = 13 : 7; |CL| : |AL| = 11 : 13. Тогда, по теореме Чевы, отрезки AN, BL и CK пересекутся в одной точке, которая и будет искомой]
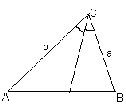
Рис. 4
Некоторые задачи на вычисление отношения площадей связаны с биссектрисами треугольника. Они имеют свою специфику.
3. Упражнения. 1) (устно с записями на доске) Рассмотрим DАВС, в котором проведена биссектриса CL (см. рис. 4). А) Найдите SACL : SBCL, если |BC| = a; |AC| = b [SACL : SBCL = b : a. Разобрать два способа]
Значит, свойство биссектрисы треугольника можно доказывать с помощь площадей!
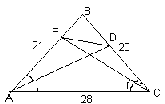
Рис. 5
Б) Найдите
SACL, если |AC| = 3; |BC| = 2; ÐACB = 30°
[SACL = 0,6SABC = 0,9]
В) Найдите SBCL, если a = 6; b = 9; c = 5 [SBCL = 0,4SABC = 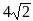 ]
]
2) Пос.: №151 (на доске и в тетрадях).
[См. рис. 5; 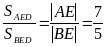 ;
; 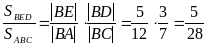 Þ
Þ 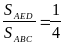 ]
]
Домашнее задание: Пос.: №113; №149; №169. Диаметр PQ и перпендикулярная ему хорда MN пересекаются в точке A. Точка C лежит на окружности, а точка B – внутри окружности, причем (BC) || (PQ) и |BC| = |MA|. Из точек A и B опущены перпендикуляры AK и BL на прямую CQ. Докажите, что треугольники ACK и BCL равновелики.
71








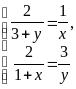 Û
Û