Условная вероятность. Правило умножения. Независимые события (8 класс)

Условная вероятность, умножение вероятностей, независимые события.

Условная вероятность. Правило умножения. Независимые события.

Учитель Коржева Е.А.

8 класс

(5ч)

1. Ведение словаря новых терминов (глоссарий)

№ урока

Дата проведения

Тема урока

Название

Определение, правило, формула, свойства, виды, элементы, … (допустимо на описательном уровне)

Примеры, основные

типы задач

Основное содержание:

Условная вероятность. Правило умножения вероятностей. Представление случайного эксперимента в виде дерева. Независимые события.

Основные виды деятельности обучающихся:

Осваивать понятия: правило умножения вероятностей, условная вероятность, независимые события, дерево случайного опыта.

Решать задачи на определение и свойства независимых событий.

Решать задачи на поиск вероятностей с использованием дерева случайного опыта.

1.Условная вероятность

2.Правило умножения вероятностей

Вероятность события А при условии, что событие В произошло, называется условной вероятностью события А при условии В. Обозначается эта вероятность Р(А|В)

Вероятность пересечения событий А и В равна произведению вероятности одного из них и условной вероятности другого Р(АВ)= Р(В)* Р (А|В)

Рассмотрим пример

В городе 48% населения-женщины.Среди женщин 55% работают.Какую часть жителей города составляют работающие женщины?

Решение:( вспомним как найти часть от числа,выраженную дробью) Пусть в городе-х жителей,тогда 0,48* х жителей -это женщины,а работающие женщины составляют –

0,55* 0,48* х .

Значит , доля работающих женщин равна (0,55* 0,48* х)\х=0,48*0,55=0,264

В этой задаче можно вопрос задатьпо другому.Какова вероятность,что выбранный житель этого города окажется работающая женщина?

Пусть В= выбранный житель окажется женщина

А= выбранный житель работает

Тогда Р(В)=0,48 ,вероятность события А неизвестна и Р (А|В)=0,55 эта условная вероятность условия А при условии В. Р(АВ)= Р(В)* Р (А|В)=0,48*0,55=0,264

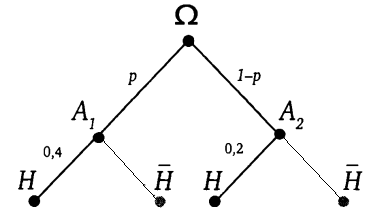
1.В некотором случайном эксперименте могут наступить события А и В.Найдите вероятность

события АВ,если :

а) Р(А)=0,4 , Р (В|А)=0,3

б) Р(В)=0,8 , Р (А|В)=0,6

Решение:

а) Р(АВ)= Р(А)* Р ( В|А )

Р(АВ)=0,4*0,3=0,12

б) Р(АВ)= Р(В)* Р (А|В)

Р(АВ)=0,8*0,6=0,48

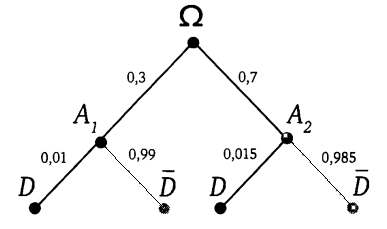
2. В некотором случайном эксперименте могут наступить события А и В.Найдите условную вероятность Р (А|В), если

а) Р(В)=0,25 , Р(АВ)=0,23

б) Р(В)=0,17 , Р(АВ)=0,068

Решение:

Р(АВ)= Р(В)* Р (А|В) Отсюда выразим условную вероятность,получаем

Р (А|В)= Р(АВ)\ Р(В)

а) Р (А|В)=0,23:0,25=0,92

б) Р (А|В)=0,068:0,17=0,4

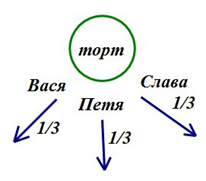
Пример 1. Велосипедист едет по парковой дорожке (рис. 11) и планирует выехать из парка через один из пяти выходов (А, В, С, D или Е)

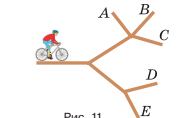
Велосипедист едет только вперед и на каждой развилке случайным образом выбирает одну
из дорожек, по которой еще не ехал. Какова вероятность того, что велосипедист покинет парк:
а) через выход А;
б) через выход Е?
Желательный результат обсуждения. Начальное состояние, когда велосипедист не проехал ни один из перекрестков, изобразим точкой S

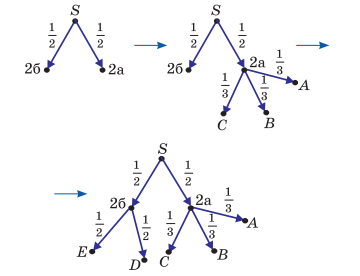
Подпишем получившиеся вероятности

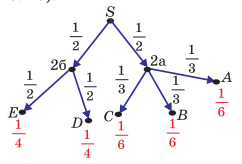
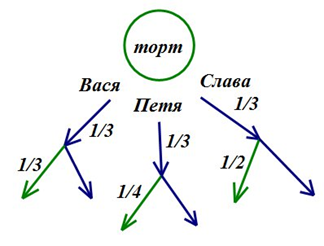
Пример 2. Пусть известно, что выходы D
и С ведут к пруду. Найдите вероятность того, что
велосипедист выедет из парка к пруду.

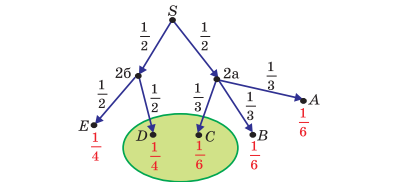
Желательный результат обсуждения.
На рисунке обведем элементарные события, благоприятствующие событию «велосипедист выедет к пруду»

Искомая вероятность равна сумме вероятностей наступления этих исходов, то есть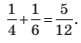

Можно сформулировать общее правило нахождения вероятностей событий с помощью дерева. Оно получается из правила сложения вероятностей элементарных событий.

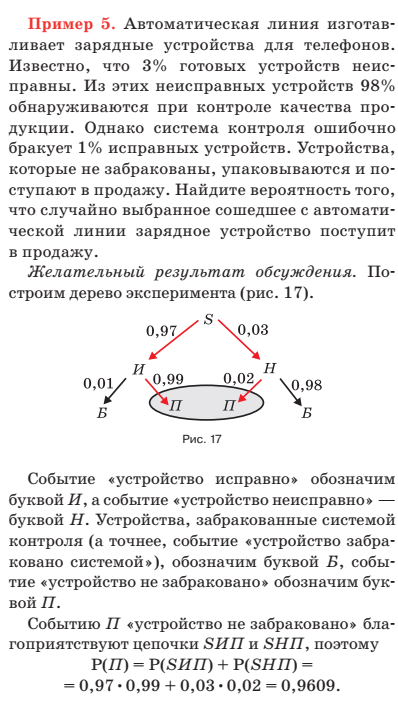
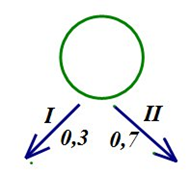
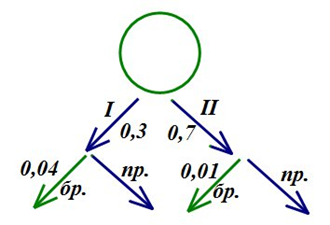
1)Два стрелка независимо друг от друга стреляют по

мишени. Вероятность попадания первого стрелка равна 0,7; второго-0,6. Какова вероятность двух попаданий, если каждый сделал по одному выстрелу.

Решение:

Т.к. выстрелы двух стрелков независимы друг от друга, то вероятность двух попаданий равна произведению вероятностей. Получаем Р(А)=0,7 Р(В)=0,6,то Р(АВ)=0,7* 0,6=0,42

2)

Два стрелка независимо друг от друга стреляют по

мишени. Вероятность попадания первого стрелка равна 0,7; второго-0,6. Какова вероятность ровно одного попаданий, если каждый сделал по одному выстрелу.

Решение:

Мишень может быть поражена ровно раз в двух случаях: 1) первый стрелок попал, и второй стрелок не попал

2) не попал первый и попал второй стрелок

Тогда вероятность Р=0,7*0,4+0,3*0,6=0,46

3) Три стрелка независимо друг от друга стреляют по одной и той же мишени, вероятность попадания первого 0,9; для второго-0,7; для третьего-0,6.

Найдите вероятность того, что:

1) все три попали в мишень

2)все три промахнулись

3) хотя бы один попал в цель, если каждый сделал по одному выстрелу.

Решение:

Аи А1,В и В1,С и С1 противоположные события

1. Р(А)=0,9 Р(В)=0,7 Р(С)=0,6

Р(АВС)=0,9*0,7*0,6=0,378

1. Р(А1) =0,1 Р(В1) =0,3 Р(С1) =0,4

Р(А1В1С1) =0,1*0,3*0,4=0,012

1. Вероятность, того, что все три стрелка промахнулись равна 0,012, то противоположное событие хотя бы один стрелок попал в цель равна

Р=1-0,012=0,988

3.Дерево случайного опыта

4

4.Независимые события

Дерево случайного опыта или дерево вероятностей — удобный инструмент решения задач,
который позволяет рассматривать составной эксперимент как бы «по частям», мысленно расположить случайные события во времени или разбить на этапы. Объясним, как строить дерево
эксперимента, на примере.

События А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Для независимых событий имеет место формула Р(АВ)= Р(А)* Р(В)

*

1. Практикум по теме

«Дерево случайного опыта»

1)Трое друзей Вася, Петя и Слава купили торт, и решили его съесть. Они разделили торт на три равных части. Внезапно появился четвертый друг Коля, и друзья решили отрезать ему по кусочку от своей доли. Вася отрезал 1/3 от своего куска, Петя 1/4, а Слава – половину. Какую часть всего торта получил в итоге Коля?

Изобразим ситуацию, описанную в задаче в виде такой схемы:

Сначала торт разрезали на три равные части, и каждому из трех друзей досталось по 1/3 торта.

Затем пришел Коля и каждый мальчик отрезал ему соответствующую часть своего куска:

Чтобы найти дробь от числа, нужно число умножить на эту дробь. То есть Вася отдает Коле часть торта, Петя -   часть торта, а Слава  часть торта.

В итоге Коля получит   часть тортa.

Ответ:13\36 торта

2)Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 30% этих стекол, а вторая – 70%. Первая фабрика выпускает 4% бракованных стекол, а вторая – 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Изобразим ситуацию в виде дерева вероятностей:

Все стекла делятся на те, которые выпускает первая фабрика и на те, которые выпускает вторая:

Стекла, которые выпускает каждая фабрика делятся на бракованные и пригодные. Из стекол, которые выпускает первая фабрика 4% бракованных, и из тех, которые выпускает вторая – 1% бракованных:

Нас интересуют бракованные стекла, которые выпускаются первой или второй фабрикой. Найдем, какую часть эти стекла составляют от всех стекол:

Ответ: 0,019

3)Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц из этих двух хозяйств. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

Решение.

События «яйцо поступило из первого хозяйства» и «яйцо поступило из второго хозяйства» назовем A1 и A2 соответственно. Обозначим буквой p искомую вероятность события A1 и нарисуем дерево.

Получаем:
P(H)=0,4+(1-p)0,2.
По условию эта величина равна 0,35.
Тогда
0,4p+0,2(1-p) =0,35,
откуда 0,2p=0,15 и, значит, p=0,75.

Ответ: 0,75.


4)Две фабрики одной фирмы выпускают одинаковые мобильные телефоны. Первая фабрика выпускает 30% всех телефонов этой марки, а вторая — остальные телефоны. Известно, что из всех телефонов, выпускаемых первой фабрикой, 1% имеют скрытые дефекты, а у выпускаемых второй фабрикой — 1,5%. Найдите вероятность того, что купленный в магазине телефон этой марки имеет скрытый дефект.

Решение.

Введем обозначения для событий:
A1 = {телефон выпущен на первой фабрике},
A2 = {телефон выпущен на второй фабрике},
D = {телефон имеет скрытый дефект}.
По условию задачи составим дерево и найдём необходимые вероятности.

P(D)=0,3 *0,01+0,7*0,015=0,003+0,0105=0,0135.

Ответ: 0,0135