В мире фракталов

Муниципальное бюджетное общеобразовательное учреждение «Кочкуровская средняя общеобразовательная школа»

Дубенского муниципального района

Республики Мордовия

Проектная работа

Автор: Кияйкин Алексей,

ученик 11 класса

Руководитель:

Бровцева Анна Викторовна,

учитель математики и информатики

2017

Оглавление

Введение………………………………………………………..………………….3

1. Теоретическая глава « Из истории фракталов»

1.1.История возникновения…………………………….………...………………6

1.2. Классификация фракталов……………………….…………………………..8

1.3. Фрактальная геометрия природы……………..…….……………………...11

1.4. Применение фракталов…...………………………………………………...13

2. Практическая глава «Обзор программного обеспечения генерации фракталов»……………………………………………………………………….18

2.1. Моделирование фракталов на языке Pascal ABC…………………………18

2.2. Построение фрактала в программе Fractal Explorer……………………...21

2.2. Построение фрактала в программе Incendia ……………………………..24

Заключение ………………………………………………………………………30

Список использованных источников…………………………………………...32

Введение

Актуальность исследования.

Слово “фрактал” — это что-то, о чем много людей говорит в наши дни, от ученых до учеников средней школы. Оно появляется на обложках многих учебников математики, научных журналов и коробках с компьютерным программным обеспечением. Цветные изображения фракталов сегодня можно найти везде: от открыток, футболок до картинок на рабочем столе персонального компьютера. Итак, что это за цветные формы, которые мы видим вокруг?

Большинству людей казалось, что геометрия в природе ограничивается такими простыми фигурами, как линия, круг, многоугольник, сфера и т.д. Как оказалось многие природные системы настолько сложны, что использование только знакомых объектов обычной геометрии для их моделирования представляется безнадежным. Как, к примеру, построить модель горного хребта или кроны дерева в терминах геометрии? Как описать то многообразие биологических разнообразий, которое мы наблюдаем в мире растений и животных? Как представить всю сложность системы кровообращения, состоящей из множества капилляров и сосудов и доставляющей кровь к каждой клеточке человеческого тела? Представить строение легких и почек, напоминающие по структуре деревья с ветвистой кроной?

Фракталы - подходящие средства для исследования поставленных вопросов. Нередко то, что мы видим в природе, интригует нас бесконечным повторением одного и того же узора, увеличенного или уменьшенного в несколько раз. Изучение фракталов открывает замечательные возможности, как в исследовании бесконечного числа приложений, так и в области математики. Применение фракталов очень обширно! Ведь эти объекты настолько красивы, что их используют дизайнеры, художники, с помощью них в графике рисуются многие элементы деревья, облака, горы и т.д.

В своей работе я тоже решил «прикоснуться» к миру прекрасного.

Цель работы: знакомство и изучение мира фракталов, их применения.

Задачи:

• знакомство с понятием, историей возникновения и исследованиями Б.Мандельброта, Г. Коха, В. Серпинского и др.;

• знакомство с различными видами фрактальных множеств;

• изучение научно-популярной литературы по данному вопросу, знакомство с научными гипотезами;

• нахождение подтверждения теории фрактальности окружающего мира;

• изучение применения фракталов в других науках и на практике;

• смоделировать фракталы при помощи различных программных средств.

Основополагающий вопрос работы: показать, что математика не сухой, бездушный предмет, она может выражать духовный мир человека в отдельности и в обществе в целом.

Объект исследования: фракталы в математике и в реальном мире.

Предмет исследования: фрактальная геометрия.

Гипотеза: все, что существует в реальном мире, является фракталом.

Методы исследования: сравнительный анализ, синтез, моделирование.

Результат исследования: разработка программ построения фракталов.

Теоретическая и практическая значимость: использование программ построения фракталов на уроках и факультативных занятиях по математике, информатике и искусству.

Ожидаемые результаты: В ходе работы, я смогу расширить свои знания в области математики, увидеть красоту фрактальной геометрии, начать работу по созданию своих фракталов.

Итогом работы будет создание компьютерной презентации и программ на языке программирования Паскаль по созданию фракталов.

1. Теоретическая глава «Из истории фракталов»

1.1. История возникновения

Понятия "фрактал" и "фрактальная геометрия" возникли в 70-80-х годах прошлого века. Они прочно вошли в обиход математиков и программистов. Слово "фрактал" происходит от латинского fractus, что в переводе означает разбитый (поделённый на части). Оно было предложено американским математиком Бенуа Мандельбротом в 1975 году для обозначения нерегулярных самоподобных структур. По определению, данному Мандельбротом, "фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому". Свойство самоподобности отражает главную особенность природных объектов, когда отдельная клетка растения или животного несёт в себе полную информацию обо всём организме.

Рождение фрактальной геометрии принято связывать с выходом в 1977 году книги Мандельброта "Фрактальная геометрия природы". В ней использованы научные результаты учёных, работавших в период 1875-1925 гг. в той же области. Среди них Пуанкаре, Фату, Жюлиа, Кантор, Хаусдорф. Только в наше время удалось объединить эти работы в единую систему.

С математической точки зрения фрактал - это прежде всего множество дробной размерности. Дробная размерность - основное свойство фракталов. В обычной геометрии линия имеет одно измерение, поверхность — два измерения, а пространственная фигура трехмерна. Фракталы же — это не линии и не поверхности, а, если можно это себе представить, нечто среднее. С ростом размеров возрастает и объем фрактала, но его размерность (показатель степени) — величина не целая, а дробная, а потому граница фрактальной фигуры не линия: при большом увеличении становится видно, что она размыта и состоит из спиралей и завитков, повторяющих в малом масштабе саму фигуру. Такая геометрическая регулярность называется масштабной инвариантностью или самоподобием. Она-то и определяет дробную размерность фрактальных фигур.

До появления фрактальной геометрии наука имела дело с системами, заключенными в трех пространственных измерениях. Благодаря Эйнштейну стало понятно, что трехмерное пространство — только модель действительности, а не сама действительность. Фактически наш мир расположен в четырехмерном пространственно-временном континууме.
      Благодаря Мандельброту стало понятно, как выглядит четырехмерное пространство, образно выражаясь, фрактальное лицо Хаоса. Бенуа Мандельброт обнаружил, что четвертое измерение включает в себя не только первые три измерения, но и (это очень важно!) интервалы между ними.

Фрактальная геометрия - это революция в математике и математическом описании природы. Вот как об этом пишет сам первооткрыватель фрактальной геометрии Бенуа Мандельброт: "Почему геометрию часто называют холодной и сухой? Одна из причин заключается в её неспособности описать форму облака, горы, дерева или моря. Облака - это не сферы, горы - это не конусы, линии берега - это не окружности, и кора не является гладкой, и молния не распространяется по прямой…

Новая фигура - фрактал - может выступать моделью сложных природных систем, таких, как кроны деревьев, горные хребты, береговые линии, поверхность Луны, и т.д. Древовидные фракталы применяются для моделирования не только растений, но и бронхиального дерева, работы почек, кровеносной системы.

1.2. Классификация фракталов

Геометрические фракталы

Этот тип фракталов получается путем простых геометрических построений. Обычно при построении этих фракталов поступают так: берется "затравка" - аксиома - набор отрезков, на основании которых будет строиться фрактал. Далее к этой "затравке" применяют набор правил, который преобразует ее в какую - либо геометрическую фигуру. Далее к каждой части этой фигуры применяют опять тот же набор правил. С каждым шагом фигура будет становиться все сложнее и сложнее, и если мы проведем бесконечное количество преобразований - получим геометрический фрактал.

Фракталы этого класса самые наглядные, потому что в них сразу видна самоподобность при любых масштабах наблюдения. Примерами таких фракталов служат: кривая Коха, кривая Пeано, кривая Минковского.

Кривая Коха является типичным геометрическим фракталом. Процесс её построения выглядит следующим образом: берём единичный отрезок, разделяем на три равные части и заменяем средний интервал равносторонним треугольником без этого сегмента. В результате образуется ломаная, состоящая из четырех звеньев длины 1/3. На следующем шаге повторяем операцию для каждого из четырёх получившихся звеньев и т. д… Предельная кривая и есть кривая Коха. Выполнив аналогичные преобразование на сторонах равностороннего треугольника можно получить фрактальное изображение снежинки Коха.

Также ещё одним несложным представителем геометрического фрактала является квадрат Серпинского. Строится он довольно таки просто: квадрат делится прямыми, параллельными его сторонам, на 9 равных квадратов. Из квадрата удаляется центральный квадрат. Получается множество, состоящее из 8 оставшихся квадратов "первого ранга". Поступая точно так же с каждым из квадратов первого ранга, получим множесто, состоящее из 64 квадратов второго ранга. Продолжая этот процесс бесконечно, получим бесконечную последовательность или квадрат Серпинского.

Алгебраические фракталы

Это самая крупная группа фракталов. Алгебраические фракталы получили свое название за то, что их строят, используя простые алгебраические формулы.

Получают их с помощью нелинейных процессов в n-мерных пространствах. Алгебраические фракталы строятся на основе алгебраических формул. Берется некая функция, в которую входит комплексное число, и начинают ее рассчитывать, пока не выполнится некоторое условие. И когда это условие выполнится на экран выводится точка, цвет которой зависит от номера итерации. Значение функции при этом может вести себя совершенно по разному: стремится к бесконечности, стремится к нулю, принимать фиксированное значение или вести себя хаотично.

Меняя алгоритм выбора цвета, можно получить сложные фрактальные картины с причудливыми многоцветными узорами. Неожиданностью для математиков стала возможность с помощью примитивных алгоритмов порождать очень сложные структуры.

В качестве примера рассмотрим множество Мандельброта. Строят его с помощью комплексных чисел.

Множеству Мандельброта принадлежат точки, которые в течение бесконечного числа итераций не уходят в бесконечность (точки, имеющие черный цвет). Точки, принадлежащие границе множества (именно там возникает сложные структуры) уходят в бесконечность за конечное число итераций, а точки, лежащие за пределами множества, уходят в бесконечность через несколько итераций (белый фон).

Пример другого алгебраического фрактала – множество Жюлиа. Существует 2 разновидности этого фрактала. Удивительно, но множества Жюлиа образуются по той же самой формуле, что и множество Мандельброта.

Стохастические фракталы

Еще одним известным классом фракталов являются стохастические фракталы, которые получаются в том случае, если в итерационном процессе случайным образом менять какие - либо его параметры. При этом получаются объекты очень похожие на природные - несимметричные деревья, изрезанные береговые линии и т.д.

Типичным представителем этой группы фракталов является «плазма». Для ее построения берется прямоугольник и для каждого его угла определяется цвет. Далее находится центральная точка прямоугольника и раскрашивается в цвет равный среднему арифметическому цветов по углам прямоугольника плюс некоторое случайное число. Чем больше случайное число - тем более "рваным" будет рисунок. Если же предположить, что цвет точки это высота над уровнем моря - получим вместо плазмы - горный массив. Именно на этом принципе моделируются горы в большинстве программ. С помощью алгоритма, похожего на плазму строится карта высот, к ней применяются различные фильтры, накладывается текстура и фотореалистичные горы готовы

Если посмотреть на этот фрактал в разрезе то мы увидим этот фрактал объемный, и имеет «шероховатость», как раз из-за этой «шероховатости» есть очень важное применение этого фрактала. Допустим нужно описать форму горы. При совмещении обычной геометрии с фрактальной можно получить ту самую «шероховатость» горы. На обычный конус нужно наложить плазму и мы получим рельеф горы.

1.3. Фрактальная геометрия природы

До появления неевклидовой геометрии Н.И. Лобачевского - Л. Больяи, существовала только одна геометрия - та, которая была изложена в "Началах", и вопрос о том, что такое геометрия и какая из геометрий является геометрией реального мира, не возникал, да и не мог возникнуть. Но с появлением еще одной геометрии возник вопрос, что такое геометрия вообще, и какая из множества геометрий отвечает реальному миру. Фрактальная геометрия занимается изучением инвариантов группы самоаффинных преобразований, т.е. свойств, выражаемых степенными законами.

Что же касается соответствия реальному миру, то фрактальная геометрия описывает весьма широкий класс природных процессов и явлений, и поэтому мы можем вслед за Б.Мандельбротом с полным правом говорить о фрактальной геометрии природы. Новые - фрактальные объекты обладают необычными свойствами. Длины, площади и объемы одних фракталов равны нулю, других - обращаются в бесконечность.

Природа зачастую создаёт удивительные и прекрасные фракталы, с идеальной геометрией и такой гармонией, что просто замираешь от восхищения.

Молнии восхищают своей красотой. Фракталы, созданные молнией не произвольны и не регулярны.

Фрактальная форма подвида цветной капусты (Brassica cauliflora). Это особый вид является особенно симметричным фракталом.

Папоротник так же является хорошим примером фрактала среди флоры.

Павлины всем известны своим красочным опереньем, в котором спрятаны сплошные фракталы.

Лёд, морозные узоры на окнах это тоже фракталы.

От увеличенного изображения листочка, до ветвей дерева - во всём можно обнаружить фракталы. Фракталы есть везде и всюду в окружающей нас природе. Вся Вселенная построена по удивительно гармоничным законам с математической точностью. Разве можно после этого думать, что наша планета это случайное сцепление частиц? Едва ли.

1.4. Применение фракталов

В наши дни теория фракталов находит широкое применение в различных областях человеческой деятельности.

Очень часто фракталы применяются в геологии и геофизике. Побережья островов и континентов имеют некоторую фрактальную размерность, зная которую можно очень точно вычислить длины побережий.

Исследование разломной тектоники и сейсмичности порой тоже исследуется с помощью фрактальных алгоритмов. Геофизика использует фракталы и фрактальный анализ для исследования аномалий магнитного поля, для изучения распространение волн и колебаний в упругих средах.

В физике фракталы применяются очень широко. В физике твёрдых тел фрактальные алгоритмы позволяют точно описывать и предсказывать свойства твёрдых, пористых, губчатых тел, аэрогелей. Это помогает в создании новых материалов с необычными и полезными свойствами. Пример твёрдого тела - кристаллы.

Изучение турбулентности в потоках очень хорошо подстраивается под фракталы.

В биологии они применяются для моделирования популяций и для описания систем внутренних органов (система кровеносных сосудов).

В данное время фракталы находят широкое применение в медицине. Сам по себе человеческий организм состоит из множества фрактальных структур: кровеносная система, мышцы, бронхи, бронхиальные пути в легких, артерии.

Теория фракталов применятся для анализа электрокардиограмм

Оценка величины и ритмов фрактальной размерности позволяют на более ранней стадии и с большей точностью и информативностью судить о нарушениях гомеостазиса и развитии конкретных заболеваний сердца.

Рентгеновские снимки, обработанные с помощью фрактальных алгоритмов, дают более качественную картинку, а соответственно и более качественную диагностику.

Еще одна область активного применения фракталов – гастроэнтерология. Новый метод исследования в медицине, электрогастроэнтерография — метод исследования, позволяющий оценить биоэлектрическую активность желудка, двенадцатиперстной кишки и других отделов ЖКТ.

Фрактальный принцип развития природных и геометрических объектов проникает вглубь архитектуры и как образ внешнего решения объекта, и как внутренний принцип архитектурного формообразования.

Дизайнеры со всего мира начали использовать в своих работах замечательные фрактальные структуры, только недавно описанные видными математиками. Использование фракталов поставило практически все направления современного дизайна на новый уровень. Привнесение фрактальных структур увеличило во многих случаях как визуальную, так и функциональную составляющие дизайна.

Также фрактальную геометрию используют для проектировании антенных устройств. Впервые это было применено американским инженером Натаном Коэном, который жил тогда в центре Бостона, где была запрещена установка на зданиях внешних антенн. Коэн вырезал из алюминиевой фольги фигуру в форме кривой Коха и затем наклеил ее на лист бумаги, а затем присоединил к приемнику. Оказалось, что такая антенна работает не хуже обычной. И хотя физические принципы такой антенны не изучены до сих пор, это не помешало Коэну обосновать собственную компанию и наладить их серийный выпуск. Так называемая фрактальная антенна располагается прямо на основной плате внутри аппарата.

Фракталы широко применяются в компьютерной графике для построения изображений природных объектов, таких как деревья, кусты, горные ландшафты, поверхности морей и так далее. Существует множество программ, служащих для генерации фрактальных изображений.

Чтобы получить трехмерную поверхность с использованием фрактального алгоритма, необходимо преобразовать множество Мандельброта в сферические координаты. Поскольку в природе мы часто наблюдаем фрактальные узоры, то искусственно созданный фрактальный трехмерный объект кажется невероятно реалистичным и даже «живым».

Фрактальный редактор позволяет создавать анимацию. Вы не только конфигурируете трехмерное множество Мандельброта, но и можете его вращать, масштабировать и менять параметры с течением времени.

Итак, можно с полной уверенностью сказать об огромном практическом применении фракталов и фрактальных алгоритмов на сегодняшний день.

Спектр областей, где применяются фракталы. очень обширен и разнообразен. И наверняка, в ближайшем будущем, фракталы, фрактальная геометрия, станут близки и понятны каждому из нас. Мы не сможем обходиться без них в нашей жизни!

Будем надеяться, что появление фрактальной геометрии есть свидетельство продолжающейся эволюции человека и расширения его способов познания и осознания мира. Возможно, наши дети будут также легко и осмысленно оперировать понятиями фракталов и нелинейной динамики, как мы оперируем понятиями классической физики, эвклидовой геометрии.

2. Практическая глава «Обзор программного обеспечения генерации фракталов»

2.1. Моделирование фракталов на языке Pascal ABC

PascalABC.NET — это язык программирования Паскаль нового поколения, который включает в себя классический Паскаль, большинство возможностей языка Delphi, а также ряд собственных расширений.

PascalABC.NET является мультипарадигменным языком: на нем можно программировать в структурном, объектно-ориентированном и функциональном стилях. Также это простая и мощная интегрированная среда разработки, поддерживающая технологию IntelliSense, содержащая средства автоформатирования, встроенный отладчик и встроенный дизайнер форм.

Среда PascalABC.NET проектируется как простая, но мощная оболочка, обеспечивающая подсветку синтаксиса, подсказку по коду (подсказка по точке, подсказка параметров подпрограмм, всплывающая подсказка по именам), форматирование текста программы по запросу, переход к определению и реализации подпрограммы, элементы рефакторинга. Она разрабатывается в большей степени с целью обучения программированию и содержит в своем составе ряд дополнительных модулей, предназначенных для обучения.

Особенности:

• доступ к существующим .NET библиотекам и возможность создания новых. В частности, существуют библиотеки для основных алгоритмов и структур данных.

• среда разработки, ориентированная на обучение: подсказки по коду, отладчик, автоформатирование кода и подсветка синтаксиса, простая навигация по коду и т.д.

• поддержка современных возможностей языков программирования: модули, классы, пространства имен, обработка исключений, сборка мусора и т.д.

• средства параллельного программирования (директивы OpenMP).

• обучающий инструментарий, сохранившийся с Pascal ABC: встроенный задачник, механизм проверяемых заданий, "исполнители" Робот и Чертежник и т.д.

По функциональному назначению выделяется три области экрана:

• строка меню;

• рабочая область;

• строка состояния.

В рабочей области есть возможность открывать различные окна программы: окна редактируемого текста, окна помощи, отладки и настройки. Имя файла написано в заголовке окна. Строка состояния показывает некоторые доступные и важные в настоящее время операции и комбинации клавиш соответствующие им.

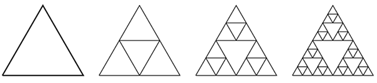
Рассмотрим пример создания геометрического фрактала - треугольника Серпинского. Чтобы его получить, нужно взять (равносторонний) треугольник с внутренностью, провести в нём средние линии и выкинуть центральный из четырех образовавшихся маленьких треугольников. Дальше эти же действия нужно повторить с каждым из оставшихся трех треугольников, и т. д. На рисунке показаны первые три шага.

Выкидывание центральных треугольников — не единственный способ получить в итоге треугольник Серпинского. Можно двигаться "в обратном направлении": взять изначально "пустой" треугольник, затем достроить в нём треугольник, образованный средними линиями, затем в каждом из трех угловых треугольников сделать то же самое, и т. д. Поначалу фигуры будут сильно отличаться, но с ростом номера итерации они будут всё больше походить друг на друга, а в пределе совпадут.

Вот наш конечный код написание нашей программы треугольника Серпинского в среде программирования PascalABC.NET.

program Serpinskiy;

uses CRT, GraphABC;

var

gd, gm : Integer;

const

iter = 9;

procedure tr(x1, y1, x2, y2, x3, y3: Real);

begin

Line(Round(x1), Round(y1), Round(x2), Round(y2));

Line(Round(x2), Round(y2), Round(x3), Round(y3));

Line(Round(x3), Round(y3), Round(x1), Round(y1));

end;

procedure draw(x1, y1, x2, y2, x3, y3: Real; n: Integer);

var

x1n, y1n, x2n, y2n, x3n, y3n : Real;

begin

if n 0 then

begin

x1n := (x1 + x2) / 2;

y1n := (y1 + y2) / 2;

x2n := (x2 + x3) / 2;

y2n := (y2 + y3) / 2;

x3n := (x3 + x1) / 2;

y3n := (y3 + y1) / 2;

tr(x1n, y1n, x2n, y2n, x3n, y3n);

draw(x1, y1, x1n, y1n, x3n, y3n, n - 1);

draw(x2, y2, x1n, y1n, x2n, y2n, n - 1);

draw(x3, y3, x2n, y2n, x3n, y3n, n - 1);

end;

end;

begin

tr(320,10,600,470,40,470);

draw(320,10,600,470,40,470,iter);{}

end.

Готовая программа в PascalABC.NET.

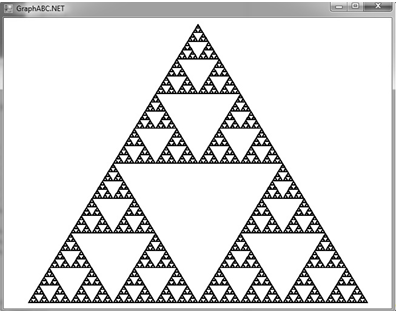
После того как написали код, следует запустить нашу программу. Для этого заходим в раздел "Программа" и выбираем пункт "Выполнить без связи с оболочкой".

После запуска откроется дополнительное окно, в котором мы можем увидеть наш готовый рисунок.

2.2. Построение фрактала в программе Fractal Explorer

Fractal Explorer – ведущее приложение для создания, просмотра и редактирования фрактальной графики. Программа работает со всеми популярными расширениями и позволяет конвертировать файлы в форматы типа fr.

Достоинства фрактал эксплорер: инновационный движок, обеспечивающий высокую скорость рендера и неограниченное уменьшение и приближения картинки. В текущей версии присутствует множество новых фильтров и готовых узоров, браузер файлов и меню предпросмотра. Утилита позволяет сразу выводить изображения на печать, экономя время пользователей.

Интерфейс Fractal Explorer достаточно прост, представлен в виде стандартных фоторедакторов. Включает в себя рабочее поле, панель инструментов и список с расширенными настройками.

Fractal Explorer может создавать классические полиномиальные фрактальные множества (например, следующие наборы -Mandelbrot-set, the Julia-set, the Newton-set и их вариаций), набор из 22 квартерионов (4D комплексные фракталы), 3D attractors, и IFS. Кроме того, FE имеет множество функций для создания спецэффектов и улучшения изображений — в постобработке полученных фракталов. И ещё интересную, но сейчас уже малоэффективную функцию - возможность создания Landscapes (земных поверхностей). 

Рассмотрим пример создания фрактала «Радужный цветок».

Открыли 2D фрактал  , заходим в окно с формулами  . Вот что вы видите сначала. По умолчанию открывается формула Classic Mandelbrot.

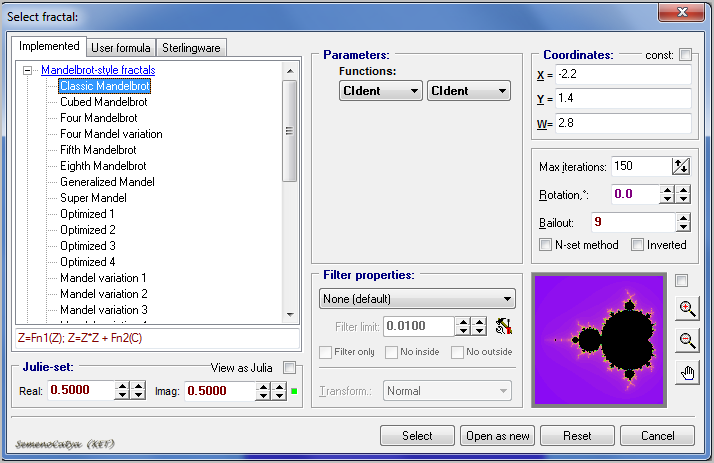
Но нам совсем не обязательно работать с этой формулой. Какую выбрать формулу - это ваше личное дело. Выбираем формулу. Я  перешла во вкладку Sterlingvare и выбрала формулу 06. На превью вы можете видеть как изменился наш фрактал.

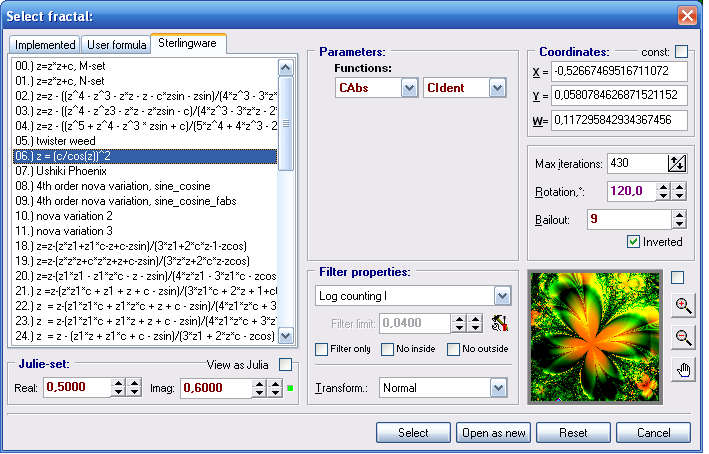
Выбираем операцию Select и закрываем это окно и переходим в окно градиентов  .. Здесь же выставлять значения цветовой палитры.

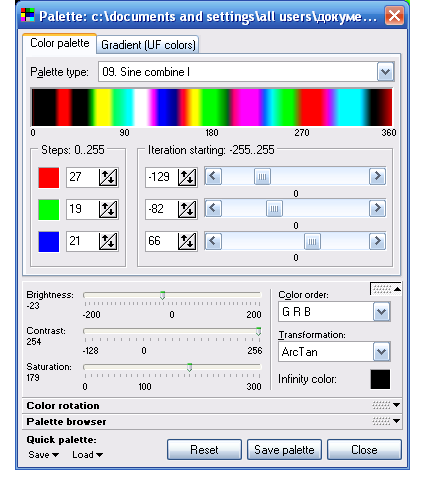
Установить размер и сохраняем. Размер можно поменять нажав на эту кнопку

Теперь сохраняем: 1. сохранить картинку (выбираете любой удобный для вас формат); 

2. Сохранить спот (т.е. рабочий вариант, который можно будет править) 

Пример готового изображения

Если вы не хотите потерять достигнутый результат, а поработать с этим фракталом вам ещё хочется, нажмите на вашей клавиатуре сочетание клавиш Ctrl+D. У вас откроется дубликат вашего фрактала. Вот с ним мы можем продолжить работу.

2.3. Построение фрактала в программе Incendia

Поддерживает 2X сглаживание, предустановленные 45 типов фракталов 3D, поддерживает скрипты, имеется библиотека текстур, так же возможен импорт внешних созданных в формате bmp, удобная работа с градиентом, несколько стилей рендера (включая объёмный туман и многие новые шейдеры визуализации), генератор хорошо работает с многоядерными процессорами, наличие 3D Baseshapes - форм (включает в себя шесть различных baseshapes карт смещения) расширяет творческие возможности при создании фракталов, присутствует редактор Tranformation а так же редактор самих форм baseshape, редактор материалов, возможен экспорт сетки 3D Mesh Export, сохранение данных в буфер, кроме того программа позволяет создавать анимацию.

Рассмотрим пример создания фрактала «Черный жемчуг».

Открываем Incendia. По умолчанию создается фрактальный треугольник с тремя трансформациями.

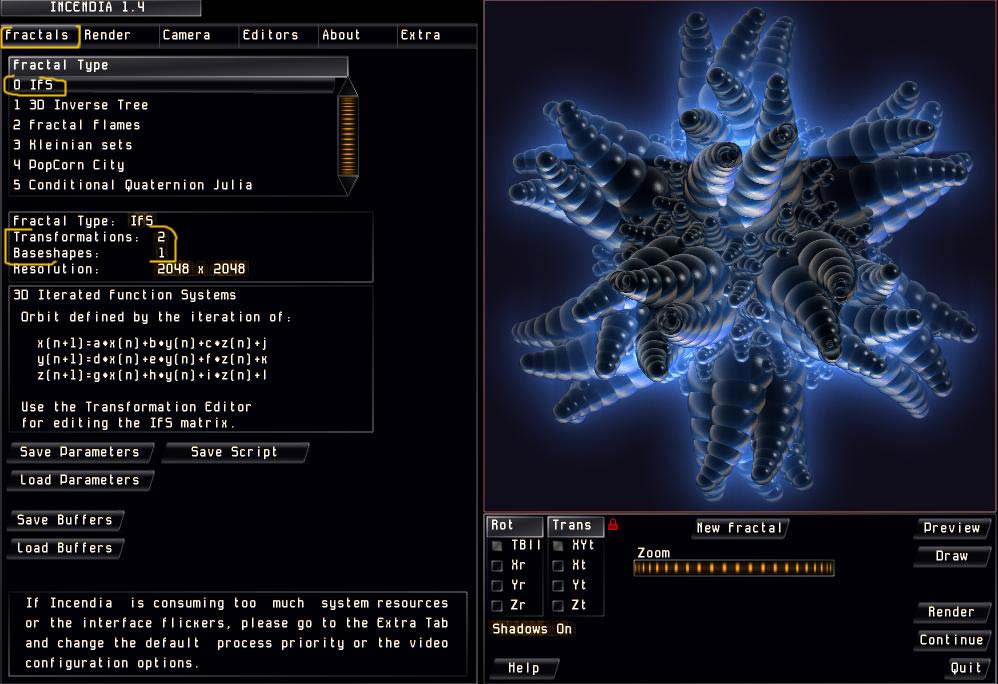
Выбираем вкладку Baseshapes, включеам кнопку Edite, нажимаем на кнопку New (добавляем в наш фрактал форму 0), в открывшейся библиотеке форм выбираем шар и вводим нужные параметры.

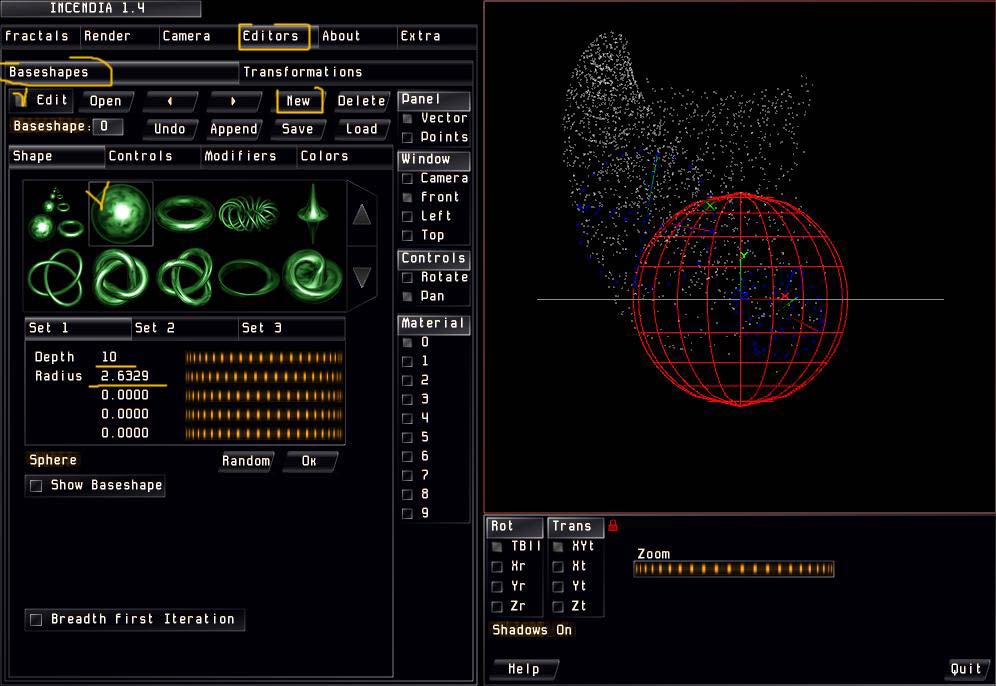
На вкладке Transformations удаляем третью (по умолчанию) форму, а с оставшимися двумя работаем: располагаем их нужным образом в пространстве.

Ф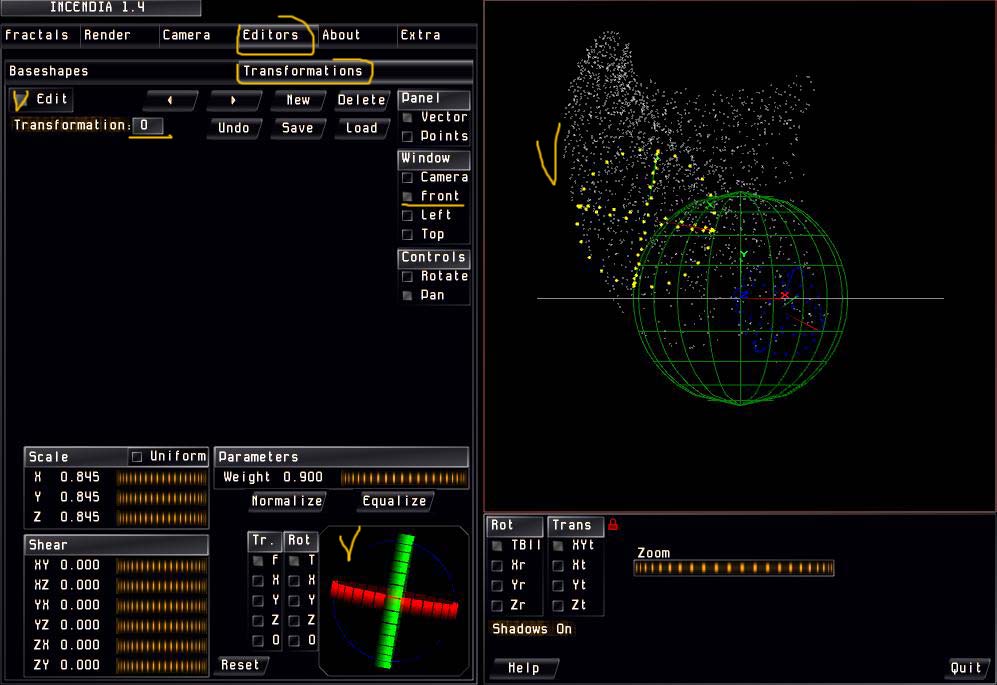 орма 0.

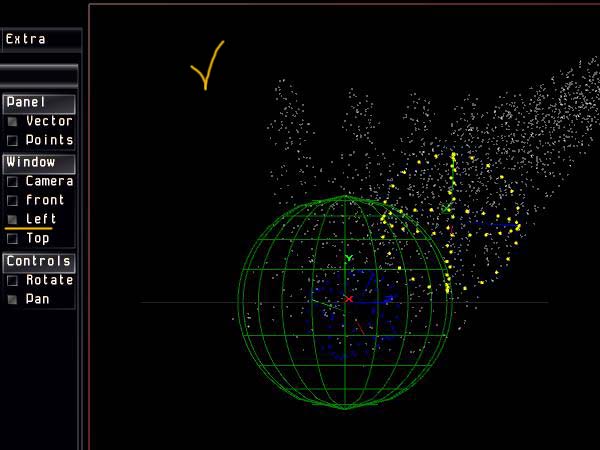
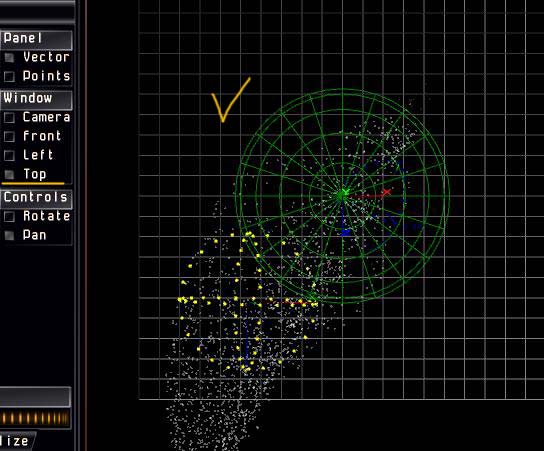
Форма 1.

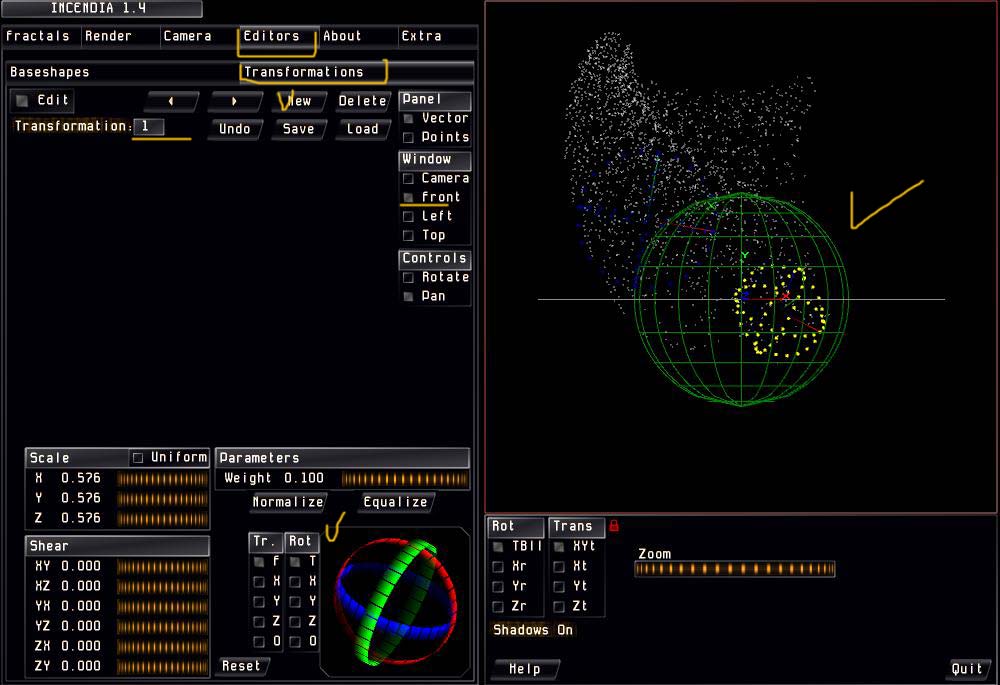
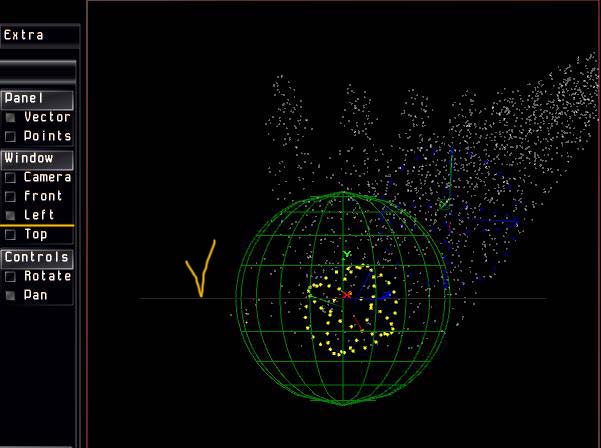
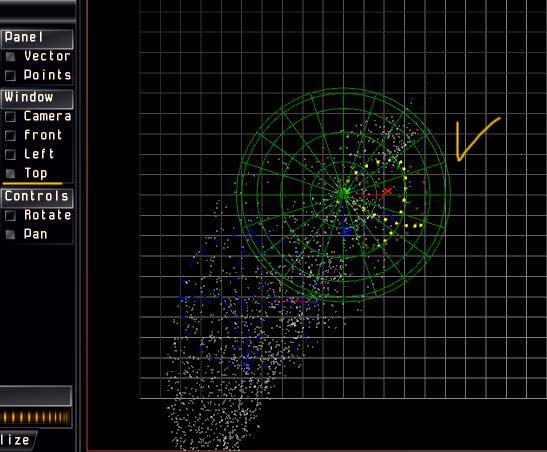
На вкладке Camera выставляем свет, включаем тени, а также отмечаем симметричность расположения фрактала.

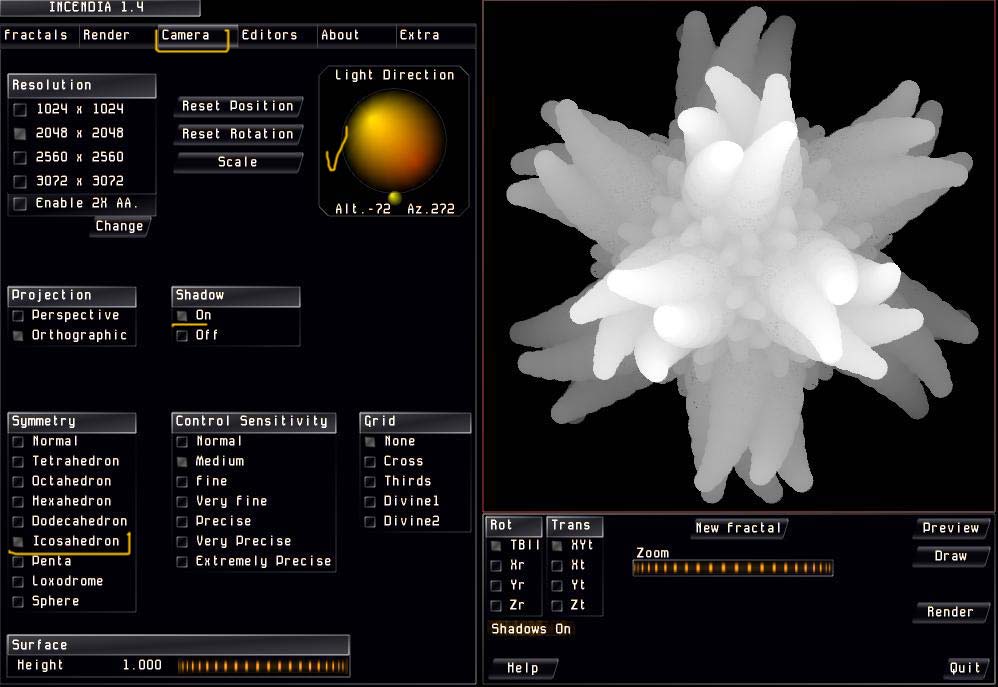
Переходим во вкладку Render подвкладку Materials, присваиваем текстуры и выставляем параметры.

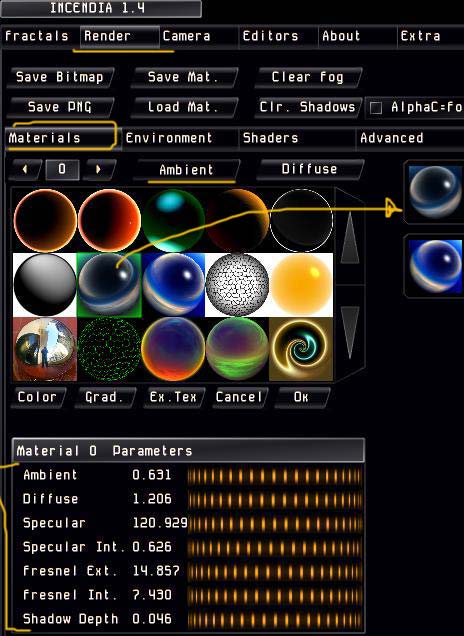
На подвкладке окружающей среды Environment меняем цвет фона, прибавляем синего свечения вокруг объекта о потом при рендеринге более детально работаем с данными параметрами.

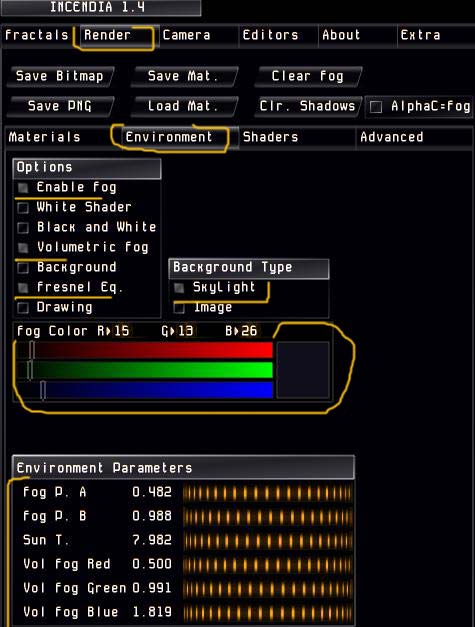
Заглянем в просмотровое окно, нажав кнопку Preview (предпросмотр) предварительно выключив обе кнопки Edite на вкладке Editors и если вас все устраивает, нажимаем кнопку Render. Даем изображению просчитаться несколько минут, после чего его можно сохранять, нажав кнопку Save Bitmap или Save Png на вкладке Render, если результат не устраивает продолжаем рендерить изображение дальше, нажав на появившуюся кнопку Continue без потери отсчитанного результата.

Заключение

Данная работа является введением в мир фракталов. Мы рассмотрели только самую малую часть того, какие бывают фракталы, на основе каких принципов они строятся.

Фрактальная графика - это не просто множество самоповторяющихся изображений, это модель структуры и принципа любого сущего. Вся наша жизнь представлена фракталами. Вся окружающая нас природа состоит из них. Нельзя не отметить широкое применение фракталов в компьютерных играх, где рельефы местности зачастую являются фрактальными изображениями на основе трёхмерных моделей комплексных множеств. Фракталы очень сильно облегчают рисование компьютерной графики, с помощью фракталов создаются множество спецэффектов, различных сказочных и невероятных картинок и т.д. Также с помощью фрактальной геометрии рисуются деревья, облака, берега и вся другая природа. Фрактальная графика необходима везде, и развитие "фрактальных технологий" - это одна из немаловажных задач на сегодняшний день.

Роль фракталов в машинной графике сегодня достаточно велика, и я убедился в этом, выполняя исследовательскую работу, в ходе которой научился строить некоторые виды фракталов, узнал, что существуют специальные программы для моделирования фракталов, убедился в том, что область применения фракталов чрезвычайно велика. Фактически найден способ легкого представления сложных неевклидовых объектов, образы которых весьма похожи на природные.

Компьютеры становятся все мощнее, и все более тонкие эффекты они позволяют нам наблюдать на экране дисплея. Нас ждет еще много интереснейших и необычайных находок.

Данную работу можно использовать на уроках информатики при изучении графики в среде PascalABC, а так же на уроках геометрии и искусства.

Составленные мною программы, служат положительным мотивом для учащихся, начинающих изучать языки программирования. Ведь когда из непонятных букв и цифр рождается фрактал. Это вызывает живой интерес попробовать самому.

Нами также разработан буклет, который знакомит с понятием и видами фрактала.

Цели, поставленные в начале работы были достигнуты. Но останавливаться на достигнутом мы не собираемся. Мне хотелось бы в дальнейшем продолжить изучение специализированных программ для создания фракталов.

Список использованных источников

1. Божокин С.В., Паршин Д.А. Фракталы и мультифракталы. РХД, 2001.

2. Витолин Д. Применение фракталов в машинной графике // Computerworld- Россия -1995.

3. Мандельброт Б. Самоаффинные фрактальные множества, «Фракталы в физике». М.: Мир 1988 г.

4. Мандельброт Б. Фрактальная геометрия природы. — М.: «Институт компьютерных исследований», 2002.

5. Морозов А.Д. Введение в теорию фракталов. Н.Новгород: Изд-во Нижегород. ун-та 1999 г.

6. Пайтген Х.-О., Рихтер П. Х. Красота фракталов. — М.: «Мир», 1993.

Интернет ресурсы

1. http://www.ghcube.com/fractals/determin.html

2. http://arbuz.uz/s_fractal.html

3. http://fractals.nsu.ru/fractals.chat.ru/

4. http://fractals.nsu.ru/animations.htm

5. http://www.cootey.com/fractals/index.html

6. http://fraktals.ucoz.ru/publ

7. http://ega-math.narod.ru/Nquant/Fractals.htm

8. http://sakva.narod.ru

9. http://rusnauka.narod.ru/lib/author/kosinov_n/12/

10. http://www.cnam.fr/fractals/

11. http://www.softlab.ntua.gr/mandel/

12. http://www.math.yale.edu/mandelbrot/

13. http://fractalworld.xaoc.ru/

14. http://fractbifur.narod.ru/html/index1.html

15. http://subscribe.ru/archive/job.education.maths/201005/06210524.htm