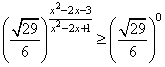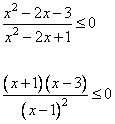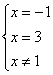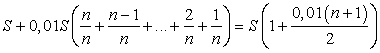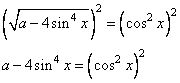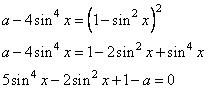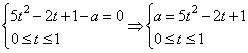Вариант 2. ЕГЭ 2021 11 класс Решение.

Вариант 2. ЕГЭ 2021 11 класс Решение.

Задание 1. Для покраски потолка требуется 200 г краски на 1 м2. Краска продаётся в банках по 2 кг. Сколько банок краски нужно купить для покраски потолка площадью 64 м2?

Решение.

Для 64 кв м потолка требуется

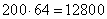 г.

Краска продается по 2 кг в банке (т.е. по 2000 г), значит, банок потребуется

,

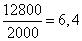т.е. 7 полных банок.

Ответ: 7.

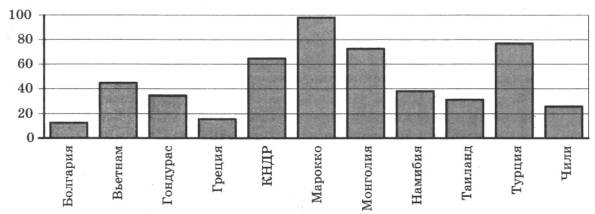
Задание 2. На диаграмме показано распределение выплавки цинка в 11 странах мира (в тысячах тонн) за 2009 год. Среди представленных стран первое место по выплавке цинка занимало Марокко, одиннадцатое место — Болгария. Какое место занимал Таиланд?

Решение.

Из условия задачи видно, что чем выше столбец, тем выше место в рейтинге соответствующей страны. С учетом этого получаем, что Таиланд занимает 8-е место.

Ответ: 8.

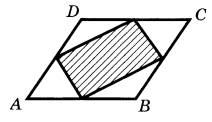
Задание 3. Площадь параллелограмма ABCD равна 170. Найдите площадь четырёхугольника, вершинами которого являются середины сторон данного параллелограмма.

Решение.

Из рисунка можно заметить, что противолежащие по диагонали треугольники равны по площади. Если составить эти треугольники вместе, то они займут площадь в точности равную половине площади параллелограмма (учитывая, что вершины четырехугольника находятся в середине сторон параллелограмма). Таким образом, площадь закрашенной фигуры будет равна

170:2=85.

Ответ: 85.

Задание 4.Вариант 1. ЕГЭ 50 вариантов

 Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная батарейка будет забракована системой контроля.

Решение.

Выделим два несовместных исхода, при которых система контроля бракует батарейку:

- батарейка неисправна и она бракуется системой;

- батарейка исправна и она бракуется системой.

Вероятность первого исхода равна 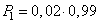 , вероятность второго исхода равна  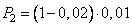. В результате, искомая вероятность, равна:

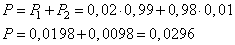
Ответ: 0,0296.

Задание 5. Найдите корень уравнения  .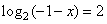

Решение.

Избавимся от знака логарифма, получим:

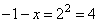
и вычислим корень уравнения

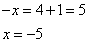
Ответ: -5.

Задание 6. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Найдите высоту трапеции.

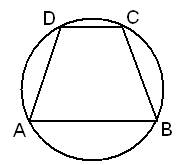
Решение.

Сделаем построение, проведем высоту KH через центр окружности O (см. рисунок ниже).

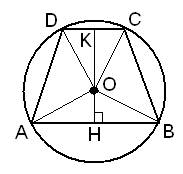
Из рисунка видно, что треугольники DOC и AOB – равнобедренные и их высоты KO и HO делят стороны DC и AB пополам. Найдем эти высоты из прямоугольных треугольников DKO и AOH по теореме Пифагора, имеем:

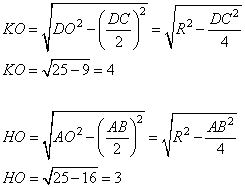
Следовательно, высота трапеции, равна

KH=KO+HO=4+3=7.

Ответ: 7.

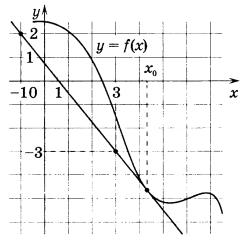
Задание 7. На рисунке изображены график функции у = f(x) и касательная к нему в точке с абсциссой 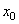 . Найдите значение производной функции f(x) в точке  .

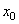Решение.

Значение производной в точке 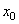  равно тангенсу угла наклона касательной к оси OX в точке  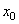. Для вычисления тангенса, выполним построение, показанное на рисунке ниже.

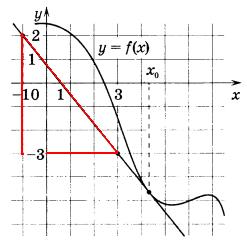
Из прямоугольного треугольника находим, что тангенс (и что то же самое производная) равен

.

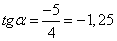Ответ: -1,25.

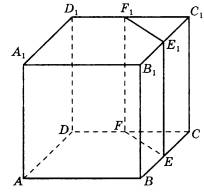
Задание 8. В кубе ABCDA1B1C1D1 точки Е, F, Е1 и F1 являются серединами рёбер ВС, DC, В1С1 и D1C1 соответственно. Объём призмы, отсекаемой от куба плоскостью EFF1 равен 9. Найдите объём куба.

Решение.

Посмотрим сверху на верхнюю грань куба. Это будет квадрат. Отрезок 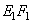  образует вместе с вершиной  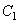 треугольник. На рисунке ниже показано, что таких треугольников размещается ровно 8 и они полностью покрывают поверхность квадрата.

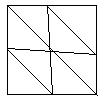
Отсюда следует, что объем куба в 8 раз больше объема призмы и равен

.

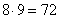Ответ: 72

Задание 9. Найдите sina, если 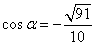  и  .

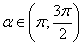Решение.

Выразим функцию синуса через функцию косинуса, получим:

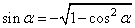
и подставим вместо  :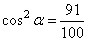

.

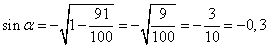Ответ: -0,3.

Задание 10. Для обогрева помещения, температура в котором равна 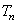  = 25 °С, через радиатор отопления, пропускают горячую воду температурой  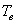 = 65 °С. Расход проходящей через трубу воды m = 0,3 кг/с. Проходя по трубе расстояние  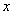 (м), вода охлаждается до температуры Т (°С), причём  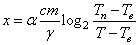 (м), где c = 4200  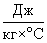 — теплоёмкость воды,  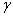 = 42 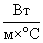  — коэффициент теплообмена, а  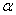 = 1,3 — постоянная. До какой температуры (в градусах Цельсия) охладится вода, если длина трубы 117 м?

Решение.

Найдем температуру 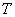  воды, которая прошла по трубе длиной  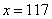 метров, получим:

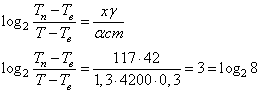
Перейдем к подлогарифмическим выражениям, имеем:

,

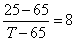откуда

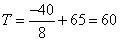 градусов.

Ответ: 60.

Задание 11. На изготовление 416 детали первый рабочий тратит на 10 часов меньше, чем второй рабочий на изготовление 546 таких же деталей. Известно, что первый рабочий за час делает на 5 деталей больше, чем второй. Сколько деталей в час делает первый рабочий?

Решение.

Пусть 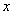  деталей делает первый рабочий за 1 час. По условию задачи, второй рабочий делает на 5 деталей меньше первого, т.е.  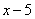 деталей. На изготовление 416 деталей первый рабочий тратит  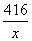 часов, а второй на изготовление 546 деталей  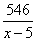 часов. Так как первый рабочий на изготовление 416 деталей тратит на 10 часов меньше, чем второй рабочий на изготовление 546 таких же деталей, получаем уравнение:

,

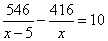преобразовываем к квадратному уравнению, имеем:

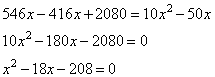
Решаем уравнение, получаем два корня:

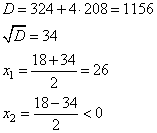
Таким образом, первый рабочий делает 26 деталей в час.

Ответ: 26.

Задание 12. Найдите точку максимума функции y=10+6x-2x√x.

Решение.

Найдем точки экстремума функции. Перепишем функцию в виде

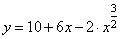
вычислим производную и приравняем ее нулю, получим:

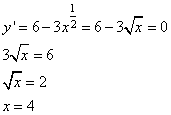
Нашли одну точку экстремума функции, которая и будет точкой максимума функции.

Ответ: 4.

Задание 13. а) Решите уравнение  .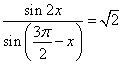

б) Найдите все корни этого уравнения, принадлежащие отрезку  .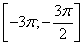

Решение.

а) Перепишем уравнение в виде

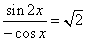
и положим 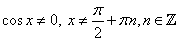 , и умножая уравнение на  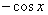, получим:

Так как 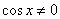 , то имеем одно уравнение

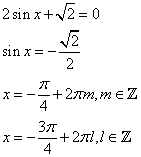
б) Найдем такие целые 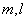 , при которых найденные корни попадают в интервал  :

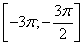- для 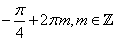 , имеем:

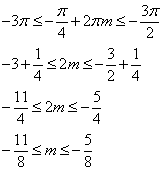
подходит целое значение 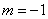  и корень  ;

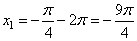- для 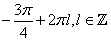 , имеем:

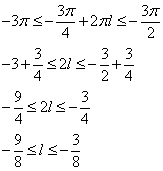
подходит целое 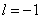  и корень  .

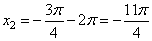Ответ: а) 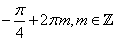 ;  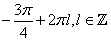; б)  .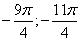

Задание 14. В правильной треугольной призме ABCA1B1C1 стороны основания равны 3, боковые ребра равны 1, точка D – середина ребра CC1.

а) Постройте прямую пересечения плоскостей ABC и ADB1.

б) Найдите угол между плоскостями ABC и ADB1.

Решение.

а) Построение. Плоскости ABC и 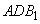  будут иметь две общие точки: точка  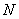, лежащая на пересечении отрезков BC и  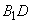 и точка A, находящаяся в основании призмы (см. рисунок). Отрезок AN, соединяющий эти две точки, будет образовывать прямую пересечения плоскостей ABC и  .

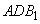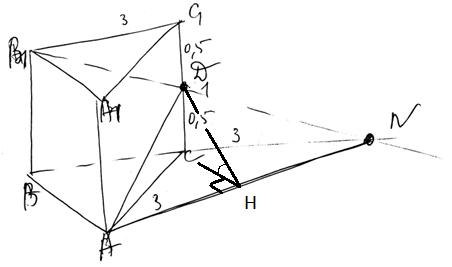
б) Угол между плоскостями будет соответствовать углу 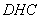 , причем отрезок  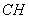 будет являться высотой треугольника ACN. Из рисунка видно, что треугольник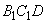и   и 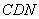  подобны друг другу с коэффициентом подобия  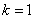. Отсюда следует, что отрезок  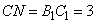. Сторона  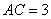. Следовательно, треугольник ACN равнобедренный с углом  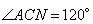 (так как угол  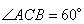 в силу того, что треугольник ABC равносторонний). В равнобедренном треугольнике высота CH будет являться также и биссектрисой. Высоту CH вычислим из прямоугольного треугольника CHN, в котором CN – гипотенуза с прилежащим к ней углом  :

.

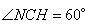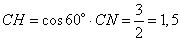Учитывая, что точка D лежит точно посередине отрезка 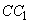 , получаем длину отрезка  .

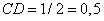Найдем тангенс угла 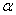  между плоскостями ABC и  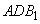 из прямоугольного треугольника CDH, получим:

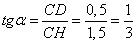
И .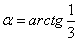

Ответ: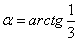

Задание 15. Решите неравенство  .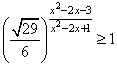

Решение.

Упростим неравенство, преобразуем его к следующему виду:

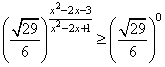
и так как 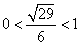  (то есть положительно и меньше 1), то переходя к степеням, меняем знак на противоположный, имеем:

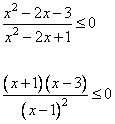
Из последнего неравенства имеем следующие точки, делящие числовую ось:

.

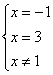
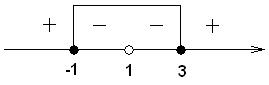
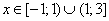Ответ:  .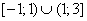

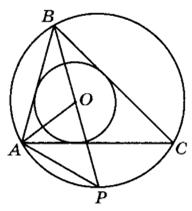
Задание 16. Точка О — центр вписанной в треугольник ABC окружности. Прямая ВО вторично пересекает описанную около этого треугольника окружность в точке Р.

а) Докажите, что углы POA = PAO.

б) Найдите площадь треугольника АРО, если радиус описанной около треугольника ABC окружности равен 6, углы BAC = 75°, ABC = 60°.

Решение.

а) Поскольку точка О — центр вписанной в треугольник ABC окружности, лучи АО и ВО являются биссектрисами углов треугольника ABC. Угол РОА является внешним углом треугольника АОВ. Следовательно,

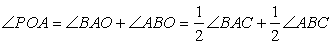
Углы РАС и РВС равны, поскольку опираются на одну и ту же дугу окружности, описанной около треугольника ABC, поэтому

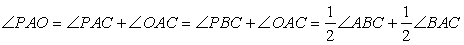
Таким образом,  .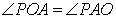

б) Пусть R = 6 — радиус окружности, описанной около треугольника ABC.

Поскольку 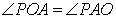 , треугольник АРО равнобедренный, следовательно,

.

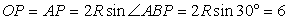Таким образом, площадь треугольника АРО равна

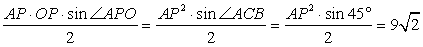
Ответ: 9√2.

Задание 17. 15-го января планируется взять кредит в банке на некоторый срок (целое число месяцев). Условия его возврата таковы:

- 1-го числа каждого месяца долг возрастает на 1 % по сравнению с концом предыдущего месяца;

- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

- 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.

На сколько месяцев планируется взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 20 % больше суммы, взятой в кредит? (Считайте, что округления при вычислении платежей не производятся.)

Решение.

Пусть сумма кредита равна S, а кредит планируется взять на n месяцев. По условию, долг перед банком по состоянию на 15-е число должен уменьшаться до нуля равномерно:

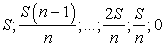
Первого числа каждого месяца долг возрастает на 1%, значит, последовательность размеров долга на 1-е число каждого месяца такова:

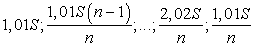
Следовательно, выплаты должны быть следующими:

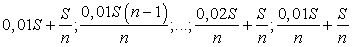
Всего следует выплатить

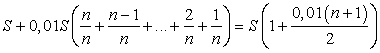
Общая сумма выплат на 20 % больше суммы, взятой в кредит, поэтому

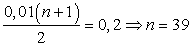
Ответ: 39.

Задание 18. Найдите все a, при каждом из которых уравнение 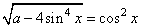  имеет решение.

Решение.

Возведем уравнение в квадрат, получим:

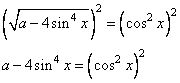
Обратите внимание, что при возведении в квадрат квадратного корня подкоренное выражение записано без модуля. Это связано с тем, что квадрат корня по условию должен быть равен  , который всегда больше 0. Далее преобразуем полученное уравнение:

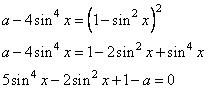
Введем обозначение 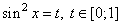 . В результате приходим к следующей системе:

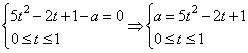
Решим данную систему в координатах 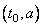 . Построим график функции  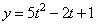 на отрезке [0;1] (см. рисунок ниже).

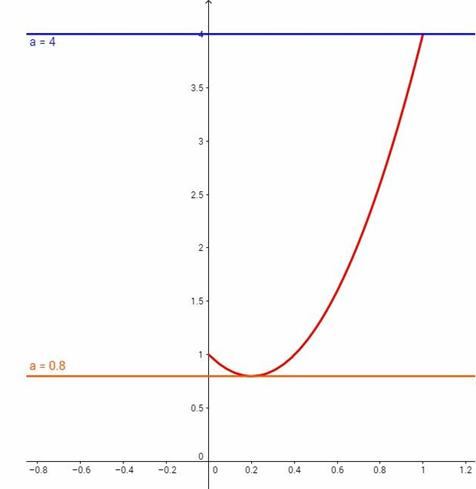
Система имеет решение при 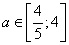  (см. горизонтальные линии на рисунке).

Ответ:  .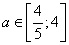

Задание 19. Имеется 8 карточек. На них записывают по одному каждое из чисел 101, -102, -103, 104, 105, -107, -108, 109. Карточки переворачивают и перемешивают. На их чистых сторонах заново пишут по одному каждое из чисел 101, -102, -103, 104, 105, -107, -108, 109. После этого числа на каждой карточке складывают, а полученные восемь сумм перемножают.

а) Может ли в результате получиться 0?

б) Может ли в результате получиться 21?

в) Какое наименьшее целое неотрицательное число может в результате получиться?

Решение.

а) Чтобы получить в результате произведения число 0 один из сомножителей должен быть равен 0. Однако никакая комбинация чисел представленной последовательности в сумме не дает 0, следовательно, такое число получиться не может.

б) Число 21 можно разложить на простые множители следующим образом:

.

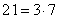Таким образом, чтобы получить число 21 должны быть множители 3 и 7, а остальные множители должны быть 1. Как видим из приведенных чисел, получить такую комбинацию невозможно.

в) Для получения наименьшего целого неотрицательного, нужно подобрать числа так, чтобы они в сумме давали минимальные значения (минимальные множители). Разобьем числа на пары одинаковых чисел следующим образом:

(101-102)=1 и (-102+101)=1

(-103+104)=1 и (104-103)=1

(105-107)=2 и (-107+105)=2

(-108+109)=1 и (109-108)=1

Произведение полученных чисел дает минимальное целое положительное 4.

Ответ: а) нет; б) нет; в) 4.
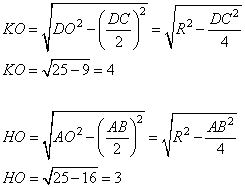
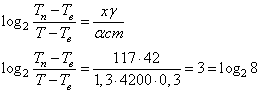
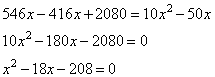
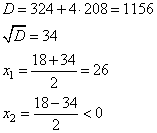
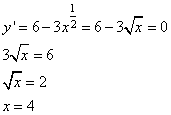
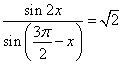
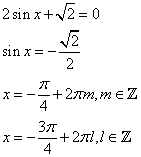
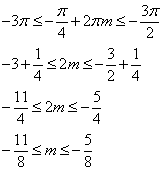
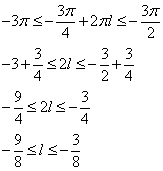
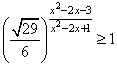