При выполнении заданий 2, 3, 8, 14 выберите один из четырёх предлагаемых вариантов ответа. Ответом на задания 1, 4—7, 9—13, 15—20 является целое число или конечная десятичная дробь. Дробную часть от целой отделяйте запятой. Единицы измерений писать не нужно.
Вариант № 2
1. Найдите значение выражения: 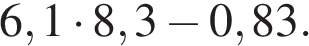
2. На координатной прямой отмечены числа a, b и c.

Какая из разностей a − b, a − c, c − b положительна?
В ответе укажите номер правильного варианта.
1) a − b
2) a − c
3) c − b
4) ни одна из них
3. Сравните числа  и 16.
и 16.
В ответе укажите номер правильного варианта.
1) 
2) 
3) 
4. Решите уравнение 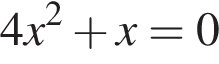 .
.
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
5. Найдите значение 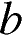 по графику функции
по графику функции 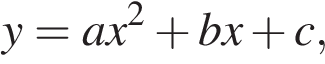 изображенному на рисунке.
изображенному на рисунке.
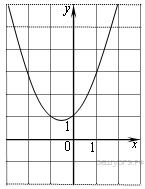
6. Дана арифметическая прогрессия (an), разность которой равна −2,5, a1 = −9,1. Найдите сумму первых 15 её членов.
7. Упростите выражение 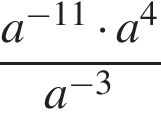 и найдите его значение при
и найдите его значение при 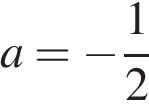 . В ответе запишите полученное число.
. В ответе запишите полученное число.
8. Укажите неравенство, решением которого является любое число.
В ответе укажите номер правильного варианта.
1) x2 − 15
2) x2 + 15 0
3) x2 + 15
4) x2 − 15 0
9. 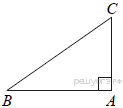 В треугольнике ABC угол A равен 90°, AC = 6, sin B = 0,3. Найдите BC.
В треугольнике ABC угол A равен 90°, AC = 6, sin B = 0,3. Найдите BC.
10. 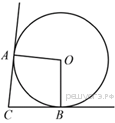 В угол C величиной 79° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.
В угол C величиной 79° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.
11. 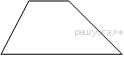 Основания трапеции равны 1 и 13, одна из боковых сторон равна
Основания трапеции равны 1 и 13, одна из боковых сторон равна  , а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
, а угол между ней и одним из оснований равен 135°. Найдите площадь трапеции.
12. 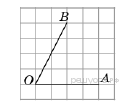 Найдите тангенс угла AOB, изображенного на рисунке.
Найдите тангенс угла AOB, изображенного на рисунке.
13. Укажите номера верных утверждений.
1) Центры вписанной и описанной окружностей равностороннего треугольника совпадают.
2) Существует квадрат, который не является ромбом.
3) Сумма углов любого треугольника равна 180° .
Если утверждений несколько, запишите их номера в порядке возрастания.
14. Бизнесмен Соловьёв выезжает из Москвы в Санкт-Петербург на деловую встречу, которая назначена на 10:00. В таблице дано расписание ночных поездов Москва — Санкт-Петербург.
| Номер поезда | Отправление из Москвы | Прибытие в Санкт-Петербург |
| 038А | 00:43 | 08:45 |
| 020У | 00:54 | 09:00 |
| 016А | 01:00 | 08:38 |
| 030А | 01:10 | 09:37 |
Путь от вокзала до места встречи занимает полчаса. Укажите номер самого позднего (по времени отправления) из московских поездов, которые подходят бизнесмену Соловьёву.
В ответе укажите номер правильного варианта.
1) 038А
2) 020У
3) 016А
4) 030А
15. На графике показано, сколько человек зарегистрировалось с 25 декабря 2012 года по 13 февраля 2013 года в качестве участников конференции. По горизонтали указаны числа месяцев, а по вертикали — количество человек.
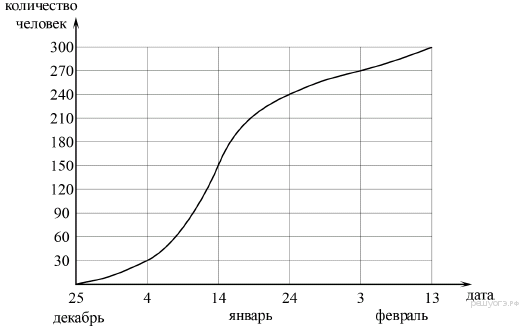
Во сколько раз возросло количество зарегистрировавшихся с 4 января по 3 февраля?
16. Магазин делает пенсионерам скидку на определённое количество процентов от стоимости покупки. Пакет сока стоит в магазине 75 рублей, а пенсионер заплатил за него 61 рубль 50 копеек. Сколько процентов составляет скидка для пенсионера?
17. Площадь прямоугольного земельного участка равна 9 га, ширина участка равна 150 м. Найдите длину этого участка в метрах.
18. 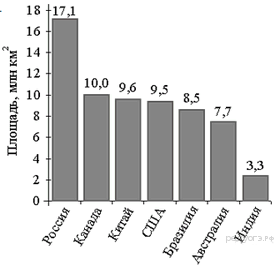 На диаграмме представлены семь крупнейших по площади территории (в млн км2) стран мира.
На диаграмме представлены семь крупнейших по площади территории (в млн км2) стран мира.
Какое из следующих утверждений верно?
1) Монголия входит в семёрку крупнейших по площади территории стран мира.
2) Площадь территории Индии составляет 8,5 млн км2.
3) Площадь Австралии больше площади Канады.
4) Площадь Канады больше площади Индии более, чем в 3 раза.
В ответе запишите номер выбранного утверждения.
19. Стрелок три раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,6. Найдите вероятность того, что стрелок первый раз попал в мишени, а последние два раза промахнулся.
20. Длину окружности 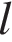 можно вычислить по формуле
можно вычислить по формуле 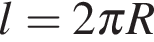 , где
, где 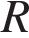 — радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус окружности, если её длина равна 78 м. (Считать
— радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус окружности, если её длина равна 78 м. (Считать  ).
).
21. Решите уравнение
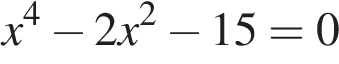
22. Дорога между пунктами A и В состоит из подъёма и спуска, а её длина равна 14 км. Турист прошёл путь из А в В за 4 часа, из которых спуск занял 2 часа. С какой скоростью турист шёл на спуске, если его скорость на подъёме меньше его скорости на спуске на 3 км/ч?
23. Постройте график функции  и определите, при каких значениях
и определите, при каких значениях  прямая
прямая  имеет с графиком ровно одну общую точку.
имеет с графиком ровно одну общую точку.
24. Основания трапеции равны 9 и 15. Найдите отрезок, соединяющий середины диагоналей трапеции.
25. Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD = 10. Докажите, что треугольники CBD и ADB подобны.
26. Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 40:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 30.








 В треугольнике ABC угол A равен 90°, AC = 6, sin B = 0,3. Найдите BC.
В треугольнике ABC угол A равен 90°, AC = 6, sin B = 0,3. Найдите BC. В угол C величиной 79° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.
В угол C величиной 79° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах. Основания трапеции равны 1 и 13, одна из боковых сторон равна
Основания трапеции равны 1 и 13, одна из боковых сторон равна  Найдите тангенс угла AOB, изображенного на рисунке.
Найдите тангенс угла AOB, изображенного на рисунке.
 На диаграмме представлены семь крупнейших по площади территории (в млн км2) стран мира.
На диаграмме представлены семь крупнейших по площади территории (в млн км2) стран мира.



















