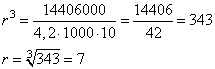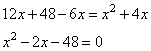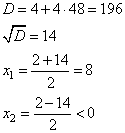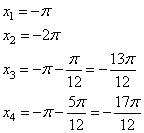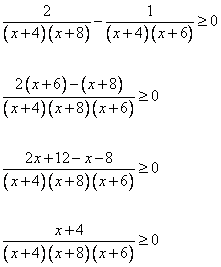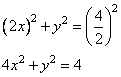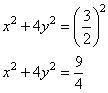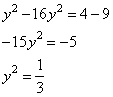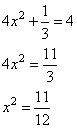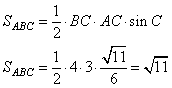Вариант1. ЕГЭ 2021 11класс решение

Задание 1. В школе есть трёхместные туристические байдарки. Какое наименьшее число байдарок нужно взять в поход, в котором участвует 25 человек?

Решение.

Нужно определить сколько групп не более чем из 3 человек составляют 25 человек, получим:

,

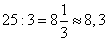т.е. 9 групп (8 из 3 человек и 1 из одного). Значит, нужно 9 байдарок.

Ответ: 9.

Задание 2. На диаграмме показано распределение выплавки алюминия в 11 странах мира (в тысячах тонн) за 2009 год. Среди представленных стран первое место по выплавке алюминия занимала Франция, одиннадцатое место — Казахстан. Какое место занимала Словакия?

Решение.

Первое место принадлежит Франции и ее столбец на рисунке самый высокий. Чтобы определить место, занимаемое Словакией, нужно подсчитать сколько столбцов, больше, чем столбец Словакия имеется на графике. Из рисунка видим, что таких столбцов 9, значит, Словакия занимает 10-е место.

Ответ: 10.

Задание 3. Найдите площадь параллелограмма, вершины которого имеют координаты (1; 7), (4; 3), (4; 5), (1;9).

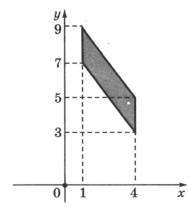
Решение.

Площадь параллелограмма определяется как произведение длины (по координате  )  на ширину (по координате  ). То есть площади аналогичного прямоугольника, если выронить параллелограмм до прямых углов (площадь от этого не изменится). Из рисунка видно, что ширина составляет 2 единицы, а длина 4-1=3 единицы. Таким образом, площадь параллелограмма равна:

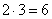 кв. единиц

Ответ: 6.

Задание 4. Два завода выпускают одинаковые автомобильные предохранители. Первый завод выпускает 40% предохранителей, второй — 60%. Первый завод выпускает 4% бракованных предохранителей, а второй — 3%. Найдите вероятность того, что случайно выбранный в магазине предохранитель окажется бракованным.

Решение.

Выбранный бракованный предохранитель может быть выпущен или первым или вторым заводом. Процент брака от первого завода. Его доля в продукции составляет 40% и среди них 4% брака, следовательно, процент брака от первого завода во всей продукции составляет

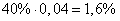
Для второго соответственно получаем

.

В сумме брака в продукции 1,6%+1,8%=3,4%. Тогда вероятность выбора бракованного изделия будет равна

.

Ответ: 0,034.

Задание 5. Найдите корень уравнения  .

Решение.

Прологарифмируем обе части уравнения:

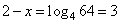
Находим корень уравнения

Ответ: -1.

Задание 6. В треугольнике ABC AC = ВС = 12,  . Найдите АВ.

Решение.

Рассмотрим равнобедренный треугольник  .

Из вершины   опущена высота на основание   так, что  .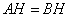

Синус угла – это отношение противолежащего катета на гипотенузу и для угла 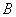  можем записать:

.

Вместе с тем, из прямоугольного треугольника 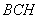  катет 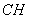  можно записать так:

Возведем синус в квадрат и вместо катета   подставим выражение выше, получим:

Учитывая, что  , получаем:

.

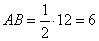Ответ: 6.

Задание 7. Функция у = f(x) определена на интервале (-5; 6). На рисунке изображён график функции у=f(x). Найдите среди точек   те точки, в которых производная функции f(x) равна нулю. В ответ запишите количество найденных точек.

Решение.

Производная – это тангенс угла наклона касательной к оси OX, проведенной в точке взятия производной. Значение производной будет равно нулю в точках максимума и минимума функции (в точках экстремума функции). Найдем такие точки среди точек  . Анализ рисунка показывает, что это точки 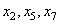 , т.е. 3 точки.

Ответ: 3.

Задание 8. Во сколько раз увеличится объем куба, если все ребра увеличить в 8 раз?

Задание 9. Найдите значение выражения  .

Решение.

Упростим и вычислим выражение, получим:

Ответ: 14.

Задание 10. На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле:  , где   = 4,2 — постоянная, r — радиус аппарата в метрах, 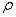  = 1000 кг/м3 — плотность воды, a g — ускорение свободного падения (считайте g = 10 Н/кг). Найдите радиус аппарата, если выталкивающая сила при погружении равна 14 406 000 Н? Ответ дайте в метрах.

Решение.

В задаче дана величина силы Архимеда и формула связи силы Архимеда с радиусом аппарата, следовательно, радиус аппарата можно найти по формуле:

,

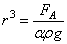откуда имеем:

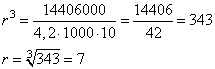
То есть радиус аппарата равен 7 метрам.

Ответ: 7.

Задание 11. На изготовление 48 деталей первый рабочий тратит на 8 часов меньше, чем второй рабочий на изготовление 96 таких же деталей. Известно, что первый рабочий за час делает на 4 детали больше, чем второй. Сколько деталей в час делает второй рабочий?

Решение.

Обозначим через   число деталей, которые делает второй рабочий за один час. Соответственно первый рабочий делает 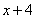  детали в час. Таким образом, первый рабочий 48 деталей сделает за  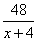 часов, а второй рабочий 96 деталей сделает за   часов. Известно, что первый рабочий закончит свою работу на 8 часов раньше второго, получаем уравнение:

,

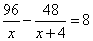делим обе части уравнения на 8, имеем:

,

откуда

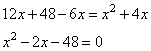
Решаем квадратное уравнение, получаем:

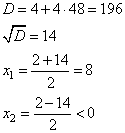
Таким образом, скорость второго рабочего составляет 8 деталей в час.

Ответ: 8.

Задание 12. Найдите наибольшее значение функции y=4tgx – 4x + π – 6 на отрезке  .

Решение.

1. Наименьшее значение функции может быть либо на границах интервала, либо в точках экстремума, принадлежащих этому интервалу. Найдем точки экстремума. Для этого вычислим производную функции и приравняем ее нулю, получим:

Имеем два уравнения

 - не принадлежит 

и

2. Вычислим значения функции на границах интервала и в точке экстремума, получим:

Наибольшее значение функции равно -2.

Задание 13. а) Решите уравнение  .

б) Найдите все корни этого уравнения, принадлежащие промежутку [-2π; -π].

Решение.

а) Перепишем уравнение в виде

,

и положим  . Умножим уравнение на 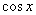 , получим:

Получаем два уравнения:

б) С помощью числовой окружности выберем корни уравнения на промежутке [-2π; -π]. Получим числа (см. рисунок):

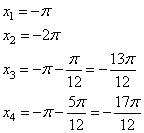
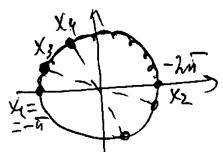
Ответ: а) 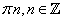 ;  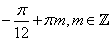;  ; б)  .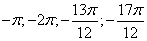

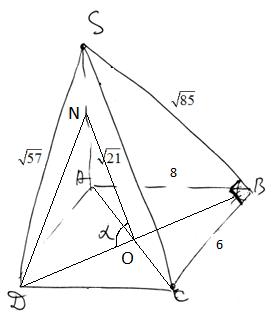
Задание 14. В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами АВ = 8 и ВС = 6. Длины боковых рёбер пирамиды SA = √21, SB = √85 , SD = √57.

а) Докажите, что SA — высота пирамиды.

б) Найдите угол между прямыми SC и BD.

Решение.

а) Рассмотрим треугольник SAB. Из значения его сторон следует, что

,

Следовательно, SB – гипотенуза и угол SAB – прямой.

Аналогично для треугольника SAD:

,

получаем, что SD – гипотенуза и угол SAD – прямой. В результате получаем, что при   и 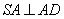 , следует   (по признаку перпендикулярности прямой и плоскости), и следовательно, SA – высота пирамиды.

б) Угол между прямыми SC и BD – это угол между двумя скрещивающимися прямыми, который соответствует углу   между прямыми NO и OD (см. рисунок). Так как прямая   и точка O делит прямую AC пополам, то и точка N будет делить AS пополам. Следовательно, ON – это средняя линия треугольника ASC и равна

.

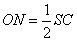Вычислим диагональ AC из прямоугольного треугольника ACD:

.

Тогда длина ребра SC будет равна (учитывая, что треугольник SAC прямоугольный):

и

.

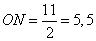Так как диагонали в прямоугольнике равны, то BD=AC. Тогда

.

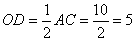Найдем длину отрезка DN. Рассмотрим прямоугольный треугольник SAD, в котором катет  , катет 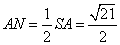  и по теореме Пифагора имеем

.

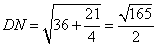По теореме косинусов находим косинус угла  , получаем:

откуда

.

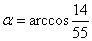Задание 15. Решите неравенство  .

Решение.

Упростим неравенство, приведем его к следующему виду:

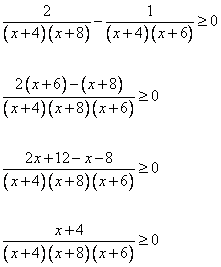
Получаем следующие точки, делящие числовую ось:

.

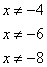
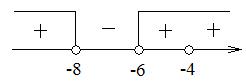
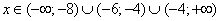Ответ:  .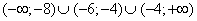

Задание 16. Медианы AM и BN треугольника ABC перпендикулярны и пересекаются в точке Р.

а) Докажите, что CP = АВ.

б) Найдите площадь треугольника ABC, если известно, что АС = 3 и ВС = 4.

Решение.

а) Рассмотрим треугольник ABC, в котором отмечены медианы AM, BN и CF. Медианы пересекаются в одной точке P и делятся этой точкой в отношении 2:1, считая от вершины. То есть можно записать, что CP=2FP. Учитывая, что точка F находится на середине отрезка AB и треугольник APB прямоугольный (по условию задания), то точка F является центром описанной окружности вокруг треугольника APB. Следовательно, отрезки AF, FB, FP – радиусы этой окружности, и AB=2FP. Но так как 2FP=2PC, то AB=PC.

б) Пусть   и  , соответственно,   и 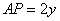 . Рассмотрим прямоугольный треугольник BPM (так как  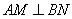). В соответствии с теоремой Пифагора можно записать равенство:

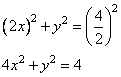
Аналогично, из прямоугольного треугольника APN, имеем:

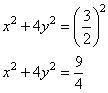
Получаем систему уравнений:

Умножим второе уравнение на 4 и вычтем его из первого, получим:

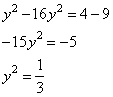
Подставляя полученное значение в первое уравнение, имеем:

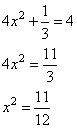
Рассмотрим прямоугольный треугольник APB, в котором гипотенуза AB равна

Найдем косинус угла   из треугольника ABC по теореме косинусов:

тогда

.

Наконец, площадь треугольника ABC равна:

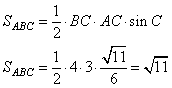
Ответ:  .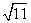

Задание 17. 15-го января планируется взять кредит в банке на 21 месяц. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.

Сколько процентов от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь срок кредитования?

Решение.

Обозначим через   сумму кредита, взятого в банке. В первый месяц она увеличивается на 3% и становится равной 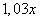 . После этого делается платеж такой, чтобы долг был равен  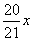 (равномерно уменьшался), получаем сумму платежа:

.

В следующий месяц сумма 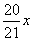  увеличивается до  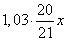 и сумма платежа составляет (чтобы осталось  ):

.

Таким образом, за все 21 месяцы сумма выплат составит

То есть сумма выплат увеличивается на 33% по сравнению с исходным размером кредита.

Ответ: 33.

Задание 19. Учитель пишет примеры на сложение трёх натуральных чисел так, чтобы во всех примерах ответ был один и тот же N, при этом он хочет, чтобы все слагаемые во всех примерах (даже в различных примерах) были различны.

а) Можно ли написать два таких примера, если N = 15?

б) Можно ли написать 8 таких примеров, если N = 55?

в) Можно ли написать 12 таких примеров, если N = 55?

Решение.

а) Чтобы написать примеры с различными натуральными числами, первые два числа будем перебирать по порядку, а третье число вычислять как разность между N и двумя первыми числами, получим:

1+2+12=15

3+4+8=15

б) По аналогии попробуем записать 8 примеров для N=55 с различными натуральными слагаемыми:

1+2+52=55

3+4+48=55

5+6+44=55

7+8+40=55

9+10+36=55

11+12+32=55

13+14+28=55

15+16+24=55

в) Если продолжить запись примеров, получим:

17+18+20=55

19+20+16=55

Как видим в 10-м примере начинаются повторения слагаемых, т.е. записать 12 примеров невозможно.

Ответ: а) да; б) да; в) нет.