Векторы и координаты в пространстве

Векторы и координаты в пространстве.

Выполнила: Кузнецова Ольга, студентка ГАУ КО ПОО КСТ

Система координат в пространстве

Систе́ма координа́т — комплекс определений, реализующий метод координат, то есть способ определять положение и перемещение точки или тела с помощью чисел или других символов. 

Три попарно перпендикулярные прямые с выбранными направлениями и единицей измерения образуют систему координат в пространстве. Точка пересечения всех прямых является началом системы координат. 

Расстояние от точки А (x;y;z) до координатных осей :

• До оси x = +
• До оси y = +
• До оси z = +

Расстояние от точки А до плоскости?

• До плоскости xy = |z|
• До плоскости xz = |y|
• До плоскости yz = |x|

Расстояние между двумя точками

• Представим точку А(x-1;y-1;z-1)
• точка В(x-2;y-2;z-2)
• Тогда мы найдем длину отрезка АВ по формуле =
• ++
• Как найти середину отрезка?
• С= ;
• Кстати! 0 - это нулевой вектор, его начало совпадает с концом!

Подумаем.

• Даны точки : А(3;2;-2) и В(2;4;3). Найдите длину отрезка АВ.
• +(+(++= 1+4+1=
• Ответ =

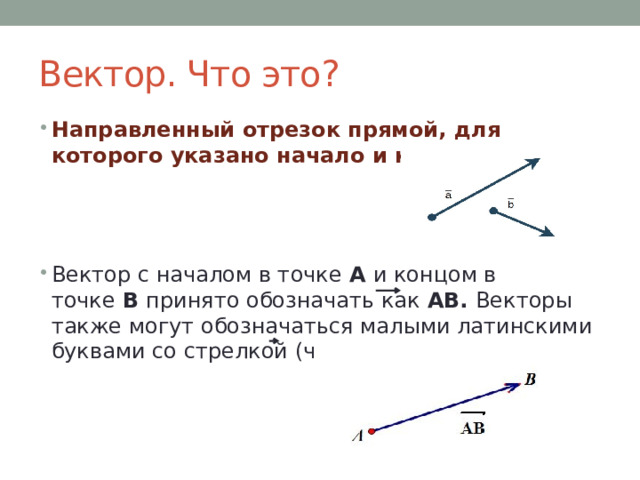
Вектор. Что это?

• Направленный отрезок прямой, для которого указано начало и конец.

• Вектор с началом в точке  А  и концом в точке  В  принято обозначать как  АВ. Векторы также могут обозначаться малыми латинскими буквами со стрелкой (черточкой) а

Определения

Абсолютная величина (модуль) вектора – длина отрезка соединяющего вектор.

Два вектора называются равными, если они совмещаются параллельным переносом.

!Равные вектора, это те, которые одинаково направленны и равны по абсолютной величине!

Равные вектора имеют равные соответствующие координаты

Что такое коллинеарные вектора?

• Коллинеарные вектора сонаправленны и лежат на параллельных прямых или на одной прямой.
• Вектора коллинеарны тогда, когда их координаты пропорцианальны

Координаты вектора в пространстве

• Чтобы найти координаты вектора, заданного двумя точками, нужно от координат конечной точки, вычесть координаты начальной точки.
• !координаты вектора записываются в фигурных скобках!
• Формула

Длина вектора

• а {x;y;z}(модель вектора) равна корню квадратному из суммы квадратов его координат
• = ++

Сложение и вычитание векторов

а + в = с {xA + xB; yA + yB; zA + zB}

а - в = с {xA - xB; yA - yB; zA - zB}

Умножение вектора на число

В результате умножения получается новый вектор

K*a = Ka {K*x;K*y;K*z}

Скалярное произведение векторов. Угол между векторами

• При скалярном произведении получается число!
• Формула : а * в = xA*xB;yA*yB;zA*zB
• Так же СП называется число, равное произведению длин этих векторов на косинус угла между ними
• а * в = ** Тогда,
• Если два вектора перпендикулярны, то их скалярное произведение равно 0.
• Если угол острый / тупой