Вектор – это величина, которая характеризуется не только значением, но и направлением. Иными словами, это направленный отрезок.
Но кроме его длины, нам также важно, где находится его начало, а где конец.
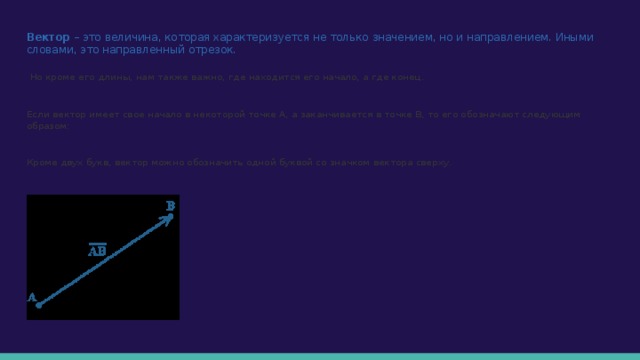
Если вектор имеет свое начало в некоторой точке А, а заканчивается в точке В, то его обозначают следующим образом:
Кроме двух букв, вектор можно обозначить одной буквой со значком вектора сверху.
Просмотр содержимого документа
«Векторы. Модель вектора.»

Векторы. Модель вектора. Равенство векторов. Сложение векторов. Умножение вектора на число.
Шулимова С.А.
ОДЛ 118
Вектор – это величина, которая характеризуется не только значением, но и направлением. Иными словами, это направленный отрезок.
Но кроме его длины, нам также важно, где находится его начало, а где конец.
Если вектор имеет свое начало в некоторой точке А, а заканчивается в точке В, то его обозначают следующим образом:
Кроме двух букв, вектор можно обозначить одной буквой со значком вектора сверху.

Если длина некоторого вектора равна единичному отрезку, то его называют единичным .
Если некоторые векторы расположены на одной прямой или же параллельны друг другу, то такие векторы называются коллинеарными .
Если некоторые векторы можно назвать коллинеарными, но кроме этого они направлены в одну сторону, то их можно назвать сонаправленными .

Если же наоборот два коллинеарных вектора смотрят в разные стороны, то их называют противоположно направленными .
Если же некоторые векторы являются коллинеарными, сонаправленными, а также имеют одинаковую длину (модуль), то их можно назвать равными .

Модуль вектора
Длиной вектора (его модулем) называют расстояние между концом вектора и его началом.
Для определения модуля вектора следует воспользоваться следующей формулой:
Кроме этого, модуль вектора может обозначаться следующим образом:
Если некоторый вектор имеет начало и конец в одной и той же точке, то такой вектор называют нулевым. Нулевой вектор обозначают, как

Если вектор задан, например, в двумерном пространстве, своими координатами , то его модуль равен корню квадратному из суммы квадратов координат:
Пример нахождения модуля векторов

Равенство векторов

Если векторы заданы своими координатами, то они равны , если равны их соответствующие координаты:

Сложение векторов
Чтобы сложить два вектора для получения нового, необходимо сложить соответствующие координаты.
Например, сложим вектор {2;3} с вектором {5;7}. В результате получим новый вектор с координатами {7;10}. С вычитанием все аналогично.



Умножение вектора
Чтобы умножить вектор на некоторое число, следует умножить каждую его координату на данное число.
Свойства:
- Первоначальный вектор и вектор умноженный на некоторое число, который равный ему, являются параллельными.
- Если число, на которое умножался вектор, больше нуля, то новый вектор будет сонаправлен первоначальному. Если же число меньше нуля, то векторы будут противоположно направленны.





























