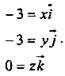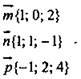1
Тема. Векторы в пространстве.
Координаты вектора
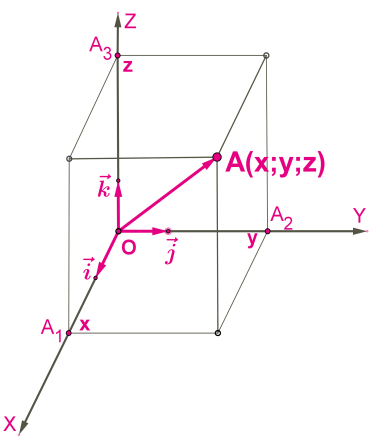
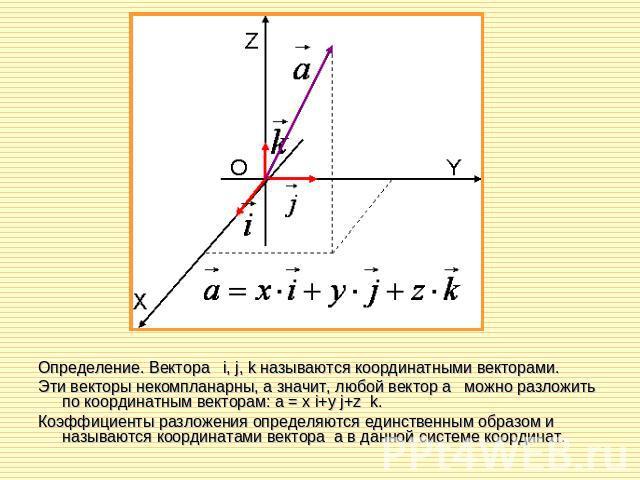
Если в системе координат от начальной точки отложить единичные векторы i⃗ , j⃗ и k⃗ , то можно определить прямоугольный базис. Любой вектор можно разложить по единичным векторам и представить в виде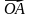 =x⋅i⃗ +y⋅j⃗ +z⋅k⃗ .
=x⋅i⃗ +y⋅j⃗ +z⋅k⃗ .
Коеффициенты x, y и z определяются одним единственным образом и называются координатами вектора.
Записываются так: 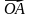 {x;y;z}.
{x;y;z}.
Рассмотрим правила о том, как с помощью координат записать:
- координаты суммы векторов, если даны координаты векторов:
a⃗ {x1;y1;z1}, b⃗ {x2;y2;z2}, a⃗ +b⃗ {x1+x2;y1+y2;z1+z2}
- координаты разности векторов, если даны координаты векторов:
a⃗ −b⃗ {x1−x2;y1−y2;z1−z2}
- координаты произведения вектора на число, если даны координаты вектора:
n⋅a⃗ {n⋅x1;n⋅y1;n⋅z1}
- длину вектора:
∣a⃗ ∣=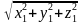
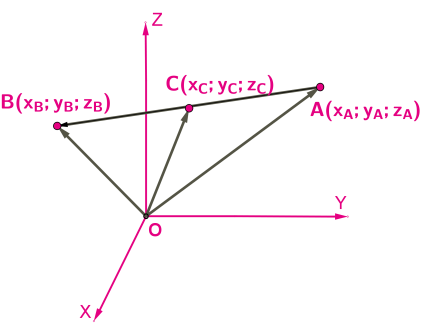
- координаты вектора, если даны координаты начальной и конечной точки вектора:
A(xA;yA;zA), B(xB;yB;zB), 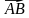 {xB−xA;yB−yA;zB−zA}
{xB−xA;yB−yA;zB−zA}
- расстояние между двумя точками, если даны координаты точек:
∣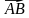 ∣=|AB
∣=|AB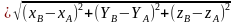 −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−√
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−√
- координаты серединной точки отрезка, если даны координаты начальной и конечной точки отрезка:
xC=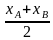 ; yC=
; yC=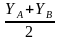 ; zC=
; zC=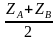 ;
;
| Коллинеарные векторы  Ненулевые векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. | Компланарные векторы 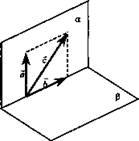 Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости. |
г) Дано: 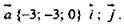
Установить: компланарность данных векторов.
Решение: Если вектор 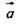 можно разложить по векторам
можно разложить по векторам 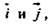 то векторы
то векторы 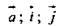 компланарны,
компланарны, 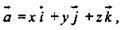
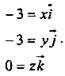
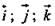 - единичные векторы. х = -3; у = -3; z = 0. (Ответ:
- единичные векторы. х = -3; у = -3; z = 0. (Ответ: 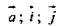 – компланарные векторы.)
– компланарные векторы.)
д) Дано: 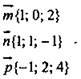
Установить: компланарность данных векторов.
Решение:
1. Векторы 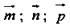 неколлинеарные, так как координаты этих векторов не пропорциональные друг другу числа.
неколлинеарные, так как координаты этих векторов не пропорциональные друг другу числа.
2. 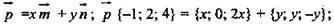
(неверно, так как - 8 ≠ 4).
Ответ: 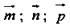 - некомпланарные векторы.
- некомпланарные векторы.









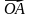 =x⋅i⃗ +y⋅j⃗ +z⋅k⃗ .
=x⋅i⃗ +y⋅j⃗ +z⋅k⃗ .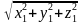

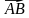 {xB−xA;yB−yA;zB−zA}
{xB−xA;yB−yA;zB−zA}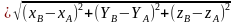 −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−√
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−√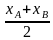 ; yC=
; yC=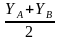 ; zC=
; zC=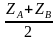 ;
;