Просмотр содержимого документа
«Векторы в пространстве»

Векторы в пространстве
МОУ «ГУМАНИТАРНАЯ ГИМНАЗИЯ №33 г. ДОНЕЦКА»
Учитель математики
Старостенко И.С.
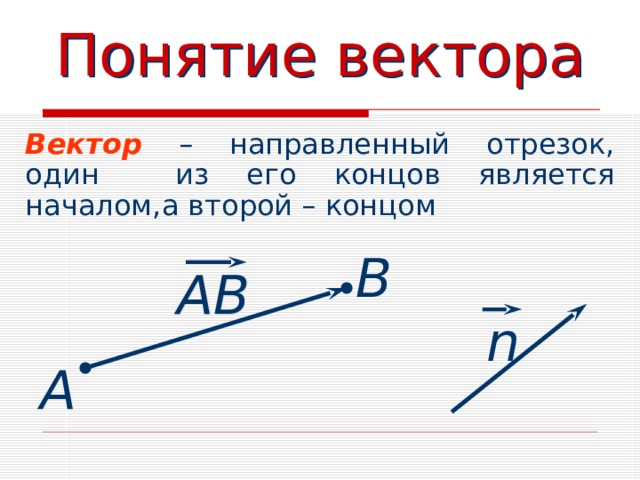
Понятие вектора
Вектор – направленный отрезок, один из его концов является началом,а второй – концом
В
АВ
n
А

Нулевой вектор
Любая точка на плоскости может рассматриваться как вектор.
Такой вектор называется нулевым .
М
ММ = 0

Длина вектора
Длиной ненулевого вектора АВ
называется длина отрезка АВ .
В
а
АВ = а
0
А
0 = 0
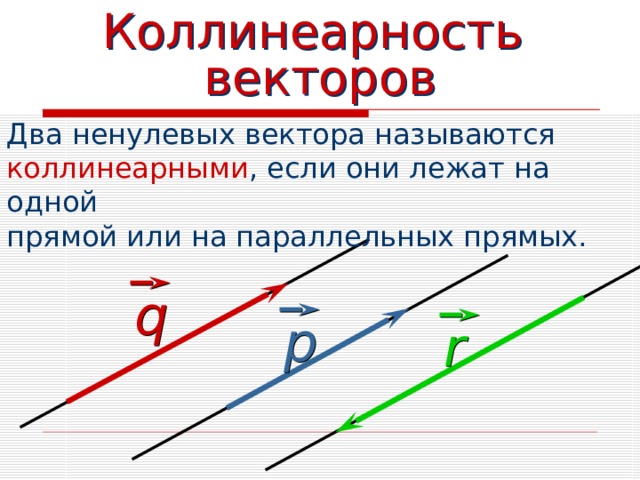
Коллинеарность векторов
Два ненулевых вектора называются
коллинеарными , если они лежат на одной
прямой или на параллельных прямых.
q
р
r
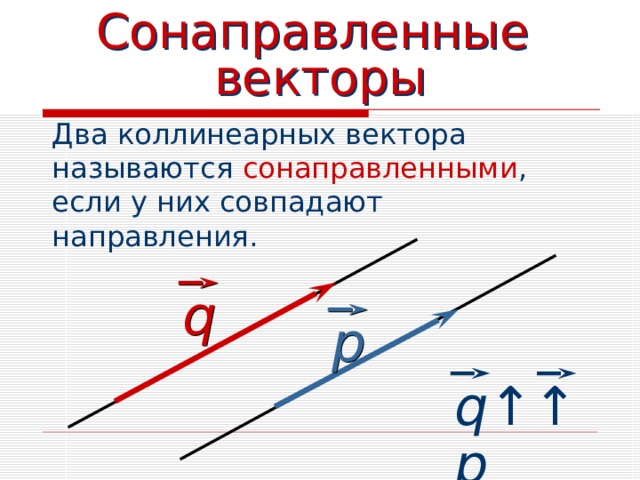
Сонаправленные векторы
Два коллинеарных вектора
называются сонаправленными ,
если у них совпадают направления.
q
р
q↑↑ р

Противоположно направленные векторы
Два коллинеарных вектора называются
противоположно направленными , если
они не сонаправлены.
а
b
a↑↓b
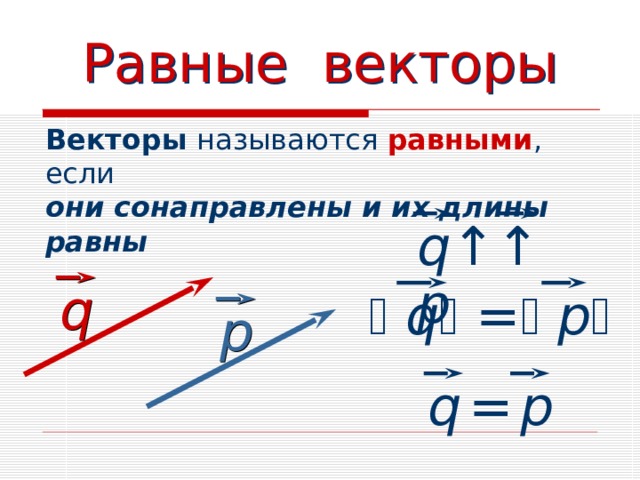
Равные векторы
Векторы называются равными , если
они сонаправлены и их длины равны
q↑↑ р
q
q = р
р
q = р
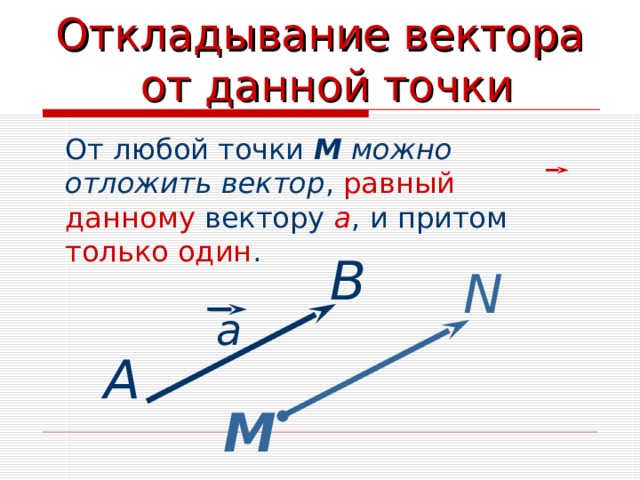
Откладывание вектора от данной точки
От любой точки М можно отложить вектор , равный данному вектору а , и притом только один .
В
N
a
А
М

Действия над векторами
х
-
+

ПРАВИЛА И СВОЙСТВА СЛОЖЕНИЯ ВЕКТОРОВ
р
+
q
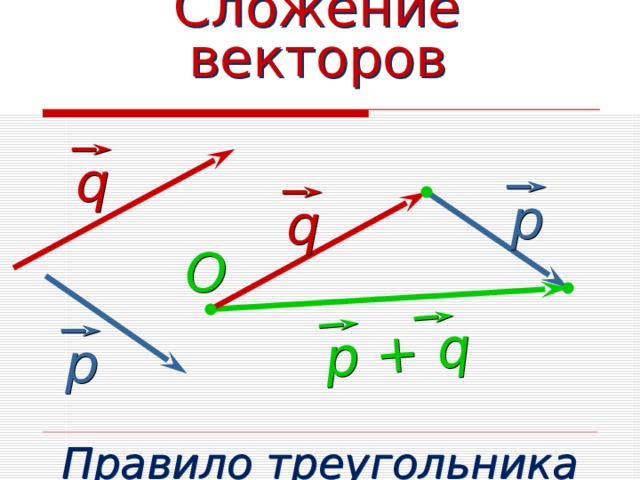
р + q
Сложение векторов
q
р
q
O
р
Правило треугольника
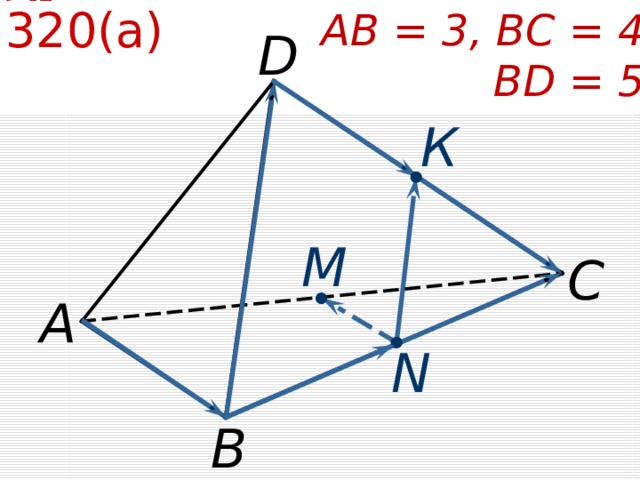
№ 320(а)
АВ = 3, ВС = 4
BD = 5
D
К
M
С
А
N
В
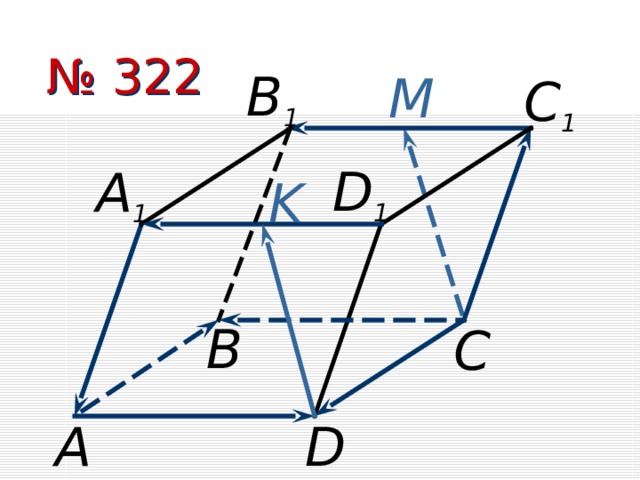
№ 322
B 1
M
C 1
D 1
А 1
K
В
С
А
D
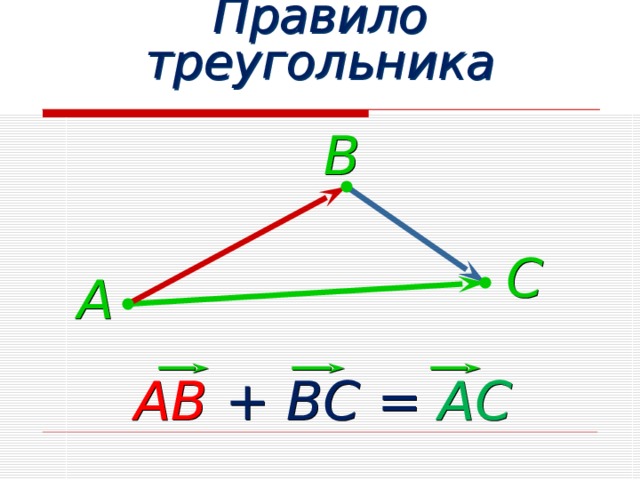
Правило треугольника
В
С
А
АВ + ВС = АС
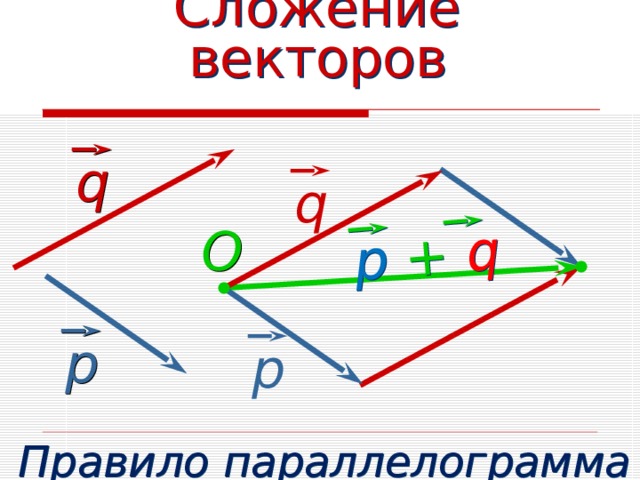
р + q
Сложение векторов
q
q
O
р
р
Правило параллелограмма
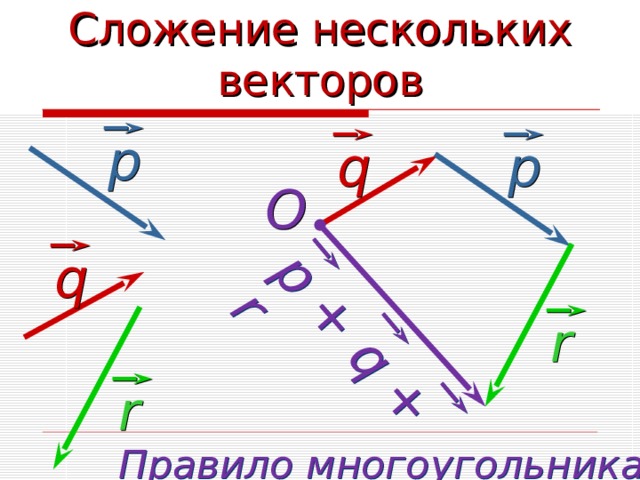
Сложение нескольких векторов
р + q + r
р
q
р
O
q
r
r
Правило многоугольника

Свойства сложения
а + b
b + a
=
− переместительный закон
( b + с) + a
(а + b ) + с
=
− сочетательный закон
а − b
a + (− b)
=
− разность векторов
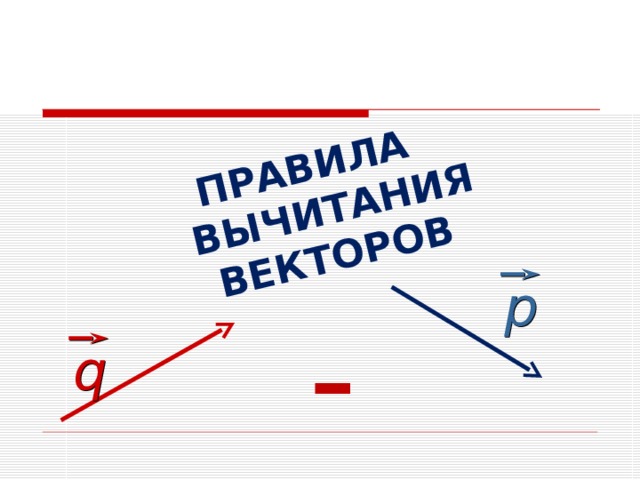
ПРАВИЛА ВЫЧИТАНИЯ ВЕКТОРОВ
р
-
q
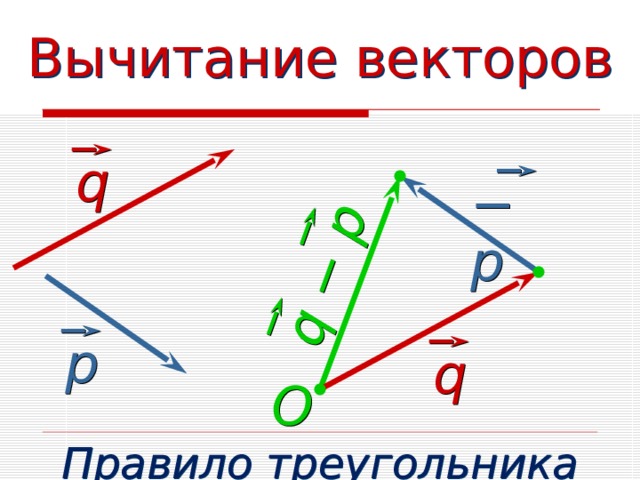
q − p
Вычитание векторов
q
− р
р
q
O
Правило треугольника
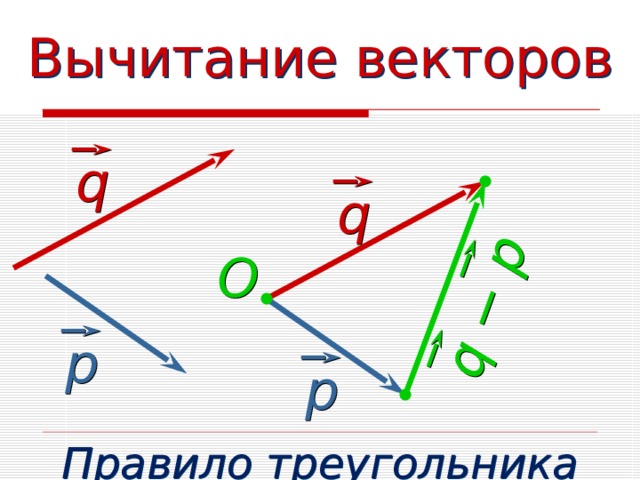
q − p
Вычитание векторов
q
q
O
р
р
Правило треугольника
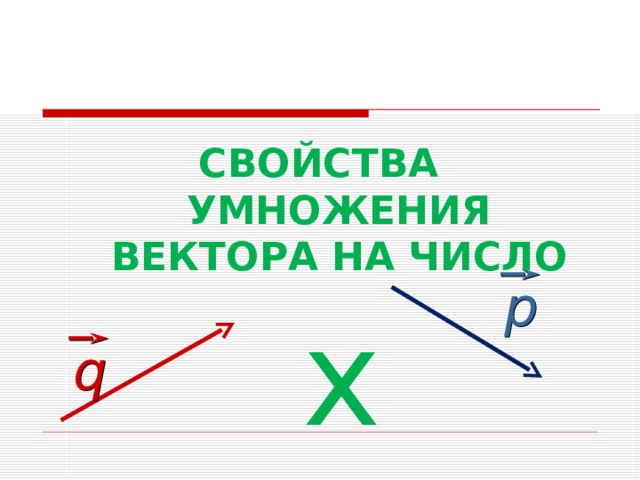
СВОЙСТВА УМНОЖЕНИЯ ВЕКТОРА НА ЧИСЛО
р
х
q
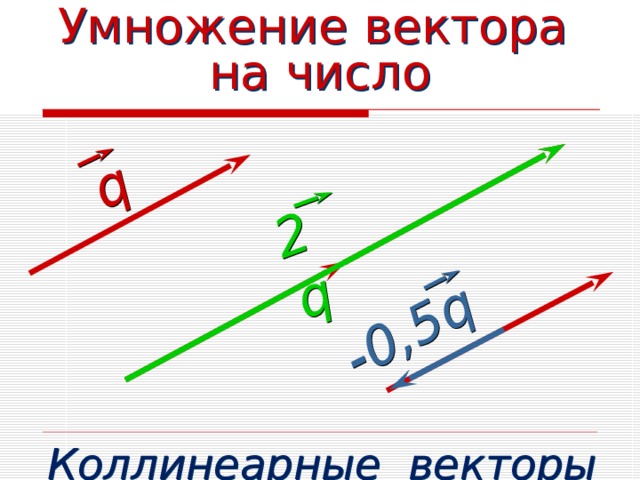
Умножение вектора на число
q
2 q
-0,5 q
Коллинеарные векторы

Свойства умножения
(k n) а
k(n a)
=
− сочетательный закон
ka + kb
k (а + b )
=
− первый распределительный закон
( k + n) а
ka + na
=
− второй распределительный закон
![Использованы ресурсы Геометрия. 10 – 11 классы: учеб. для общеобразоват. учреждений: базовый и профил. уровни / [ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. ]. – М.: Просвещение, 2018. Саакян С.М., Бутузов В.Ф. Изучение геометрии в 10 – 11 классах: Методические рекомендации к учебнику. Книга для учителя. – М.: Просвещение, 2003. Геометрия. Поурочные разработки. 10 – 11 классы: Учебно пособие для общеобразоват. организаций/ С.М. Саакян, В.Ф. Бутузов. – М.: Просвещение, 2015.](https://fsd.multiurok.ru/html/2020/11/07/s_5fa6d7d88e61d/img24.jpg)
Использованы ресурсы
- Геометрия. 10 – 11 классы: учеб. для общеобразоват. учреждений: базовый и профил. уровни / [ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. ]. – М.: Просвещение, 2018.
- Саакян С.М., Бутузов В.Ф. Изучение геометрии в 10 – 11 классах: Методические рекомендации к учебнику. Книга для учителя. – М.: Просвещение, 2003.
- Геометрия. Поурочные разработки. 10 – 11 классы: Учебно пособие для общеобразоват. организаций/ С.М. Саакян, В.Ф. Бутузов. – М.: Просвещение, 2015.































![Использованы ресурсы Геометрия. 10 – 11 классы: учеб. для общеобразоват. учреждений: базовый и профил. уровни / [ Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. ]. – М.: Просвещение, 2018. Саакян С.М., Бутузов В.Ф. Изучение геометрии в 10 – 11 классах: Методические рекомендации к учебнику. Книга для учителя. – М.: Просвещение, 2003. Геометрия. Поурочные разработки. 10 – 11 классы: Учебно пособие для общеобразоват. организаций/ С.М. Саакян, В.Ф. Бутузов. – М.: Просвещение, 2015.](https://fsd.multiurok.ru/html/2020/11/07/s_5fa6d7d88e61d/img24.jpg)










