Вероятность. Готовимся к ОГЭ и ЕГЭ

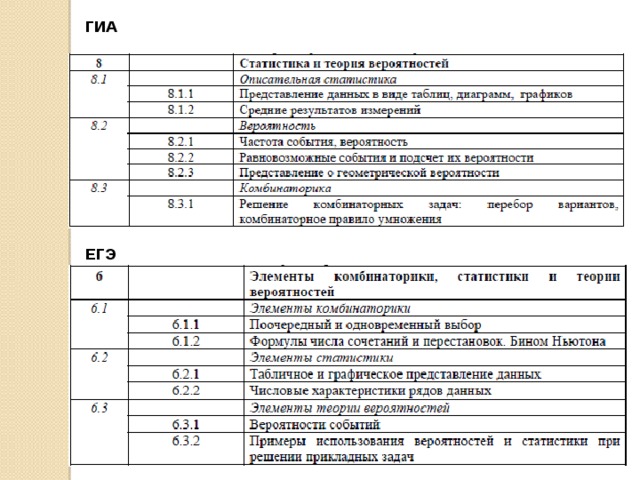
ГИА

ЕГЭ

ГИА.

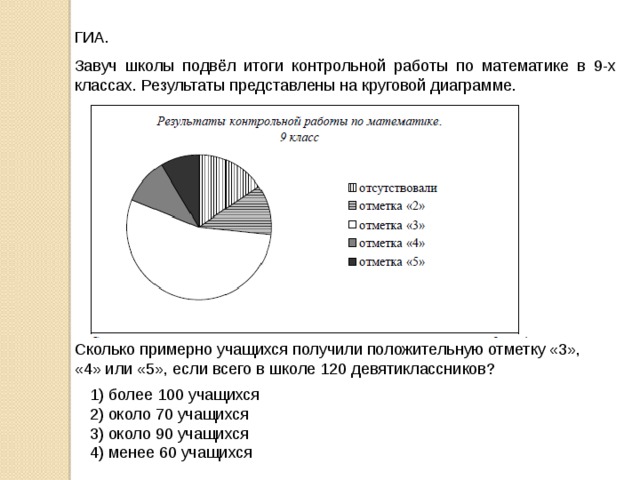
Завуч школы подвёл итоги контрольной работы по математике в 9-х классах. Результаты представлены на круговой диаграмме.

Сколько примерно учащихся получили положительную отметку «3», «4» или «5», если всего в школе 120 девятиклассников?

1) более 100 учащихся

2) около 70 учащихся

3) около 90 учащихся

4) менее 60 учащихся

1. Определите по диаграмме, в каких пределах находится содержание углеводов.

1) 0-20% 2) 20-50% 3) 50-70% 4) 70-100%

2. Определите по диаграмме, содержание каких веществ преобладает.

1) белки 2) жиры 3) углеводы 4) прочее

3. Определите по диаграмме, содержание каких веществ наименьшее.

1) белки 2) жиры 3) углеводы 4) прочее

4. Определите по диаграмме, сколько примерно белков содержится в 500 граммах риса.

1) около 7 г 2) около 35 г 3) около 70 г 4) около 350 г

5. Определите по диаграмме, какая примерно масса риса содержит 300 граммов углеводов.

1) около 220 г 2) около 400 г 3) около 1,5 кг 4) около 3 кг

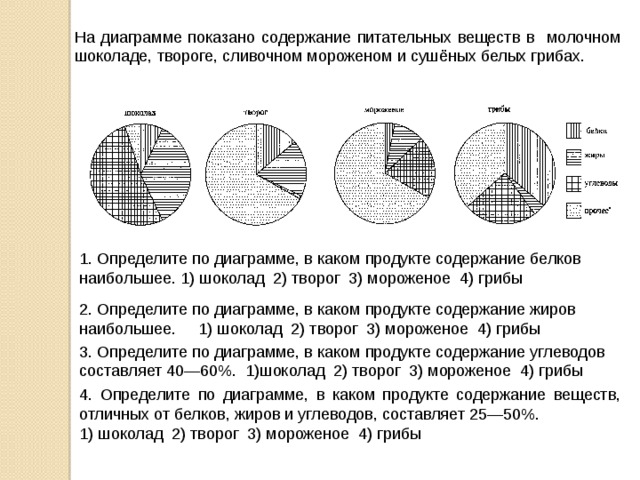
На диаграмме показано содержание питательных веществ в молочном шоколаде, твороге, сливочном мороженом и сушёных белых грибах.

1. Определите по диаграмме, в каком продукте содержание белков наибольшее. 1) шоколад 2) творог 3) мороженое 4) грибы

2. Определите по диаграмме, в каком продукте содержание жиров наибольшее. 1) шоколад 2) творог 3) мороженое 4) грибы

3. Определите по диаграмме, в каком продукте содержание углеводов составляет 40—60%. 1)шоколад 2) творог 3) мороженое 4) грибы

4. Определите по диаграмме, в каком продукте содержание веществ, отличных от белков, жиров и углеводов, составляет 25—50%.

1) шоколад 2) творог 3) мороженое 4) грибы

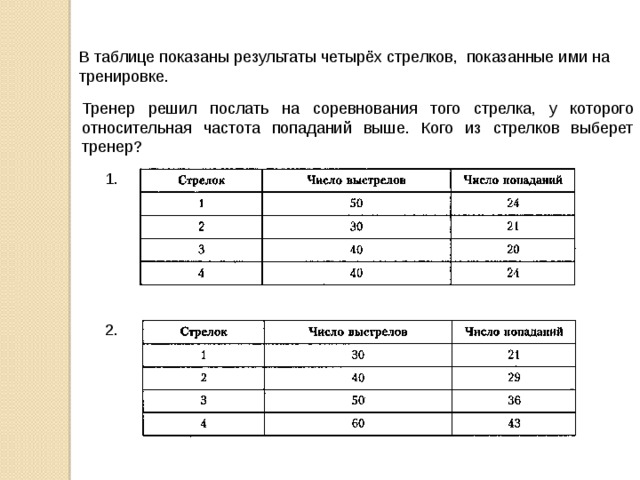
В таблице показаны результаты четырёх стрелков, показанные ими на тренировке.

Тренер решил послать на соревнования того стрелка, у которого относительная частота попаданий выше. Кого из стрелков выберет тренер?

1.

2.

Вероятность события. Вероятностью события А называется отношение числа m благоприятствующих этому событию исходов к общему числу n равновозможных элементарных исходов испытания:

Элементарные события (элементарные исходы) опыта — простейшие события, которыми может окончиться случайный опыт. Сумма вероятностей всех элементарных событий опыта равна 1.

Р авновозможные события. События называются равновозможными,

если есть основания считать, что ни одно из этих событий не является

более возможным, чем другие, т.е. все события имеют равные «шансы».

Противоположное событие. Событие A, состоящее из тех и только тех элементарных исходов опыта, которые не входят в A, называется противоположным событию А.

.

Алгоритм решения задач,

в которых рассматриваются опыты с равновозможными элементарными исходами:

1. Определить, что является элементарным событием (исходом) в данном случайном эксперименте (опыте).

2. Найти общее число элементарных событий N.

3. Определить, какие элементарные события благоприятствуют интересующему нас событию A, и найти их число N(A).

4. Найти вероятность события A по формуле

Пример 1. Вася, Петя, Коля и Леша бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет Леша.

Пример 2. Оля, Денис, Коля, Витя и Света бросили жребий — кому

начинать игру. Найдите вероятность того, что начинать игру должен

будет мальчик.

Пример 3. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что решка выпадет ровно один раз.

Пример 4. Найдите вероятность того, что при броске трёх симметричных монет два раза выпадет орёл, а один раз решка.

Пример 5. Найдите вероятность того, что при броске игрального кубика выпадет 2 или 5. Результат округлите до сотых.

Пример 6. Оля и Вадим играют в кости. Они бросают кость по одному разу. Выигрывает тот, у кого больше очков. Считается, что у ребят ничья, если очков они выбросили поровну. Оля выкинула 4 очка. Затем кубик бросает Вадим. Найдите вероятность того, что Вадим не проиграет.

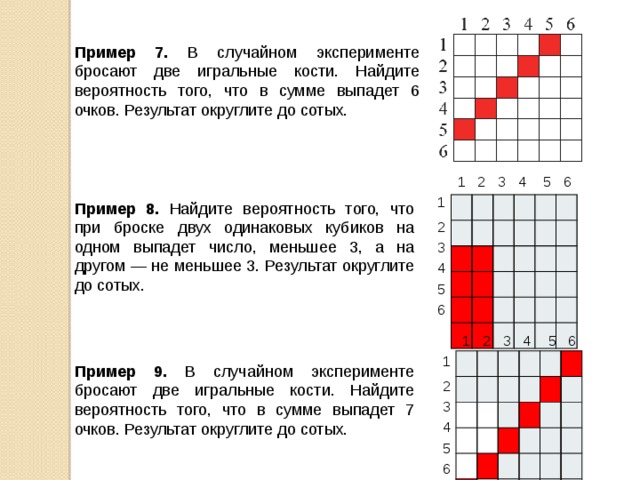
Пример 7. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 6 очков. Результат округлите до сотых.

1

2

4

5

6

3

1

Пример 8. Найдите вероятность того, что при броске двух одинаковых кубиков на одном выпадет число, меньшее 3, а на другом — не меньшее 3. Результат округлите до сотых.

2

3

4

5

6

1

2

4

5

6

3

1

Пример 9. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.

2

3

4

5

6

Пример 10. На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с вишней. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с вишней.

Пример 11. В среднем из 1000 аккумуляторов, поступивших в продажу, 7 неисправны. Найдите вероятность того, что один купленный аккумулятор окажется исправным.

Пример 12. В группе иностранных туристов 51 человек, среди них два француза. Для посещения маленького музея группу случайным образом делят на три подгруппы, одинаковые по численности. Найдите

вероятность того, что французы окажутся в одной подгруппе.

Пример 13. В кармане у Пети было 4 монеты по рублю и 2 монеты по 2 рубля. Петя, не глядя, переложил какие-то три монеты в другой карман. Найдите вероятность того, что обе двухрублевые монеты лежат в одном кармане.

Пример 14. На соревнования по метанию диска приехали 36 спортсменов, среди них 4 спортсмена из Голландии, 6 спортсменов из Испании, 5 — из Китая. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что девятым будет выступать метатель из Испании. Результат округлите до сотых.

Пример 15. Перед началом первого тура чемпионата по шахматам

участников разбивают на игровые пары случайным образом с

помощью жребия. Всего в чемпионате участвует 106 шахматистов, среди которых 22 из России, в том числе Николай Трифонов. Найдите

вероятность того, что в первом туре Николай Трифонов будет играть с

шахматистом из России.

Пример 16. В сборнике билетов по истории всего 50 билетов, в 9 из них

встречается вопрос по древней истории, а в 11 — по средневековью,

при этом ровно в 3 билетах встречаются вопросы и по древней истории, и по средневековью. Найдите вероятность того, что в случайно

выбранном билете по истории школьнику Диме не достанется вопроса ни по древней истории, ни по средневековью.

Пример 17. Научная конференция по биологии проводится в 4 дня. Всего запланировано 45 докладов: в первый день 15 докладов, остальные распределены поровну между вторым, третьим и четвёртым

днями. Порядок докладов определяется жеребьёвкой. Найдите вероятность, что доклад профессора Михайловского по позвоночным запланирован на второй день конференции. Результат округлите до сотых.

18. В кармане у Пети было 2 монеты по 5 рублей и 4 монеты по 10 рублей. Петя, не глядя, переложил какие-то 3 монеты в другой карман. Найдите вероятность того, что пятирублевые монеты лежат теперь в разных карманах.

Ответ: 0,6.

19. Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.

Ответ: 0,93.

В некоторых задачах для решения нужно использовать свойства вероятностей.

Вероятности противоположных событий связаны равенством:

Объединение (сумма) событий A и B — событие, состоящее из элементарных исходов, благоприятствующих хотя бы одному из событий A, B.

Несовместные события . Два события называются несовместными, если наступление одного из них исключает наступление другого в одном и том же опыте, т.е. эти события не могут произойти вместе в одном опыте.

Теорема о сложения вероятностей несовместных событий.

Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий Р(А + В) = Р(А) + Р(В).

Пересечение (произведение) событий A и B — событие, состоящее из элементарных исходов, благоприятствующих обоим событиям A и B.

Независимые события. События A и B называются независимыми, если наступление одного из событий не зависит от наступления другого.

Теорема об умножении вероятностей независимых событий.

Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий

Пример 1. Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,05. Покупатель в магазине выбирает одну новую ручку. Найдите вероятность того, что эта ручка пишет хорошо.

Пример 2. Имеется 2 ящика, содержащих по 10 деталей. В первом ящике 8 стандартных деталей, во втором – 7. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что обе детали окажутся стандартными.

Пример 3. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два раза промахнулся. Результат округлите до сотых.

Пример 4. В показательных выступлениях по фигурному катанию участвуют 4 девушки и 5 юношей. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что первые две выступают девушки. Результат округлите до сотых.

Пример 5. Из 20 полученных магазином компьютеров 3 оказались с дефектами. Школа купила в этом магазине 2 компьютера. Какова вероятность того, что оба компьютера не имеют дефектов? Результат округлите до сотых.

6. Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая — 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Ответ: 0,019.

7. Помещение освещается фонарём с двумя лампами. Вероятность перегорания лампы в течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.

Ответ: 0,91

8. Вероятность того, что новый электрический чайник прослужит больше года, равна 0,97. Вероятность того, что он прослужит больше двух лет, равна 0,89. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.

Ответ: 0,08.

9. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 20 пассажиров, равна 0,94. Вероятность того, что окажется меньше 15 пассажиров, равна 0,56. Найдите вероятность того, что число пассажиров будет от 15 до 19.

Ответ: 0,38.

10. Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.

Ответ: 0,52.

11. Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,4.

Ответ: 0,32.

12. Чтобы поступить в институт на специальность «Лингвистика», абитуриент должен набрать на ЕГЭ не менее 70 баллов по каждому из трёх предметов — математика, русский язык и иностранный язык. Чтобы поступить на специальность «Коммерция», нужно набрать не менее 70 баллов по каждому из трёх предметов — математика, русский язык и обществознание. Вероятность того, что абитуриент З. получит не менее 70 баллов по математике, равна 0,6, по русскому языку — 0,8, по иностранному языку — 0,7 и по обществознанию — 0,5.

Найдите вероятность того, что З. сможет поступить хотя бы на одну из двух упомянутых специальностей.

Ответ: 0,408.

13. Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная батарейка будет забракована системой контроля.

Ответ: 0,0296

14. На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Результат округлите до сотых.

Ответ: 0,98.

15. По отзывам покупателей Иван Иванович оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,8. Вероятность того, что этот товар доставят из магазина Б, равна 0,9. Иван Иванович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар.

Ответ: 0,02.

16. В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.

Ответ: 0,392

17. Всем пациентам с подозрением на гепатит делают анализ крови. Если анализ выявляет гепатит, то результат анализа называется  положительным . У больных гепатитом пациентов анализ даёт положительный результат с вероятностью 0,9. Если пациент не болен гепатитом, то анализ может дать ложный положительный результат с вероятностью 0,01. Известно, что 5% пациентов, поступающих с подозрением на гепатит, действительно больны гепатитом. Найдите вероятность того, что результат анализа у пациента, поступившего в клинику с подозрением на гепатит, будет положительным.

Ответ: 0,0545.

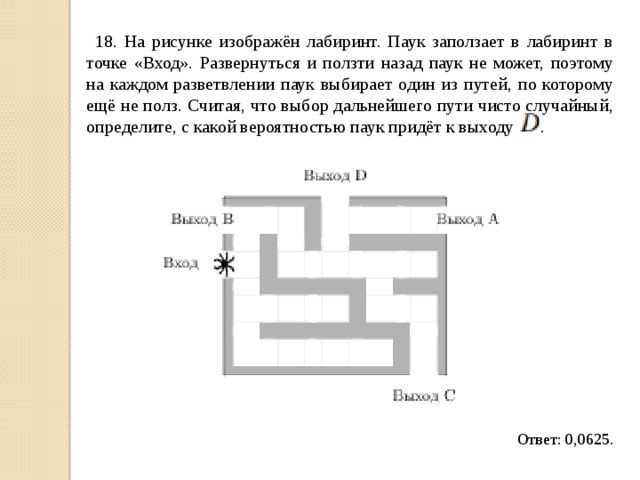
18. На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу   .

Ответ: 0,0625.

19. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.

Ответ: 0,75.

20. В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.

Ответ: 0,9975.

21. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах.

Ответ: 0,52.

22. Стрелок стреляет по мишени один раз. В случае промаха стрелок делает второй выстрел по той же мишени. Вероятность попасть в мишень при одном выстреле равна 0,7. Найдите вероятность того, что мишень будет поражена (либо первым, либо вторым выстрелом).

Ответ: 0,91.

23. При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем — 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?

Ответ: 5.