Векторы в пространстве

Зачет по теме:

«Векторы в пространстве»

I вариант

Теоретическая часть

1. Определение вектора.

2. Определение длины ненулевого вектора.

3. Какие векторы называются компланарными?

4. Как вычисляются координаты середины отрезка?

5. Определение скалярного произведения двух векторов.

Практическая часть

1. Упростить: .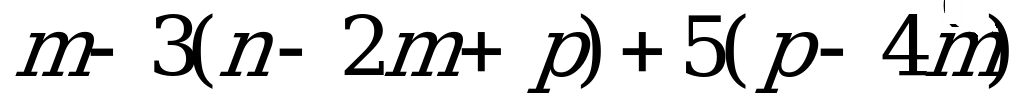

2. Даны векторы: .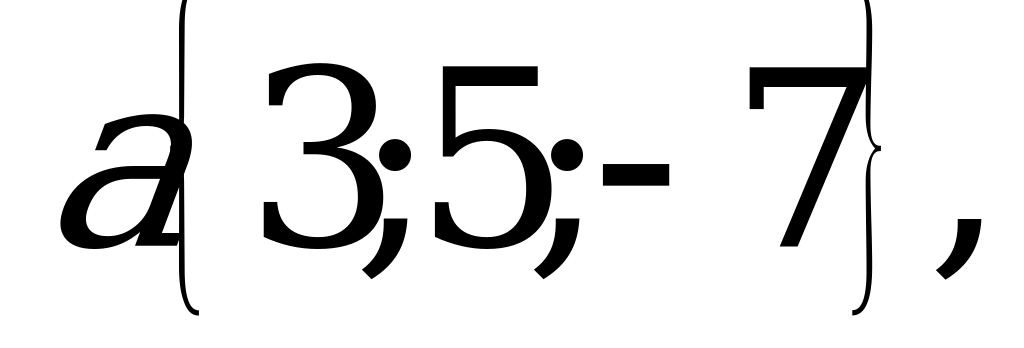

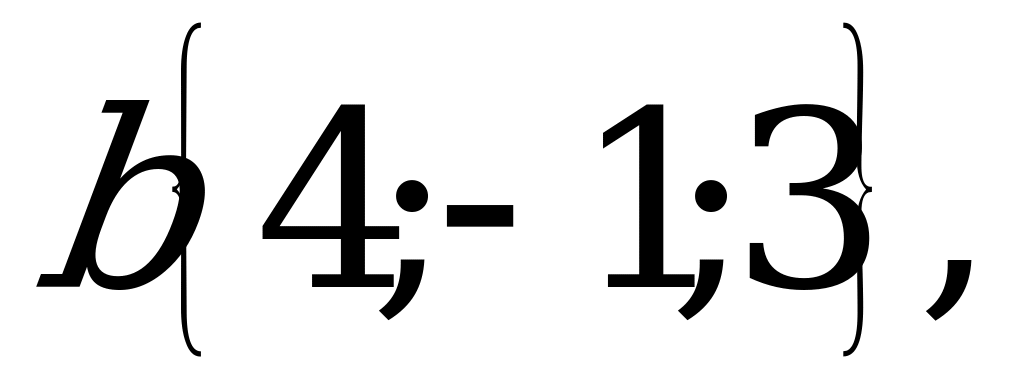
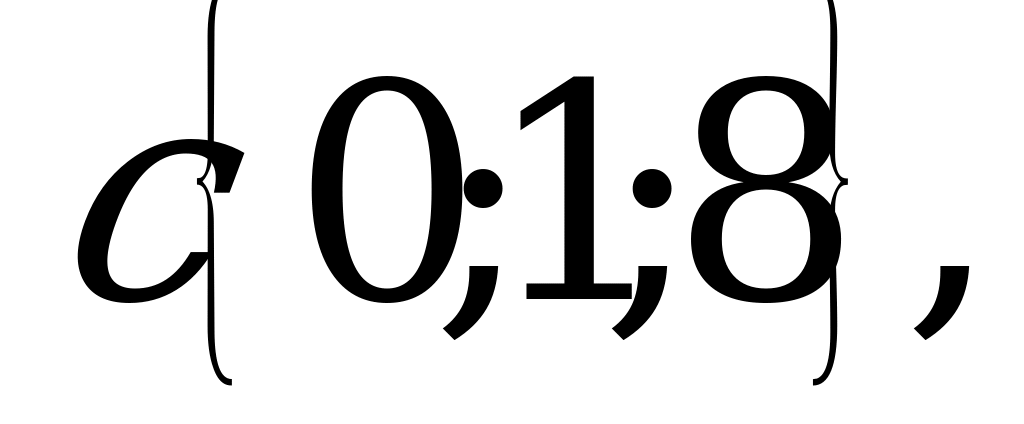
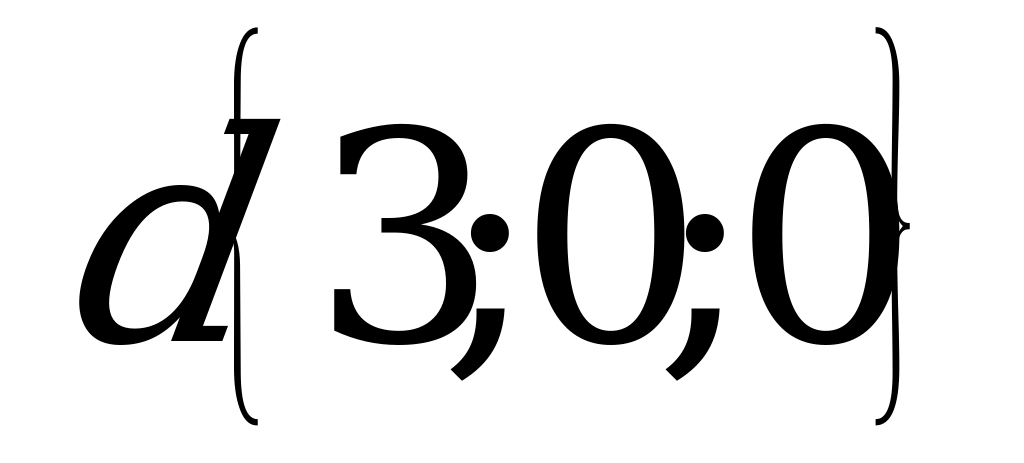а) разложите их по координатным векторам;

б) найдите координаты следующих векторов: .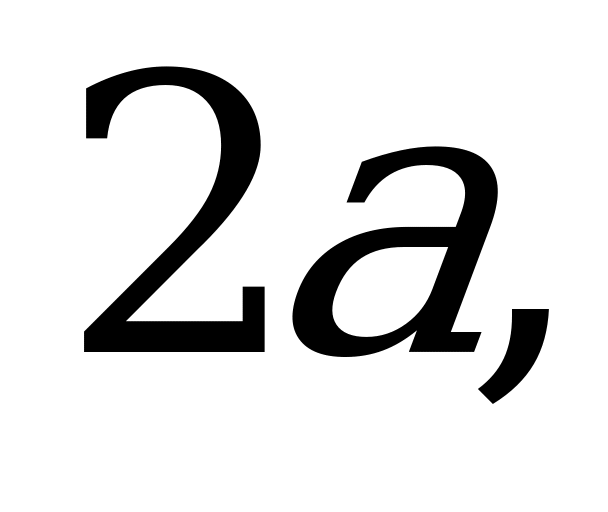

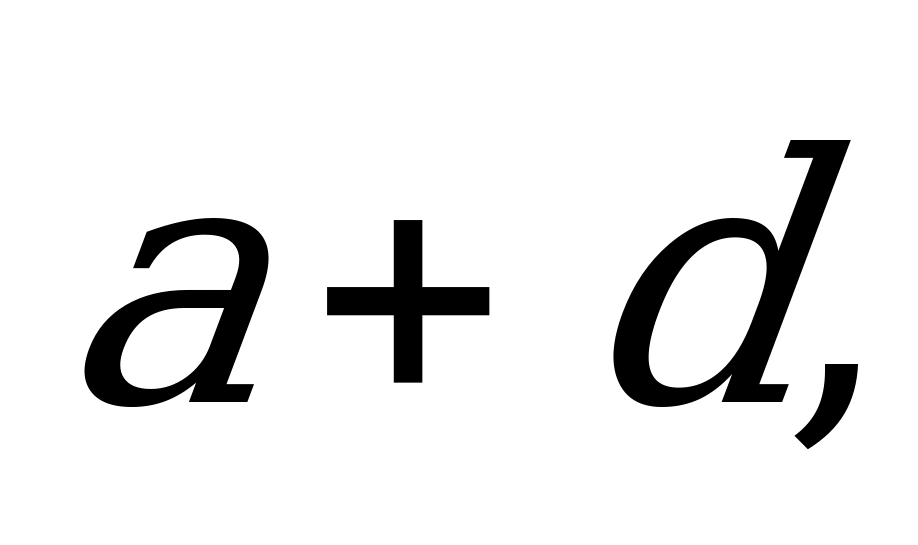
3. Дано: А(2;-1;0), В(-3;2;1), С(1;1;4). Найдите:

а) Найдите D(x;y;z), если AB=CD;

б) определите координаты точки М, если известно, что М – середина CD.

4. Дано: , , , , .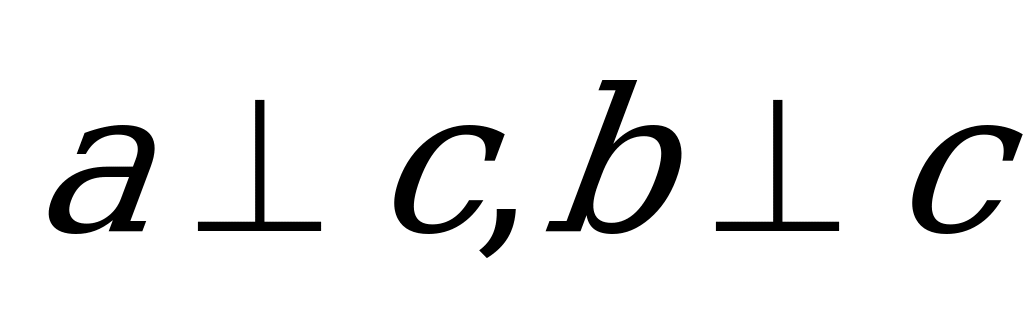

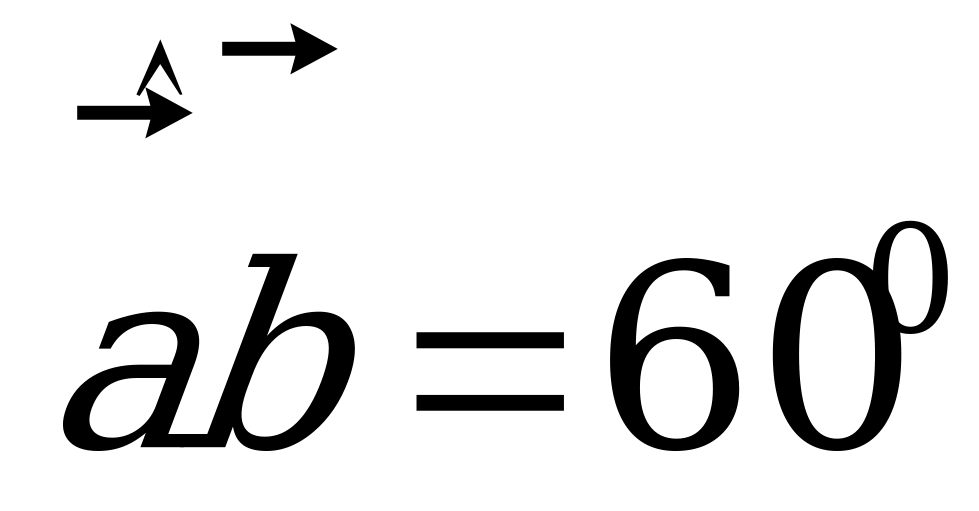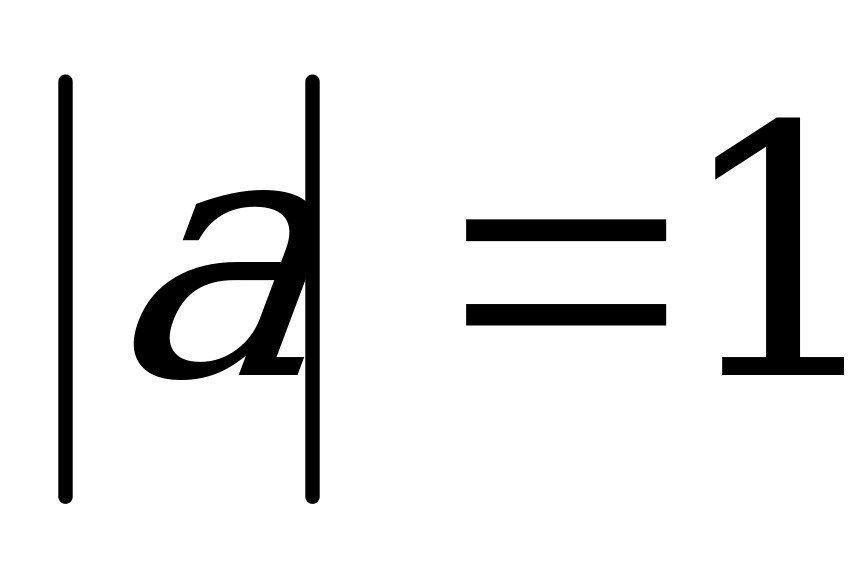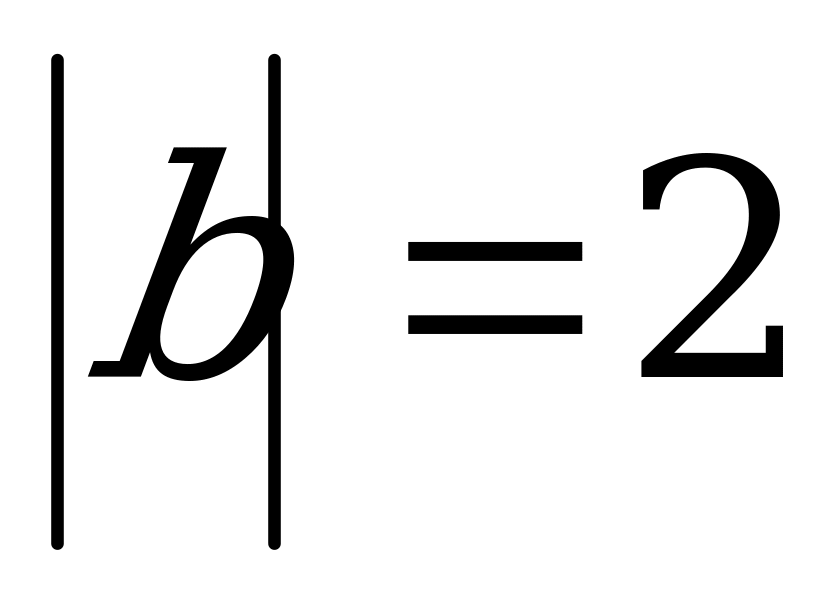Найти скалярное произведение: .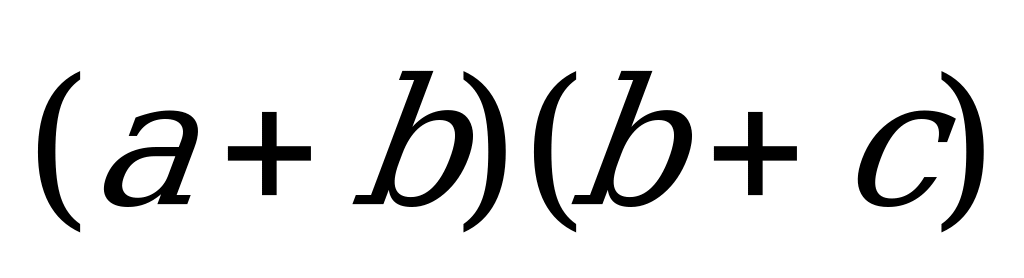

5. Дано: А(3;5;4), B(4;6;5), C (6;-2;1), D(5;-3;0). Доказать, что ABCD – параллелограмм.

Оценка «3» - теоретическая часть + задания №1-3 практической части

Оценка «4» - теоретическая часть + задания №1-4 практической части

Оценка «5» - теоретическая часть + задания №1-5 практической части

Зачет по теме:

«Векторы в пространстве»

II вариант

Теоретическая часть

1. Определение вектора.

2. Как разложить вектор по координатным векторам?

3. Какие векторы называются равными?

4. Как вычислить расстояние между двумя точками, если известны их координаты?

5. Как вычислить угол между прямыми, если известны координаты направляющих векторов этих прямых?

Практическая часть

1. Упростить: .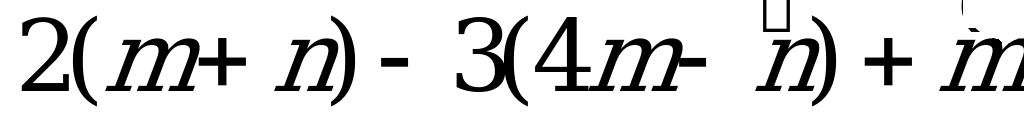

2. Даны векторы: .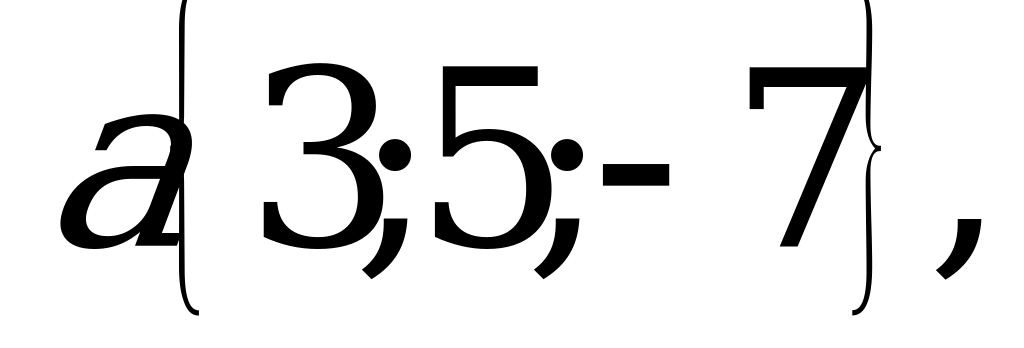

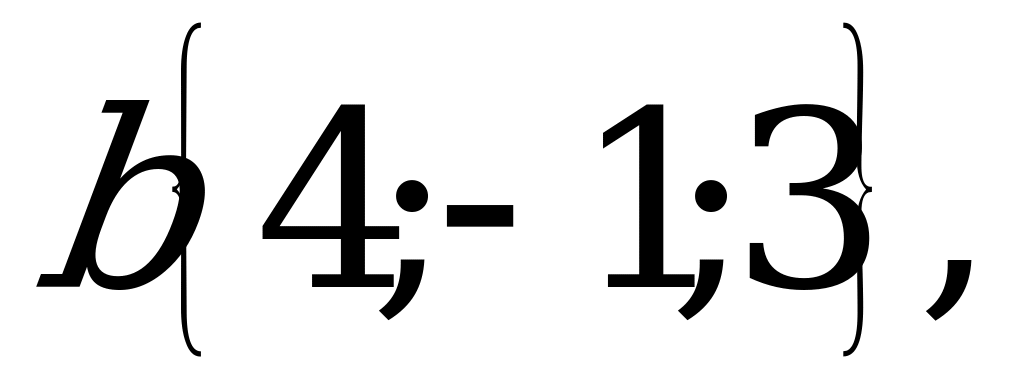
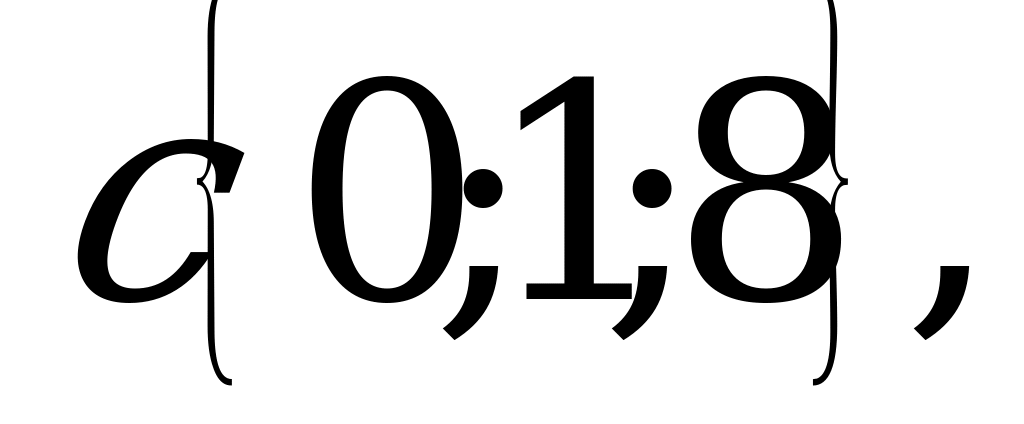
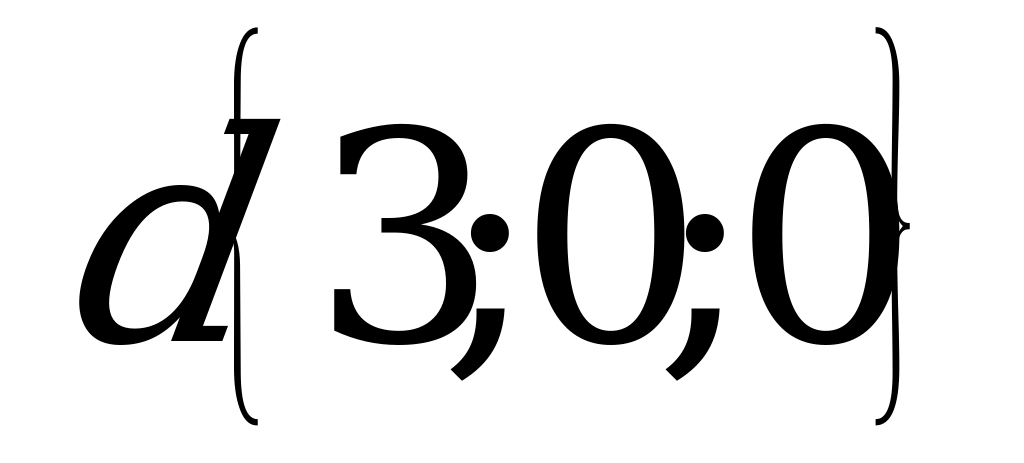а) разложите их по координатным векторам;

б) найдите координаты следующих векторов: .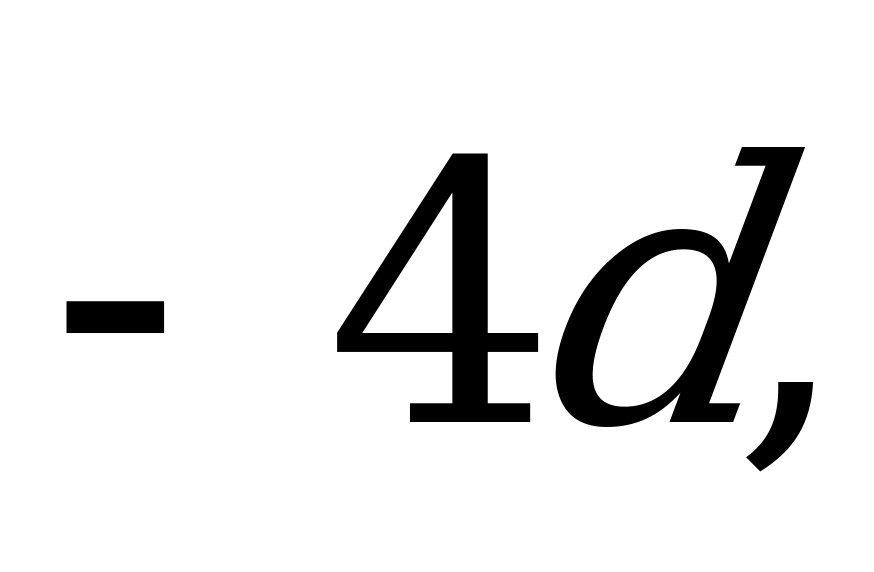

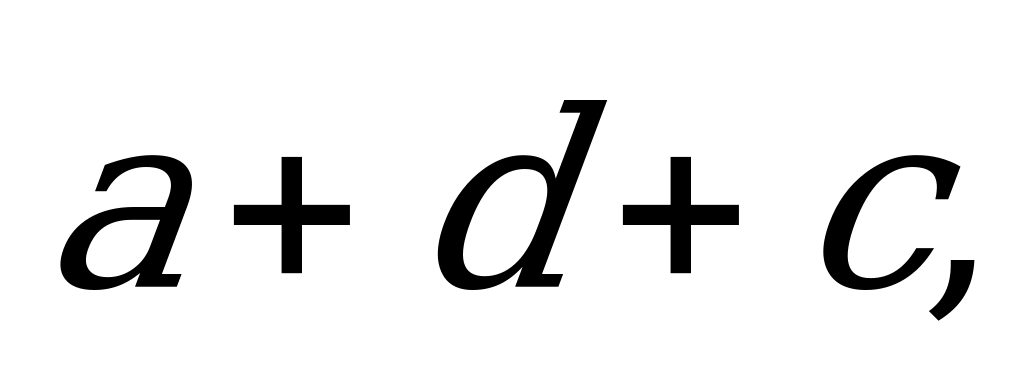
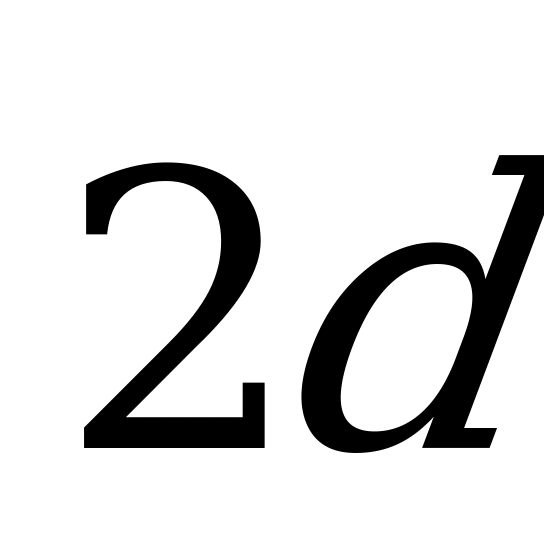3. Дано: А(2;-1;0), В(-3;2;1), С(1;1;4). Найдите:

а) Найдите D(x;y;z), если AC=DB;

б) определите координаты точки М, если известно, что М – середина DB.

4. Дано: , , , , .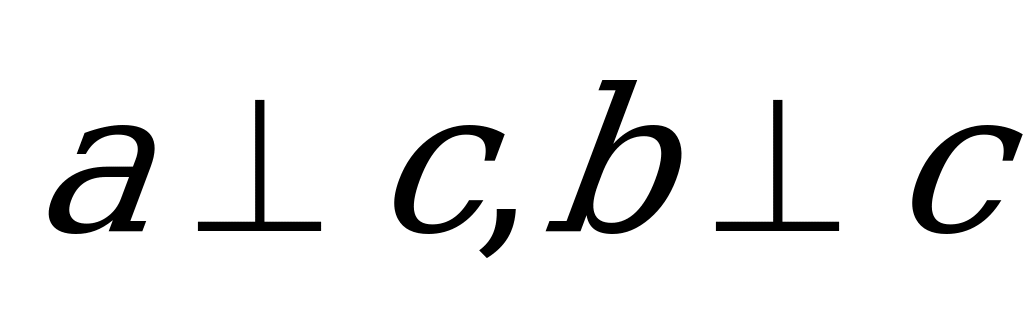

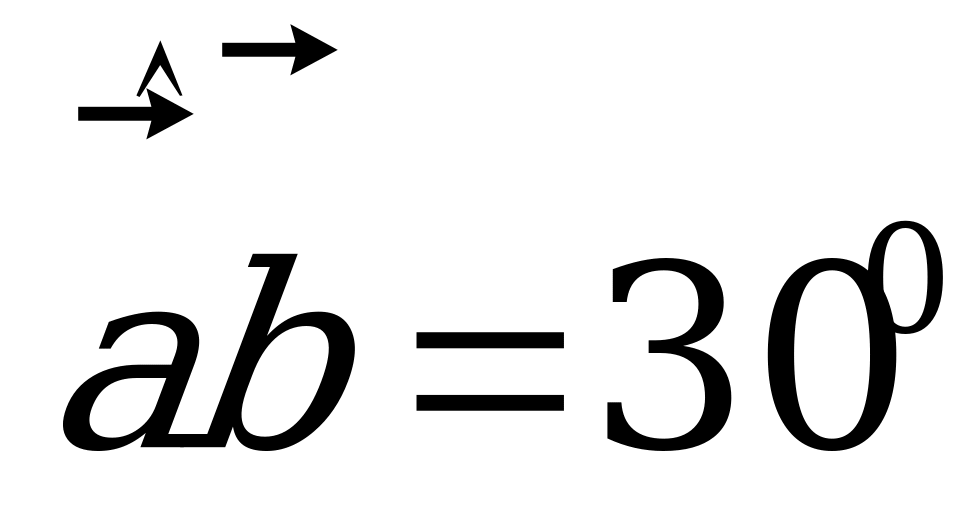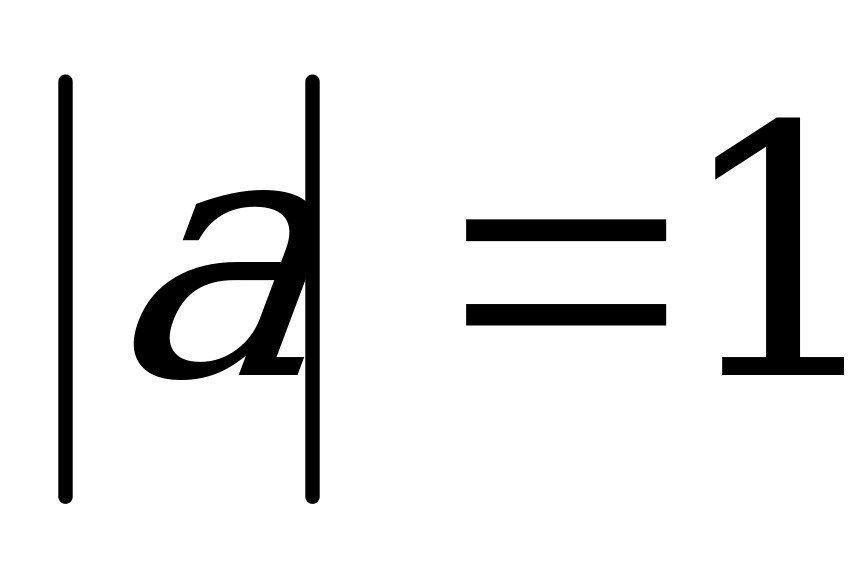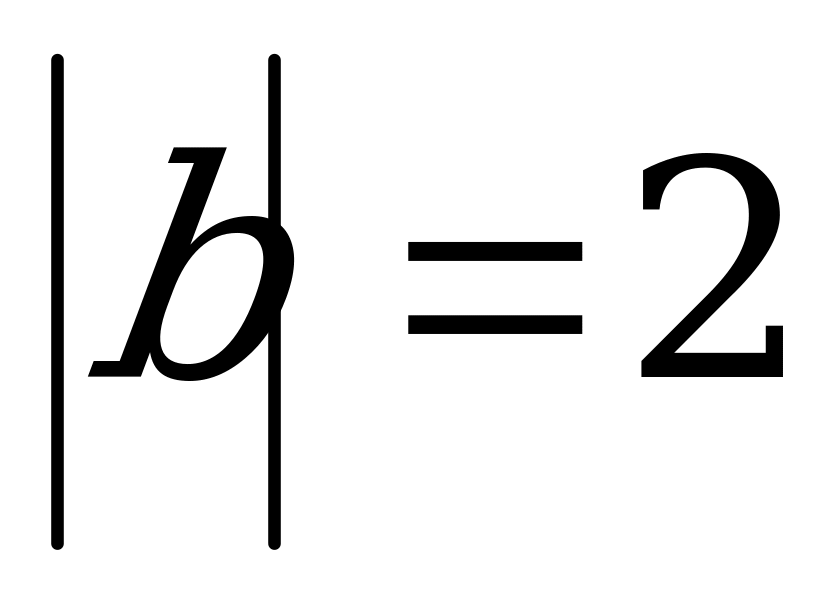Найти скалярное произведение: .

5. Дано: А(3;5;4), B(4;6;5), C (6;-2;1), D(5;-3;0). Доказать, что ABCD – параллелограмм.

Оценка «3» - теоретическая часть + задания №1-3 практической части

Оценка «4» - теоретическая часть + задания №1-4 практической части

Оценка «5» - теоретическая часть + задания №1-5 практической части