Входная контрольная работа по математике 11 класс
Цель: выявление типичных пробелов в знаниях обучающихся с целью организации работы по их ликвидации, систематизация и обобщение знаний обучающихся, а также в целях подготовки к государственной итоговой аттестации на основе системных мониторинговых исследований.
Оценивание работы:
Каждое задание первой части оценивается одним баллом. Во второй части задание – два балла. Вся работа оценивается 12 баллами.
ПЕРЕВОД БАЛЛОВ В ОТМЕТКУ:
| БАЛЛ | 0 - 4 | 5- 7 | 8 - 10 | 10– 12 |
| ОТМЕТКА | 2 | 3 |
4 | 5 |
1 вариант
В1. В общежитии института в каждой комнате можно поселить четырёх человек. Какое наименьшее количество комнат необходимо для поселения 83 иногородних студентов?
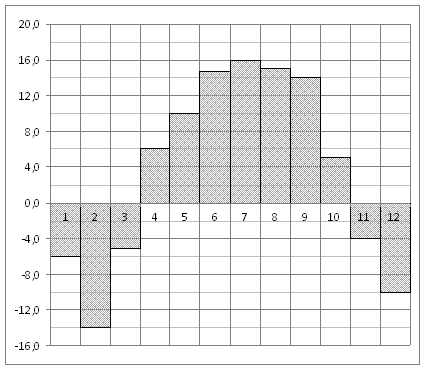
В2. На диаграмме показана среднемесячная температура воздуха в Нижнем Новгороде за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали – температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру в 1994 году.
В3. Решите уравнение: а) log ¼ (3х + 22) = -3; б) 27 – х = 32; в) 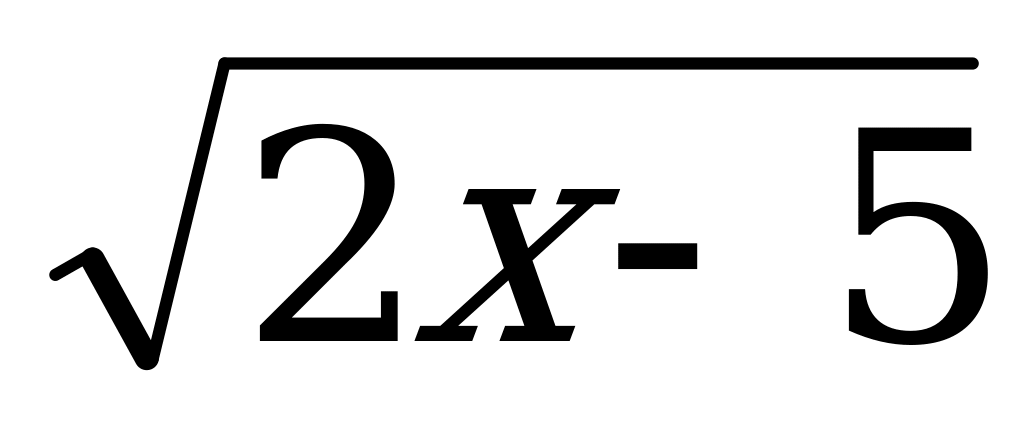 = 4.
= 4.
В4. В треугольнике АВС угол С = 90°, АВ = 25, АС = 20. Найти sin А.
В5. Найдите значение выражения: а) log 5 25 – log 5 0,2; б) 23,5 ∙35,5 : 64,5; в) 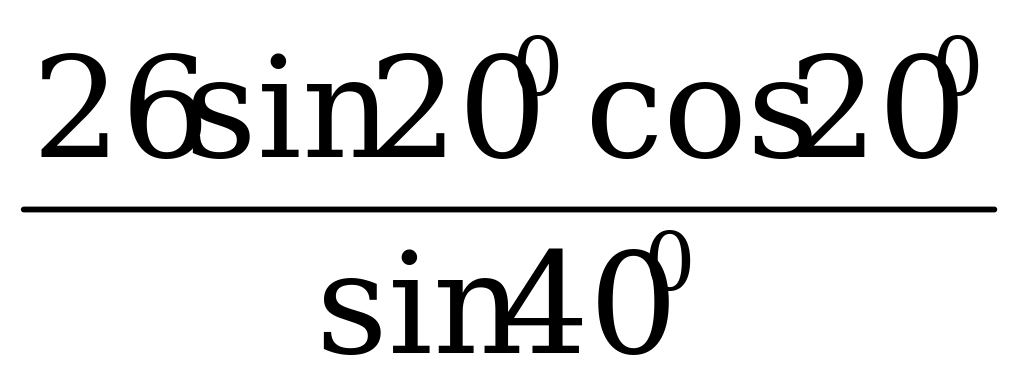 .
.
В6. Найдите sin α, если cos α = 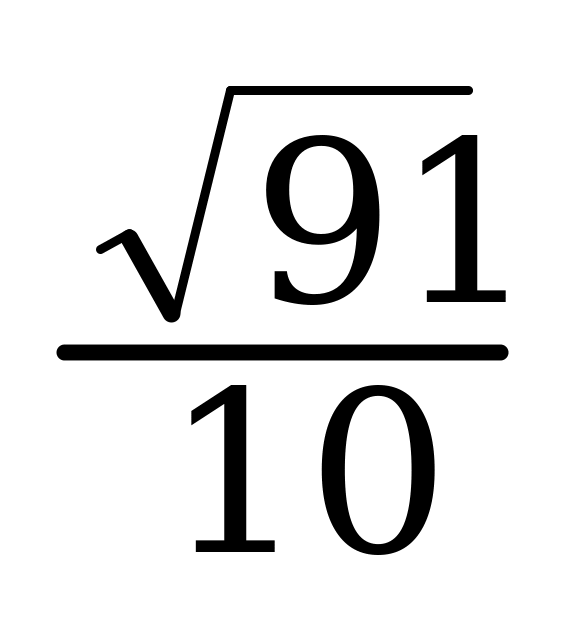 и α € (0; π).
и α € (0; π).
В 7. В вагоне электрички из 20 пассажиров 3 – безбилетники. Контролёр проверил билет у одного из пассажиров наудачу. Найдите вероятность того, что этот пассажир не имеет билета.
7. В вагоне электрички из 20 пассажиров 3 – безбилетники. Контролёр проверил билет у одного из пассажиров наудачу. Найдите вероятность того, что этот пассажир не имеет билета.
В8. Найдите квадрат расстояния между вершинами С и А1 прямоугольного параллелепипеда АВСДА1В1С1Д1 для которого АВ = 5, АД = 4, АА1 = 3.
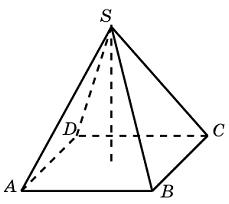
В9. В правильной четырёхугольной пирамиде SАВСД точка О – центр основания, S – вершина, SВ = 13, АС = 24. Найдите длину отрезка SО.
В10. Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной L км c постоянным ускорением a км/ч2, вычисляется по формуле v =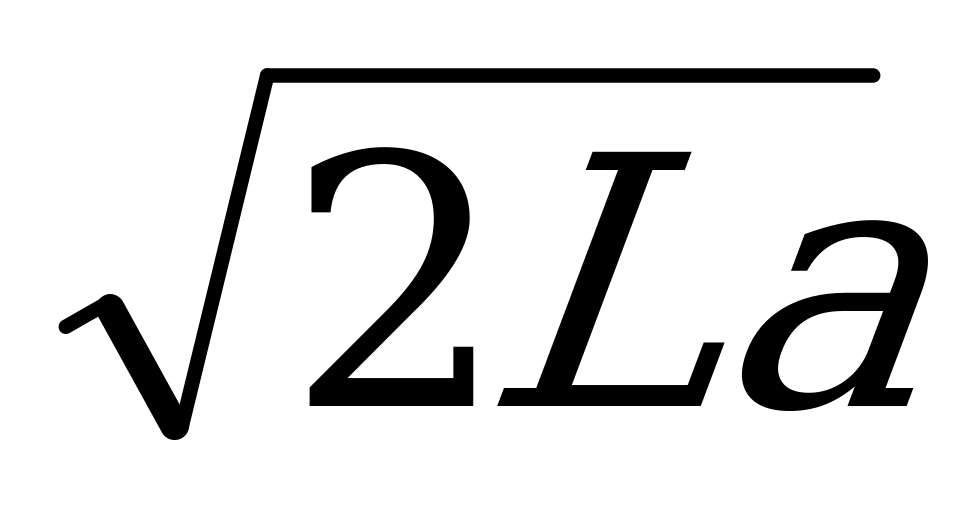 . Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав один км, приобрести скорость не менее 100 км/ч.
. Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав один км, приобрести скорость не менее 100 км/ч.
С1. а) Решите уравнение log 2 (cosx + sin2x + 8) = 3.
б) Найдите все корни этого уравнения, принадлежащие отрезку 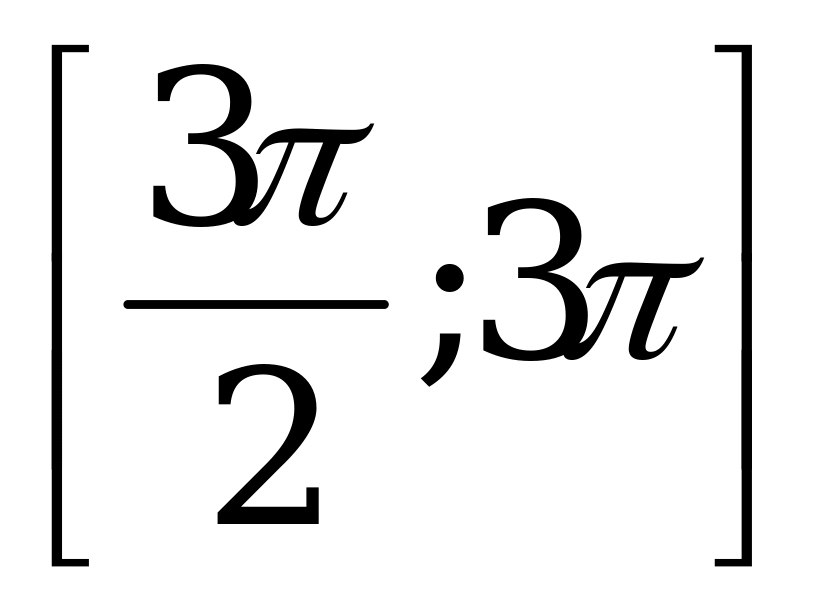 .
.
Входной контроль, 11 класс, 2 вариант
В1. Призёрами городской олимпиады по математике стало 48 учеников, что составляет 12% от числа участников. Сколько человек участвовало в олимпиаде?
В2. На рисунке жирными точками показана цена золота на момент закрытия биржевых торгов во все рабочие дни с 5 по 28 марта 1996 года. По горизонтали указываются числа, по вертикали – цена унции золота в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа цена золота на момент закрытия торгов была наименьшей за данный период.

В3. Решите уравнение: а) log 1/2 (2х – 5) = -2; б) 39 – х = 81; в) 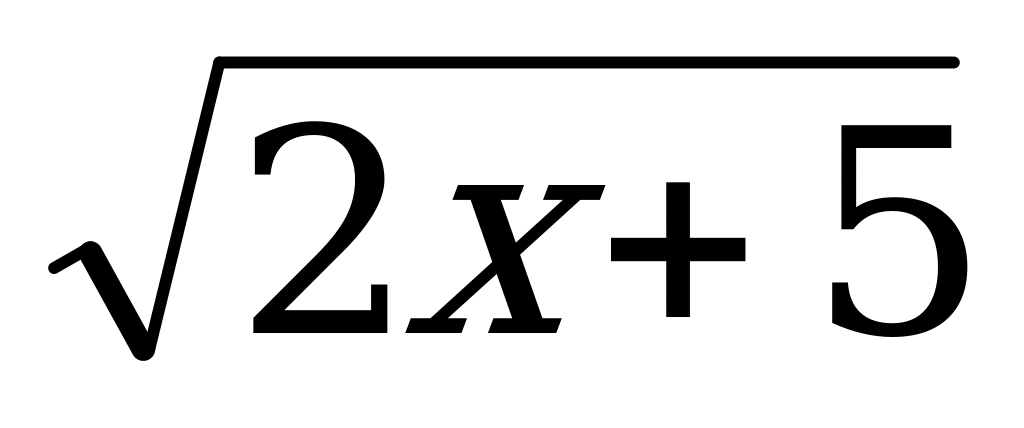 = 7.
= 7.
В4. В треугольнике АВС угол С = 90°, АС = 24, ВС = 7. Найти cos А.
В5. Найдите значение выражения: а) log 3 8,1 + log 310;б) 48 ∙1110 : 448; в) 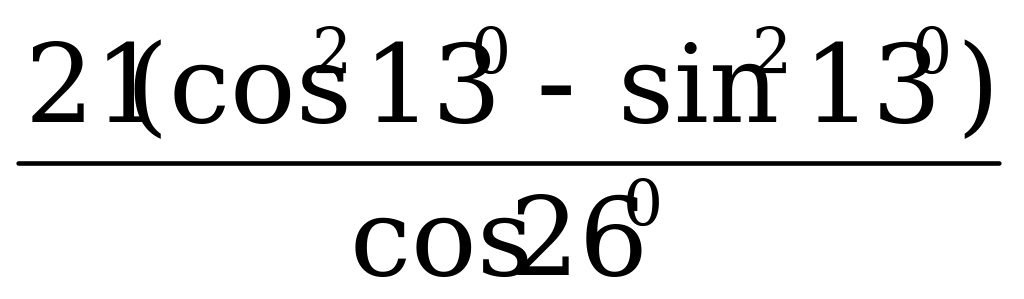 .
.
В6. Найдите cos α, если sin α = - 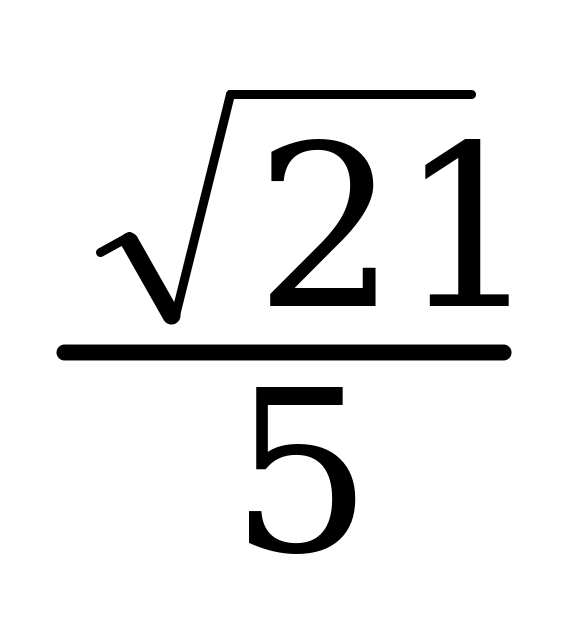 и α € ( π/2; 3π/2).
и α € ( π/2; 3π/2).
В 7. У Петра много тетрадей, часть из них в линию, остальные в клеточку. При этом из 15 тетрадей в среднем 9 в клеточку. Найдите вероятность того, что наугад взятая тетрадь – в линию.
7. У Петра много тетрадей, часть из них в линию, остальные в клеточку. При этом из 15 тетрадей в среднем 9 в клеточку. Найдите вероятность того, что наугад взятая тетрадь – в линию.
В8. В прямоугольном параллелепипеде АВСДА1В1С1Д1 известно, что ВД1 = 3, СД = 2, АД = 2. Найдите длину ребра АА1.
В9. В правильной четырёхугольной пирамиде SАВСД точка О – центр основания, S – вершина, SО = 8, ВД = 30. Найдите боковое ребро SС.

В10. Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной L км c постоянным ускорением a км/ч2, вычисляется по формуле v =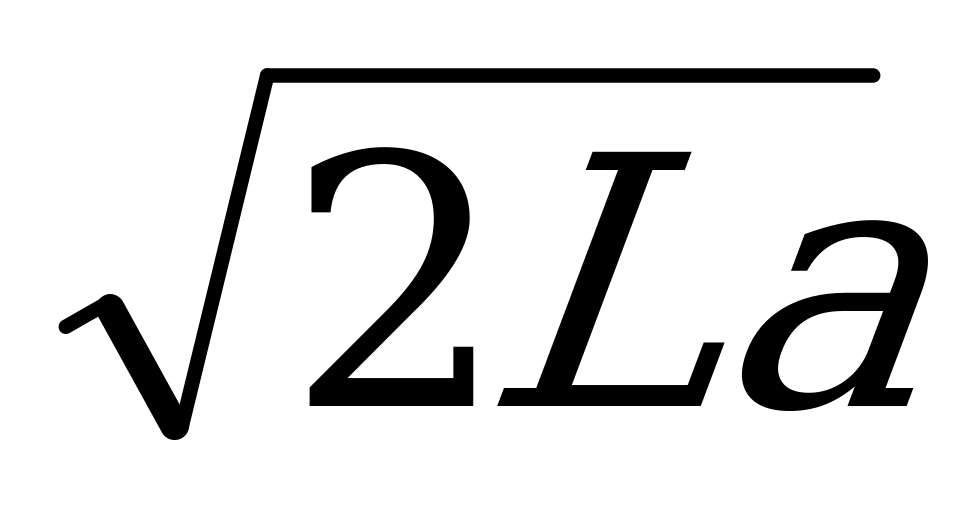 . Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав один км, приобрести скорость не менее 110 км/ч.
. Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав один км, приобрести скорость не менее 110 км/ч.
С1. а) Решите уравнение log 4 (sinx + sin2x + 16) = 2.
б) Найдите все корни этого уравнения, принадлежащие отрезку 
Входной контроль, 11 класс, 3 вариант
В1. Стоимость проезда в маршрутном такси составляет 20 руб. Какое наибольшее число поездок можно будет совершить в этом маршрутном такси на 150 руб., если цена проезда снизится на 10%?
В2. На диаграмме показана среднемесячная температура воздуха в Нижнем Новгороде за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали – температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру в 1994 году.

В3. Решите уравнение: а) log ¼ (2х - 10) = - 4; б) 57 + х = 125 ; в) 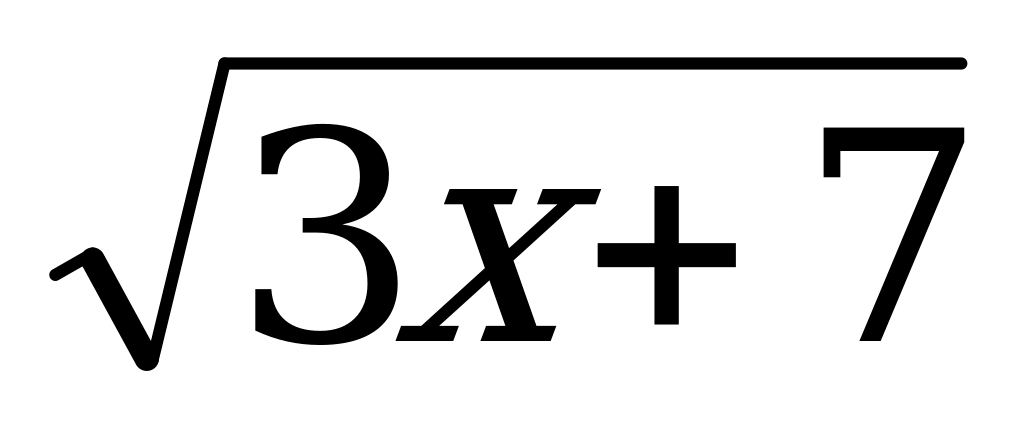 = 5.
= 5.
В4. В треугольнике АВС угол С = 90°, АВ = 13, АС = 12. Найти tg В.
В5. Найдите значение выражения: а) log 5 6 – log 5 1,2; б) 56,5 ∙75,5 : 354,5; в)  .
.
В6. Найдите sin α, если cos α = - 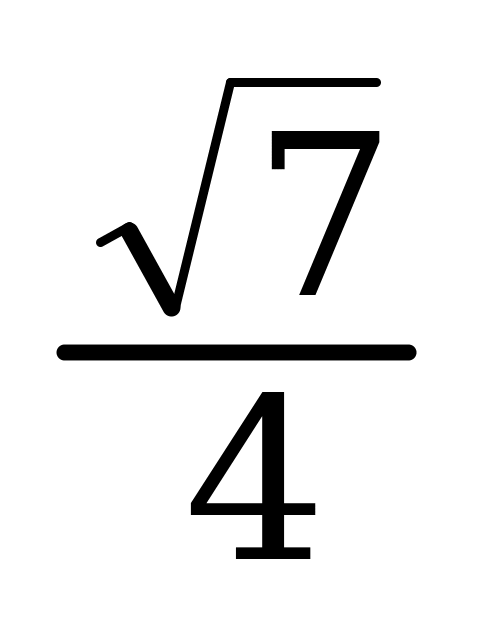 и α € ( π/2; π).
и α € ( π/2; π).
В 7. В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по неравенствам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам.
7. В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по неравенствам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам.
В8. Найдите длину диагонали АС1 прямоугольного параллелепипеда АВСДА1В1С1Д1 для которого АВ = 14, АД = 14, АА1 = 7.
В9. В правильной четырёхугольной пирамиде SАВСД точка О – центр основания, S – вершина, SВ = 25, АС = 14. Найдите длину отрезка SО.

В10. Расстояние от наблюдателя, находящегося на небольшой высоте h километров над землeй до наблюдаемой им линии горизонта вычисляется по формуле 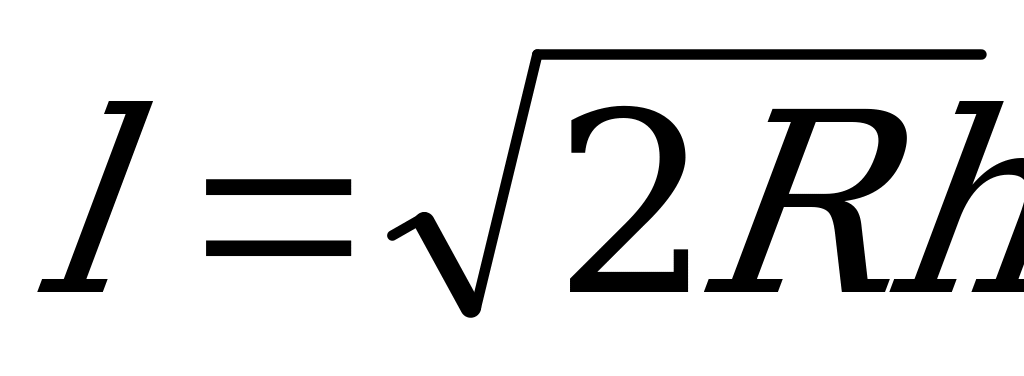 , где R = 6400 (км) − радиус Земли. С какой высоты горизонт виден на расстоянии 8 километров? Ответ выразите в километрах.
, где R = 6400 (км) − радиус Земли. С какой высоты горизонт виден на расстоянии 8 километров? Ответ выразите в километрах.
С1. а) Решите уравнение log 3 (cos(π – x) + sin2x + 9) = 2.
б) Найдите все корни этого уравнения, принадлежащие отрезку 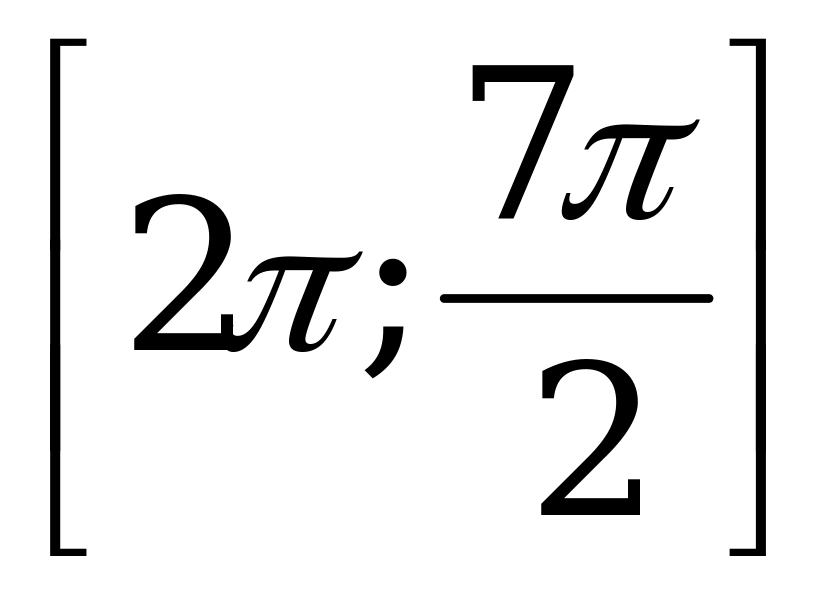
Входной контроль, 11 класс, 4 вариант
В1. Каждый день во время конференции расходуется 70 пакетиков чая. Конференция длится 6 дней. Чай продается в пачках по 50 пакетиков. Сколько пачек нужно купить на все дни конференции?
В2. На рисунке жирными точками показана цена золота на момент закрытия биржевых торгов во все рабочие дни с 5 по 28 марта 1996 года. По горизонтали указываются числа, по вертикали – цена унции золота в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа цена золота на момент закрытия торгов была наибольшей за данный период.

В3. Решите уравнение: а) log 1/2 (2х + 8) = -5; б) 79 + х = 343; в) 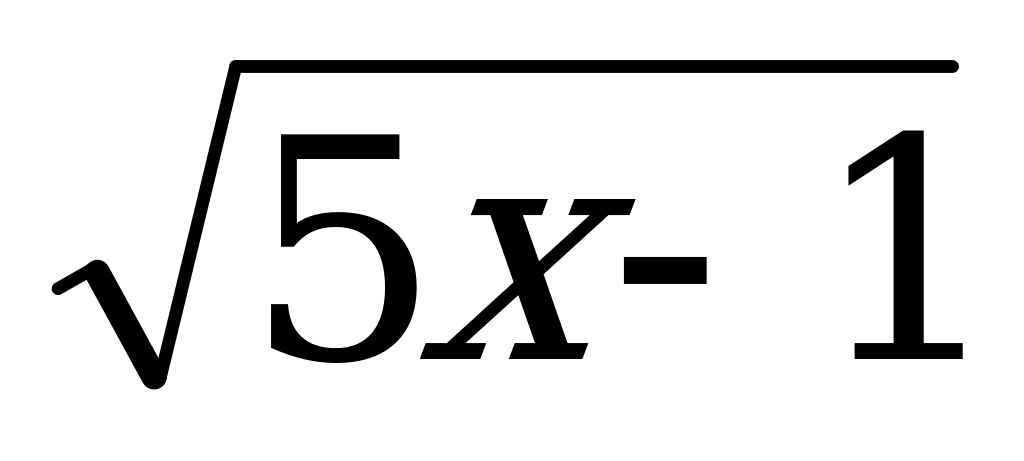 = 9.
= 9.
В4. В треугольнике АВС угол С = 90°, АВ = 15, ВС = 9. Найти cos А.
В5. Найдите значение выражения: а) log 3 0,27 + log 3100 ;б) 138 ∙210 : 267; в) 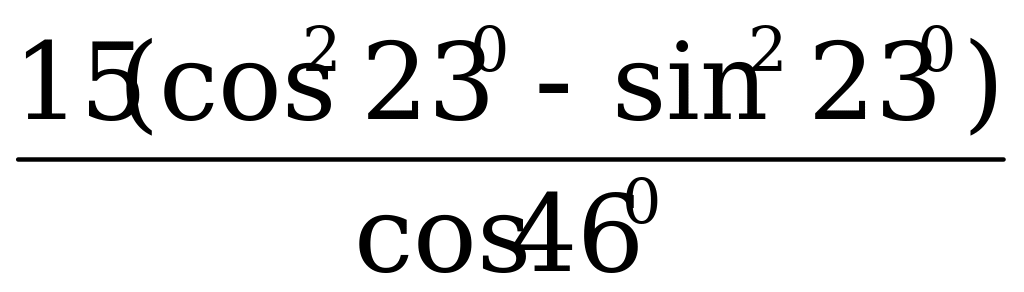 .
.
В6. Найдите cos α, если sin α = -  и α € (3π/2; 2π).
и α € (3π/2; 2π).
В 7. В сборнике билетов по биологии всего 55 билетов, в 11 из них встречается вопрос по ботанике. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по ботанике.
7. В сборнике билетов по биологии всего 55 билетов, в 11 из них встречается вопрос по ботанике. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по ботанике.
В8. В прямоугольном параллелепипеде АВСДА1В1С1Д1 известно, что ВД1 = 5, СД = 3, АД = √7. Найдите длину ребра АА1.
В9. В правильной четырёхугольной пирамиде SАВСД точка О – центр основания, S – вершина, SО = 12, ВД = 18. Найдите боковое ребро SС.

В10. Расстояние от наблюдателя, находящегося на небольшой высоте h километров над землeй до наблюдаемой им линии горизонта вычисляется по формуле 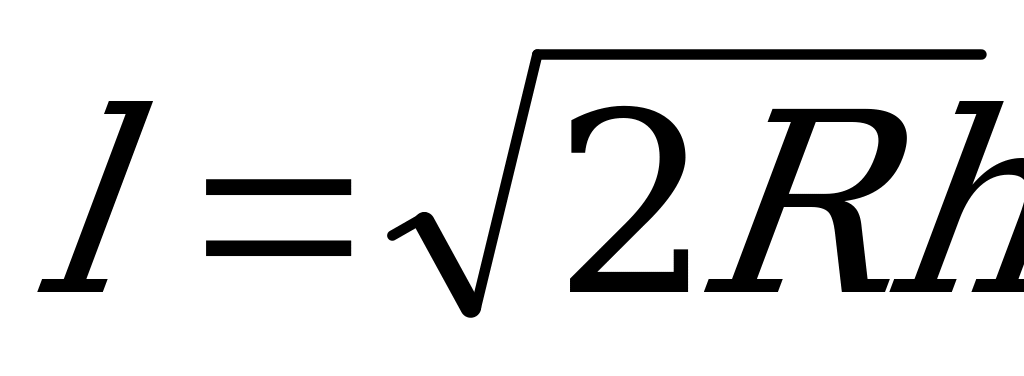 , где R = 6400 (км) − радиус Земли. С какой высоты горизонт виден на расстоянии 4 километра? Ответ выразите в километрах.
, где R = 6400 (км) − радиус Земли. С какой высоты горизонт виден на расстоянии 4 километра? Ответ выразите в километрах.
С1. а) Решите уравнение lg (cos2x - cosx + 1) = 0. б) Найдите все корни этого уравнения, принадлежащие отрезку 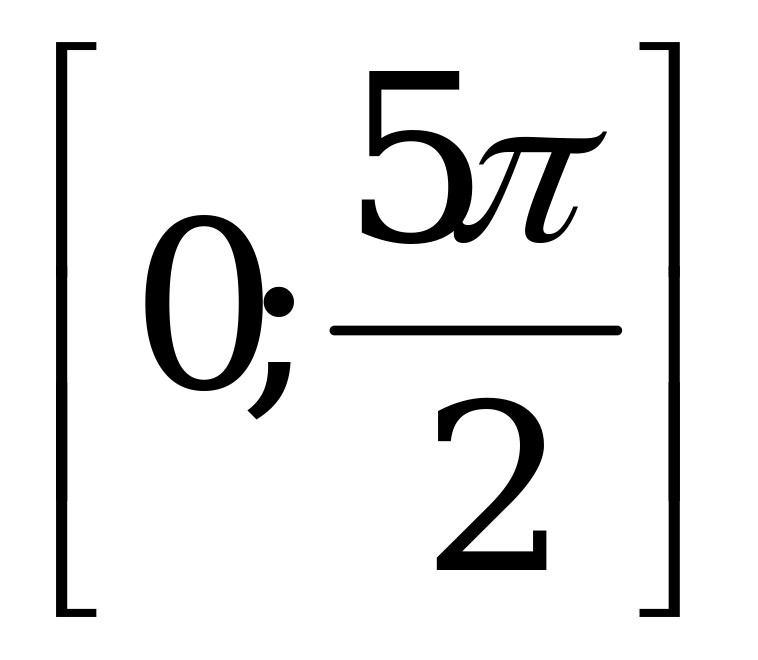
Ответы
|
| 1 вариант | 2 вариант |
| В1. | 21 | 400 |
| В2. | -14 | 6 |
| В3а. | 14 | 4,5 |
| В3б. | 2 | 5 |
| В3в. | 10,5 | 22 |
| В4. | 0,6 | 0,96 |
| В5а. | 3 | 4 |
| В5б. | 1,5 | 121 |
| В5в. | 13 | 21 |
| В6. | 0,3 | -0,4 |
| В7. | 0,15 | 0,4 |
| В8. | 50 | 1 |
| В9. | 5 | 17 |
| В10. | 5000 | 6050 |
| С1а. | 
| 
|
| С1б. | 
| 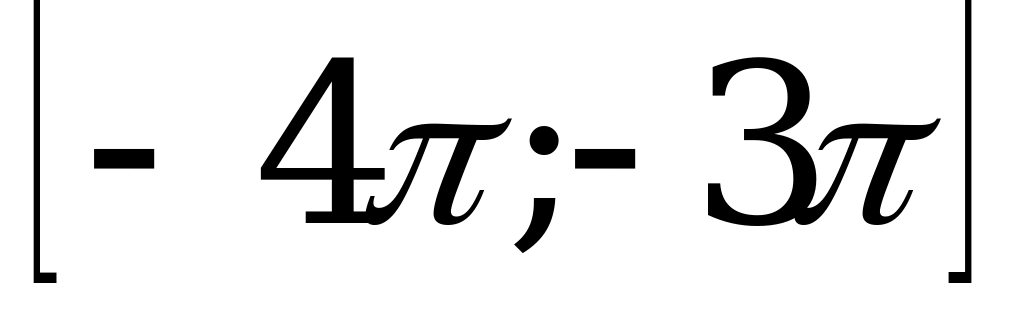
|
Ответы
|
| 3 вариант | 4 вариант |
| В1. | 8 | 9 |
| В2. | 16 | 26 |
| В3а. | 133 | 12 |
| В3б. | - 4 | - 6 |
| В3в. | 6 | 16 ,4 |
| В4. | 2,4 | 0,8 |
| В5а. | 1 | 3 |
| В5б. | 175 | 104 |
| В5в. | 24 | 15 |
| В6. | 0,75 | 0,25 |
| В7. | 0,6 | 0,2 |
| В8. | 21 | 3 |
| В9. | 24 | 15 |
| В10. | 0,005 | 0,00125 |
| С1а. | 
| 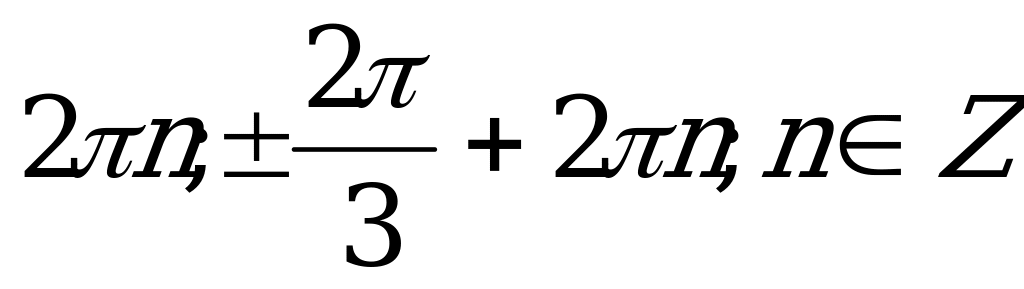
|
| С1б. | 
| 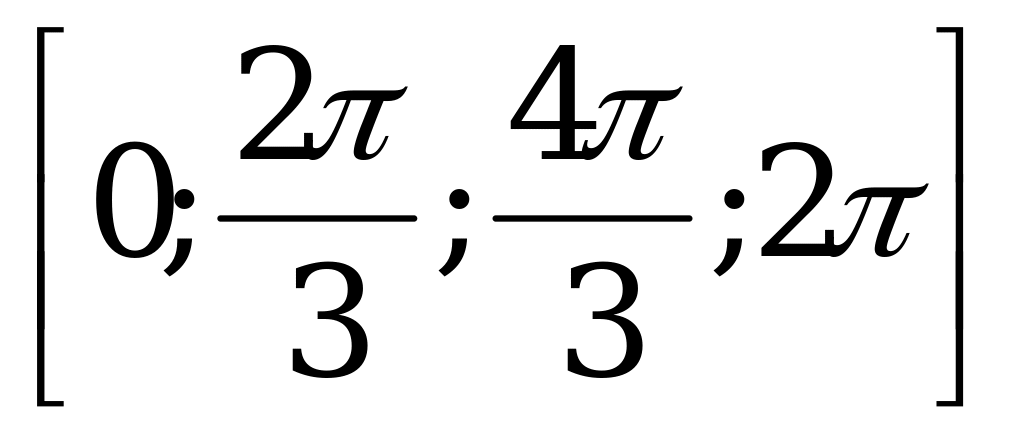
|








 7. В вагоне электрички из 20 пассажиров 3 – безбилетники. Контролёр проверил билет у одного из пассажиров наудачу. Найдите вероятность того, что этот пассажир не имеет билета.
7. В вагоне электрички из 20 пассажиров 3 – безбилетники. Контролёр проверил билет у одного из пассажиров наудачу. Найдите вероятность того, что этот пассажир не имеет билета.











