-
Влияние вычислительных навыков на развитие младших школьников.
Формирование навыков устного счёта играет важную роль в начальной школе и является одной из основных задач начального курса обучения математике. В первые годы обучения закладываются основные приемы устных вычислений, которые активизируют мыслительную деятельность, развивают у детей память, речь, способность воспринимать на слух сказанное, повышают внимание и быстроту реакции.
Несмотря на нынешнее обучение компьютерных технологий и повышением компьютерной грамотности учеников, полноценно усвоить школьную программу большинству учеников трудно. Причин много, одна из них - слаборазвитые вычислительные умения и отсутствие навыков устного счета у большинства учащихся.
Если обратиться к истории можно заметить, что и в прошлые века устный счет был одним из главных компонентов урока. На уроке математики устному счету уделялось большое внимание. В настоящее время учащиеся пользуются калькуляторами и компьютерами. Кажется, что отпала необходимости в отработке навыков учащихся устного счета. Но это ошибочное мнение.
Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение. По его собственным словам, он научился считать раньше, чем говорить. Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав. В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.
Современное российское образование участвует в подготовке новой формации людей, которые органично вольются во всемирное сообщество, оказавшееся в самом центре проблем, имеющих непосредственное отношение к развитию личности и общества. Поэтому одной из задач, доминирующей в создании более человечного и справедливого мира, является возможность дать проявить всем без исключения обучающимся свои таланты и творческий потенциал.
Решение такой задачи сегодня является предметом забот учреждений основного и дополнительного образования, обеспечивающих развитие индивидуальных способностей у детей и воспитательный процесс.
Одним из современных направлений в дополнительном образовании является ментальная арифметика. Это одна из самых популярных и перспективных методик развития умственных способностей детей.
Первая программа по ментальной арифметике в образовательных целях была запущена в Азии в 1993 г. И вот уже более двадцати пяти лет ментальная арифметика используется при обучении детей от 4 до 12 лет в 57 странах мира. Наиболее успешно она внедрена в школах Японии, Китая и Малайзии, где в корпорациях при приеме на работу нового сотрудника проходит тестирование его на предмет умения считать на специальных счетах и уровня сложности осуществляемых им вычислений. При правильном профессиональном подходе к обучению ментальной арифметике и закреплению знаний дети младшего школьного возраста демонстрируют феноменальные навыки выполнения в уме арифметических действий с двух-, трех-, четырехзначными числами.
Главными целями методики ментальной арифметики являются: умение сосредоточиться на поставленных задачах и концентрация внимания, развитие креативности, творческого мышления и когнитивных навыков, зрительной и слуховой памяти, логики, наблюдательности, воображения.
Кроме того, программа обучения ментальной арифметике охватывает не только область такой точной науки, как математика, но и помогает развиваться ребенку и в других образовательных сферах. Успех, который получает ученик на занятиях, придает ему уверенность в себе и своих силах.
-
Устный счёт и интеллект.
-

Ученые выяснили, что устный счет улучшает подвижный интеллект. Подвижный интеллект, согласно теории, проявляется во всех областях жизни, но больше всего относится к научно-техническим отраслям, математике, программированию. Он включает в себя способность к обучению, индуктивному и дедуктивному мышлению, абстрактному мышлению, распознаванию связей и закономерностей. Подвижный интеллект использует рабочую память, и часто его уровень у человека вообще тесно связывают с размером рабочей памяти. Во время обучения меняется работа мозга, прокладываются новые синоптические связи. При этом электрический сигнал должен «перепрыгнуть» через щель синапса для образования новых связей между нервными клетками. Образуются новые нейронные микросети, в которые и «встраиваются» новые знания. Эту способность мозга называют нейропластичностью. Именно число микросетей в мозгу, а не его объем или масса, имеют определяющее влияние на то, что мы называем интеллект.
Таким образом, ментальная арифметика представляет собой комплекс возможностей для развития математических способностей младших школьников. Данные международных исследований подтверждают влияние данной технологии на улучшение показателей не только по математике, но и по другим дисциплинам, а также ее эффективность в повышении общих показателей интеллектуальных способностей – внимания, памяти, мышления, которые в свою очередь составляют основу для формирования математических способностей и гармоничного развития личности.
-
Рождение навыка
Одной из главных задач изучения ментальной арифметики является развитие и формирование у младших школьников устойчивых и осознанных вычислительных навыков. В настоящее время можно сделать вывод о том, что формирование навыков вычислений зависит от понимания выполняемых учеником действий, умения правильно и быстро вычислять.
Навыки вычисления необходимы не только для учения, а и в повседневной жизни каждого человека. У детей развитие этих навыков должно быть осознано и стойко. Для успешного формирования у учеников вычислительных навыков в учебном процессе создан ряд определенных условий. Так как процесс усвоения вычислительных навыков достаточно непростой, изначально учащиеся осваивают определенные приемы, а далее в результате постоянных повторений уже своевременно быстро выполняют вычисления. Вычисления составляют определенное число последовательных действий и операций, которое в свою очередь составляет определение теоретической основы вычислительных приемов.
Вычислительный навык – это высокая степень овладения вычислительными приёмами. Приобрести вычислительные навыки - значит для каждого случая знать, какие операции и в каком порядке следует выполнять, чтобы найти результат арифметического действия и выполнять эти операции достаточно быстро. Полноценный вычислительный навык характеризуется правильностью, осознанностью, рациональностью, обобщенностью, автоматизмом, прочностью.
Правильность - ученик правильно находит результат арифметического действия, то есть правильно выбирает и выполняет операции, составляющие приём.
Осознанность – ученик осознает, на основе каких знаний выбраны операции и установлен порядок их выполнения, в любой момент может объяснить, как он решал и почему так можно решать. Рациональность – ученик выбирает для данного случая более рациональный приём, то есть выбирает те из возможных операций, выполнения которых легче других и быстрее приводит к результату.
Обобщенность – ученик может применить приём вычисления к большому числу случаев, то есть способен перенести приём вычисления на новые случаи.
Автоматизм – ученик выполняет и выделяет операции быстро и в свернутом виде, но всегда может вернуться к объяснению выбора системы операций. Высокая степень автоматизации должна быть достигнута по отношению к табличным случаям сложения и вычитания, умножения и деления.
Прочность – ученик сохраняет сформированные вычислительные навыки на длительное время.
Формирование у школьников вычислительных навыков остается одной из главных задач начального обучения математике, поскольку вычислительные навыки необходимы как в практической жизни человека, так и в учении. Эти навыки должны формироваться осознанно и прочно, так как на их базе строится весь начальный курс обучения математике.
Вычислительный навык — это высокая степень овладения вычислительными приёмами. Приобрести вычислительные навыки – значит, для каждого случая знать, какие операции и в каком порядке следует выполнять, чтобы найти результат арифметического действия и выполнять эти операции достаточно быстро.
| уровни
критерии | высокий | средний | низкий |
| правильность | ученик правильно находит результат арифметического действия над данными числами
| ребенок иногда допускает ошибки в промежуточных операциях | ученик часто неверно находит арифметические действия |
| осознанность | ученик осознает на основе, каких знаний выбраны операции, может объяснить решение примера | ученик осознает на основе, каких знаний выбраны операции, но не может объяснить, почему решал так, а не иначе | ребенок не осознает порядок выполнения операций |
| рациональность | ученик выбирает для каждого случая более рациональный прием, может из нескольких приемов выбрать более рациональный | ученик выбирает для каждого случая более рациональный прием, но не в стандартных условиях знания применить не может | ребенок не может выбрать операции, выполнения которых быстрее приводит к результату арифметического действия |
| автоматизм | ученик выделяет и выполняет операции быстро в свернутом виде
| ученик не всегда выполняет операции быстро в свернутом виде | ученик медленно выполняет систему операций, объясняя каждый шаг |
| обобщенность | ученик может применить прием вычисления к большему числу случаев, то есть он способен перенести прием вычисления на новые случаи | ученик может применить прием вычисления к большему числу случаев только в стандартных условиях | ученик не может применить прием вычисления к большему числу случаев |
| прочность | ученик сохраняет сформированные вычислительные навыки на длительное время | ученик сохраняет сформированные вычислительные навыки на короткий срок | ребенок не сохраняет сформированные вычислительные навыки |
Этапы работы над вычислительным приемом.
1. Подготовка к принятию нового приема.
На этом этапе создается готовность к усвоению вычислительного приема, а именно: учащиеся должны усвоить те теоретические положения, на которых основывается вычислительный прием, а также овладеть каждой операцией, составляющей прием.
2. Ознакомление с вычислительным приемом.
На этом этапе ученики усваивают суть приема, какие операции надо выполнять, в каком порядке и почему именно так можно найти результат арифметического действия. Выполнение каждой операции важно сопровождать пояснениями вслух. Сначала эти пояснения выполняются под руководством педагога , а затем учащиеся выполняют их самостоятельно.
3. Закрепление знания приема и выработка вычислительного навыка.
На этом этапе учащиеся должны твердо усвоить систему операций, составляющих прием, и предельно быстро выполнять эти операции, т. е. овладеть вычислительным навыком.
В процессе работы здесь важно предусмотреть ряд стадий в становлении у учащихся вычислительных навыков:
а) на первой из них закрепляется знание приема;
б) на второй – происходит частичное свертывание выполнения операций;
в) на третьей - происходит полное свертывание выполнения операций.
Овладение учащимися вычислительными навыками достигается в результате многократного числа тренировочных упражнений. Важно, чтобы они были разнообразными как по числовым данным, так и по форме, чтобы при этом предусматривались аналогии в приемах и в соответствии с ними предлагались упражнения на сравнение приемов, сходных в том или ином отношении.
Таким образом, вычислительные навыки успешно формируются у учащихся при создании в учебном процессе определённых условий: сначала ученики должны усвоить тот или иной вычислительный прием, а затем в результате тренировки научиться достаточно быстро выполнять вычисления, а в отношении табличных случаев — запомнить результаты наизусть.
-
От сложения и вычитания к умножению и делению.
Действия, которые мы производим с числами: сложение, вычитание, умножение, деление. Действия с однозначными числами легкие, трудности возникают при счете многозначных чисел.
При переходе к Умножению в начале обучают младших школьников составлению и усвоению таблиц умножения и деления. В процессе изучения смысла умножения ученики осваивают табличные случаи умножения. На этом этапе учащимся предлагают интересные задания и упражнения, которые способствуют рефлекторному усвоению материала и таблицы умножения
-
Основные постулаты при изучении темы умножение и деление:
-
Умножение – это многократное сложение одинаковых множителей
-
Компоненты умножения и переместительный закон умножения.
1.6.
Правила умножения, помогающие понять суть умножения, уметь вычислить табличные и вне табличные примеры и запомнить результат умножения.
-
При умножении числа на 1 получается само число.
-
При умножение числа на 2, нужно сложить число с самим собой
-
При умножении числа на 3, число складывается с собой 2 раза.
-
При умножении числа на 4, нужно сложить число само с собой, и к результату прибавить столько же.
-
При умножении числа на 5, просто умножить число на 10, а потом поделить пополам.
-
При умножении числа на 6, проще умножить на 3, а потом прибавить столько же.
-
При умножении числа на 7, нужно умножить его на 10, а затем вычесть 3 раза. Или умножить на 6, как в пункте 6, а потом прибавить ещё раз это число.
-
При умножении на 8, нужно число умножить на 4, а потом прибавить столько же, или умножить на 10 и вычесть 2 раза само число.
-
При умножении на 9, можно число умножить на 3, потом результат ещё раз умножить на три, но проще умножить на 10 и вычесть число.
-
При умножении на 10 – дописываем нолик справа
-
Необходимые навыки для изучения темы Умножение в Ментальной арифметике:
-
Развитые навыки счета трехзначных чисел темы Анзан на абакусе
-
Сформированный навык ментального счёта темы Анзан до трехзначных чисел.
-
Понимание сути умножения и четкие знания результатов умножения однозначных чисел.
-
Понимание терминологии ментальной арифметики и математических операций. (верхние косточки, планка, левый крайний ряд, множитель, произведение, сумма и т.д.)
2.1. Алгоритм выполнения действия умножения на абакусе рассмотрим на примерах
Пример №1 15*7
Итак: 15-первый множитель, 7-второй множитель. В результате вычислений получим произведение.
В 1 множителе одна цифра, в втором множителе 2 цифры, всего в 2 множителях 3 цифры, это означает, что в произведении будет не более 3 цифр. Начинаем вычисления. Первый множитель отметим на крайних спицах слева, а второй множитель на крайних спицах справа. В последствии можно не откладывать числа, а сразу вычислять ответ.
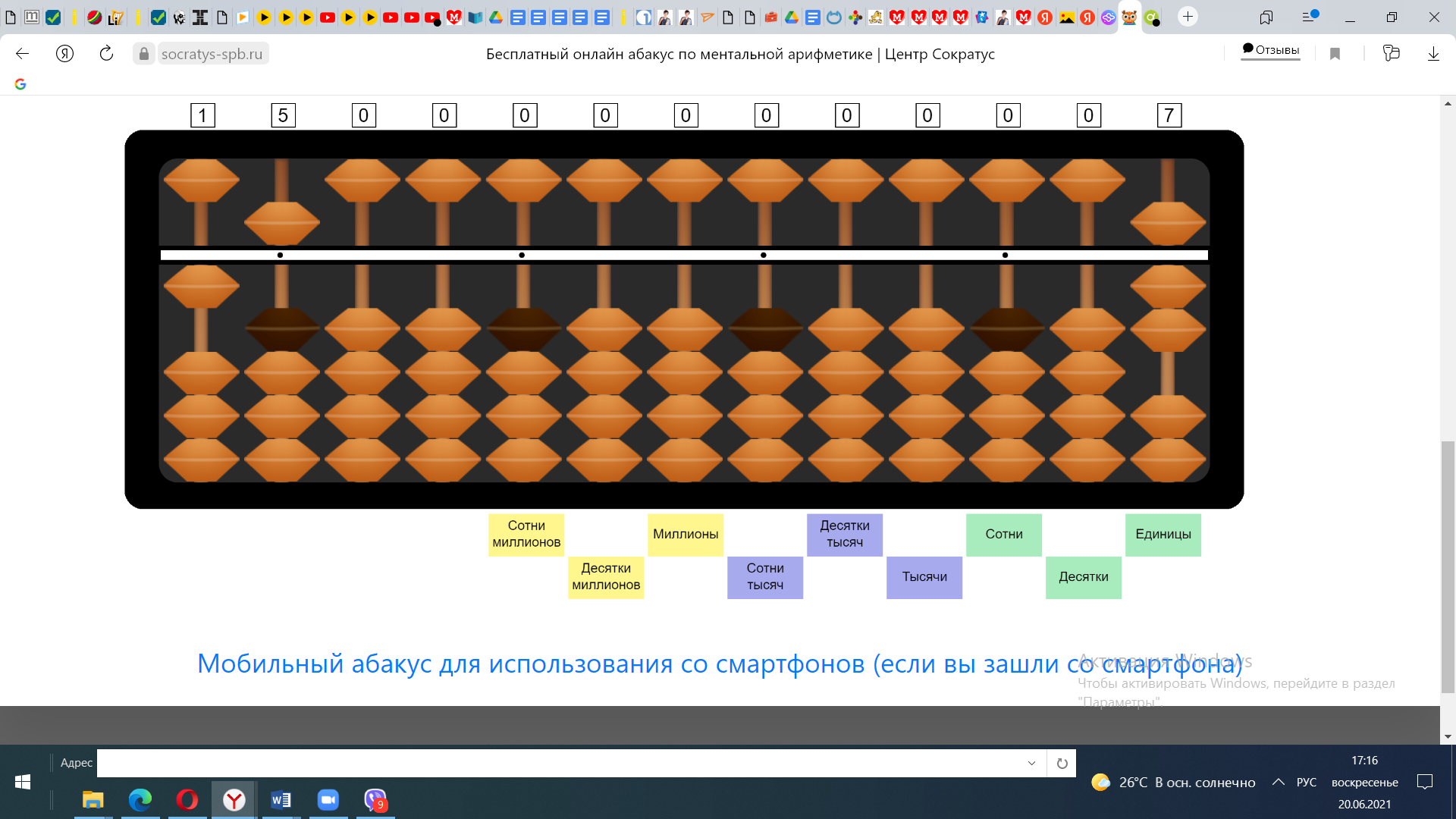
1) Десятки первого множителя умножаем на единицы второго множителя (потому что второй множитель состоит только из единиц) 10 умножим на 7 = 70.
ВАЖНО! Ответ в умножении будет откладывать НЕ на крайних спицах справа как при сложении и вычитании, а слева от 6 спицы (вторая точка справа).
Откладываем 70.

2) Единицы первого множителя умножаем на единицы второго множителя. 3*7=35
3) Прибавляем 35 к 70. Получаем ответ 105.
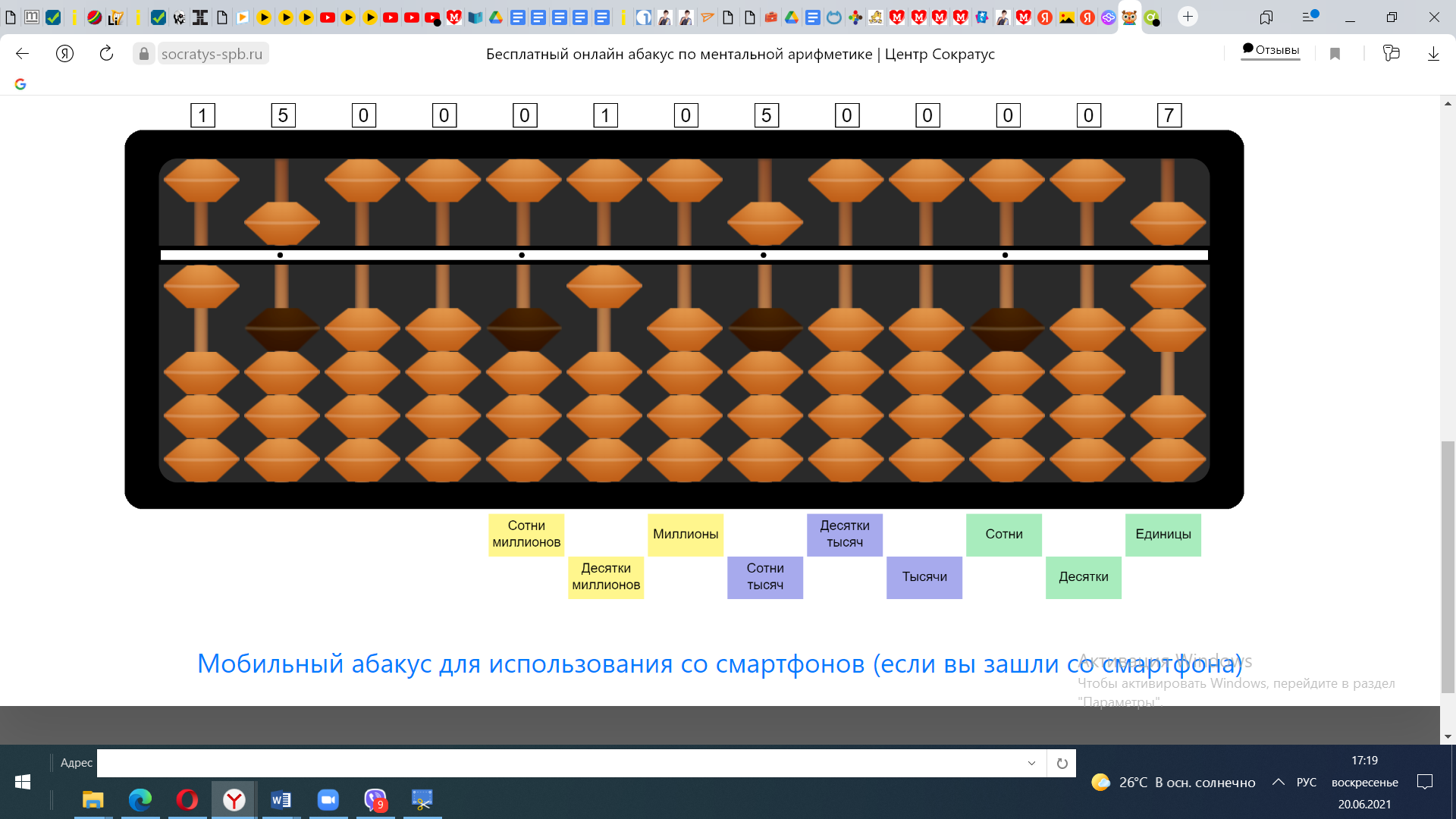
Пример №2 93*8
Число 93 отложим на 2 спицах слева, число 8 отложим справа
1) 90*8=720 Откладываем 720 на абакусе.
2) 3*8=24 Прибавляем к 720 - 24. Получаем ответ 744

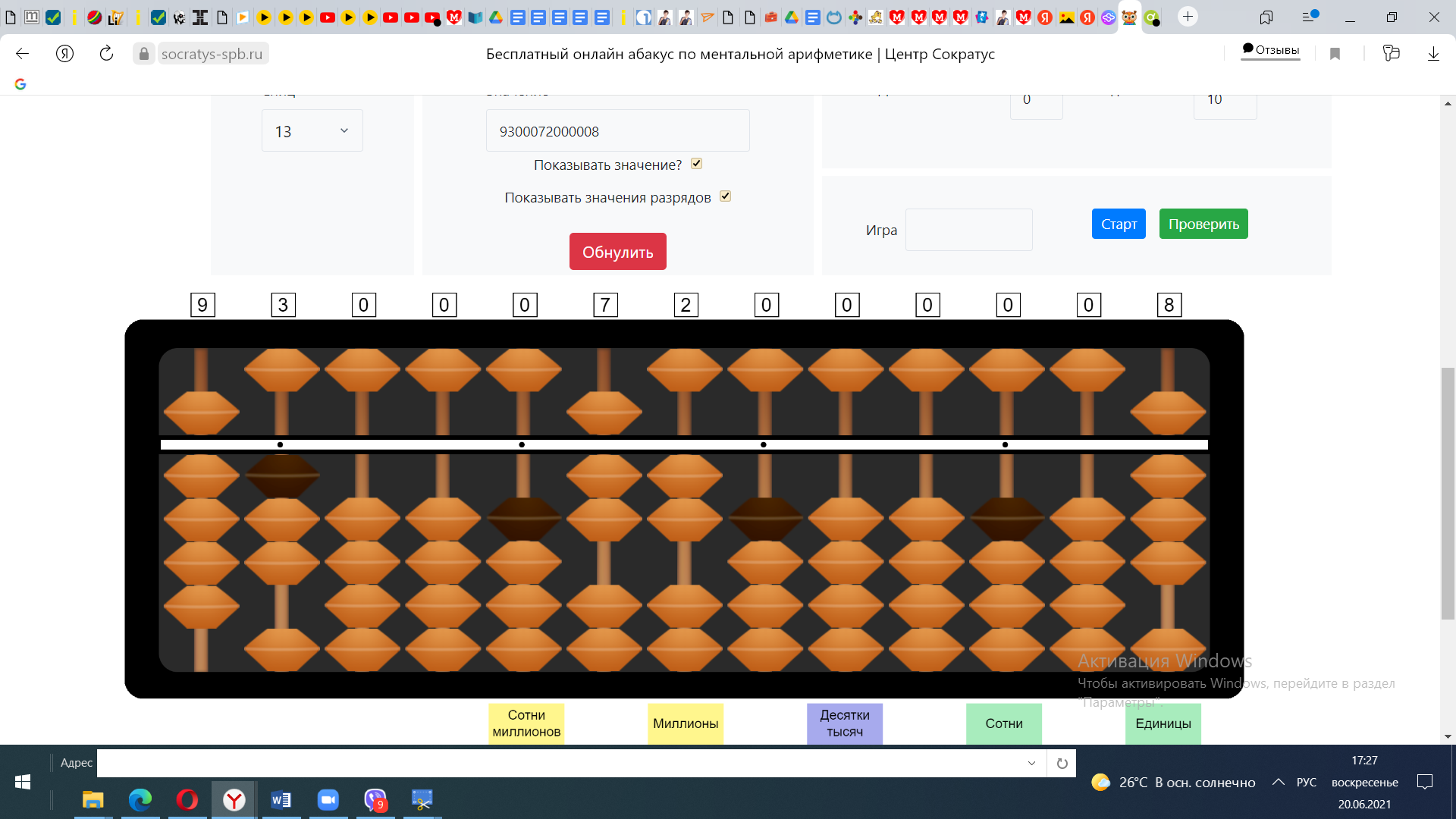
Пример №3 156*4
1) 100*4=400 Откладываем 400 на абакусе.
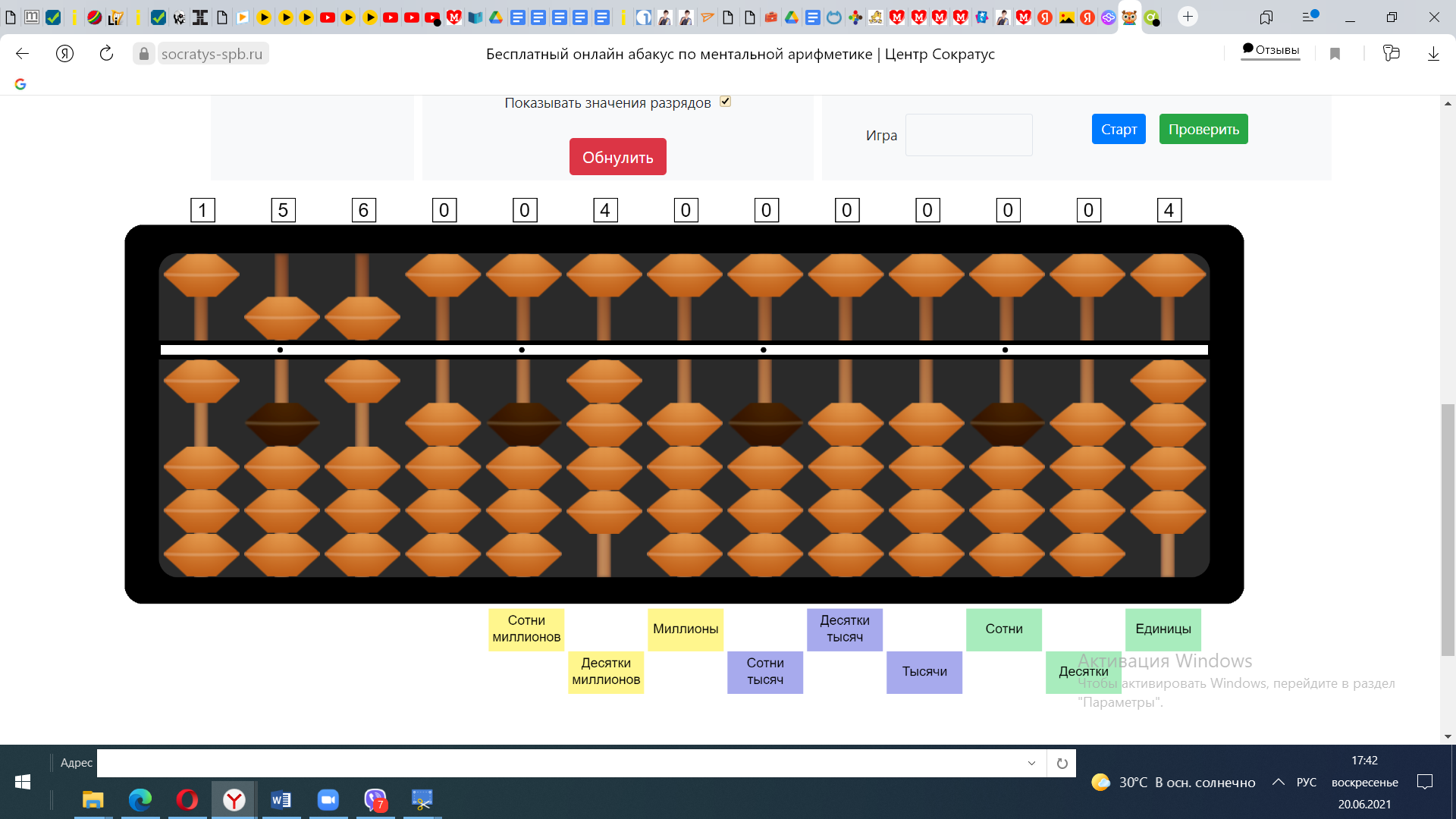
2) 50*4=200 Прибавляем 200 к 400
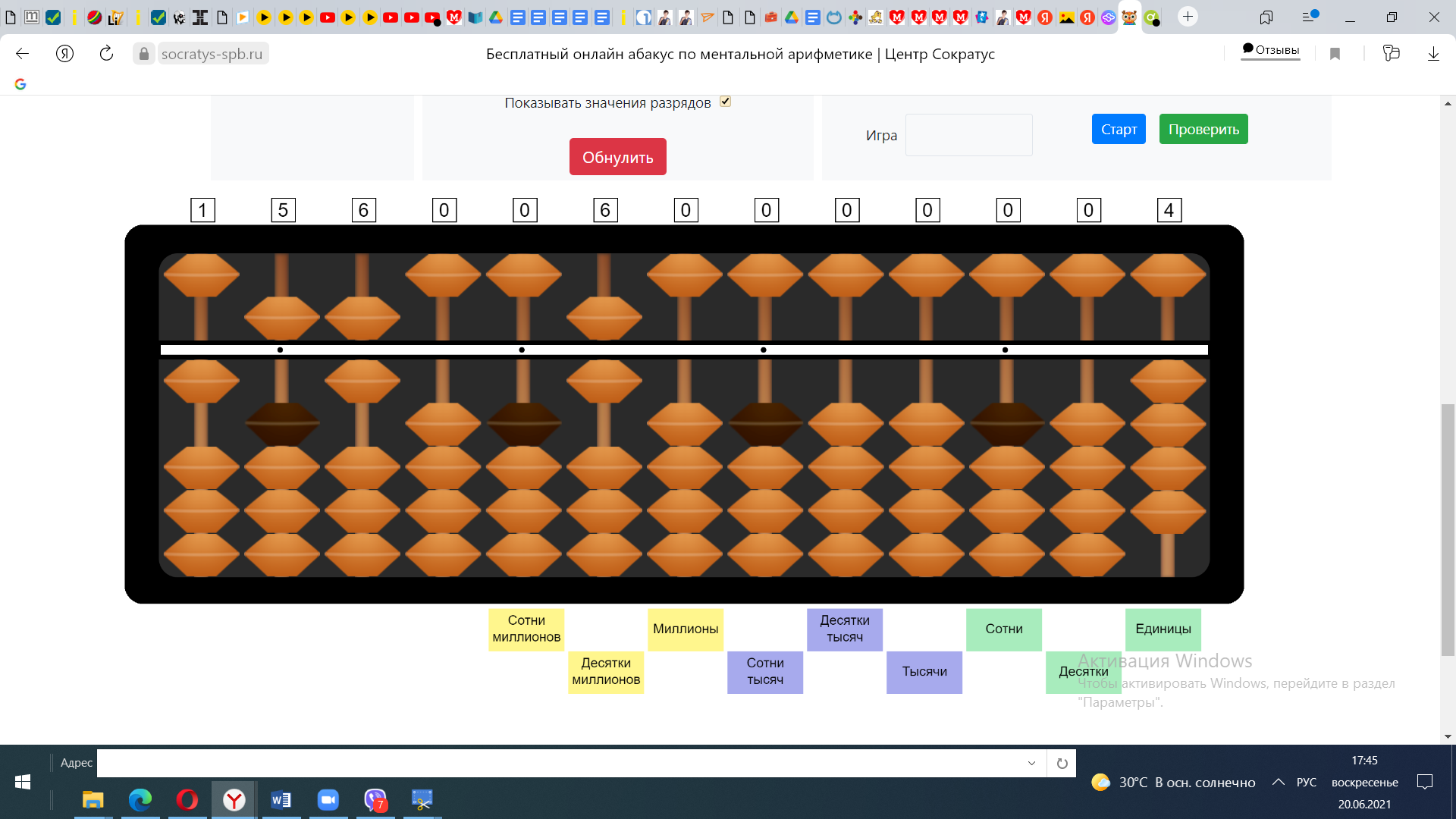
3) 6*4= 24 Прибавляем 24. Получаем ответ 624

Пример №4 Умножение на двузначное число
12*15
Расположим множители так же как и при умножении на однозначное число
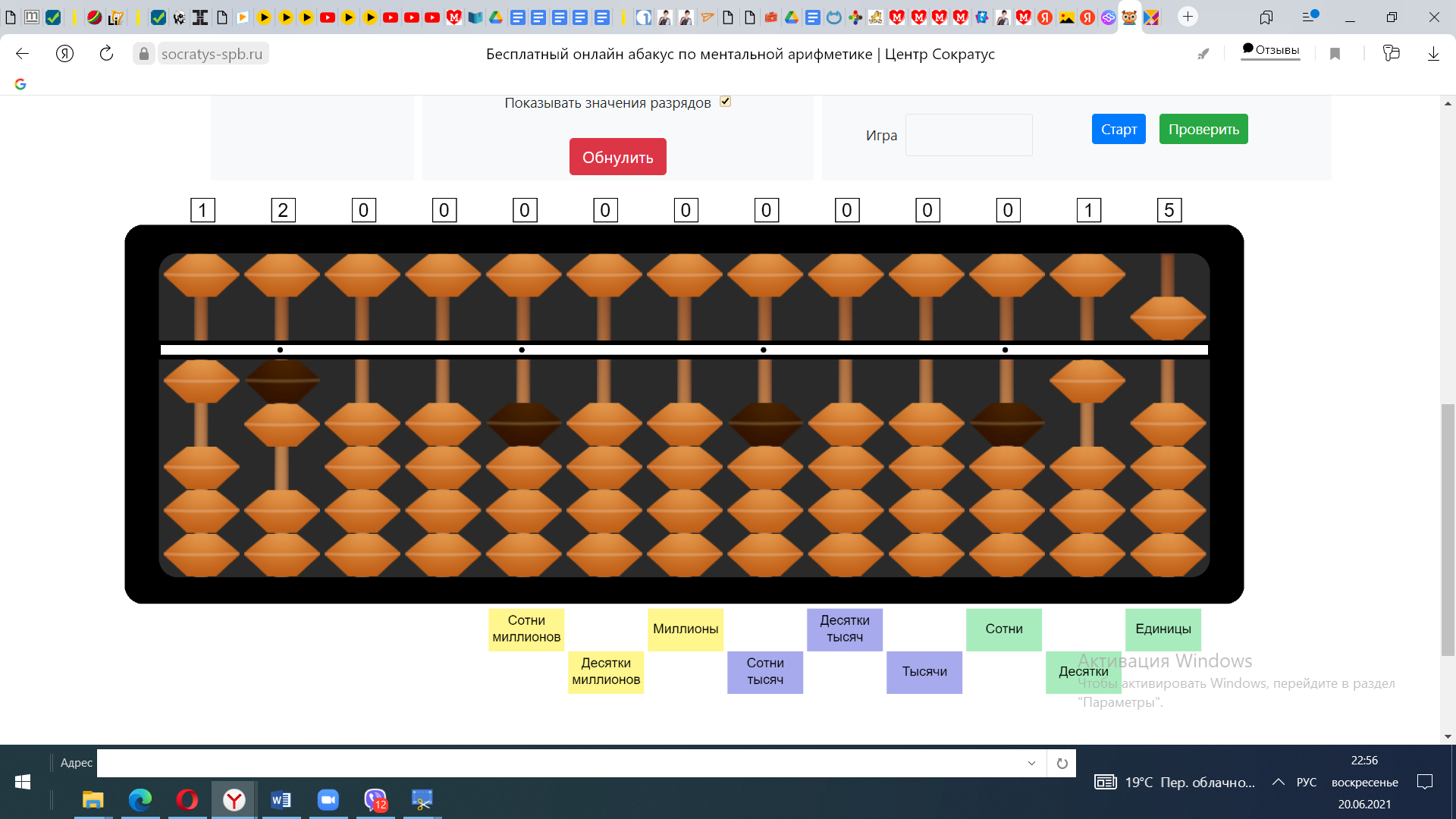
1) Десятки первого множителя умножим на десятки второго множителя 10*10=100. Отложим число 100 на абакусе.
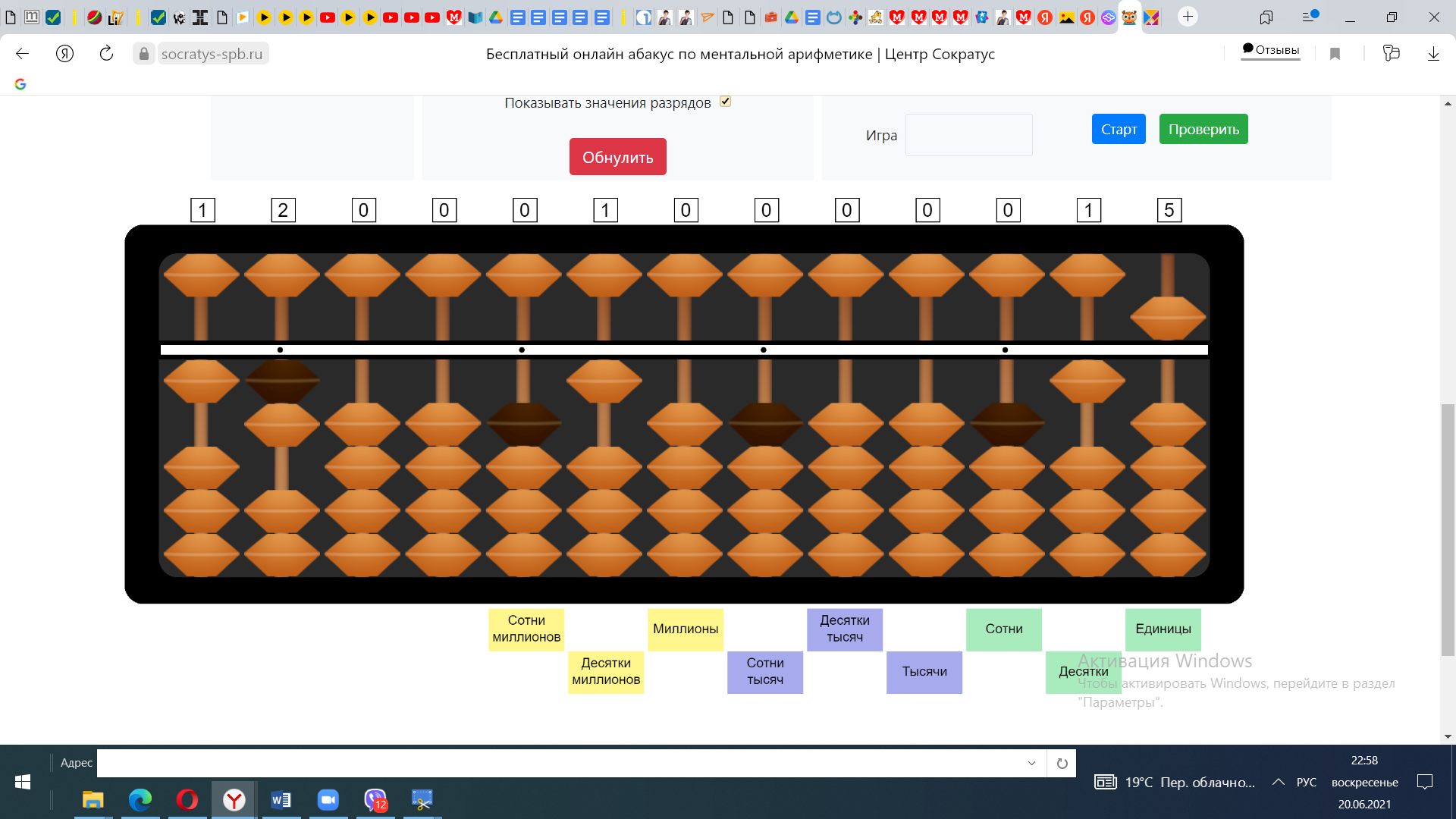
2) Единицы первого множителя умножим на десятки второго множителя. 2*10=20. Прибавим 20 к 100
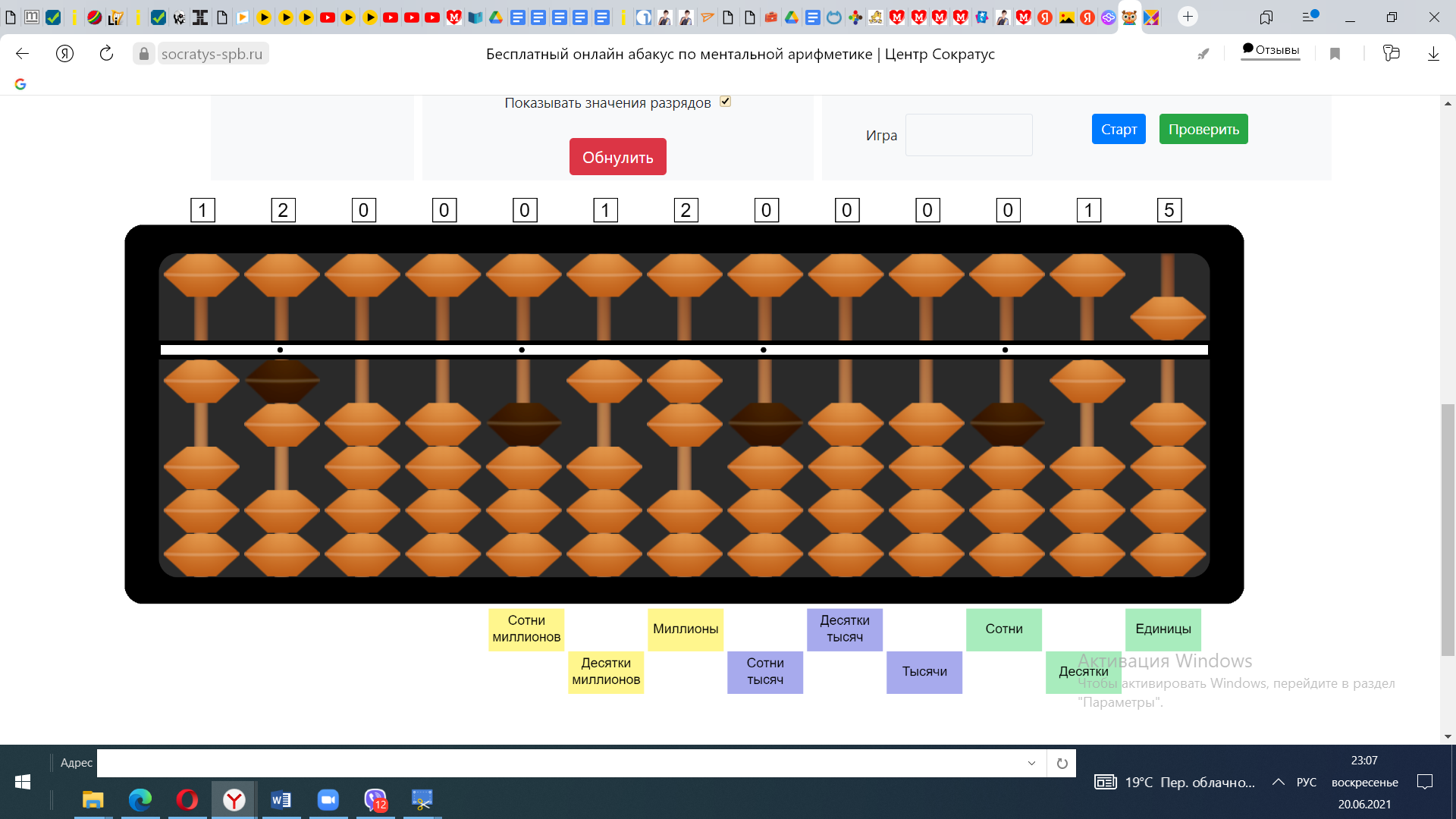
3) Десятки первого множителя умножим на единицы второго множителя. 10*5=50. Прибавляем 50 к числу 120.
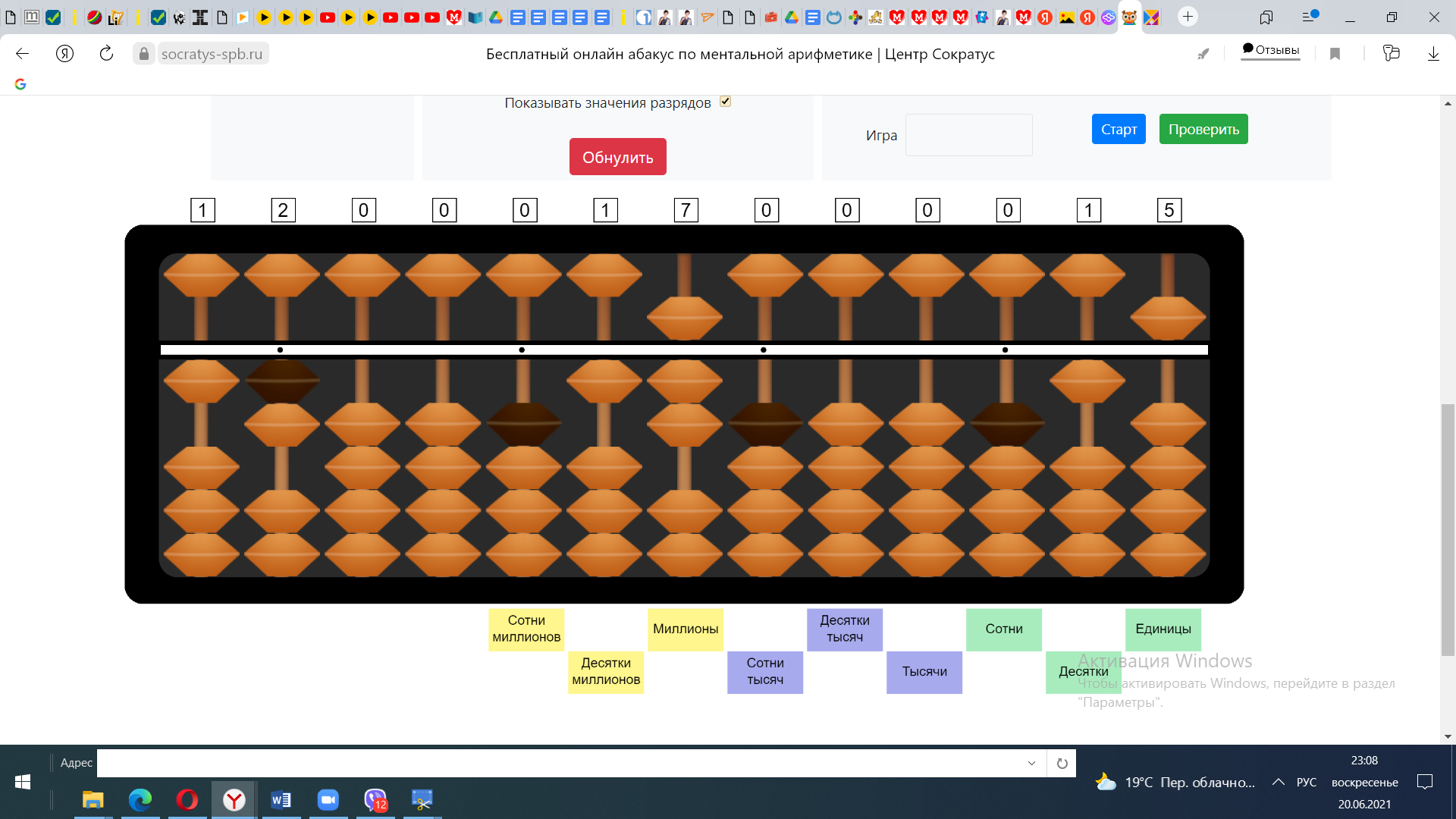
4) Единицы первого множителя умножаем на единицы второго множителя 2*5=10. Прибавляем 10 к 170 и получаем ответ 180
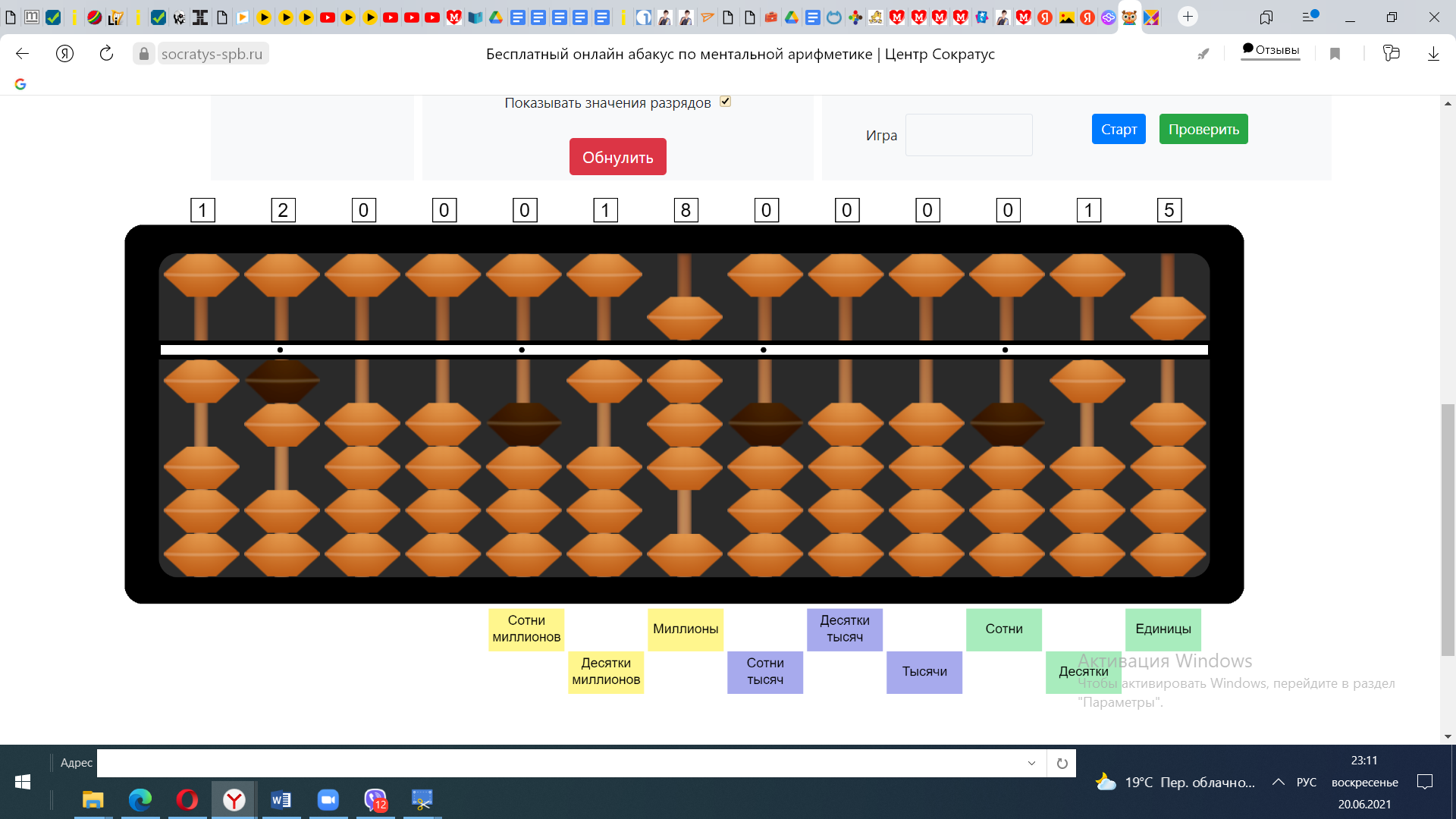
Пример №5 45*38
1) 40*30=1200
2)40*8=320 1200+320=1520
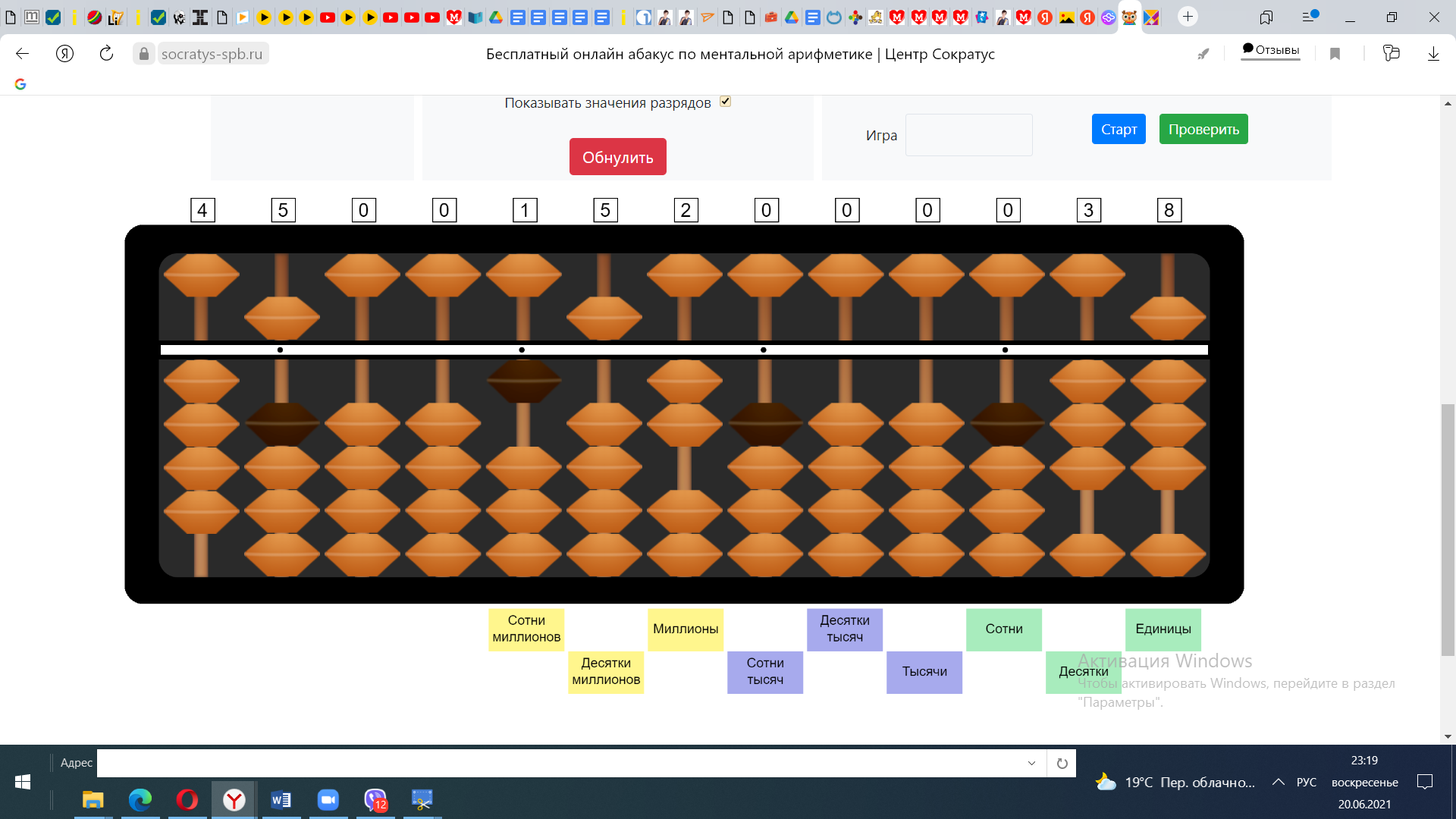
3) 5*30=150 1520+150=1670
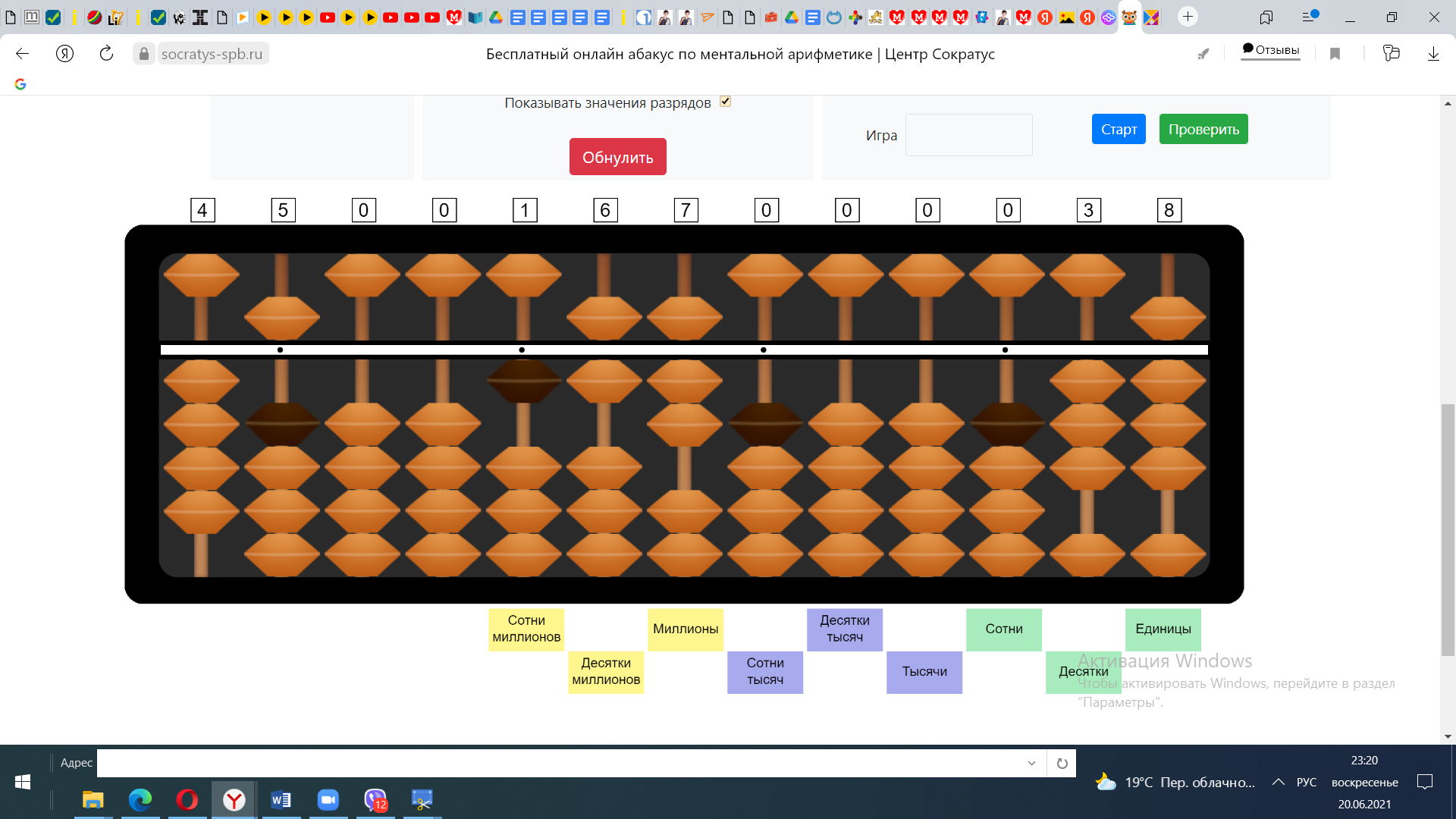
4) 5*8=40 1670+40=1710
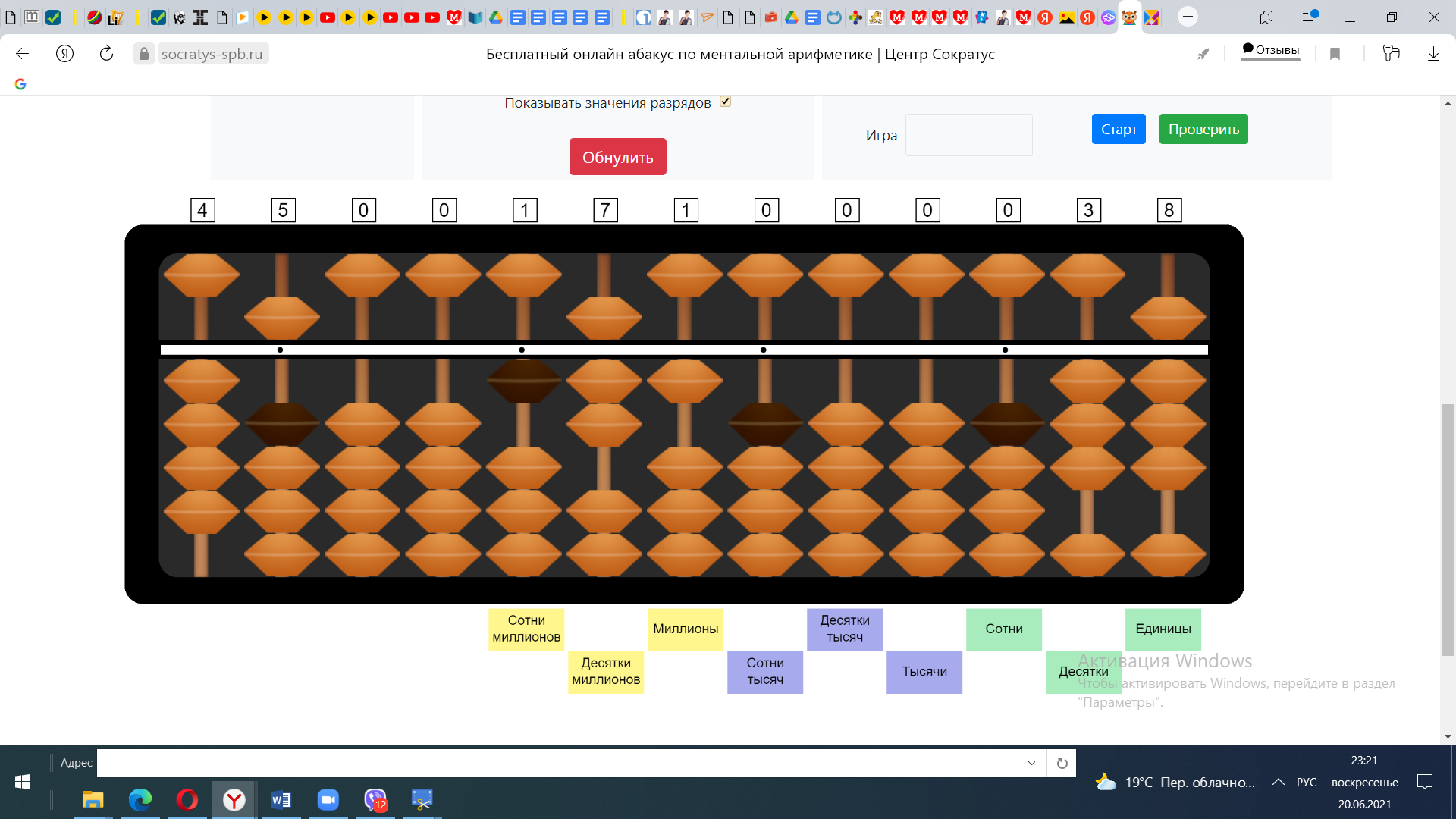
Ответ: 1710
Пример №6 Умножение трехзначного числа на двузначное 627*52
1) 600*50=30000
2) 600*2=1200 30000+1200=31200
3) 20*50=1000 31200+1000=32200
4)20*2=40 32200+40=32240
5)7*50=350 32240+350=32590
6)7*2=14 325900+14=32604
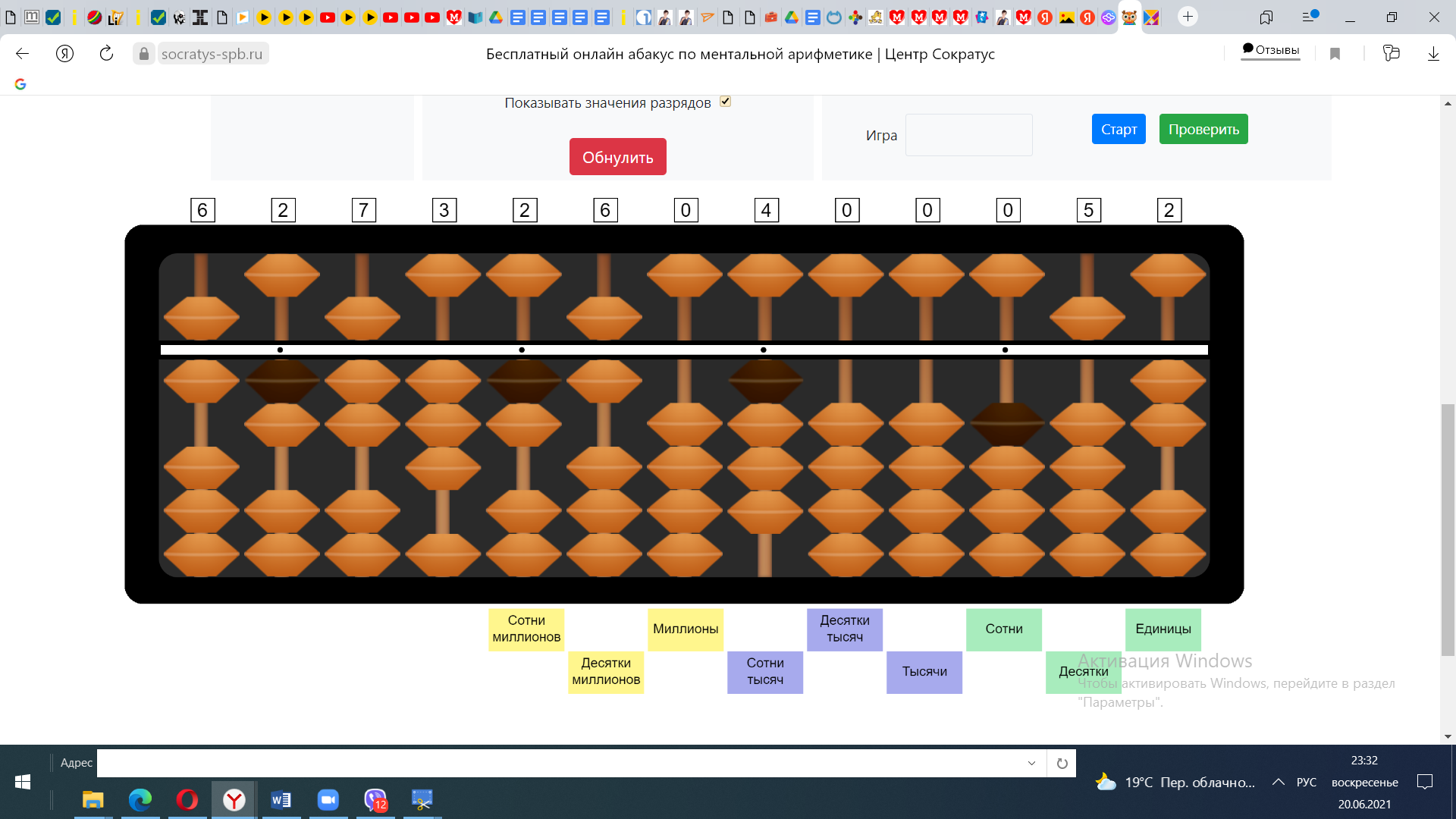
Деление
Деление – это действие обратное умножению. Само слово знакомо детям с детства, ведь с раннего возраста малыш что-то делит, распределяет.
Распределение - это суть операции деления. Так, если поровну распределить четыре яблока между двумя людьми, у каждого из них будет по два яблока.
Деление позволяет найти, сколько раз одно число содержится в другом.
Процесс деления можно показать ребенку и так:
-
если 10 конфет раздать 2 людям, то каждый получит по 5 конфет;
-
если 10 конфет, разложенные в кучки по 2 конфеты, дадут 5 кучек.
Признаки делимости
Рассмотрим очень полезную таблица, ведь по ней мы всегда сможете узнать, делится ли любое большое число на 1,2,3…10.
Деление в ментальной арифметике
В делении больше динамики, чем в умножении. Делимое и делитель нужно расположить на крайних левых спицах и отделить свободной спицей между ними. Ответ будем записывать справа от 6 спицы (спица, помечена второй точкой справа). Рассмотрим алгоритм деления на примерах.
Деление на однозначное число
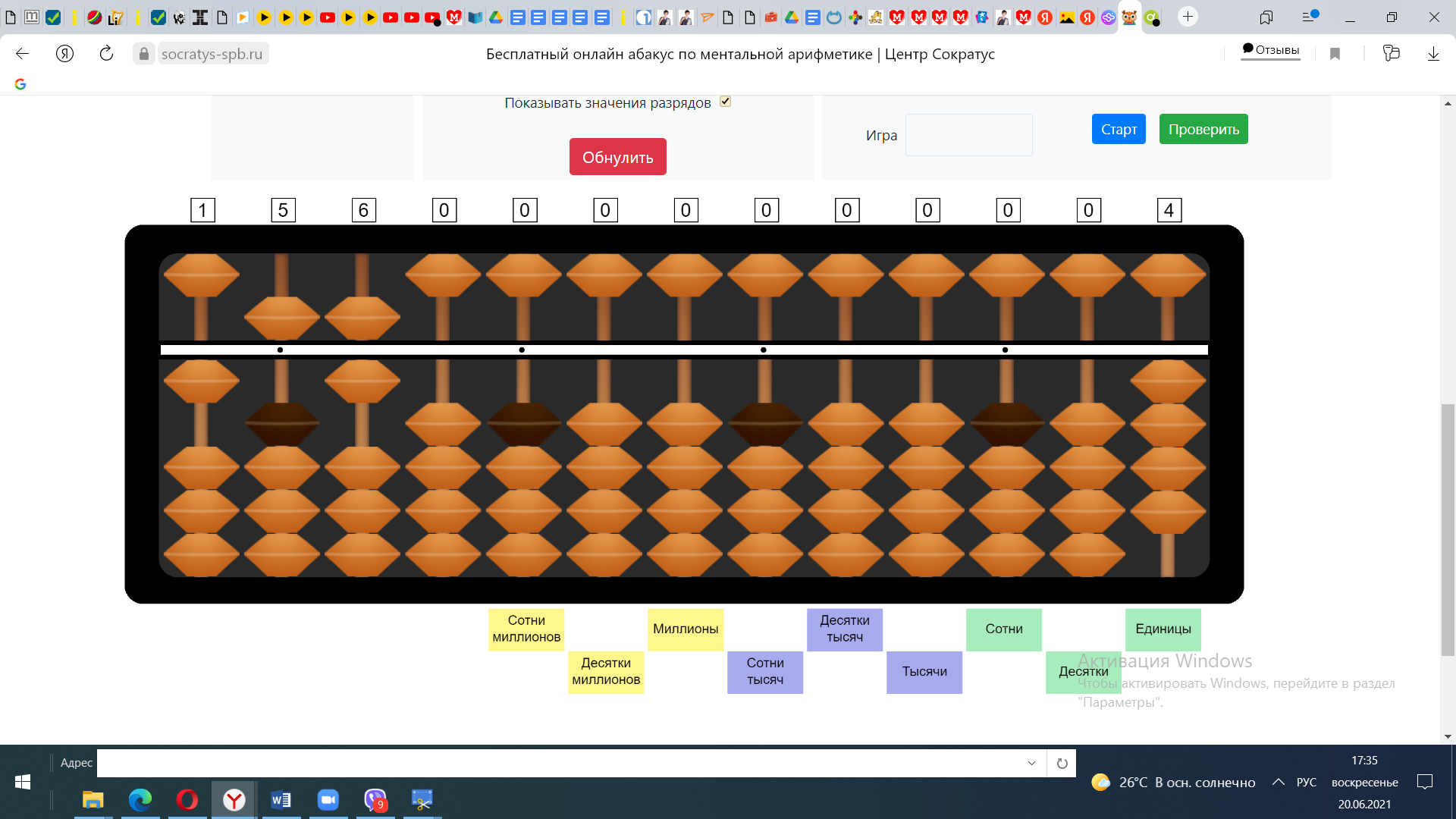
Пример №1 36:2 Откладываем Делитель на крайней левой спице, оставляем следующую спицу пустой и после неё откладываем делимое.
1) Определим сколько цифр будет в частном. В примере 36:2 в частном будет 2 цифры. Определим визуально 2 спицы на которых будет набран ответ.
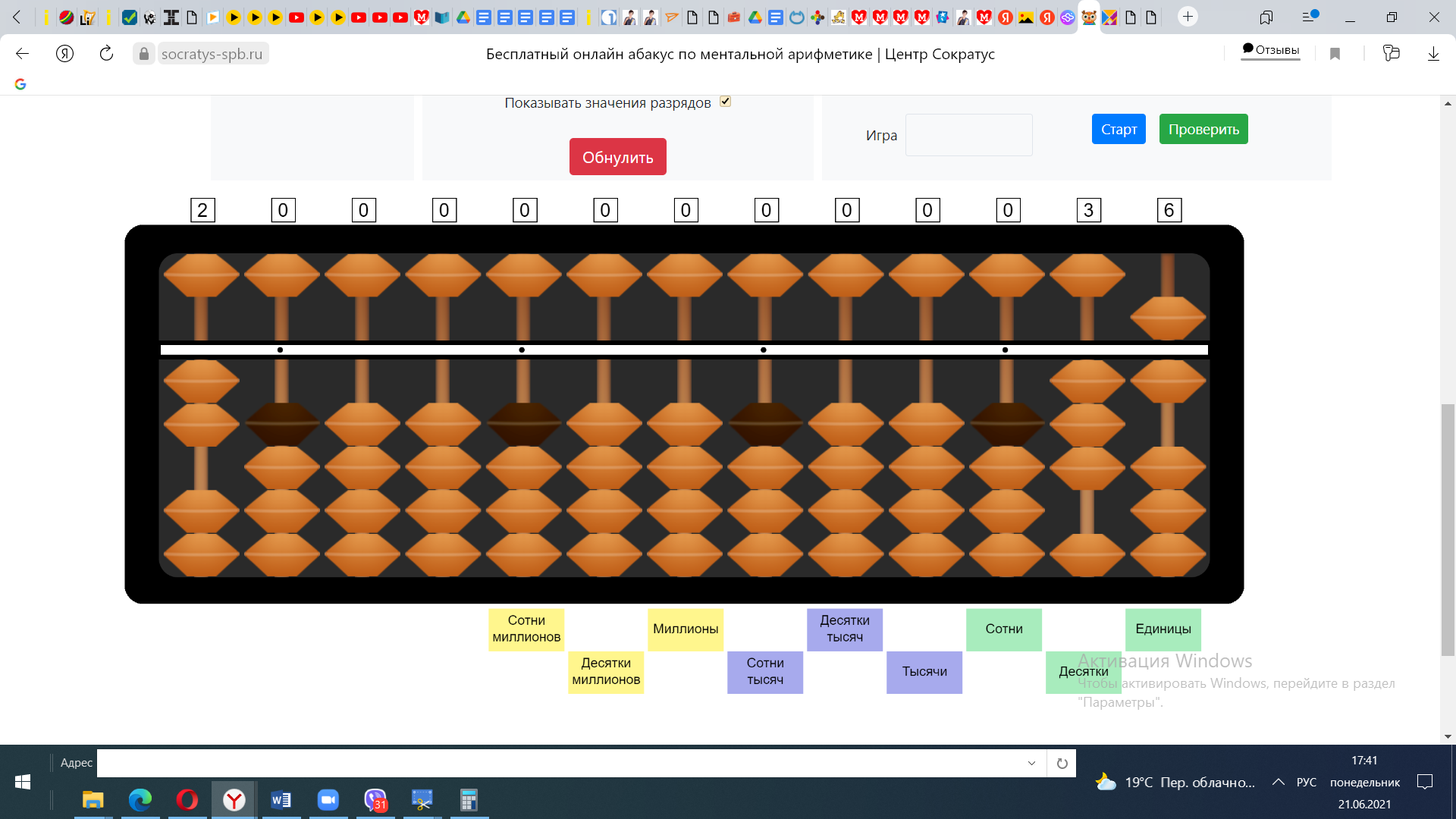
2) число старшего разряда делимого поделим на число старшего разряда делителя. В нашем примере № нужно поделить на 2. Зададим вопрос: сколько раз в числе 3 убирается число 2. Конечно 1 раз. Набираем число 1 на нужной спице.
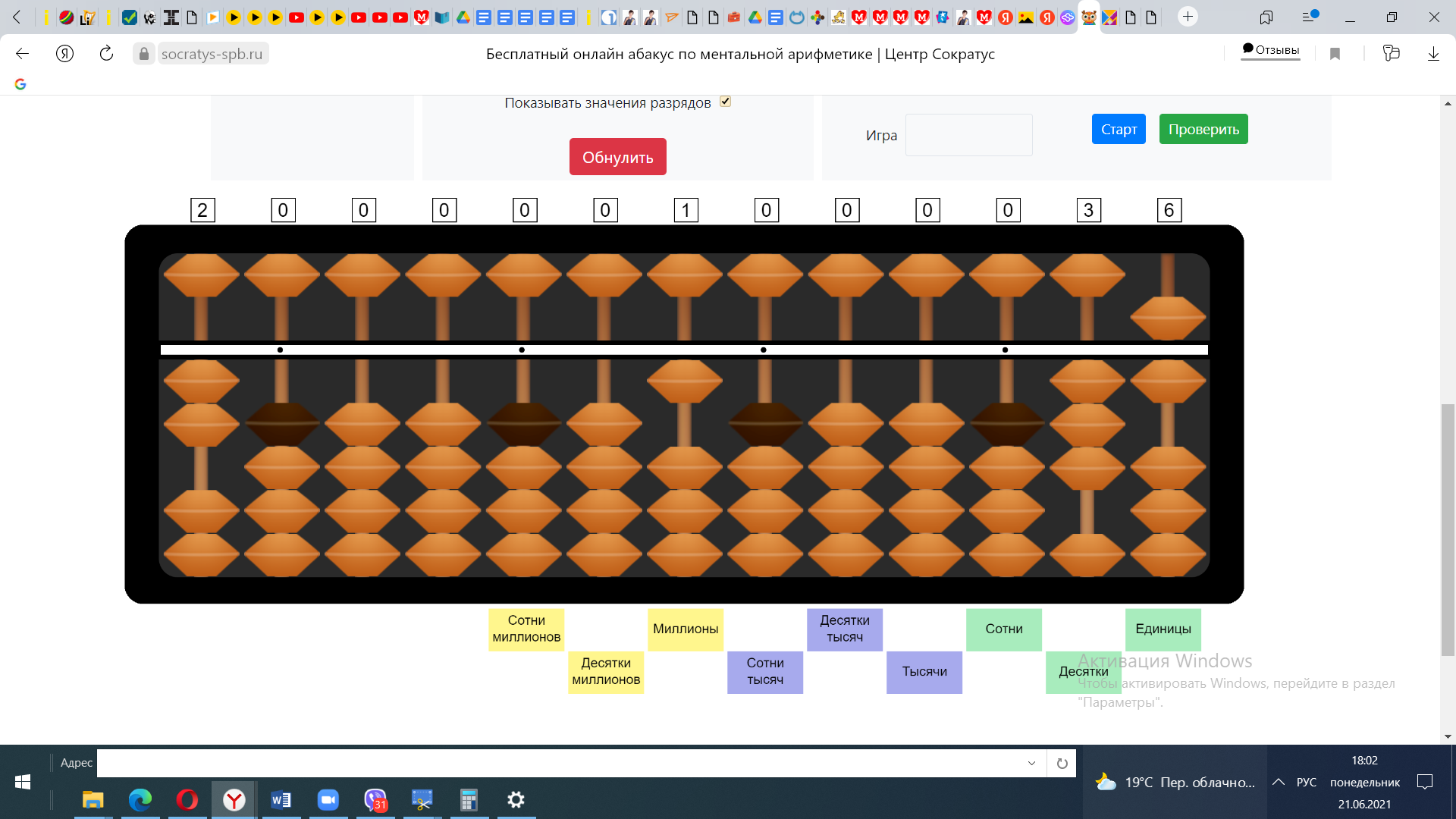
3) Умножим 2 на 1, получим два. Отнимем от 3 полученное число 2, получим 1 – это остаток. Смотрим какое число получилось – 16. 16:2=8. Откладываем число 8 на спице справа от числа 1. Получаем ответ 18.
Пример №2 72:4
Откладываем делимое и делитель. Определяем количество цифр в частном (2 цифры), визуально выделяем спицы, на которых будет ответ.
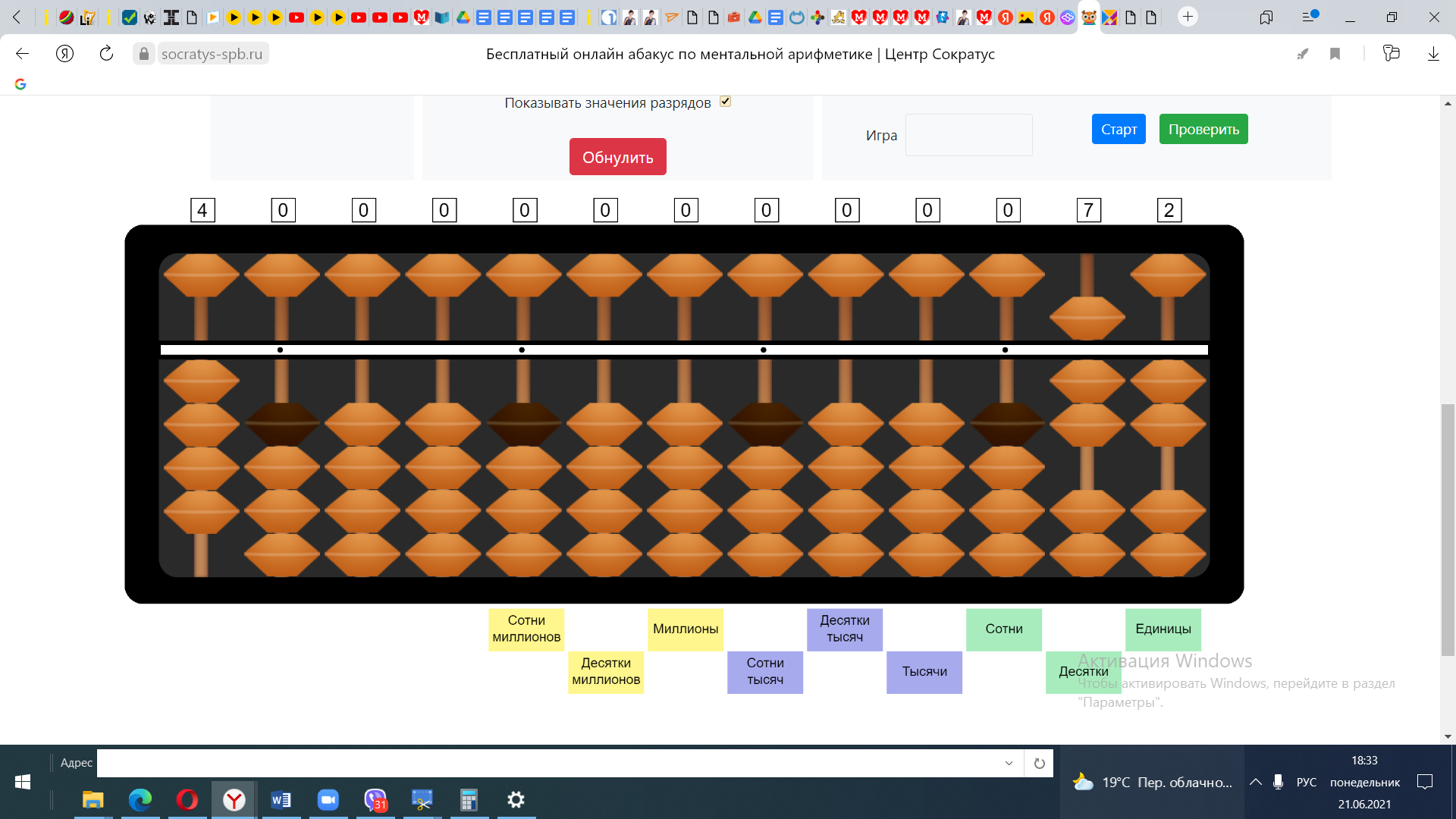
1) 7:4 В числе 7 убирается одна 4, откладываем число 1 на нужной спице.

2) 1*4=4 Из 7 вычитаем 4, получаем остаток 3.
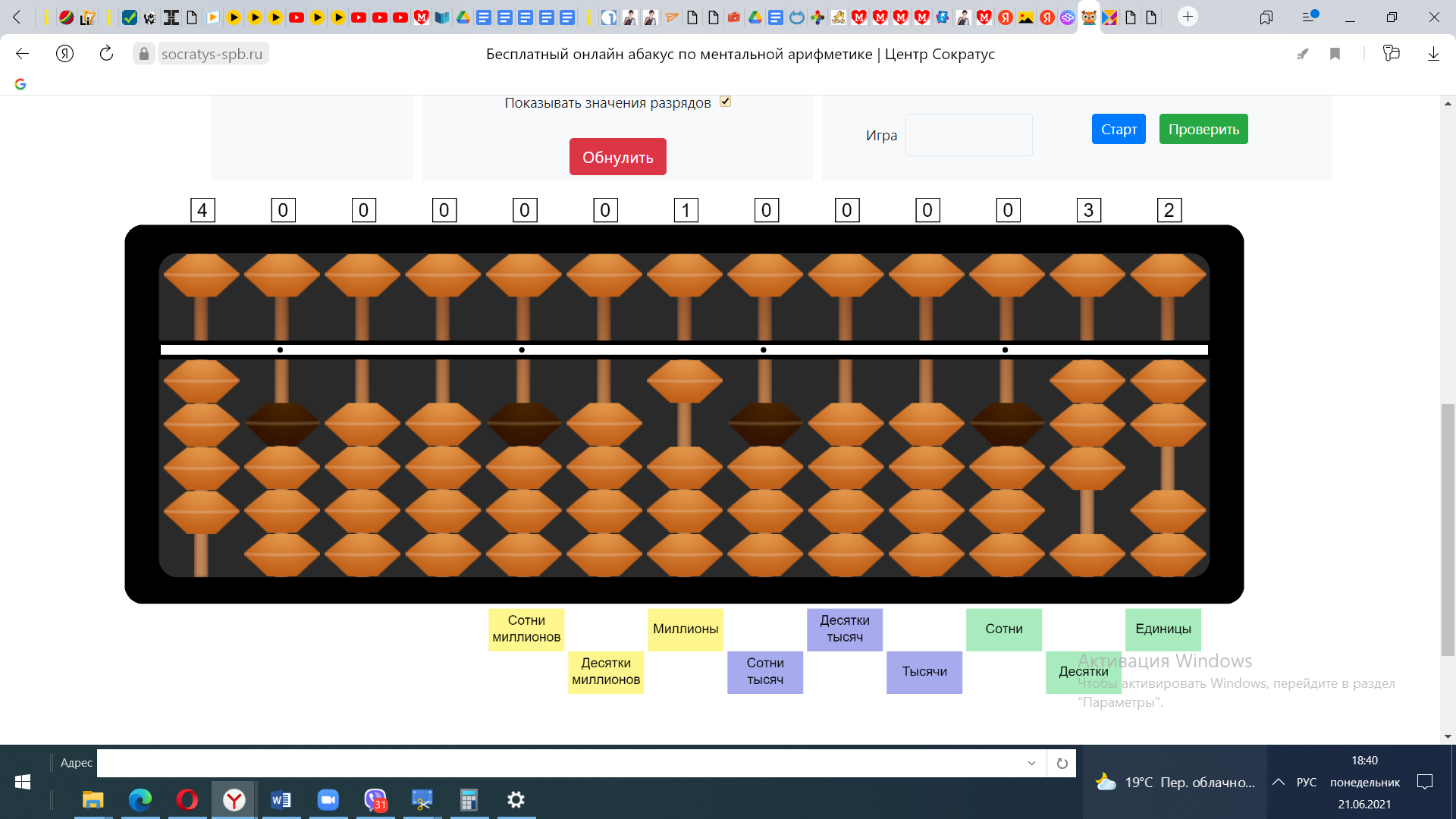
3) Продолжим деление. У нас осталось число 32. 32:4=8. Откладываем 8 на спице справа от числа 1. Получаем ответ=18
Пример№3 190:5
Отложим делимое и делитель, определим из скольких цифр будет состоять частное (из 2), наметим визуально спицы на которых будем откладывать ответ.
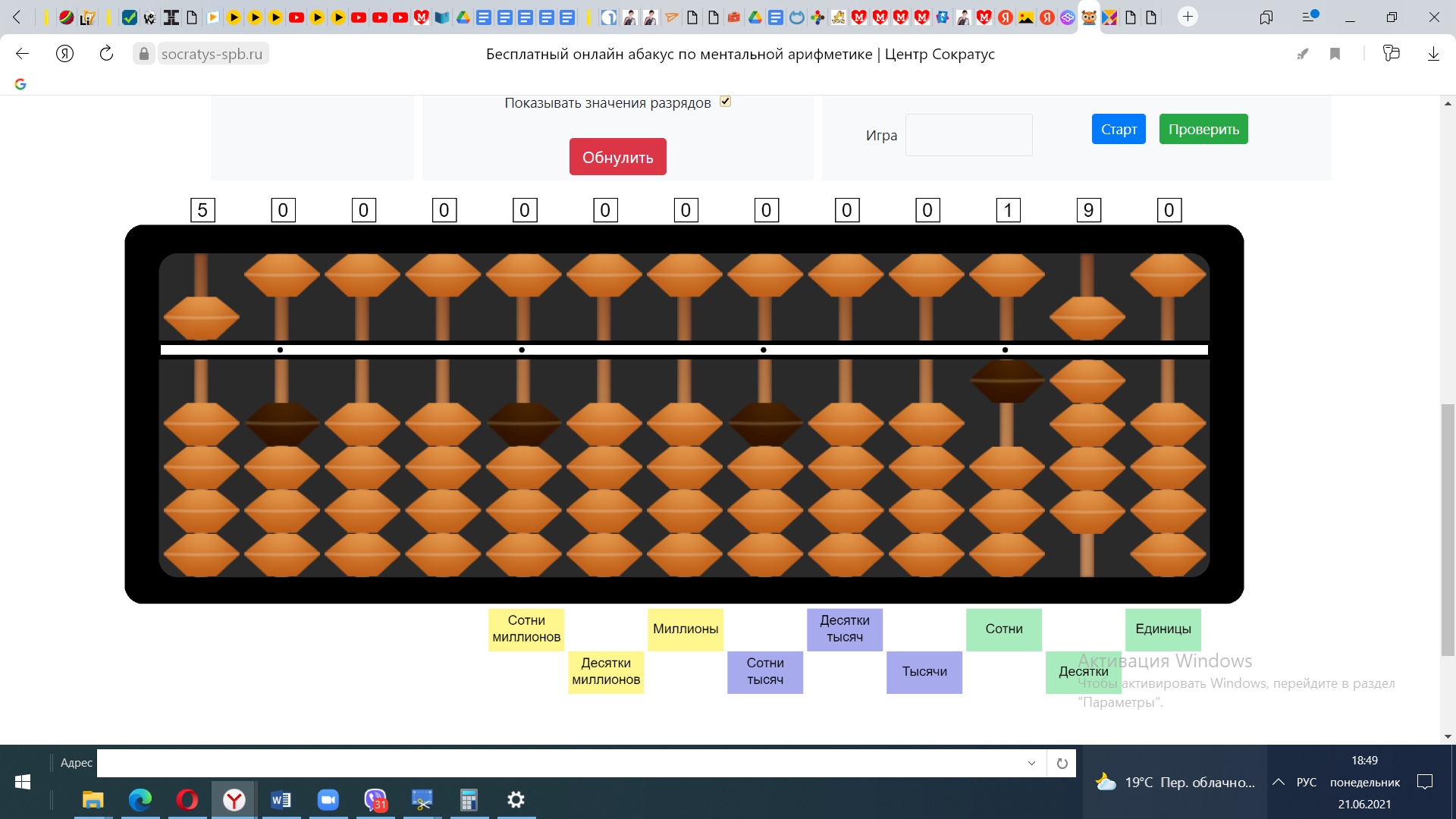
1) В числе 1 число 5 не убирается ни сколько раз, по этому берём число 19. В числе 19 число 5 убирается 3 раза. Откладываем число 3 в разряде десятки.
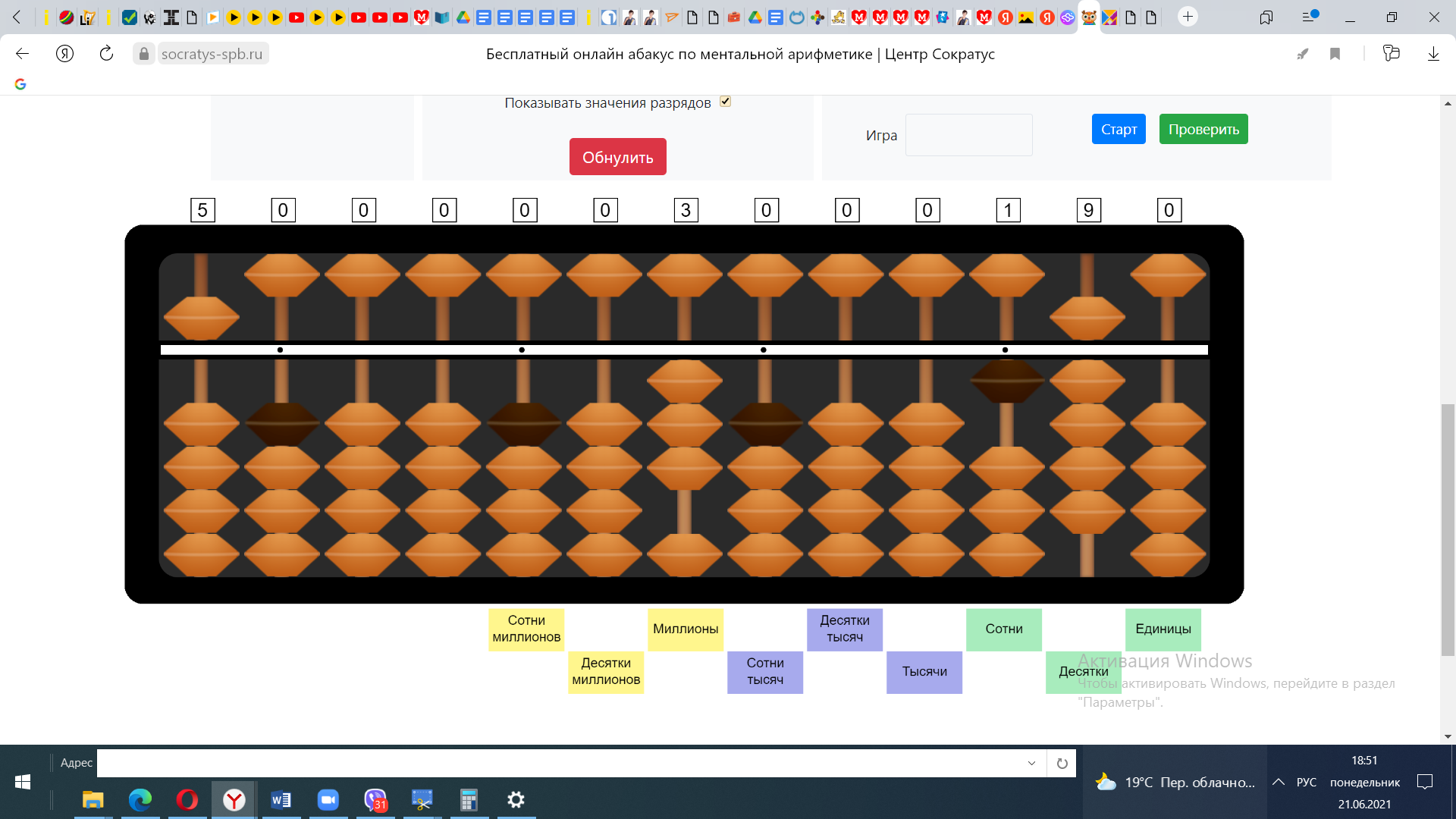
2) 3*5=15 Вычитаем 15 из 19, получаем 4.
3) Продолжаем деление. У нас получилось число 40, поделив его на 5 получим 8. Отложим число 8 в разряд единиц. Ответ 38
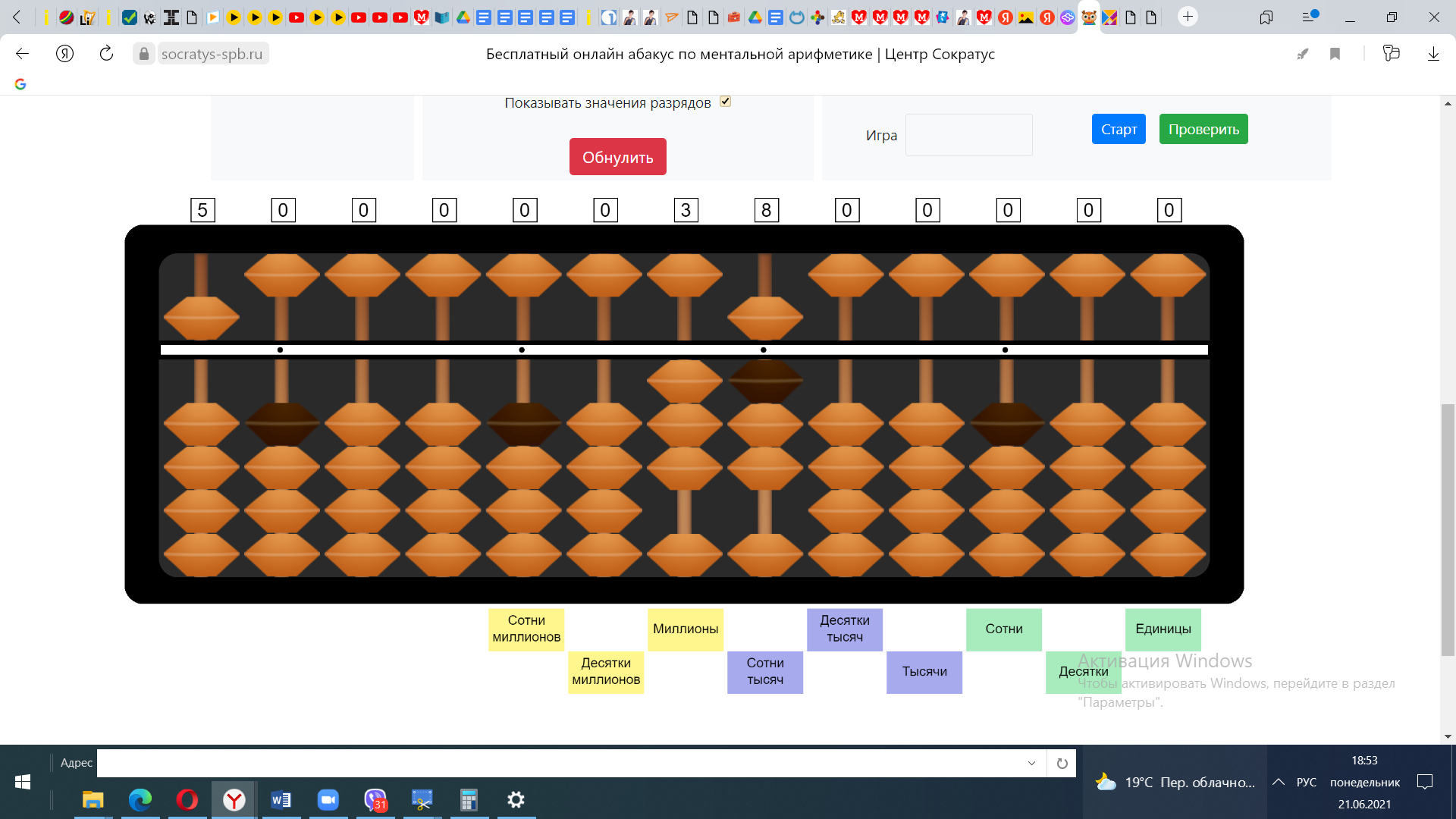
Пример №4 322:7
1) В числе 3 число 7 не убирается, поэтому берем число 32. В числе 32 число 7 убирается 4 раза. Отложим число 4 в разряде десятков.
2) 4*7=28 32-28=4
3) Продолжаем деление. У нас осталось число 42. 42:7=6. Откладываем 6 в разряд единиц. Получаем ответ 46
Деление на двузначное число, метод перебора
из книги «Японский абакус» Такаши Койима.
Пример№1 564:47
Отложим делимое и делитель привычным способом, который описан выше. В частном будет 2 цифры.
1) число старшего разряда делимого разделим на число наибольшего разряда делителя. 5:4 в числе 5 число 4 убирается 1 раз. Отложим число 1 на спице десятков. 4*1=4. Вычтем из числа 5 число 4.
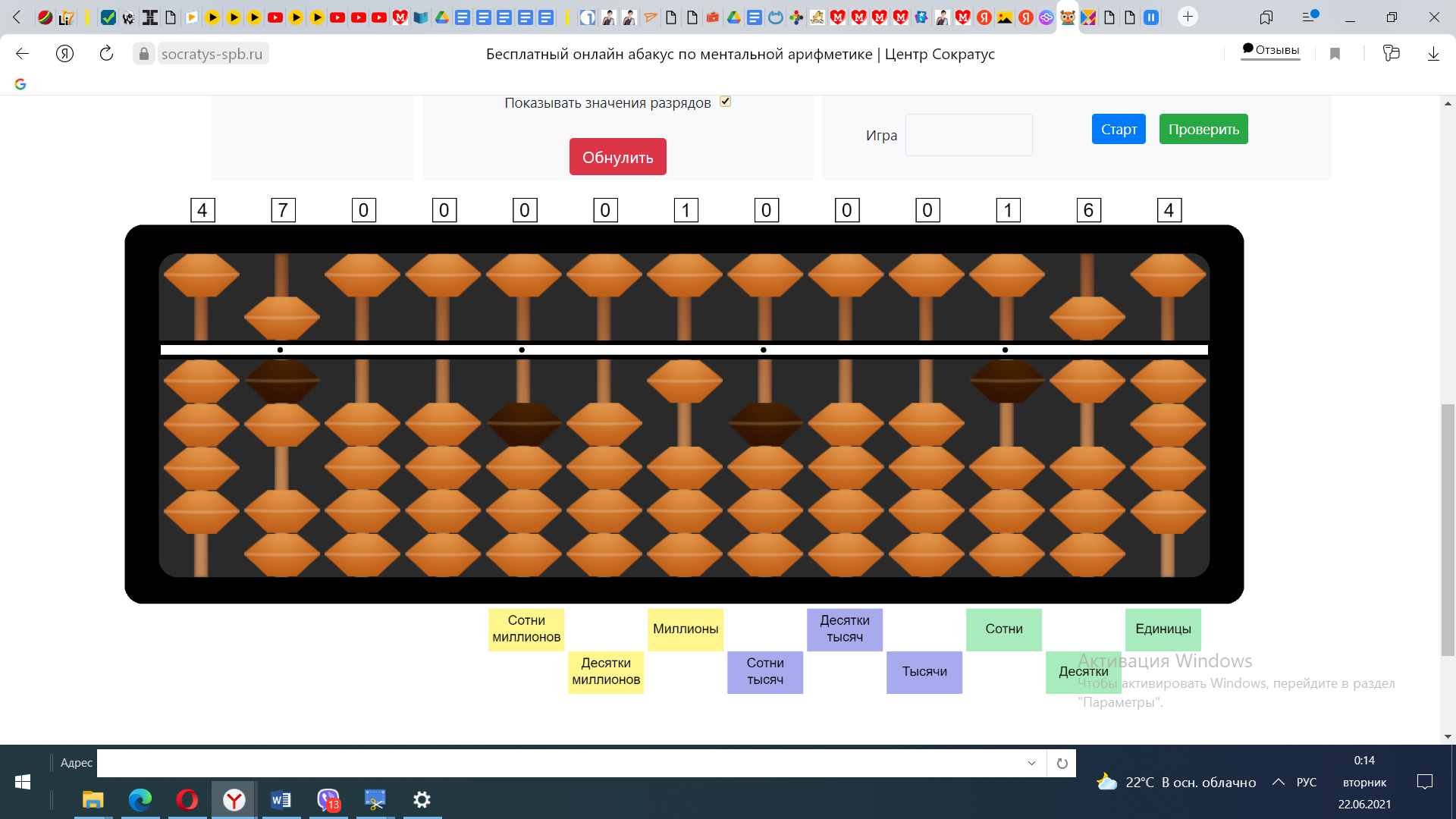
2) Выполним проверку. Для этого полученное число 1 умножим на следующий разряд делителя. 1*7=7 Из 16вычитаем 7 и получаем 9.
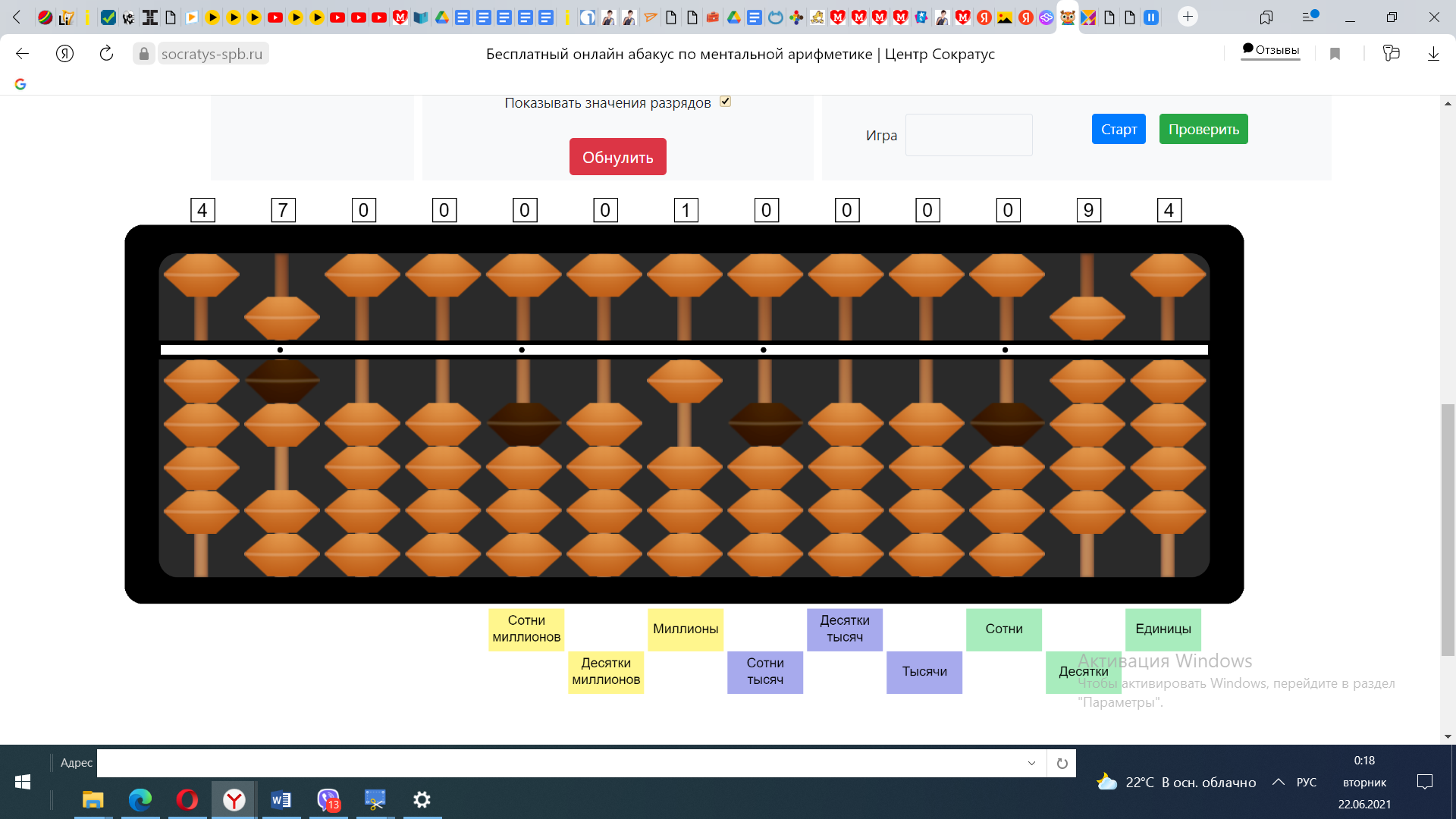
3) Продолжим вычисления. 9:4=? В числе 9 число 4 убирается 2 раза. Откладываем число 2 в частное, в разряд единиц. 2*4=8, вычитаем из числа 9 число 8, получаем 1.
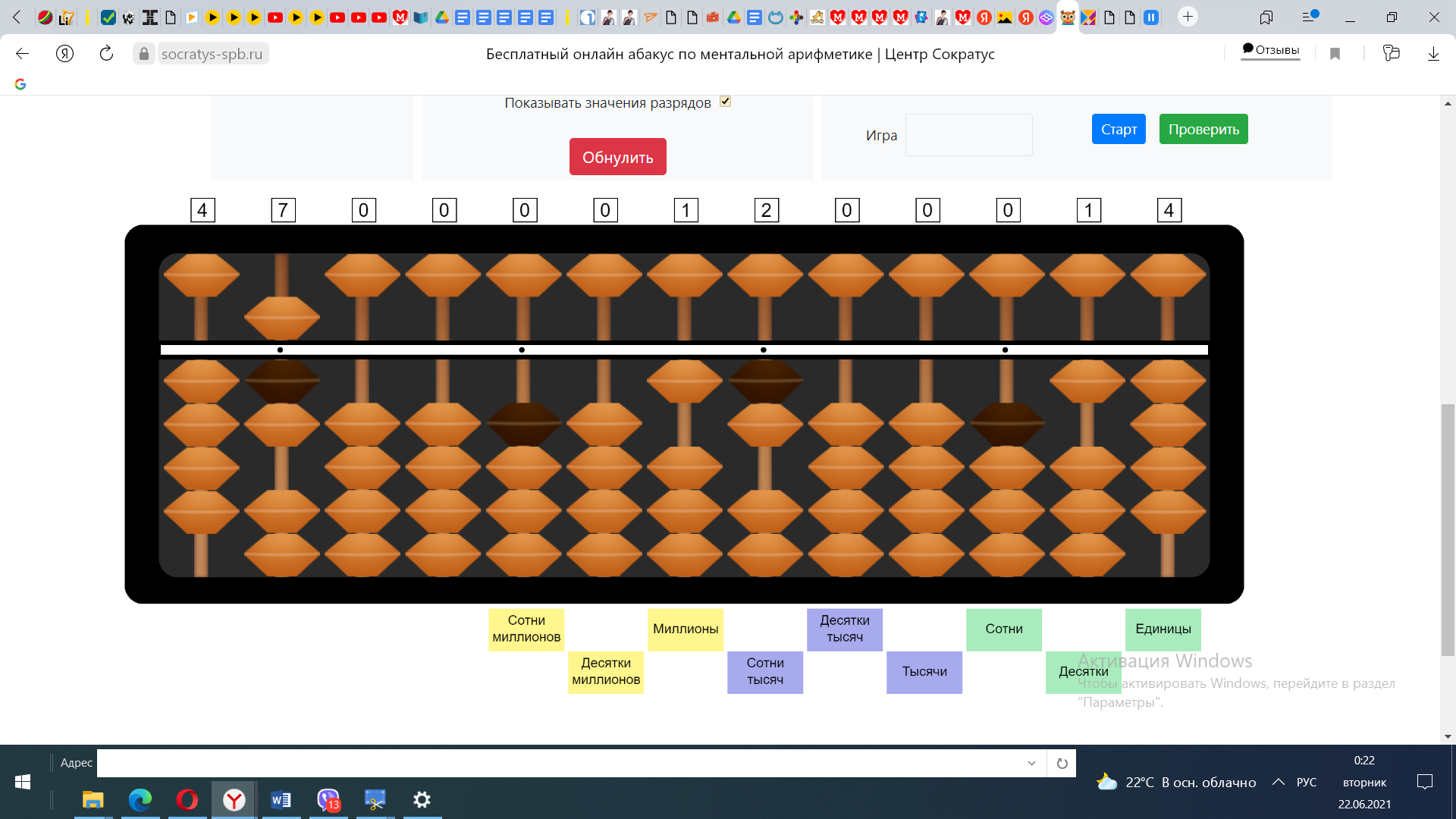
4) Теперь делаем проверку. 2*7=14. На абакусе как раз отложено 14. 14-14=0, вычисления закончены. Подобранное частное 12
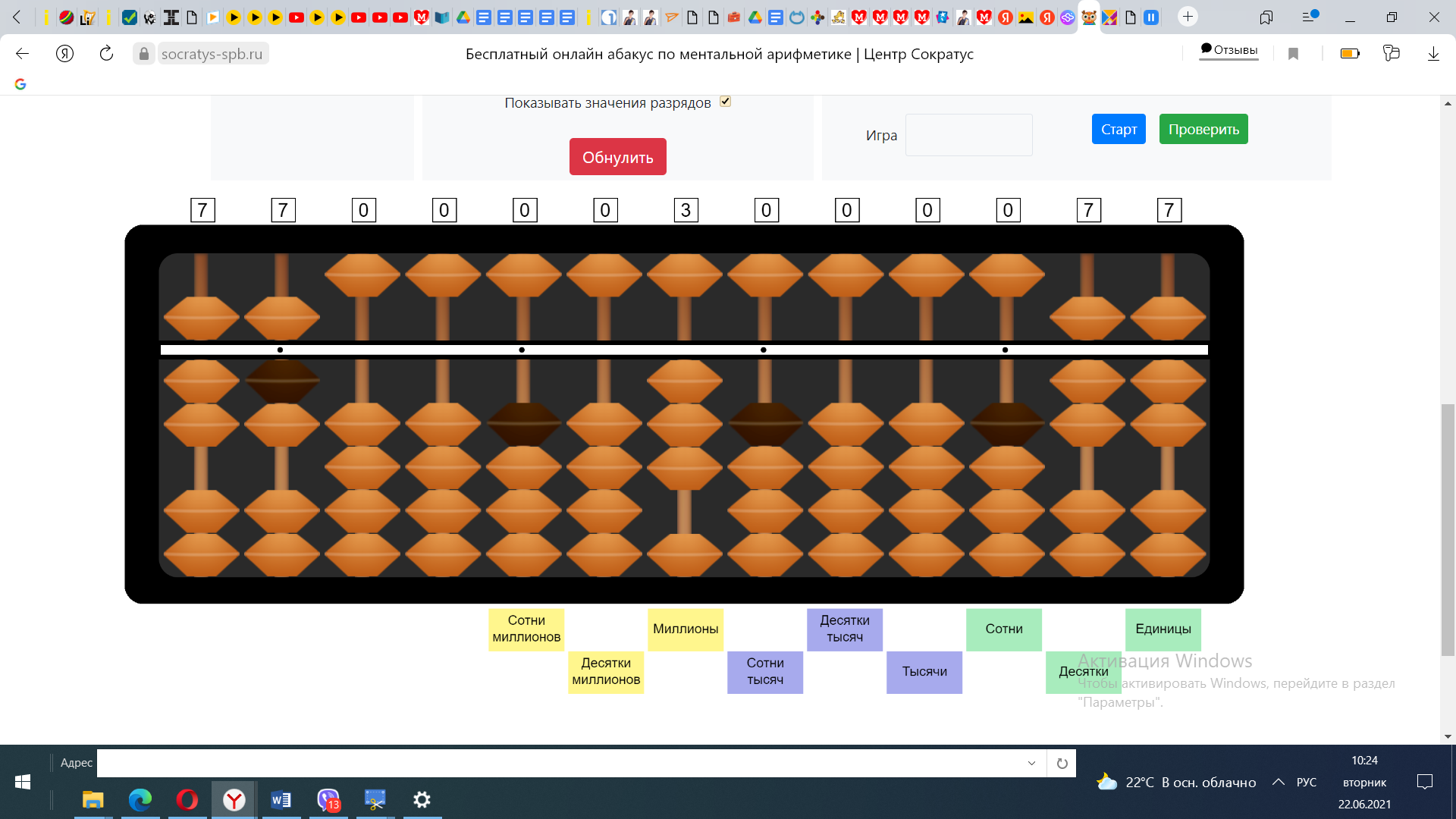
Пример№2 2387:77
Откладываем делимое и делитель, отмечаем, что в частном будет 3 цифры.
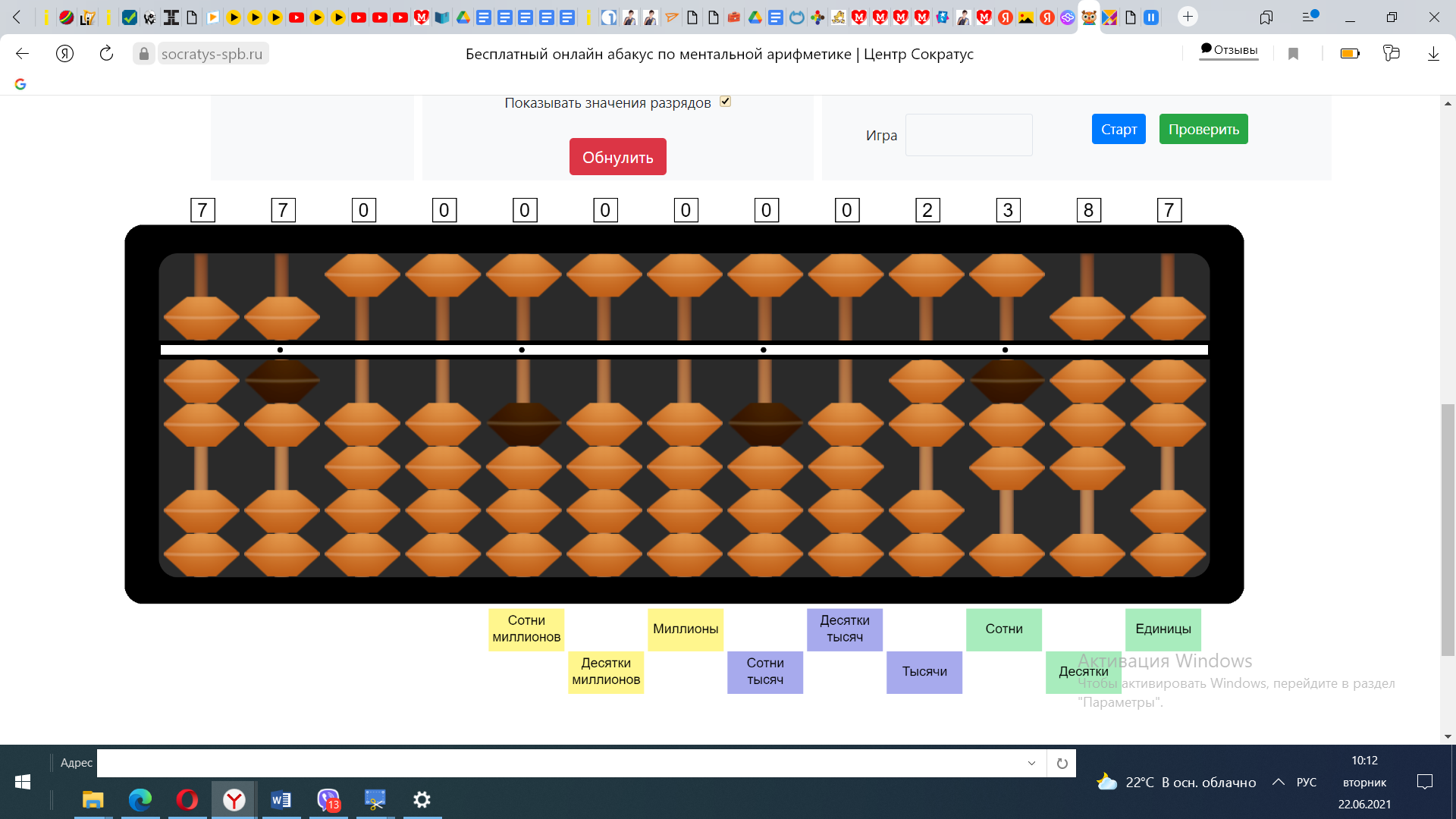
1) Разделим число наибольшего разряда делимого на число наибольшего разряда делителя. 2:7=? В числе 2 число 7 не убирается, значит берём число 23. В числе 23 число 7 убирается 3 раза. Откладываем 3 на разряде десятков в ответе. 3*7=21 Вычтем из числа 23 число 21, получим остаток 2.
2) Выполним проверку. Для этого полученное число 3 умножим на число младшего разряда делителя 3*7=21. Из числа 28-21=7 Остаток 7.
3) Продолжим вычисления. На абакусе отложено число 77. Разделим число наибольшего разряда делимого на число наибольшего разряда делителя. 7:7=1. Отложим число 1 на спице единиц в ответе. 7*1=7. Вычтем из 7 число 7. Осталось выполнить проверку.
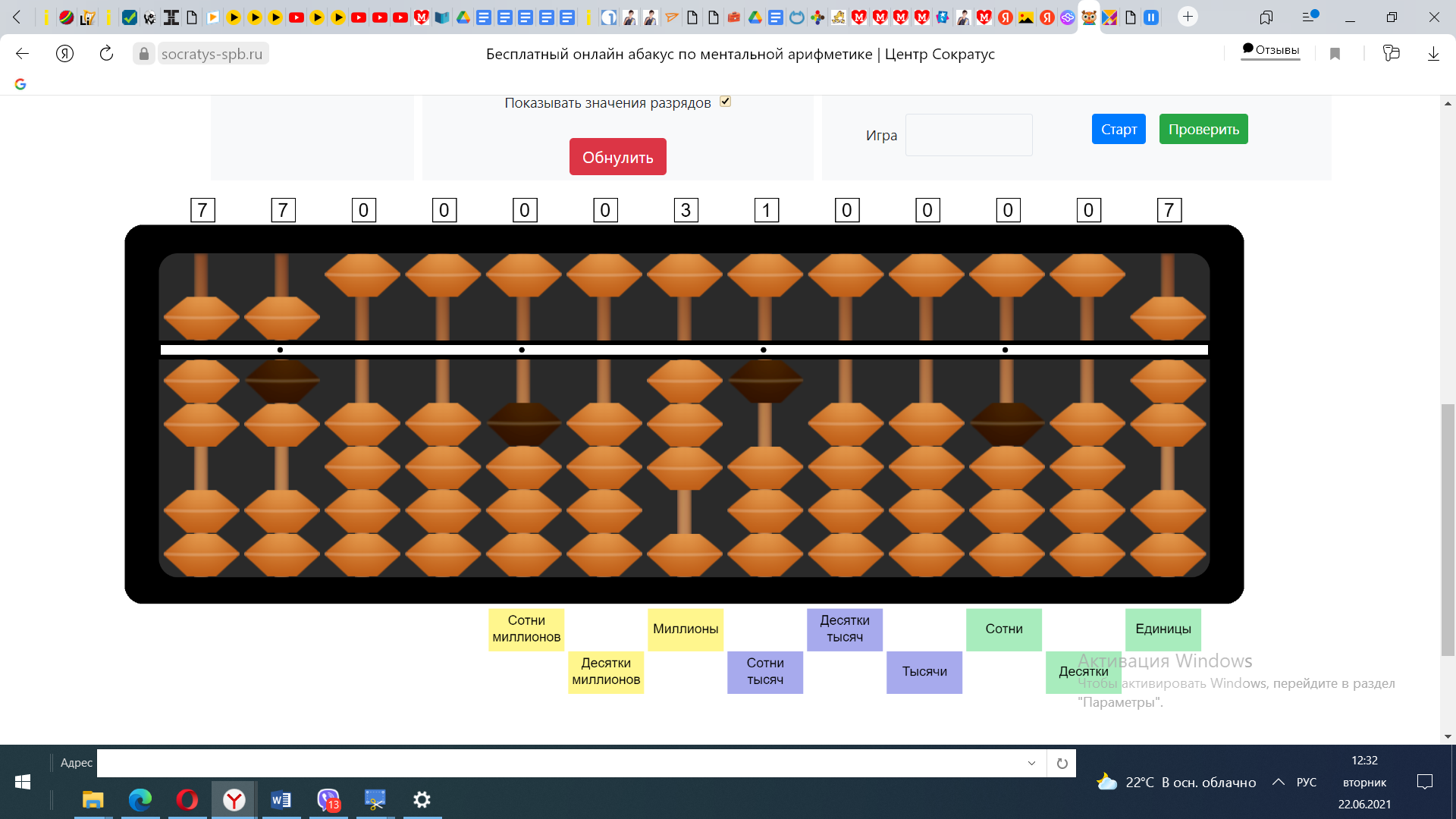
4) Выполним проверку. Полученное число 1 умножим на число меньшего разряда делителя. 1*7=7 вычтем из 7 число 7, получим 0. Подобранное частное 31
Пример№3 1218:21
Отложим делимое и делитель, определим, что частное будет состоять из 2 цифр.
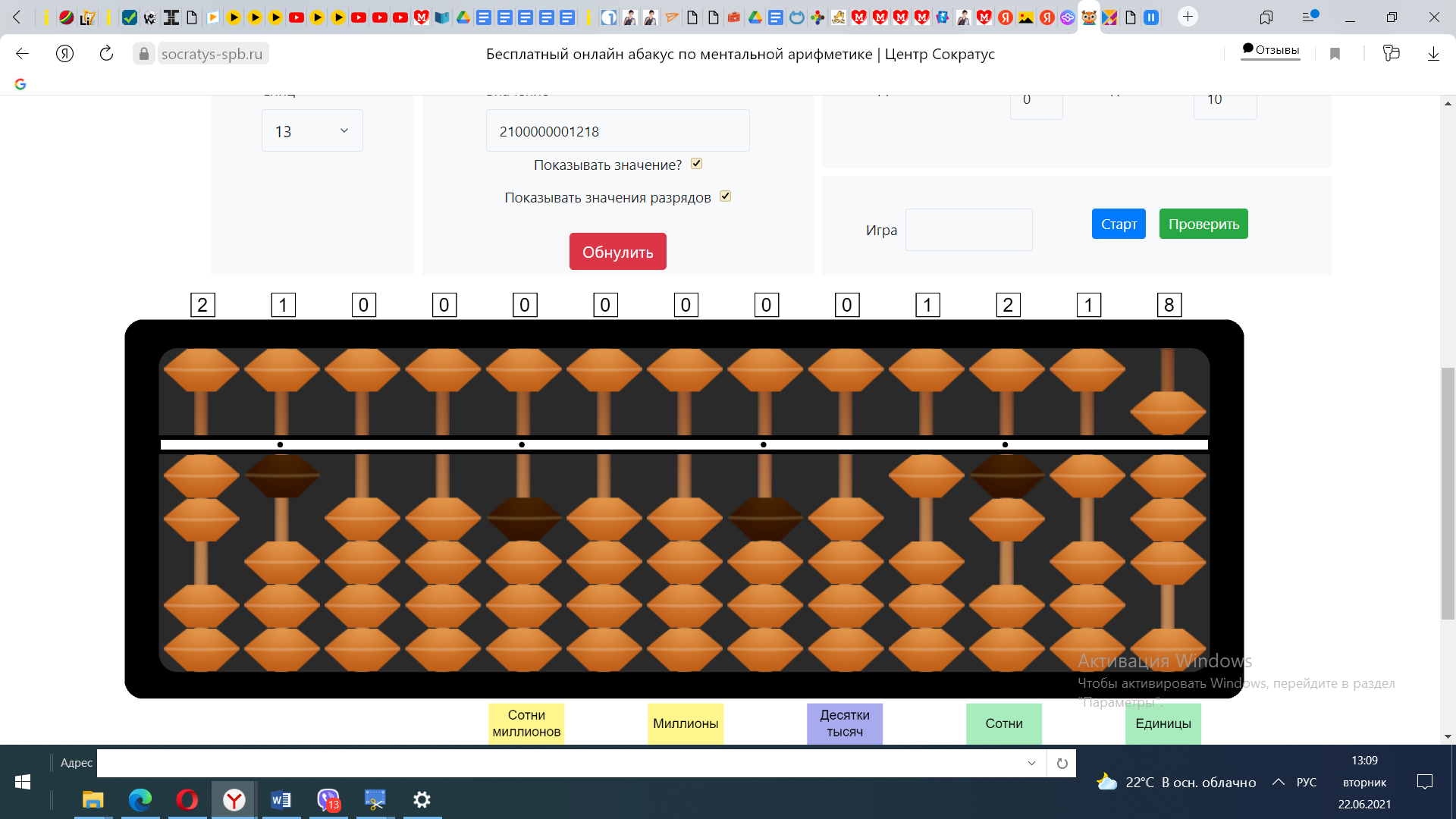
1) Разделим число наибольшего разряда делимого на число наибольшего разряда делителя. 1:2. В числе 1 число 2 не убирается, поэтому возьмём число 12. 12:2=6 Отложим на спице десятков в ответе 6. 6*2=12. Из 12 вычтем 12.
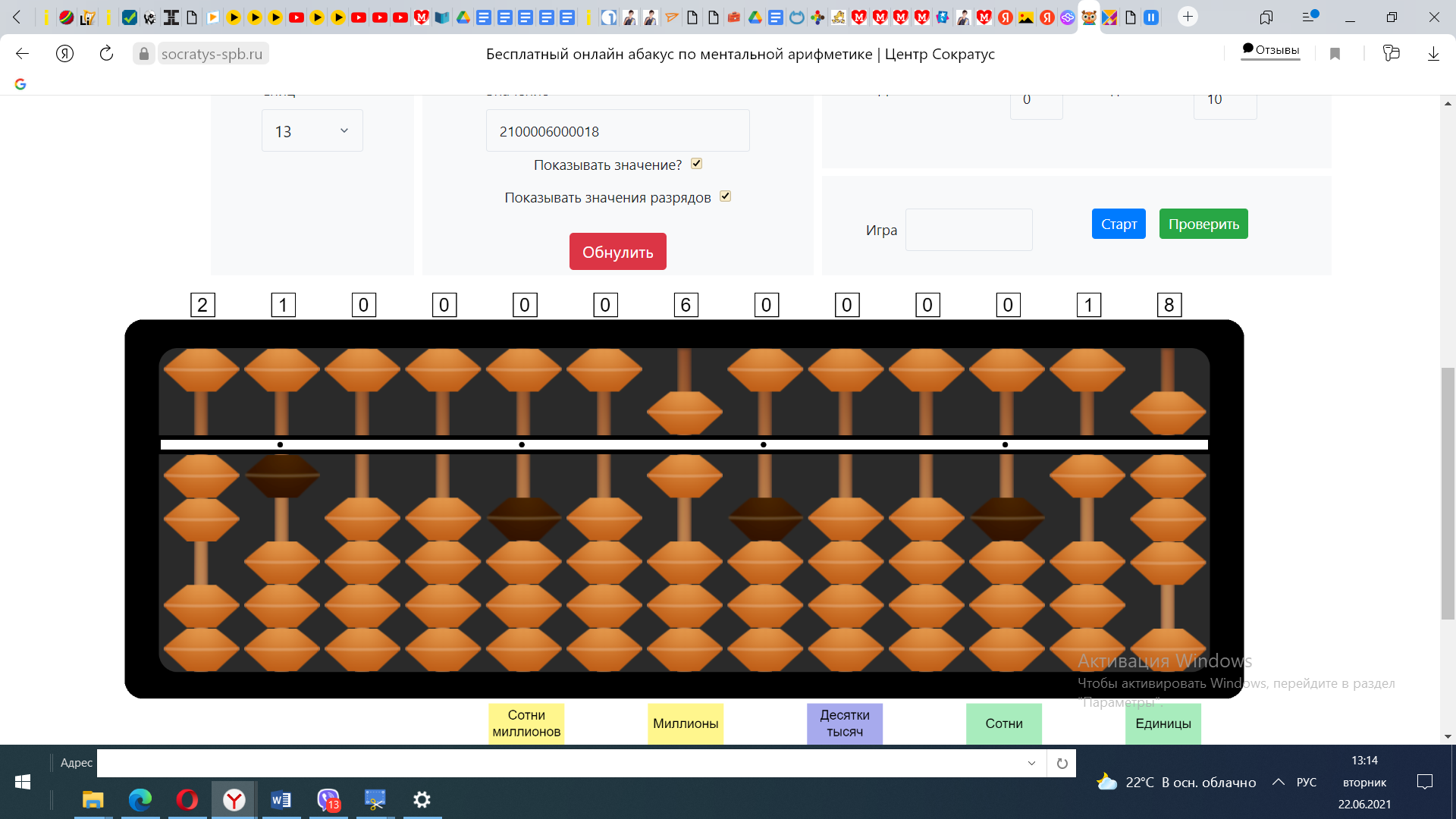
2) Выполним проверку. Полученное число 6 умножим на число меньшего разряда делителя. 6*1=6 Но у нас на абаке на спице десятков только 1. Значит мы взяли слишком большое число 6, нужно меньше. Уменьшаем будущее частное на 1, и возвращаем в разряд сотен делимого 2.
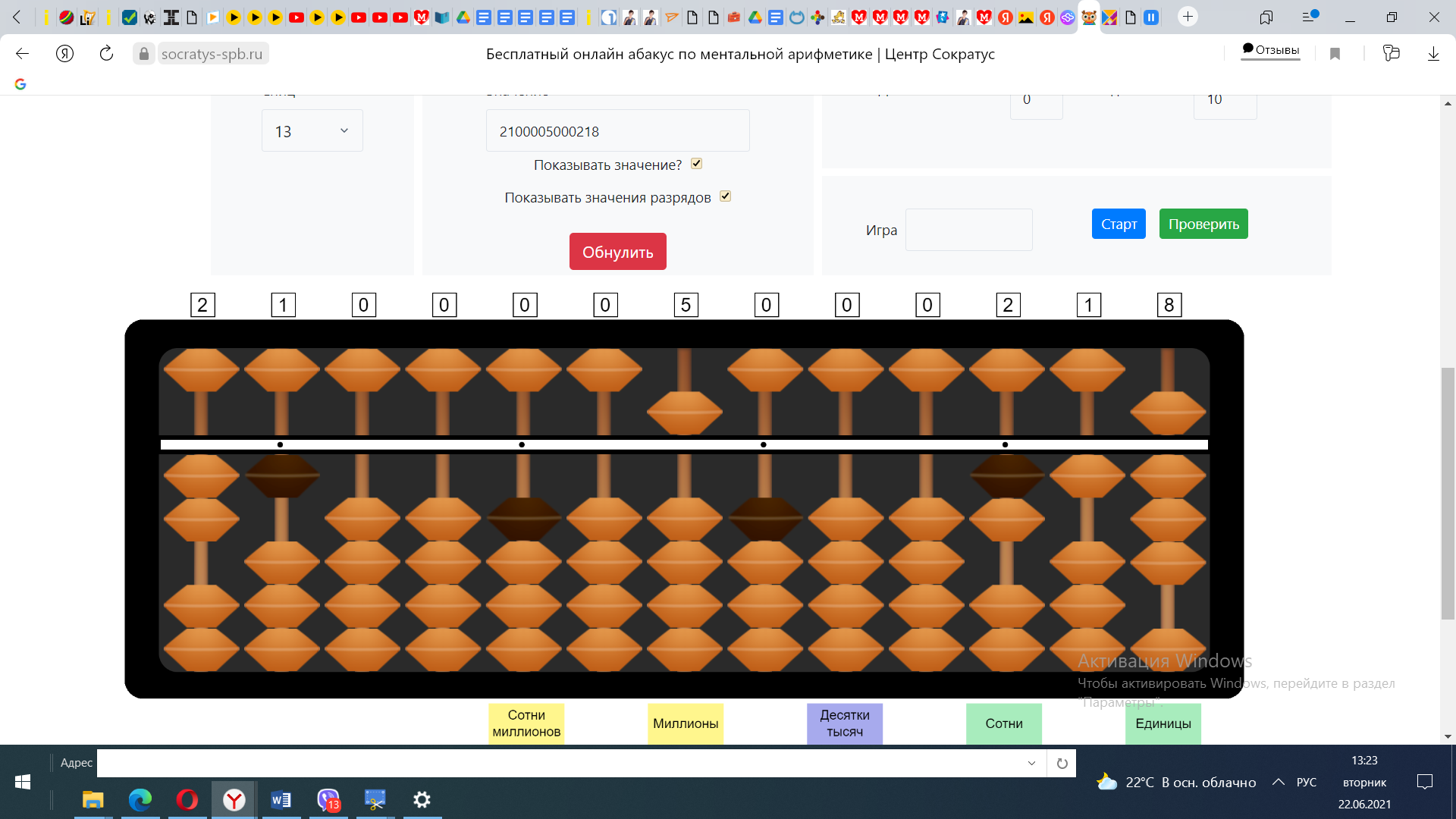
Продолжаем проверку. 5*1=5 Вычитаем 5 из 21, получаем остаток 16.
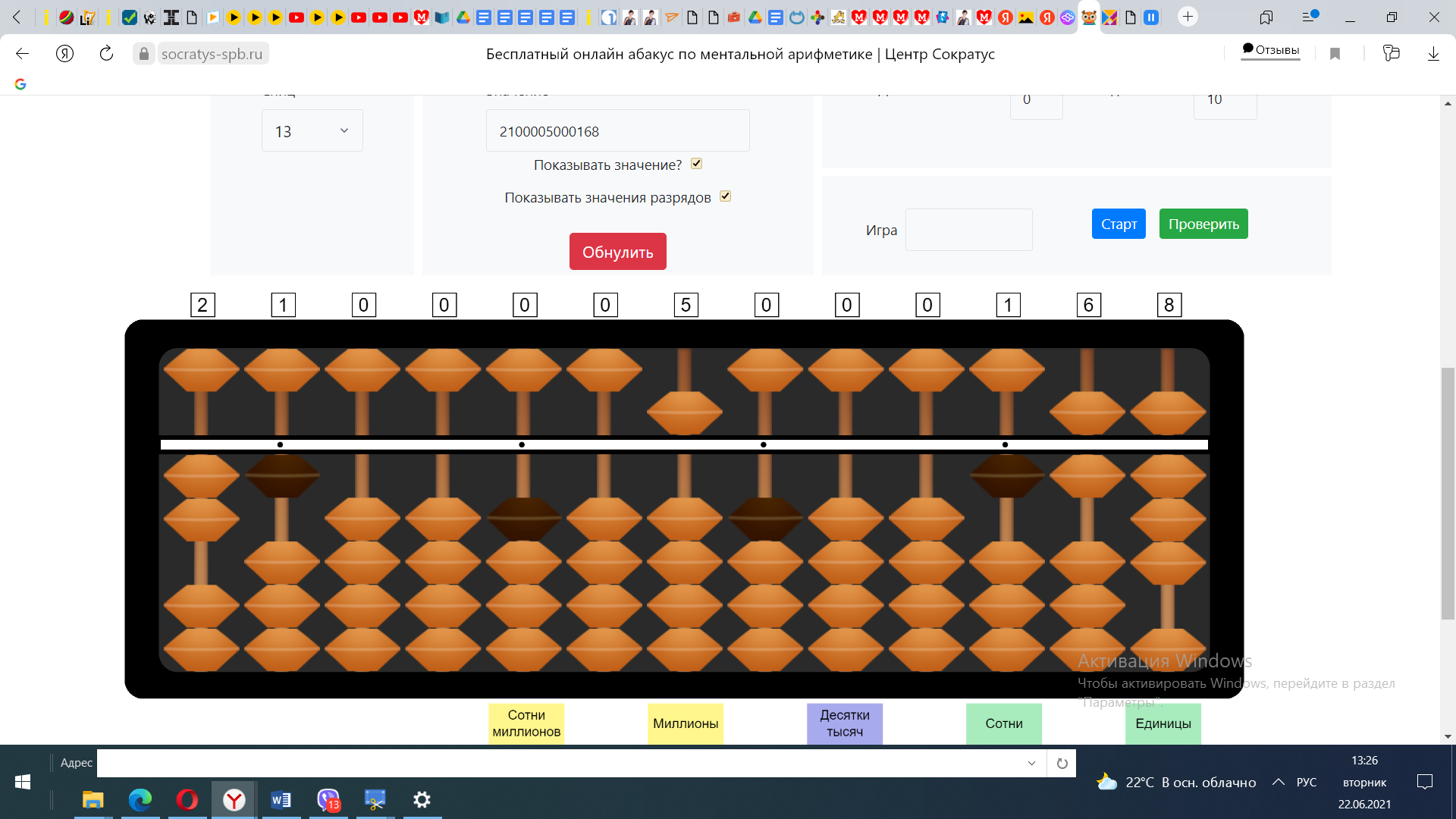
3) Продолжаем вычисления. На абакусе отложено число 168. В числе 1 число 2 не убирается, берём число 16. 16:2=8. Отложим число 8 на единицах частного. 8*2=16 из 16 вычитаем 16.
4) Выполним проверку. 8*1=8 Из8-8=0. Значит подобранное частное 58
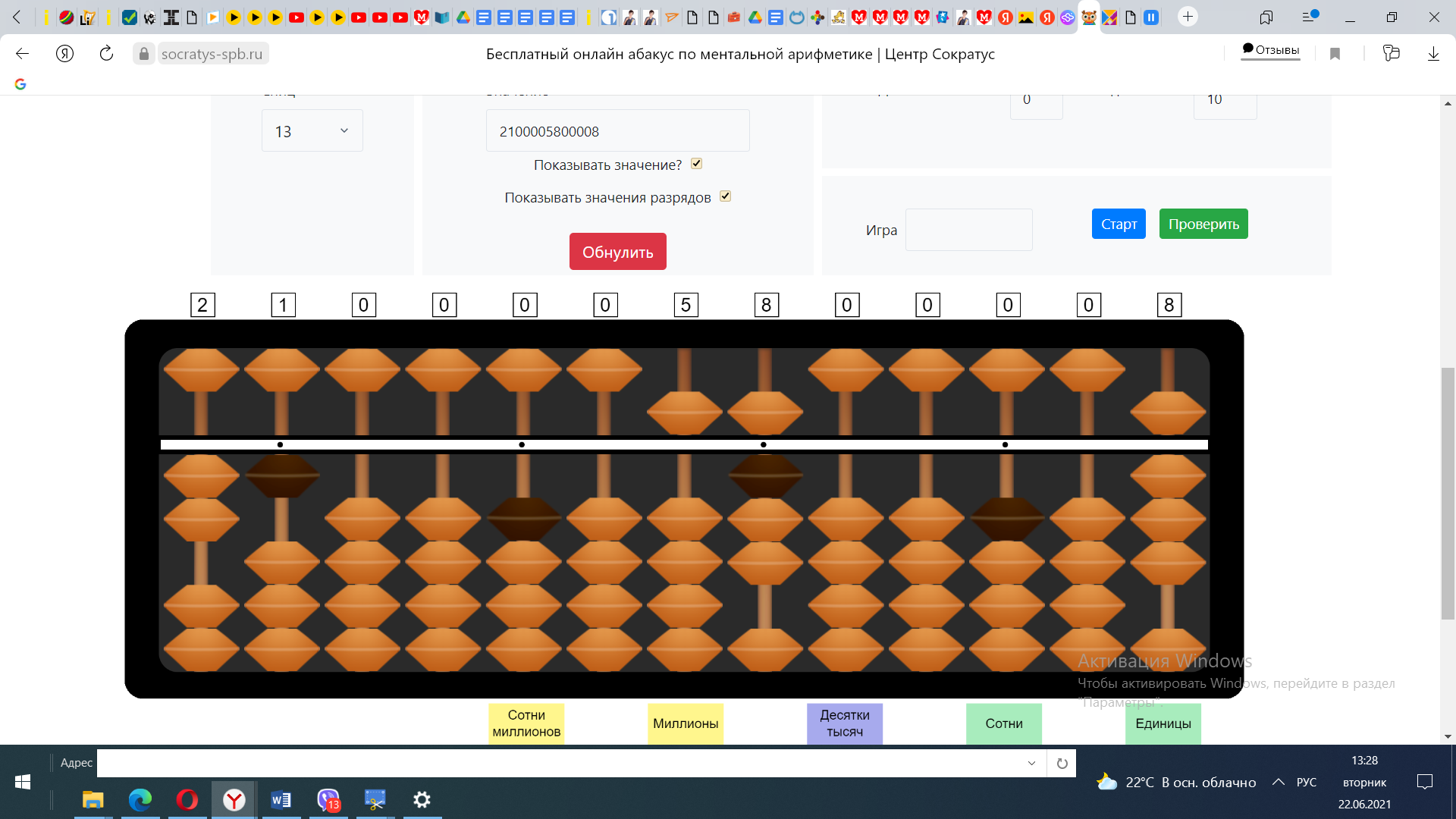
Деление с остатком
Чтобы понять, что такое остаток, нужно 10 яблок поделить между 3 детьми. Но точно разделить 10 на 3 нельзя — в результате получим по 3 яблока у каждого человека, а 1 яблоко останется неподеленным. Оно и будет остатком от деления двух чисел.
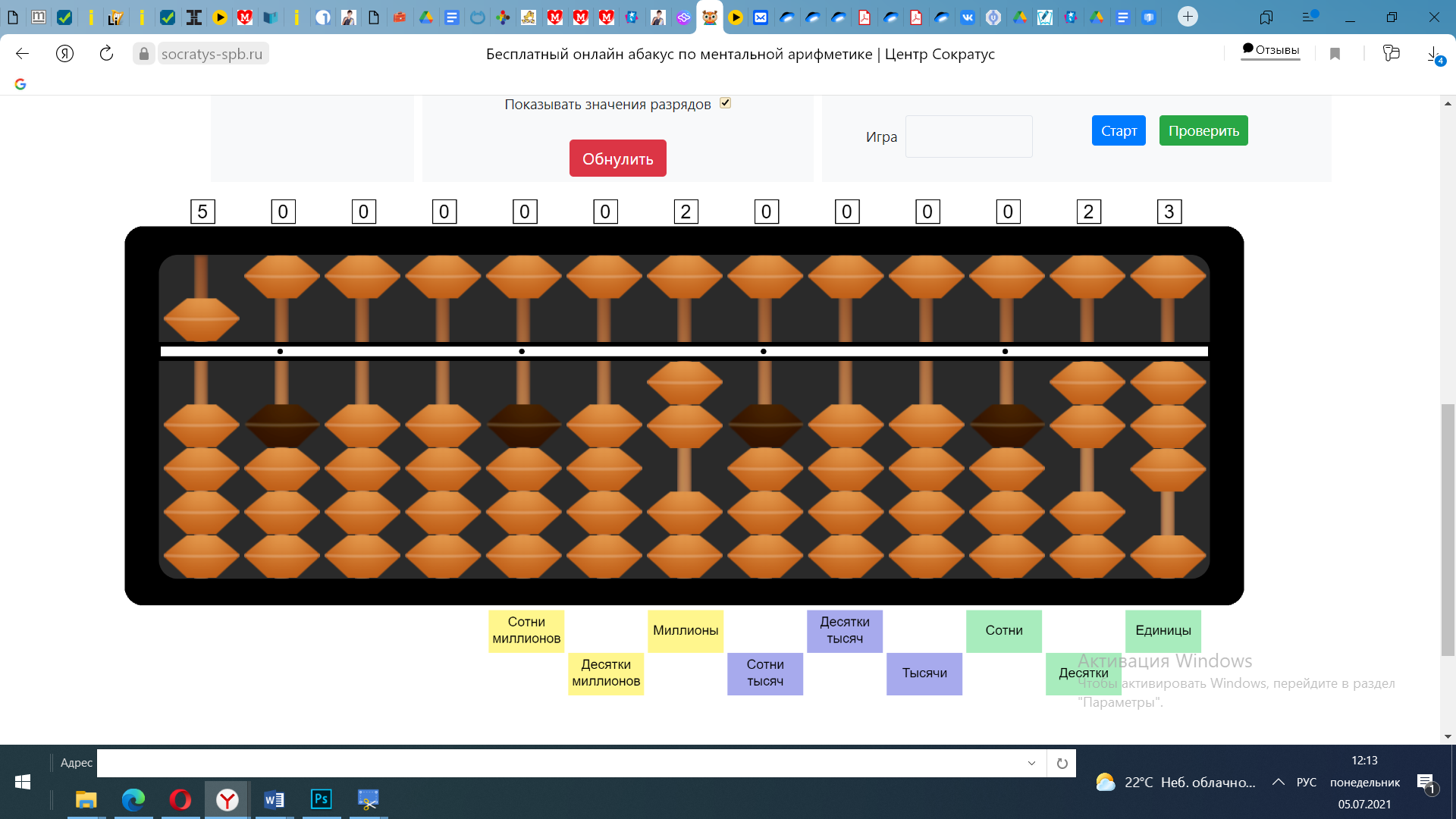
Пример: 123:5=?
По таблице делимости число 123 на 5 без остатка не делится, значит ответ будем откладывать, ориентируясь на 6 спицу, на которой будут единицы. 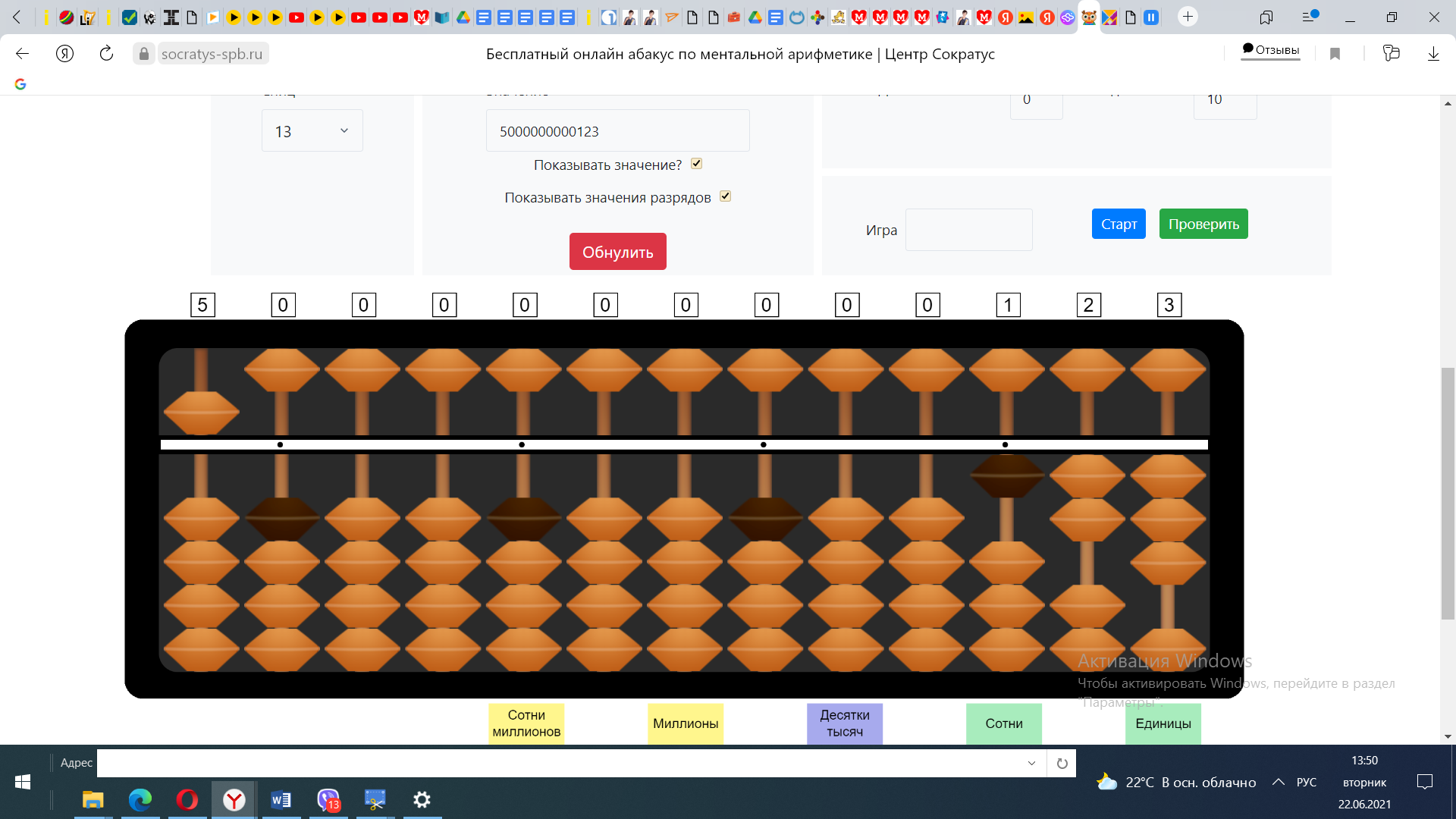
-
Определяем, что в частном будет 2 цифры
-
1 на 5 не делется, 12 на 5 не делится, но в числе 12 число 5 убирается 2 раза, откладывает 2 на спицах десятков. 2*5=10, Вычитаем число 10 из числа 12. На абакусе отложено число 23
-
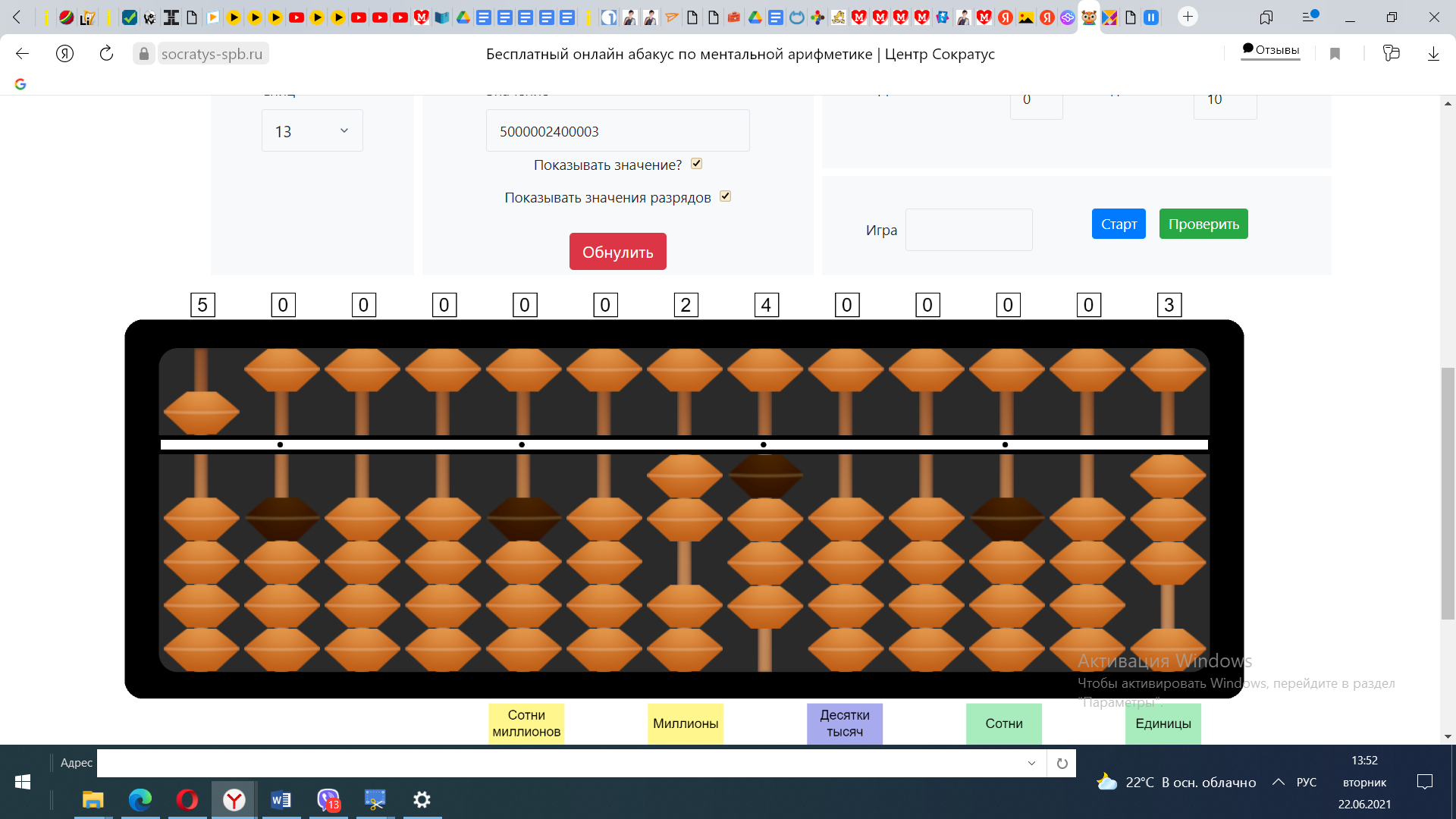
Продолжаем вычисления. 23:5 не делится, но числе 23 число 5 убирается 4 раза, откладываем число 4 на спицах единицы.
-
Получаем ответ 24 и остаток 3
-
Истомина Н.Б. Методика обучения математике в начальных классах: Учеб. пособие для студ. сред. и выс. пед. учеб. заведений. – 4 - е изд., стереотип. –М.: Издательский центр «Академия», 2001 – 288 с
-
2. Крутецкий В. А. Психология математических способностей школьников [Электронный ресурс]. URL: https://uch-lit.ru/matematika-2/dlya-studentov/krutetskiyv-a-psihologiya-matematiches (дата обращения: 04.10.2020).







































































