Самостоятельная работа обучающихся
по учебной дисциплине
МАТЕМАТИКА: АЛГЕБРА,
НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА, ГЕОМЕТРИЯ
Самостоятельная работа 1.1.Группа__________ Ф.И.______________________________________
При заполнении можно воспользоваться лекцией, учебником, ресурсами интернета:
Задание 1: заполните таблицу
|
Вид числа | Обозначение множества чисел | Примеры чисел | Для чего людям понадобились эти числа | Действия, которые можно выполнять над числами |
|
Натуральные числа |
|
|
|
|
|
Целые числа |
|
|
|
|
|
Рациональные числа |
|
|
|
|
| Иррациональные числа |
|
|
|
|
| Комплексные числа
|
|
|
|
|
Задание 2: заполните таблицу «Комплексные числа».
|
| Задание | Теоретические сведения | Пример, решение |
| 1
| Определение комплексного числа.
|
|
|
| 2 | Сложение комплексных чисел ( образец) | Суммой двух комплексных чисел а+вi и c+di называется комплексное число (а+с)+(с+d)iт.е(а+вi ) +( c+di) = (а+с)+(с+d)i | (2+3i ) +(-5+i) = (2+(-5))+(3+1)i =-3+4i
|
| 3 | Вычитание комплексных чисел.
|
|
|
| 4 | Модуль комплексного числа.
|
|
|
| 5 | Умножение комплексных чисел.
|
|
|
| 6 | Деление двух комплексных чисел.
|
|
|
| 7 | Квадратное уравнение с комплексным неизвестным.
|
|
|
Самостоятельная работа 1.2.
Форма выполнения задания: презентация.
Задание: создайте и сохраните в своей папке мультимедийную презентацию на одну из следующих тем:
Презентации должны быть выполнены с соблюдением методических рекомендаций
Методические рекомендации по составлению презентаций
Требования к презентации
На первом слайде размещается:
На втором слайде указывается содержание работы, которое лучше оформить в виде гиперссылок (для интерактивности презентации).
На последнем слайде указывается список используемой литературы в соответствии с требованиями, интернет-ресурсы указываются в последнюю очередь.
| Оформление слайдов |
| Стиль | необходимо соблюдать единый стиль оформления; нужно избегать стилей, которые будут отвлекать от самой презентации; вспомогательная информация (управляющие кнопки) не должны преобладать над основной информацией (текст, рисунки). |
| Фон | |
| Использование цвета | на одном слайде рекомендуется использовать не более трех цветов: один для фона, один для заголовков, один для текста; для фона и текста используются контрастные цвета; особое внимание следует обратить на цвет гиперссылок (до и после использования). |
| Анимационные эффекты | нужно использовать возможности компьютерной анимации для представления информации на слайде; не стоит злоупотреблять различными анимационными эффектами; анимационные эффекты не должны отвлекать внимание от содержания информации на слайде. |
| Представление информации |
| Содержание информации | следует использовать короткие слова и предложения; время глаголов должно быть везде одинаковым; следует использовать минимум предлогов, наречий, прилагательных; заголовки должны привлекать внимание аудитории. |
| Расположение информации на странице | предпочтительно горизонтальное расположение информации; наиболее важная информация должна располагаться в центре экрана; если на слайде располагается картинка, надпись должна располагаться под ней. |
| Шрифты | для заголовков не менее 24; для остальной информации не менее 18; шрифты без засечек легче читать с большого расстояния; нельзя смешивать разные типы шрифтов в одной презентации; для выделения информации следует использовать жирный шрифт, курсив или подчеркивание того же типа; нельзя злоупотреблять прописными буквами (они читаются хуже, чем строчные). |
| Способы выделения информации | Следует использовать: рамки, границы, заливку; разные цвета шрифтов, штриховку, стрелки; рисунки, диаграммы, схемы для иллюстрации наиболее важных фактов. |
| Объем информации | не стоит заполнять один слайд слишком большим объемом информации: люди могут единовременно запомнить не более трех фактов, выводов, определений; наибольшая эффективность достигается тогда, когда ключевые пункты отражаются по одному на каждом отдельном слайде. |
| Виды слайдов | Для обеспечения разнообразия следует использовать разные виды слайдов: с текстом, с таблицами, с диаграммами. |
Самостоятельная работа 2.1. Группа______ Ф.И.__________________________________________
Задание 1. Составить карточку- консультацию, таблицу (краткий справочный материал, примеры решения типовых заданий, задания для самостоятельной работы) Тема:« Корни »
| Краткий справочный материал по теме | Примеры решения типовых заданий | Задания для самостоятельной работы |
| 
Читаем: «Корень n-ой степени из числа а» |
 - читаем: корень 3-ей степени из 2-х; - читаем: корень 3-ей степени из 2-х;
 - читаем: корень 5-ой степени из с - читаем: корень 5-ой степени из с
|
Прочитайте:  , ,  |
|  = bbn = a = bbn = a
|  = 2 23 = 8 = 2 23 = 8
 = 3 34 = 81 = 3 34 = 81
 = =  = 5 52 = 25 = 5 52 = 25
 = -3 (-3)3 = -27 = -3 (-3)3 = -27
 = =  ( (  )5 = )5 = 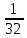
| Вычислите: 1) = = 2) = = 3) = = 4) = = |
|  ∙ ∙ = = 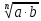
|  ∙ ∙  = =  = = = 3 = 3
 ∙ ∙  = =  = =  = -3 = -3
| Вычислите: 1) ∙ ∙  ; ; 2) ∙ ∙  |
|  = =
в ≠ 0 |  = = = = = 2 = 2
| Вычислите: 1) ; ; 2) 3) ; ; |
|  = =  k k
к 0 |  = =  2 = 2 =  = 2 = 2
| Измените степень корня; найдите значение подкоренного выражения: 1) = = 
2) = =  |
|  k = ( k = ( )k )k
Если k ≤ 0, то а≠ 0 |  2 = ( 2 = ( )2 = 42 = 16 )2 = 42 = 16
 3 = ( 3 = ( )3 = 33 = 27 )3 = 33 = 27
| Вычислите: 1) 4= 4= 2) 2= 2= 3) 3= 3= |
|  n = an/m n = an/m
m 0 |  8 = 28/4 = 22 = 4 8 = 28/4 = 22 = 4
 3 = 63/3 = 6 3 = 63/3 = 6
| Вычислите: 1) 12= 12= 2) 7= 7= |
Самостоятельная работа 2.2. Группа______ Ф.И._______________________________________
Форма выполнения задания: таблица.
Заполнить таблицу «Корни, степени и логарифмы».
При заполнении можно воспользоваться лекциями, учебниками, ресурсами интернета:
|
| Понятия | Теоретические сведения | Пример, решение |
| 1
| Определение степени.
|
|
|
| 2 | Свойства степени с действительным показателем.
|
|
|
| 3 | Определение арифметического корня.
|
|
|
| 4 | Свойства арифметического корня.
|
|
|
| 5 | Определение логарифма.
|
|
|
| 6 | Основное логарифмическое тождество.
|
|
|
| 7 | Условие существования логарифма.
|
|
|
| 8 | Свойства логарифмов.
|
|
|
Самостоятельная работа 2.3.
Форма выполнения задания: кроссворд.
Задание: составить кроссворд «Степени, корни, логарифмы», с соблюдением методических рекомендаций по составлению кроссвордов.
Методические рекомендации по составлению кроссвордов
В процессе работы обучающиеся:
просматривают и изучают необходимый материал, как в лекциях, так и в дополнительных источниках информации;
составляют список слов раздельно по направлениям;
составляют вопросы к отобранным словам;
проверяют орфографию текста, соответствие нумерации;
оформляют готовый кроссворд.
Общие требования при составлении кроссвордов:
не допускается наличие "плашек" (незаполненных клеток) в сетке кроссворда;
не допускаются случайные буквосочетания и пересечения;
загаданные слова должны быть именами существительными в именительном падеже единственного числа;
двухбуквенные слова должны иметь два пересечения;
трехбуквенные слова должны иметь не менее двух пересечений;
не допускаются аббревиатуры (ЗиЛ и т.д.), сокращения (детдом и др.);
не рекомендуется большое количество двухбуквенных слов;
все тексты должны быть написаны разборчиво, желательно отпечатаны.
Требования к оформлению:
на каждом листе должна быть фамилия автора, а также название данного кроссворда;
рисунок кроссворда должен быть четким;
сетки всех кроссвордов должны быть выполнены в двух экземплярах:
1-й экз. - с заполненными словами;
2-й экз. - только с цифрами позиций.
Ответы публикуются отдельно. Ответы предназначены для проверки правильности решения кроссворда и дают возможность ознакомиться с правильными ответами на нерешенные позиции условий, что способствует решению одной из основных задач разгадывания кроссвордов — повышению эрудиции и увеличению словарного запаса.
Критерии оценивания составленных кроссвордов:
Четкость изложения материала, полнота исследования темы.
Оригинальность составления кроссворда.
Практическая значимость работы.
Уровень стилевого изложения материала, отсутствие стилистических ошибок.
Уровень оформления работы, наличие или отсутствие грамматических и пунктуационных ошибок.
Количество вопросов в кроссворде, правильное их изложения.
Самостоятельная работа 2.4. Группа________Ф.И.__________________________________
Форма выполнения задания: вычисление логарифмов.
Задание: вычислить логарифмы.
| Вариант 1 Вычислить:
1. log4 16=
2. log25 125=
3. log8 2=
4. log 49= 49=
5. log 6 = =
6. 32log37=
7. log  = =
8. log9 = =
9. Найдите х, если =
| Вариант 2 Вычислить:
1. log3 27=
2. log49 7=
3. log4 8=
4. log 3= 3=
5. log 5
6. 27log32
7. log 9 9
8. log  
9. Найдите х, если

|
Самостоятельная работа 3.1. Группа_______ Ф.И._____________________________________
Форма выполнения задания: оформленная таблица.
Заполнить таблицу «Прямые и плоскости в пространстве».
При заполнении можно воспользоваться лекциями, учебниками, ресурсами интернета:
|
| Закончить предложения или ответить на вопросы: |
| чертежи |
| 1
| Аксиомы стереометрии: | 1)
2)
3)
|
|
| 2 | Существует 3 случая расположения прямых в пространстве: | 1)
2)
3)
|
|
| 3 | Две прямые в пространстве параллельны, если…
|
|
|
| 4 | Две прямые пересекаются, если…
|
|
|
| 5 | Две прямые скрещиваются, если…
|
|
|
| 6 | Признак скрещивающихся прямых:
|
|
|
| 7 | Существует 3 случая расположения прямой и плоскости: | 1)
2)
3)
|
|
| 8 | Прямая и плоскость пересекаются,, если..
|
|
|
| 9 | Прямая и плоскость параллельны, если…
|
|
|
| 10 | Прямая лежит в плоскости, если…
|
|
|
| 11 | Признак параллельности прямой и плоскости:
|
|
|
| 12 | Существует 2 случая расположения двух плоскостей: | 1)
2)
|
|
| 13 | Плоскости пересекаются, если…
|
|
|
| 14 | Плоскости параллельны, если…
|
|
|
| 15 | Признак параллельности двух плоскостей:
|
|
|
| 16 | Свойства параллельных плоскостей:
| 1)
2)
|
|
| 17 | Две прямые в пространстве перпендикулярны, если…
|
|
|
| 18 | Прямая и плоскость перпендикулярны, если…
|
|
|
| 19 | Признак перпендикулярности прямой и плоскости:
|
|
|
| 20 | Признак перпендикулярности двух плоскостей:
|
|
|
| 21 | Две плоскости перпендикулярны, если…
|
|
|
| 22 | Сформулируйте понятия: Перпендикуляр – это…
Наклонная – это…
Проекция – это…
|
|
|
| 23 | Теорема о трех перпендикулярах:
|
|
|
| 24 | Угол между прямой и плоскостью это…
|
|
|
| 25 | Двугранный угол – это…
|
|
|
Самостоятельная работа 3.2.
Форма выполнения задания: кроссворд.
Задание: составить кроссворд на тему «Взаимное расположение прямых и плоскостей в пространстве» ,с соблюдением методических рекомендаций по составлению кроссвордов.
Кроссворд-это игра, состоящая в разгадывании слов по определениям.
Методические рекомендации( смотреть мед.рек. по оформлению С/Р 2.3.)
Образец оформления и составления кроссвордов
| По горизонтали:
1. Сторона прямоугольного треугольника. 4. Он есть у функции и последовательности. 8. Его штаны равны во все стороны. 10. Полный круг вращения. 13. Французский математик, специалист теории вероятностей. 14. Арифметическое действие. 16. Гектар — ... площади. 17. Часть матрицы. 18. Свойство углов. 19. Полупрямая. 22. Нейтральный элемент относительно умножения. 23. Группа повторяющихся цифр в бесконечной десятичной дроби. 24. Наибольший общий ...
| По вертикали:
2. Бублик как математический объект. 3. Положение, нуждающееся в доказательстве. 4. Поверхность, имеющая 2 измерения. 5. Линейное алгебраическое уравнение. 6. Тригонометрическая функция. 7. Один из двух экстремумов. 9. Функция по своей сути. 11. Часть прямой. 12. Линия. 15. Геометрическая фигура, образованная двумя лучами. 17. Полный квадрат первого двузначного числа. 18. Для него необходимы натуральные числа. 20. В теории графов: маршрут, все ребра которого различны. 21. В теории графов: замкнутый маршрут, все ребра которого различны.
|
Ответы:
| По горизонтали: 1-катет; 4-предел; 8-пифагор; 10-оборот; 13-пуассон; 14-умножение; 16-мера; 17-строка; 18-смежность; 19-луч; 22-единица; 23-период; 24-делитель;
| По вертикали: 2-тор; 3-теорема; 4-плоскость; 5-лау; 8-синус; 7-максимум; 9-отображение; 11-отрезок; 12-кривая; 15-угол; 17-сто; 18-счёт; 20-цепь; 21-цикл.
|
Самостоятельная работа 4.1.
Форма самостоятельной деятельности: подготовить сообщение по предложенной теме.
Методические рекомендации
Сообщение должно соответствовать методическим рекомендациям по подготовке сообщений.
Самостоятельная работа 4.2.
Форма самостоятельной деятельности: Составить, подобрать комбинаторные задачи в дополнительной литературе и сети интернет
Самостоятельная работа 5.1. Группа_______ Ф.И.___________________________________
Форма выполнения задания: оформленная таблица.
Заполнить таблицу «Координаты и векторы».
При заполнении можно воспользоваться лекциями, учебниками, ресурсами интернета:
|
| Понятия | Теоретические сведения, формулы | Пример, решение |
| 1 | Понятие вектора
|
|
|
| 2 | Правила действий над векторами
|
|
|
| 3 | Компланарные векторы
|
|
|
| 4 | Координаты точки и координаты вектора в пространстве.
|
|
|
| 5 | Скалярное произведение векторов.
|
|
|
| 6 | Угол между векторами
|
|
|
Самостоятельная работа 5.2. Группа_______Ф.И.__________________________________________
Форма выполнения задания: решение контрольной работы по вариантам.
Задание: выполнить домашнюю контрольную работу «Векторы».
| Вариант 1 1. От точки А отложите вектор: а) равный  ; б) сонаправленный ; б) сонаправленный ; в) противоположно направленный ; в) противоположно направленный  . . 
2. ABCD – ромб. Равны ли векторы: а)  ____; б) ____; б)  ____; ____; в)  ____. ____.
3. Начертите два неколлинеарных вектора  и и  . . Постройте вектор  . .
4. В параллелограмме АВСD на стороне АВ отмечена точка К так, что АК: КВ=2:1, О – точка пересечения диагоналей. Выразите векторы  и и  через векторы через векторы  и и  . .
5. Чему равны координаты вектора  1)  2) 2)  3) 3) 
6. Запишите разложение вектора  по координатным векторам по координатным векторам  и и  . ___________ . ___________
7. Даны два вектора  : : 1) найдите координаты вектора  ______ ______
2) будут ли коллинеарными векторы  и и  _______ _______ 8. Найдите координаты вектора  , если , если  . __________________ . __________________
| Вариант 2 1. От точки В отложите вектор: а) равный  ; б) сонаправленный ; б) сонаправленный ;в) противоположно направленный ;в) противоположно направленный  . . 
2. ABCD – квадрат. Равны ли векторы: а)  ____; б) ____; б)  _____; в) _____; в)  ____. ____.
3. Начертите два неколлинеарных вектора  и и  . . Постройте вектор  . .
4. В параллелограмме АВСD на стороне ВС отмечена точка Р так, что ВР:РС=3:1, О – точка пересечения диагоналей. Выразите векторы  и и  через векторы через векторы  и и  . .
5. Чему равны координаты вектора  1)  2) 2)  3) 3) 
6. Запишите разложение вектора  по координатным векторам по координатным векторам  и и  . ___________ . ___________
7. Даны два вектора  : : 1) найдите координаты вектора  ______ ______ 2) будут ли коллинеарными векторы  и и  _______ _______
8. Найдите координаты вектора  , если , если  . __________________ . __________________
|
Самостоятельная работа 6.1. Группа______ Ф.И.______________________________________
Форма выполнения задания: оформленная таблица.
Заполнить таблицу «Тригонометрия. Теория и практика».
При заполнении можно воспользоваться лекциями, учебниками, ресурсами интернета:
|
| Понятия | Теоретические сведения, формулы | Пример, решение |
| 1
| Основное тригонометрическое тождество
|
|
|
| 2 | Зависимость между синусом, косинусом, тангенсом и котангенсом.
|
|
|
| 3 | Знаки тригонометрических функций
|
|
|
| 4 | Формулы двойного угла
|
|
|
| 5 | Формулы сложения
|
|
|
| 6 | Формулы преобразования суммы и разности в произведение.
|
|
|
| 7 | Формулы приведения.
|
|
|
Самостоятельная работа 6.2.
Задание: изготовить модель тригонометрического круга на плотной бумаге формата А4.
Показать линии тангенса и котангенса.
Форма выполнения задания: модель тригонометрического круга.
Самостоятельная работа 6.3.
Группа________________ Ф.И._______________________________________________________
Форма выполнения задания: решение уравнений.
Задание: решить тригонометрические уравнения.
Самостоятельная работа 7.1.
Форма выполнения задания: построение графика функции.
Задание: постройте график функции с помощью различных преобразований.
| Вариант 1 Построить график функции  | Вариант 2 Построить график функции  | Вариант 3 Построить график функции  | Вариант 4 Построить график функции  |
| Вариант 5 Построить график функции  | Вариант 6 Построить график функции  | Вариант 7 Построить график функции  | Вариант 8 Построить график функции  |
| Вариант 9 Построить график функции  | Вариант 10 Построить график функции  | Вариант 11 Построить график функции  | Вариант 12 Построить график функции  |
| Вариант 13 Построить график функции  | Вариант 14 Построить график функции  | Вариант 15 Построить график функции  | Вариант 16 Построить график функции  |
| Вариант 17 Построить график функции  | Вариант 18 Построить график функции  | Вариант 19 Построить график функции  | Вариант 20 Построить график функции  |
| Вариант 21 Построить график функции  | Вариант 22 Построить график функции  | Вариант 23 Построить график функции  | Вариант 24 Построить график функции  |
| Вариант 25 Построить график функции  | Вариант 26 Построить график функции  | Вариант 27 Построить график функции  | Вариант 28 Построить график функции  |
Самостоятельная работа7.2.
Форма выполнения задания: построение графика и описание свойств функции по графику.
Задание: с помощью преобразований графиков функций построить график заданной функции и указать её свойства.
| Вариант 1 С помощью преобразования графиков соответствующих функций постройте график функции  . Укажите: . Укажите: а) область определения; б) область значений; в) промежутки монотонности; | Вариант 2 С помощью преобразования графиков соответствующих функций постройте график функции  . Укажите: . Укажите: а) область определения; б) область значений; в) промежутки монотонности;
|
| Вариант 3 С помощью преобразования графиков соответствующих функций постройте график функции  . Укажите: . Укажите: а) область определения; б) область значений; в) промежутки монотонности; | Вариант 4 С помощью преобразования графиков соответствующих функций постройте график функции  . Укажите: . Укажите: а) область определения; б) область значений; в) промежутки монотонности |
| Вариант 5 С помощью преобразования графиков соответствующих функций постройте график функции  . Укажите: . Укажите: а) область определения; б) область значений; в) промежутки монотонности;
| Вариант 6 С помощью преобразования графиков соответствующих функций постройте график функции  . Укажите: . Укажите: а) область определения; б) область значений; в) промежутки монотонности; |
| Вариант 7 С помощью преобразования графиков соответствующих функций постройте график функции  . Укажите: . Укажите: а) область определения; б) область значений; в) промежутки монотонности; | Вариант 8 С помощью преобразования графиков соответствующих функций постройте график функции  . Укажите: . Укажите: а) область определения; б) область значений; в) промежутки монотонности;
|
| Вариант 9 С помощью преобразования графиков соответствующих функций постройте график функции  . Укажите: . Укажите: а) область определения; б) область значений; в) промежутки монотонности; | Вариант 10 С помощью преобразования графиков соответствующих функций постройте график функции  . Укажите: . Укажите: а) область определения; б) область значений; в) промежутки монотонности; |
| Вариант 11 С помощью преобразования графиков соответствующих функций постройте график функции  . Укажите: . Укажите: а) область определения; б) область значений; в) промежутки монотонности;
| Вариант 12 С помощью преобразования графиков соответствующих функций постройте график функции  . Укажите: . Укажите: а) область определения; б) область значений; в) промежутки монотонности;
|
| Вариант 13 С помощью преобразования графиков соответствующих функций постройте график функции  . Укажите: . Укажите: а) область определения; б) область значений; в) промежутки монотонности;
| Вариант 14 С помощью преобразования графиков соответствующих функций постройте график функции  . Укажите: . Укажите: а) область определения; б) область значений; в) промежутки монотонности;
|
| Вариант 15 С помощью преобразования графиков соответствующих функций постройте график функции  . Укажите: . Укажите: а) область определения; б) область значений; в) промежутки монотонности;
| Вариант 16 С помощью преобразования графиков соответствующих функций постройте график функции  . Укажите: . Укажите: а) область определения; б) область значений; в) промежутки монотонности;
|
| Вариант 17 С помощью преобразования графиков соответствующих функций постройте график функции  . Укажите: . Укажите: а) область определения; б) область значений; в) промежутки монотонности;
| Вариант 18 С помощью преобразования графиков соответствующих функций постройте график функции  . Укажите: . Укажите: а) область определения; б) область значений; в) промежутки монотонности; |
| Вариант 19 С помощью преобразования графиков соответствующих функций постройте график функции  . Укажите: . Укажите: а) область определения; б) область значений; в) промежутки монотонности;
| Вариант 20 С помощью преобразования графиков соответствующих функций постройте график функции  . Укажите: . Укажите: а) область определения; б) область значений; в) промежутки монотонности. |
| Вариант 21 С помощью преобразования графиков соответствующих функций постройте график функции  . Укажите: . Укажите: а) область определения; б) область значений; в) промежутки монотонности;
| Вариант 22 С помощью преобразования графиков соответствующих функций постройте график функции  . Укажите: . Укажите: а) область определения; б) область значений; в) промежутки монотонности;
|
|
Вариант 23 С помощью преобразования графиков соответствующих функций постройте график функции  . Укажите: . Укажите: а) область определения; б) область значений; в) промежутки монотонности;
|
Вариант 24 С помощью преобразования графиков соответствующих функций постройте график функции  . Укажите: . Укажите: а) область определения; б) область значений; в) промежутки монотонности;
|
| Вариант 25 С помощью преобразования графиков соответствующих функций постройте график функции  . Укажите: . Укажите: а) область определения; б) область значений; в) промежутки монотонности;
| Вариант 26 С помощью преобразования графиков соответствующих функций постройте график функции  . Укажите: . Укажите: а) область определения; б) область значений; в) промежутки монотонности; |
| Вариант 27 С помощью преобразования графиков соответствующих функций постройте график функции  . Укажите: . Укажите: а) область определения; б) область значений; в) промежутки монотонности | Вариант 28 С помощью преобразования графиков соответствующих функций постройте график функции  . Укажите: . Укажите: а) область определения; б) область значений; в) промежутки монотонности; |
Самостоятельная работа 8.1.Группа___________Ф.И.____________________________________
Задание: Решить задания на многогранники и тела вращения из единого банка ЕГЭ( вариантам)
Форма выполнения задания:Решение задач
1 вариант
Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 6 см и высота 4 см.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 см и 4 см, высота призмы равна 10 см. Найдите объем данной призмы.
Площадь осевого сечения цилиндра равна 4 м2. Найдите объем цилиндра.
Высота конуса равна  . образующая конуса составляет с плоскостью основания угол в
. образующая конуса составляет с плоскостью основания угол в  . Найти объем конуса.
. Найти объем конуса.
Площадь большого круга шара равна 3 см2. Найдите объем шара.
Самостоятельная работа 8.1. Группа___________Ф.И.____________________________________
Задание: Решить задания на многогранники и тела вращения из единого банка ЕГЭ( вариантам)
Форма выполнения задания:Решение задач
2 вариант
Найдите объём правильной треугольной пирамиды со стороной основания 6 см и высотой 1 см.
Найдите объем прямой призмы, в основании которой лежит ромб с диагоналями 6 см и 8 см и боковым ребром 10 см.
Осевое сечение цилиндра - квадрат. Площадь основания равна 1. Найдите объем цилиндра.
Радиус основания конуса равен 3 м, высота - 4 м. Найдите площадь объем конуса.
Сечение шара плоскостью, отстоящей от центра шара на расстоянии 8 см, имеет радиус 6 см. Найдите объем шара.
Самостоятельная работа 8.2.
Задание: изготовить модели многогранника и тела вращения.
Форма выполнения задания: модель многогранника и тела вращения.
Используя методические рекомендации, изготовьте модели изученныхтел.
Методические рекомендации
Многогранники
Одним из способов изготовления правильных многогранников является способ с использованием, так называемых, развёрток.
Если модель поверхности многогранника изготовлена из гибкого нерастяжимого материала (бумаги, тонкого картона и т. п.), то эту модель можно разрезать по нескольким рёбрам и развернуть так, что она превратится в модель некоторого многоугольника. Этот многоугольник называют развёрткой поверхности многогранника. Для получения модели многогранника удобно сначала изготовить развёртку его поверхности. При этом необходимыми инструментами являются клей и ножницы. Модели многогранников можно сделать, пользуясь одной разверткой, на которой будут расположены все грани. Однако в этом случае все грани будут одного цвета.
Тела вращения
Если модель поверхности тела вращения изготовлена из гибкого нерастяжимого материала (бумаги, тонкого картона и т. п.), то эту модель можно разрезать по образующей, отделить основание и развернуть так, чтобы она превратится в модель некоторого многоугольника плюс круг. Эту фигуру называют развёрткой поверхности тела вращения. Для получения модели тела вращения удобно сначала изготовить развёртку его поверхности. При этом необходимыми инструментами являются клей и ножницы. Модели тел вращения можно сделать, пользуясь одной разверткой, на которой будут расположены все элементы.
Используя развертки тел вращения, изготовьте их модели.
Самостоятельная работа 8.3.
Задание: решить тест и составить кроссворд «Многогранники»
Форма выполнения задания: кроссворд.
Вариант 1
Тетраэдр - это
поверхность, составленная из треугольников
поверхность, составленная из пяти треугольников
параллелограмм и четыре треугольника
поверхность, составленная из четырех треугольников
Многогранник - это
поверхность, составленная из n- параллелограммов
поверхность, составленная из n-многоугольников и n-треугольников
поверхность, составленная из многоугольников
поверхность, составленная из n-многоугольников и n-параллелограммов
Если боковые ребра призмы перпендикулярны к основаниям, то призма называется
правильной
прямой
наклонной
перпендикулярной
Площадь боковой поверхности прямой призмы равна
произведению периметра основания на высоту призмы
произведению периметра основания на апофему
произведению ребра основания на высоту призмы
произведению ребер основания на высоту призмы
Построить правильную усеченную четырехугольную пирамиду.
________________________________________________________________________
Вариант 2
Параллелепипед - это
поверхность, составленная из параллелограммов
поверхность, составленная из четырех параллелограммов
параллелограмм и четыре треугольника
поверхность, составленная из шести параллелограммов
Геометрическое тело - это
поверхность тела, ограничивающая его
связанная фигура в пространстве, которая содержит все свои граничные точки
ограниченная связанная фигура в пространстве, которая содержит все свои граничные точки
ограниченная фигура в пространстве, которая содержит все свои граничные точки
Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если
каждая фигура симметрична относительно некоторой фигуры
каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры
каждая точка фигуры симметрична относительно нее некоторой прямой той же фигуры
каждая точка фигуры симметрична относительно нее некоторой плоскости той же фигуры
Площадь полной поверхности пирамиды равна
сумме площадей всех ее граней
сумме квадратов трех его измерений
сумме площадей двух ее граней
произведению квадратов двух его измерений
Построить наклонную четырехугольную призму.
Вариант 3
Октаэдр - это
поверхность, составленная из девяти треугольников
поверхность, составленная из десяти треугольников
поверхность, составленная из шести треугольников
поверхность, составленная из восьми треугольников
Многогранник называется выпуклым, если
он расположен по разные стороны от каждой его вершины
он расположен по одну сторону от каждой его вершины
он расположен по одну сторону от плоскости каждой его грани
он расположен по разные стороны от плоскости каждой его грани
Выпуклый многогранник называется правильным, если
его боковые грани равные многоугольники
все его грани равные многоугольники
его боковые грани равные параллелограммы
не равны друг другу
все его грани равные параллелограммы
Площадь боковой поверхности правильной пирамиды равна
половине произведения периметра основания на апофему
произведению периметра основания на апофему
половине произведения периметра основания на высоту пирамиды
произведению периметра основания на высоту пирамиды
Построить наклонный параллелепипед.
________________________________________________________________________
Вариант 4
Призма - это
многогранник, составленный из двух многоугольников, расположенных в двух равных плоскостях и n - параллелограммов
многогранник, составленный из двух равных многоугольников, и n - параллелограммов
многогранник, составленный из двух равных многоугольников, расположенных в двух плоскостях и n - параллелограммов
многогранник, составленный из двух равных многоугольников, расположенных в параллельных плоскостях и n - параллелограммов
Фигура называется ограниченной, если
Какая фигура не имеет центра симметрии?
правильный октаэдр
правильный тетраэдр
правильный додекаэдр
правильный икосаэдр
Площадь боковой поверхности правильной усеченной пирамиды равна
произведению полусуммы периметров оснований на апофему
произведению суммы периметров оснований на апофему
произведению суммы периметров оснований на высоту пирамиды
произведению полусуммы периметров оснований на высоту пирамиды
Построить усеченную треугольную пирамиду.
Самостоятельная работа 9.1.
Форма выполнения задания: кроссворд.
Индивидуальное творческое задание: составить кроссворд «Производная».
Методические рекомендации по составлению кроссвордов
В процессе работы обучающиеся:
просматривают и изучают необходимый материал, как в лекциях, так и в дополнительных источниках информации;
составляют список слов раздельно по направлениям;
составляют вопросы к отобранным словам;
проверяют орфографию текста, соответствие нумерации;
оформляют готовый кроссворд.
Общие требования при составлении кроссвордов:
не допускается наличие "плашек" (незаполненных клеток) в сетке кроссворда;
не допускаются случайные буквосочетания и пересечения;
загаданные слова должны быть именами существительными в именительном падеже единственного числа;
двухбуквенные слова должны иметь два пересечения;
трехбуквенные слова должны иметь не менее двух пересечений;
не допускаются аббревиатуры (ЗиЛ и т.д.), сокращения (детдом и др.);
не рекомендуется большое количество двухбуквенных слов;
все тексты должны быть написаны разборчиво, желательно отпечатаны.
Требования к оформлению:
на каждом листе должна быть фамилия автора, а также название данного кроссворда;
рисунок кроссворда должен быть четким;
сетки всех кроссвордов должны быть выполнены в двух экземплярах:
1-й экз. - с заполненными словами;
2-й экз. - только с цифрами позиций.
Ответы публикуются отдельно. Ответы предназначены для проверки правильности решения кроссворда и дают возможность ознакомиться с правильными ответами на нерешенные позиции условий, что способствует решению одной из основных задач разгадывания кроссвордов — повышению эрудиции и увеличению словарного запаса.
Критерии оценивания составленных кроссвордов:
Четкость изложения материала, полнота исследования темы.
Оригинальность составления кроссворда.
Практическая значимость работы.
Уровень стилевого изложения материала, отсутствие стилистических ошибок.
Уровень оформления работы, наличие или отсутствие грамматических и пунктуационных ошибок.
Количество вопросов в кроссворде, правильное их изложения.
6. Методические рекомендации по оформлению рефератов
Титульный лист.
План работы оформляется с названием «Оглавление»; расположение – по центру.
Список библиографических источников оформляется под заголовком «Литература». Список литературы должен включать все использованные источники: сведения о книгах (монографиях, учебниках, пособиях, справочниках и т.д.) должны содержать: фамилию и инициалы автора, заглавие книги, место издания, издательство, год издания. При наличии трех и более авторов допускается указывать фамилию и инициалы только первого из них со словами «и др.». Наименование места издания надо приводить полностью в именительном падеже: допускается сокращение названия только двух городов: Москва (М.) и Санкт Петербург (СПб.). Приведенные библиографические источники должны быть отсортированы в алфавитном порядке по возрастанию. Список должен состоять не менее чем из трех источников.
Каждая новая часть работы, новая глава, новый параграф начинается с последующей страницы.
Приложение оформляются на отдельных листах, каждое приложение имеет порядковый номер и тематический заголовок. Надпись «Приложение» 1 (2.3...) оформляется в правом верхнем углу. Заголовок приложения оформляется как заголовок параграфа.
Объем работы не менее 10 листов напечатанных на компьютере (машинке) страниц; оглавление, список литературы и приложения не включаются в указанное количество страниц.
Текст рукописи печатается шрифтом № 14, с интервалом - 1,5.
Поля: слева - 3 см, справа - 1 см, сверху и снизу - 2 см.
Красная строка - 1,5 см .Межабзацный интервал – 1,8.
Название «Оглавление», «Введение», «Заключение», «Приложение», «Литература», а также заголовки глав и параграфов выделяются одинаковым темным, жирным шрифтом.
После цитаты в тексте работы используются знаки: «...», [1, С. 10], где номер библиографического источника берется из списка использованной литературы.
Обращение к тексту приложения оформляется следующим образом: (см. Приложение 1).
Оформление схем алгоритмов, таблиц и формул. Иллюстрации (графики, схемы, диаграммы) могут быть в основном тексте реферата и в разделе приложений. Все иллюстрации именуются рисунками. Все рисунки, таблицы и формулы нумеруются арабскими цифрами и имеют сквозную нумерацию в пределах приложения. Каждый рисунок должен иметь подпись. Например:
Рис.12. Форма главного окна приложения.
На все рисунки, таблицы и формулы в работе должны быть ссылки в виде: «форма главного окна приложения приведена на рис. 12.».
Рисунки и таблицы должны размещаться сразу после той страницы, на которой в тексте записки она упоминается в первый раз. Если позволяет место, рисунок (таблица) может размещаться в тексте на той же странице, где на него дается первая ссылка.
Если рисунок занимает более одной страницы, на всех страницах, кроме первой, проставляется номер рисунка и слово «Продолжение». Например:
Рис. 12. Продолжение
Рисунки следует размещать так, чтобы их можно было рассматривать без поворота записки. Если такое размещение невозможно, рисунки следует располагать так, чтобы для их просмотра надо было бы повернуть работу по часовой стрелке.
Схемы алгоритмов должны быть выполнены в соответствии со стандартом ЕСПД. Толщина сплошной линии при вычерчивании схем алгоритмов должна быть в пределах от 0,6 до 1,5 мм. Надписи на схемах должны быть выполнены чертежным шрифтом. Высота букв и цифр должна быть не менее 3,5 мм.
Номер таблицы размещается в правом верхнем углу над заголовком таблицы, если он есть. Заголовок, кроме первой буквы, выполняется строчными буквами. В аббревиатурах используются только заглавные буквы. Например: ПЭВМ.
Ссылки на таблицы в тексте пояснительной записки должны быть в виде слова табл. и номера таблицы. Например: Результаты тестов приведены в табл. 4.
Номер формулы ставится с правой стороны страницы в круглых скобках на уровне формулы. Например: z:=sin(x)+cos(y); (12).
Ссылка на номер формулы дается в скобках.
Например: расчет значений производится по формуле (12).
Нумеровать страницы работы по книжному варианту: печатными цифрами, в нижнем правом углу страницы, начиная с текста «Введения» (с. 3). Работа нумеруется сквозно, до последней страницы.
В оглавлении указываются начальные страницы всех частей и параграфов работы (название главы отдельной страницы не имеет), кроме списка литературы и приложений (в тексте нумеруются).
Пишется слово «глава», главы нумеруются римскими цифрами, параграфы - арабскими, знак ; не пишется; части работы «Введение». «Заключение», «Литература» нумерации не имеют.
Названия глав и параграфов пишутся с красной строки.
Заголовки «Введение», «Заключение», «Литература» пишутся посередине, вверху листа, без кавычек, точка не ставится.
Объем введения и заключения работы - 1,5-2 страницы печатного текста.
Работа должна быть прошита.
Самостоятельная работа 9.4.
Форма выполнения задания: Построить график функции.
Индивидуальное задание: «Исследование функций с помощью производной»
Цель работы: научить студентов применять производную при исследовании функций.
Теоретический материал
Общая схема исследования функций с помощью производной.
Нахождение области определения функции.
Проверка того, является ли функция четной, нечетной, периодической или эта функция – функция общего вида.
Определение точек пересечения с осями координат.
Нахождение критических точек
( точек, в которых производная равна нулю или не существует).
Определение промежутков знакопостоянства функции.
Определение промежутков возрастания и убывания функции
(промежутков, на которых производная положительна или отрицательна).
Определение экстремумов функции.
Исследование функции на выпуклость, вогнутость, определение точек перегиба (исследование проводится по второй производной функции).
Нахождение асимптот функции.
Уточнение графика функции по точкам (произвести окончательное уточнение графика, в особенности на участках, где информация о нем недостаточна).
Данную схему можно варьировать в зависимости от конкретных особенностей функции, переставлять отдельные этапы, некоторые из них опускать, какие-то, наоборот, добавлять.
Индивидуальные задания для студентов
Исследуйте функцию с помощью производной и постройте ее график: f(x) = 3x – x3 | Исследуйте функцию с помощью производной и постройте ее график: f(x) = x3 – 12x |
Исследуйте функцию с помощью производной и постройте ее график: f(x) = x3 – 12x x3 – 12x | Исследуйте функцию с помощью производной и постройте ее график: f(x) = 5x -  x3 x3 |
| 5. Исследуйте функцию с помощью производной и постройте ее график: f(x) = x3 – 3x – 1 x3 – 3x – 1 | 6. Исследуйте функцию с помощью производной и постройте ее график: f(x) = 2 +  x3 x3 |
| 7. Исследуйте функцию с помощью производной и постройте ее график: f(x) = 1 + 4x -  x3 x3 | 8. Исследуйте функцию с помощью производной и постройте ее график: f(x) = x3 – x + 3 x3 – x + 3 |
| 9. Исследуйте функцию с помощью производной и постройте ее график:f(x) = 4x3 – 6x2 | 10. Исследуйте функцию с помощью производной и постройте ее график:f(x) = 3x2 – x3 |
| 11. Исследуйте функцию с помощью производной и постройте ее график:f(x) =3x2 – 2x3 | 12. Исследуйте функцию с помощью производной и постройте ее график:f(x) = x3 + 3x2 |
| 13. Исследуйте функцию с помощью производной и постройте ее график:f(x) = 4x3 - 6x2 | 14. Исследуйте функцию с помощью производной и постройте ее график:f(x) = -x3 -3x2 |
| 15. Исследуйте функцию с помощью производной и постройте ее график: f(x) = 2x3 + 3x2 - 2 | 16. Исследуйте функцию с помощью производной и постройте ее график: f(x) = 1 + 3x2 – 2x3 |
| 17. Исследуйте функцию с помощью производной и постройте ее график: f(x) = 1 – 3x2 – x3 | 18. Исследуйте функцию с помощью производной и постройте ее график: f(x) = x3 - 3x2 + 3 |
| 19. Исследуйте функцию с помощью производной и постройте ее график: f(x) = x3 – 2x2 + 1 x3 – 2x2 + 1 | 20. Исследуйте функцию с помощью производной и постройте ее график: f(x) = 2 + x2 -  x3 x3 |
| 21. Исследуйте функцию с помощью производной и постройте ее график: f(x) = 4 + 3x – x2 -  x3 x3 | 22. Исследуйте функцию с помощью производной и постройте ее график: f(x) =  x3 + x3 +  x2 -2x - x2 -2x -  |
| 23. Исследуйте функцию с помощью производной и постройте ее график: f(x) = x3 – 6x2 + 9x - 3 | 24. Исследуйте функцию с помощью производной и постройте ее график: f(x) = x3 + 6x2 + 9x + 8 |
| 25. Исследуйте функцию с помощью производной и постройте ее график: f(x) = 8x2 - x4 - 7 | 26. Исследуйте функцию с помощью производной и постройте ее график: f(x) = x4 - -2x2 – 5 |
| 27. Исследуйте функцию с помощью производной и постройте ее график: f(x) = x4 -2x2 – 6 | 28. Исследуйте функцию с помощью производной и постройте ее график: f(x) = -x4 + 2x2 + 3 |
| 29. Исследуйте функцию с помощью производной и постройте ее график: f(x) = x3 – 3x | 30. Исследуйте функцию с помощью производной и постройте ее график: f(x) = x3 + 3x2 |
Самостоятельная работа 9.3.
Группа______
Ф.И.______________________________
Решить кроссворд
Кроссворд
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 
|
|
| 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 4 |
|
|
|
|
|
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
| 2 |
|
|
|
| 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По вертикали: 1.Создатель дифференциального исчисления, использовавший понятие бесконечно малой.
2. Коэффициент пропорциональности между бесконечно малыми изменениями взаимосвязанных величин.
3. Создатель дифференциального исчисления, опирающийся на физическое представление о мгновенной скорости, считавший его очевидным и сводящий к нему другие случаи производной.
4. Производная от работы по времени.
5.Производная от количества электричества по времени - …?…. тока.
По горизонтали:
Производная от скорости по времени.
Производная от пути по времени.
Производная от массы неоднородного стержня по длине – линейная …….?……. .
Самостоятельная работа 9.3. Группа_____ Ф.И.______________________________________
Форма выполнения задания: таблица с ответами.
Практическое задание: выполнить тест по теме «Производная».
| Вариант 1 1.Производная функции  равна: равна: а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  . . 2.Производная функции  в точке в точке  равна: равна:
а) –1,5; б) 1,5; в) –0,75; г) 0,75. 3.Какая из приведенных функций является производной функции  ? ? а)  ; б) ; б)  ; в) ; в)  ; ; г)  . . 4. Точка движется прямолинейно по закону . Какой формулой задается скорость движения этой точки в момент времени t. . Какой формулой задается скорость движения этой точки в момент времени t. 5. Угловой коэффициент касательной, проведенной к графику функции  в точке с положительной абсциссой в точке с положительной абсциссой  , равен 2. Найдите , равен 2. Найдите  . . | Вариант 2 1.Производная функции  равна: равна: а)  ; б) ; б)  ; в) ; в)  ; г) ; г)  . . 2. Производная функции  в точке в точке  равна: равна: а) 1,2; б) 2; в) –1,2; г) 2,5. 3. Какая из приведенных функций является производной функции  ? ? а)  ; б) ; б)  ; в) ; в)  ; ; г)  . . 4. Тело движется по прямой так, что его скорость v (м/с) изменяется по закону  . Какую скорость приобретает тело в момент, когда его ускорение равно 12м/с2. . Какую скорость приобретает тело в момент, когда его ускорение равно 12м/с2. 5.Найдите угловой коэффициент касательной, проведенной к параболе  в точке с абсциссой в точке с абсциссой
 . .
|
Ответы к задачам:
Форма выполнения задания: таблица с ответами.
Самостоятельная работа 10.1.
Форма выполнения задания: тест.
Задание: составить тест «Первообразная»
Тест должен содержать не менее 6-7 заданий и по 3-4 ответа к каждому заданию (верный только один).Включить задания двух видов:
Вычисление первообразных различных функций.
Вычисление первообразной, график которой проходит через точку с заданными координатами.
Самостоятельная работа 10.2.
Задание: выполнить графическую работу «Вычисление площадей фигур с помощью интеграла»
| Вариант 1 По готовому чертежу найтиплощадьзаштрихованной фигуры. 2. Вычислите площадь фигуры, ограниченной линиями  . . | Вариант 2 1.По готовому чертежу найтиплощадь заштрихованной фигуры. 2. Вычислите площадь фигуры, ограниченной линиями  . . |
| Вариант 3 1.По готовому чертежу найтиплощадь заштрихованной фигуры. 2. Вычислите площадь фигуры, ограниченной линиями  | Вариант 4 1.По готовому чертежу найтиплощадь заштрихованной фигуры. 2. Вычислите площадь фигуры, ограниченной линиями |
| Вариант 5 1. По готовому чертежу найтиплощадь заштрихованной фигуры. 2. Вычислите площадь фигуры, ограниченной линиями | Вариант 6 1. По готовому чертежу найтиплощадь заштрихованной фигуры. 2. Вычислите площадь фигуры, ограниченной линиями  |








 - читаем: корень 3-ей степени из 2-х;
- читаем: корень 3-ей степени из 2-х; - читаем: корень 5-ой степени из с
- читаем: корень 5-ой степени из с ,
, 
 = bbn = a
= bbn = a = 2 23 = 8
= 2 23 = 8 = 3 34 = 81
= 3 34 = 81 =
=  = 5 52 = 25
= 5 52 = 25 = -3 (-3)3 = -27
= -3 (-3)3 = -27 =
=  (
( 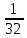
 =
= =
= =
= =
= ∙
∙ =
= 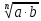
 ∙
∙  =
=  =
=









