Внеклассное мероприятие по математики "Увлекательное путешествие на корабле «Математика» к острову…"

Увлекательное путешествие на корабле «Математика» к острову…

МБОУ «Полесская СОШ»

учитель математики: Жигач Т.П.

Какой цифрой заканчивается число 1∙ 2 ∙3 ∙4 ∙5 ∙… ∙11 ∙12?

А)2

В)8

С)0

Д)1

Е)5

1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙… ∙ 1 0 ∙ 11 ∙ 12 = ……..0

В течение суток ¼ времени кошка ест, а остальное она спит. Сколько часов в сутки кошка спит?

А)16

В)18

С)6

Д)12

Е)20

24 : 4 ∙1 = 6(ч) – кошка ест

24 – 6 = 18(ч) – кошка спит

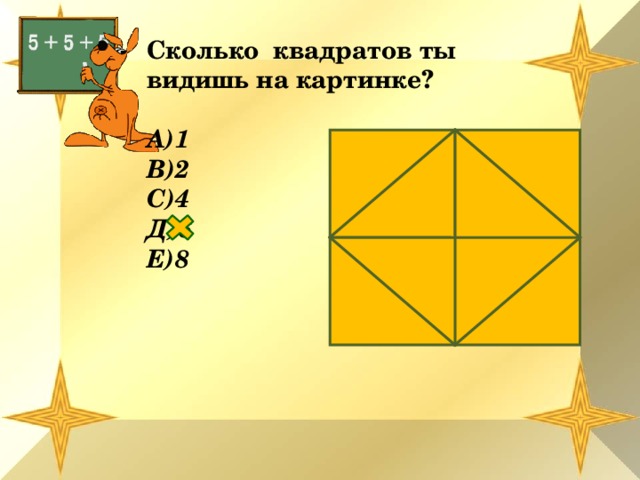
Сколько квадратов ты видишь на картинке?

А)1

В)2

С)4

Д)6

Е)8

Старый будильник отстаёт на 8 минут за каждые 24 часа. На сколько минут надо поставить его вперёд в 20.00, чтобы он зазвонил вовремя в 8 часов утра следующего дня?

А)1 мин 40 сек.

В)4 мин

С)1 мин

Д)2 мин 40 сек

Е)6 мин

Если за 24 часа будильник отстаёт на 8 минут, то за 12 часов он отстанет на 4 минуты.

Клетки пирамиды были заполнены по следующему правилу: над каждыми двумя числами записали их среднее арифметическое. Некоторые числа стёрли. Какое число было в верхней клетке? А)5

В)7

С)8

Д)14

Е)16

7

8

6

7

9

5

Представители 12 стран составили 30 задач для проведение конкурса – игры «Кенгуру». Каждая задача обсуждалась 10 минут. Сколько времени шло заседание?

А) 360 минут

В) 300 минут

С) 120 минут

Д) 52 минут

Е) 40 минут

30 ∙ 10 = 300 (минут)

У каждого марсианина по 3 руки. Десять марсиан построились в шеренгу, и каждый взял соседа за руку. Сколько рук остались свободными?

А)9

В)10

С)11

Д)12

Е)0

У первого и последнего марсианина останутся две свободные руки, а восьми марсиан – по одной. Значит, всего свободными останутся 12 рук.

Полученные результаты ответов расставь в порядке возрастания и соотнеси с данными буквами

0 – д

18 –л

6 –р

300 –е

4 –и

7 – и

12 - х

ДИРИХЛЕ

Петер Густав Лежен Дирихле (13.2.1805 - 5.5.1859) - немецкий математик, иностранный член-корреспондент Петербургской Академии наук (1837), член многих других академий .

Тема:

ПРИНЦИП ДИРИХЛЕ

в задачах

Цель занятия:

• Научиться решать задачи с помощью утверждений

-принципа Дирихле

n , то хотя бы в одной клетке сидят, по крайней мере, два кролика " width="640"

КРОЛИКИ и КЛЕТКИ

Если в n клетках

сидит m кроликов,

причем m n ,

то хотя бы в одной клетке сидят,

по крайней мере, два кролика

КЛЕТКИ и ГОЛУБИ

Если в n клетках

сидят m голубей,

причем m n ,

то хотя бы одна клетка останется свободной

n) , то найдётся клетка, в которой не менее m / n кроликов» Доказательство (от противного): Допустим, что в каждой клетке число кроликов не более, чем m / n . Тогда в n клетках кроликов не более, чем n · m / n = m . Противоречие! " width="640"

общая формулировка принципа Дирихле :

• «Если m кроликов сидят в n клетках (mn) , то найдётся клетка, в которой не менее m / n кроликов»

• Доказательство (от противного):

Допустим, что в каждой клетке число кроликов не более, чем m / n . Тогда в n клетках кроликов не более, чем n · m / n = m .

Противоречие!

Алгоритм применения принципа Дирихле

Определить что в задаче является "клетками", а что — "кроликами"

Применить соответствующее утверждение принципа Дирихле

?

В классе 15 учеников. Докажите, что найдутся, как минимум, 2 ученика, отмечающих дни рождения в один месяц.

Внутри равностороннего треугольника со стороной 1см расположено 5 точек. Докажите, что расстояние между некоторыми двумя из них меньше 0,5см

В 7 «Г» классе учится 27 школьников, знающих 109 песен. Докажите, что найдется школьник, знающий не менее 5 песен.

Работа в группах