Внеклассное мероприятие по математике
«Представление проекта: Возможна ли жизнь без зависимостей?»
Выполнила: Жижерина Наталья Викторовна, учитель информатики и математики МБОУ «СОШ №3 г. Щигры Курской области» и группа учащихся 11 класса.
«...Именно функция является тем средством математического языка, которое позволяет описывать процессы движения, изменения, присущие природе».
Г.Галилей
Цели:
Популяризация понятия функции;
расширение математического кругозора;
развитие познавательного интереса и творческой активности.
Оборудование: таблицы, графики функций, компьютер, видеопроектор, презентация.
План проведения
I. Постановка целей и задач.
II. Многообразие функциональных зависимостей.
III. Сообщения учащихся.
Почему не бывает животных какой угодно величины?
Почему летом жарко?
Звездное небо и логарифмы.
Где встречается парабола?
IV. История развития понятия функции.
V. Значимость изучения функциональных зависимостей.
I. Постановка целей и задач.
Наш проект посвящен функциям. Значение их велико. Функции и реальный мир неотделимы. Они описывают явления в природе. Устанавливают закономерности, помогают открывать законы, которые служат человечеству.
II. Многообразие функциональных зависимостей.
Ведущий, читает слова Галилея: «Именно функция является тем средством математического языка, которое позволяет описывать процессы движения, изменения присущие природе».
«Функция выражает зависимость между переменными величинами. Каждая область знаний: химия, физика, биология, социология и др. имеет свои объекты изучения, устанавливает свойства и взаимосвязи между этими объектами в реальном мире».
Сейчас многие науки берут на вооружение математический аппарат. Такие функциональные зависимости, например, возраст деревьев, развитие амебы, развитие папоротника изучает наука биология.
Функции помогают описывать процессы механического движения тел, небесных и земных. С помощью них ученые рассчитывают траектории движения космических кораблей и решают множество технических проблем.
III. Сообщения учащихся.
Выступления учащихся.
1. Почему не бывает животных, какой угодно величины?
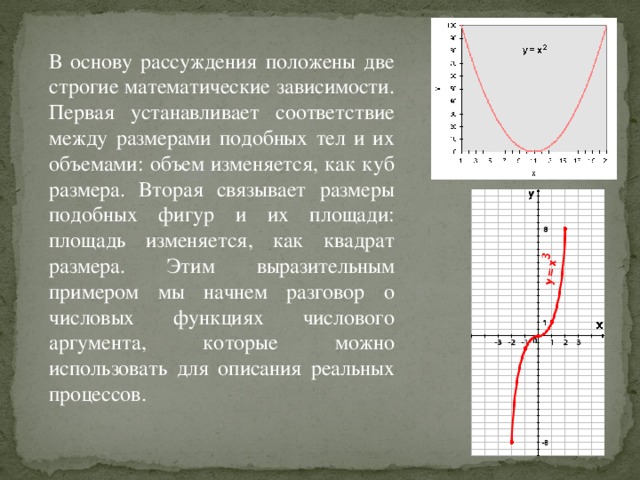
Почему, например, нет слонов в три раза большего роста, чем существуют, но тех же пропорций? Ответ таков: стань слон в три раза больше, вес его тогда увеличился бы в двадцать семь раз, как куб размера, а площадь сечения костей и, следовательно, их прочность — только в девять раз, как квадрат размера. Прочности костей уже не хватило бы, чтобы выдержать непомерно увеличившийся вес. Такой слон был бы раздавлен собственной тяжестью..
В основу рассуждения положены две строгие математические зависимости. Первая устанавливает соответствие между размерами подобных тел и их объемами: объем изменяется, как куб размера. Вторая связывает размеры подобных фигур и их площади: площадь изменяется, как квадрат размера. Этим выразительным примером мы начнем разговор о числовых функциях числового аргумента, которые можно использовать для описания реальных процессов.
Ведущий: «О солнце! Без тебя не стало б в мире жизни». «Да будет свет!»
2. Почему летом жарко?
Многие считают, что летом жарче т.к. Земля находится ближе всего к Солнцу, но это не так.
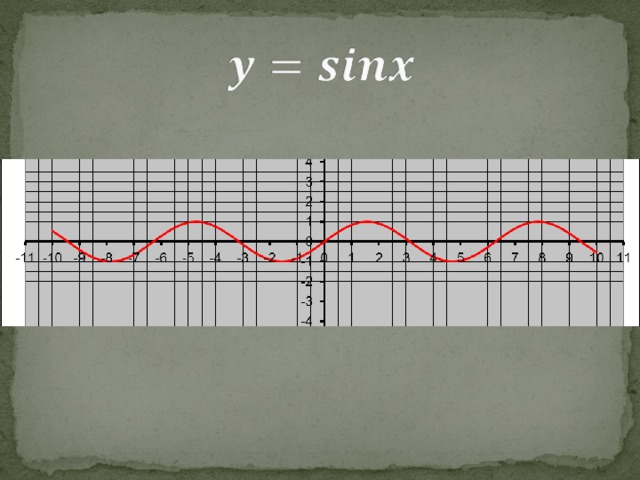
Орбита Земли - это почти круг, в центре которого находится Солнце. И расстояние от Земли меняется незначительно из месяца в месяц. Все дело в наклоне земной оси по отношению к плоскости земной орбиты. Зимой у нас Солнце невысоко поднимается над горизонтом, его лучи лишь скользят по земле. Летом Солнце приближается к Зениту, лучи его падают почти отвесно. Поток солнечной энергии одинаков во все времена. Он зависит от угла падения лучей. Меняется угол падения, меняется и доля Солнечной энергии. Зависимость солнечной энергии от угла падения лучей и выражает график у = sin x.
Ведущая читает слова М.В. Ломоносова:
«Открылась бездна, звезд полна;
Звездам числа нет, бездне дна.»
3.Звёздное небо и логарифмы.
Древнегреческий астроном Гиппарх насчитал на небе около тысячи звезд и разбил их по видимому блеску на шесть групп, самые яркие Гиппарх назвал звездами первой величины, менее яркие – второй и так далее в порядке равномерного убывания видимого блеска – до звезд, едва видимых невооруженным глазом, которым была присвоена шестая величина. С изобретением чувствительных приборов стало возможным точно определить блеск звезд. Стало возможным сравнить, насколько соответствует данным таких измерений традиционное распределение звезд по видимому блеску, произведенное на глаз.
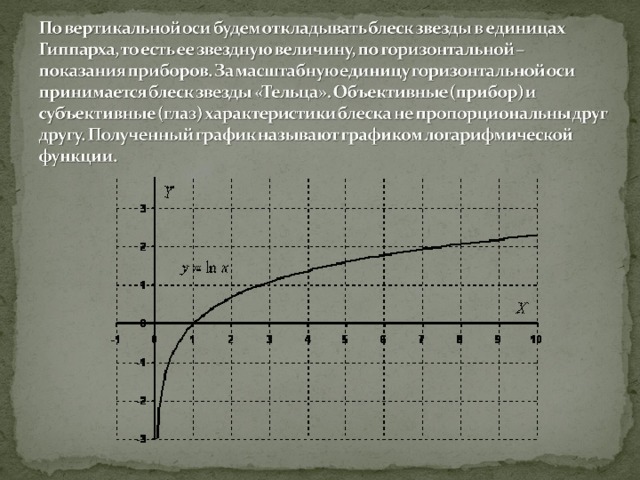
По вертикальной оси будем откладывать блеск звезды в единицах Гиппарха, то есть ее звездную величину, по горизонтальной – показания приборов. За масштабную единицу горизонтальной оси принимается блеск звезды «Тельца». Объективные (прибор) и субъективные (глаз) характеристики блеска не пропорциональны друг другу. Полученный график называют графиком логарифмической функции.
Именно эта функция позволяет по массе израсходованного топлива указать скорость ракеты (формула К.Э. Циолковского).
4. Где встречается парабола?
Пусть мяч подбросили вертикально вверх с высоты 1,5 м, придав ему начальную скорость 10м/с². Тогда высота h (в м), на которой находится мяч, есть квадратичная функция времени полета t (в с). Если считать, что g =10 м/с, то функцию h= f(t) можно описать формулой h= 1,5+10t-5t². График этой функции - часть параболы.
Показ фильма.
IV. История возникновения понятия функции.
Ведущий: "…ни одно из других понятий не отражает явлений реальной действительности с такой непосредственностью и с такой конкретностью, как понятие функциональной зависимости, в которой воплощены и подвижность, и динамичность реального мира, и взаимная обусловленность реальных величин". ( А.Я. Хинчин)
Идея функциональной зависимости восходит к древности. Ее содержание обнаруживается уже в первых математически выраженных соотношениях между величинами, в первых правилах действий над числами, в первых формулах для нахождения площади и объема тех или иных фигур.
Примерами табличного задания функции могут служить астрономические таблицы вавилонян, древних греков и индийцев, а примерами словесного задания функции - теорема о постоянстве отношения площадей круга и квадрата на его диаметре
Так, вавилонские ученые (4-5тыс.лет назад) установили, что площадь круга является функцией от его радиуса посредством нахождения грубо приближенной формулы: S=3r².
Графическое изображение зависимостей широко использовали Галилео Галилей, Пьер Ферма, Рене Декарт, который ввел «понятие переменной величины».
Путь к появлению понятия функции заложили в 17 веке французские ученые Франсуа Виет и Рене Декарт; они разработали единую буквенную математическую символику, которая вскоре получила всеобщее признание. Введено было единое обозначение: неизвестных - последними буквами латинского алфавита x, y, z, ... - известных - начальными буквами того же алфавита - a, b, c, ... и т.д. Тем самым появилась возможность записывать общие формулы.
Само слово “функция” (от латинского functio - совершение, выполнение) впервые было употреблено Лейбницем в 1673г. в письме к Гюйгенсу (под функцией он понимал отрезок, длина которого меняется по какому-нибудь определенному закону). В печати он ввел этот термин с 1694 года. Начиная с 1698 года, Лейбниц ввел также термины “переменная” и “константа”.
Следующий шаг в развитии понятия функции сделал гениальный ученик Бернулли, член Петербургской Академии наук Леонард Эйлер (1707 – 1783). Он писал: «Когда некоторые количества зависят друг от друга таким образом, что при изменении последних и сами они подвергаются изменению, то первые называют функцией вторых».
V. Значимость изучения функциональных зависимостей.
Учитель:
Знание законов природы дало человеку возможность объяснять и предсказывать ее разнообразнейшие явления. «Математическими портретами» закономерностей природы и служит функция.
Сегодня мы проследили за функциональными зависимостями в окружающем мире. Оценили их роль в практической деятельности человека, убедились в необходимости изучения функции.
Кто–то из вас серьезнее будет относиться к изучению математики, а некоторые займутся исследовательской деятельностью. Удачи всем.