«Необходимое и достаточное условие возрастания и убывания функции. Экстремумы функции»
Возрастание и убывание функции 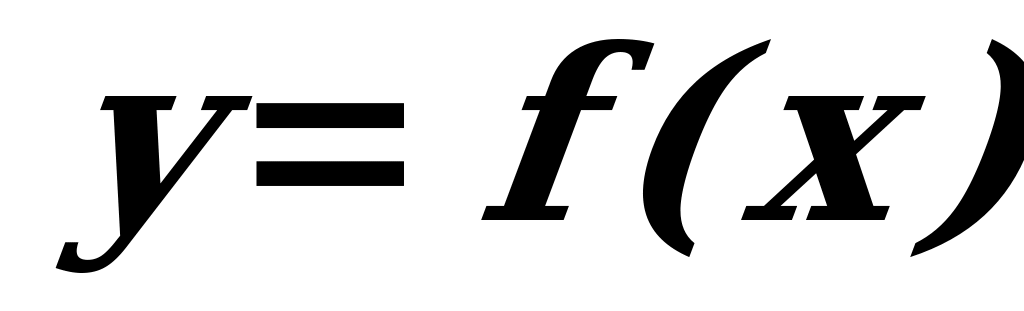 характеризуется знаком ее производной: если на некотором промежутке
характеризуется знаком ее производной: если на некотором промежутке 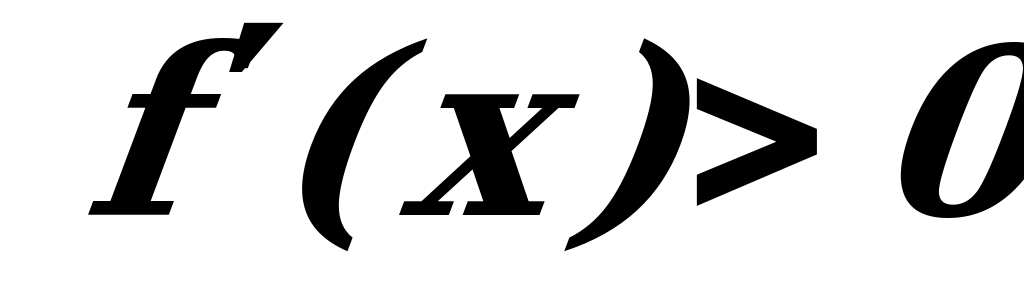 , то функция на этом промежутке возрастает; если же
, то функция на этом промежутке возрастает; если же 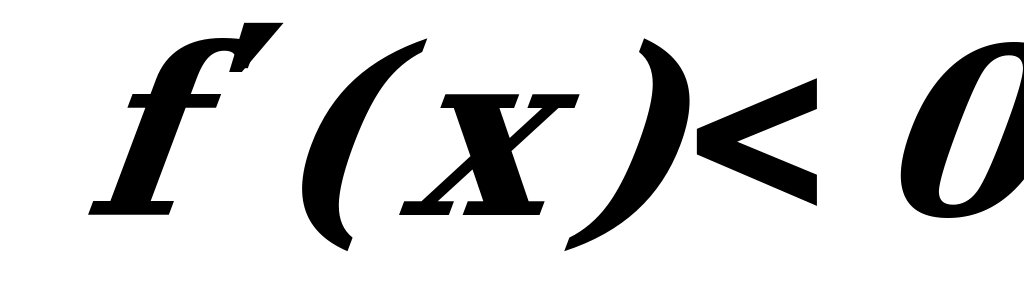 , то функция на этом промежутке убывает.
, то функция на этом промежутке убывает.
ПЛАН для нахождения промежутков возрастания и убывания функции y = f(x)
1. Находим f’(x)
2. f’(x) = 0 (находим нули функции производной 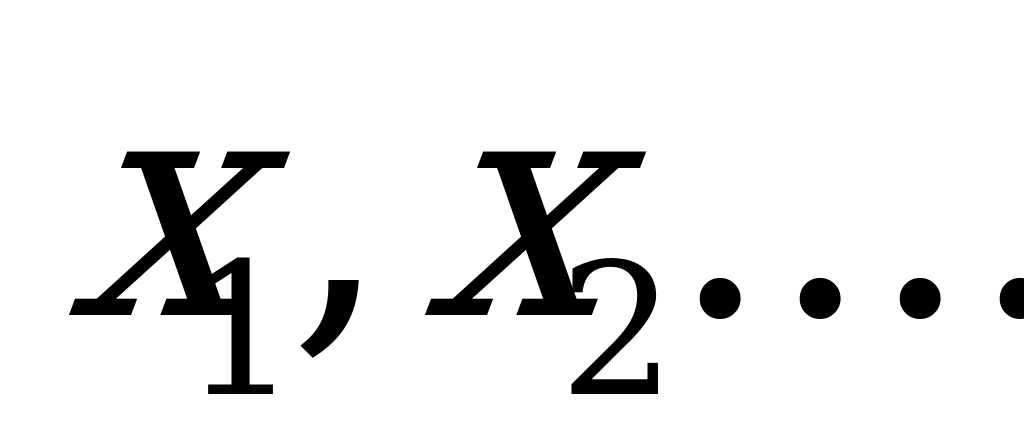 )
)
3. Отмечаем нули функции на числовой прямой, изображаем интервалы (вспоминаем метод интервалов)
4. Определяем знаки ПРОИЗВОДНОЙ на получившихся интервалах ( + или -)
Определяем монотонность функции:
-
Если на промежутке мы получили знак + тогда функция y = f(x)возрастает (рисуем под эти интервалом стрелочку вверх)
-
Если на промежутке мы получили знак - тогда функция y = f(x)убывает (рисуем под эти интервалом стрелочку вниз)
5. Записываем ответ (т.к. мы ищем промежутки возрастания или убывания функции, то в ответ мы запишем промежутки возрастания и промежутки убывания функции, а именно: y=f(x) возрастает, если х ∈…..).
Пример. Найти промежутки возрастания и убывания функции (заметьте, функцию можно обозначать различными способами):
а) 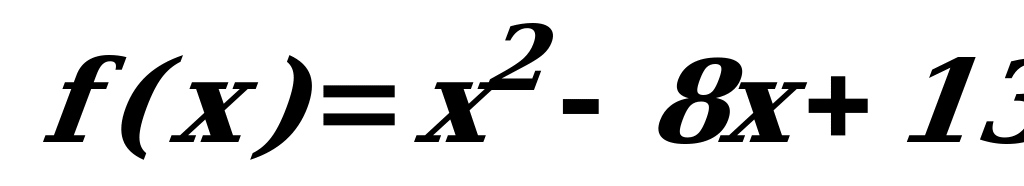
б) 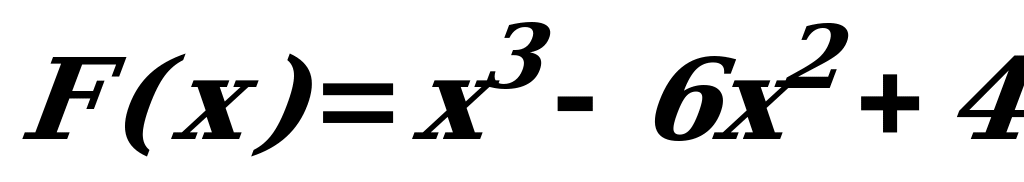
в) 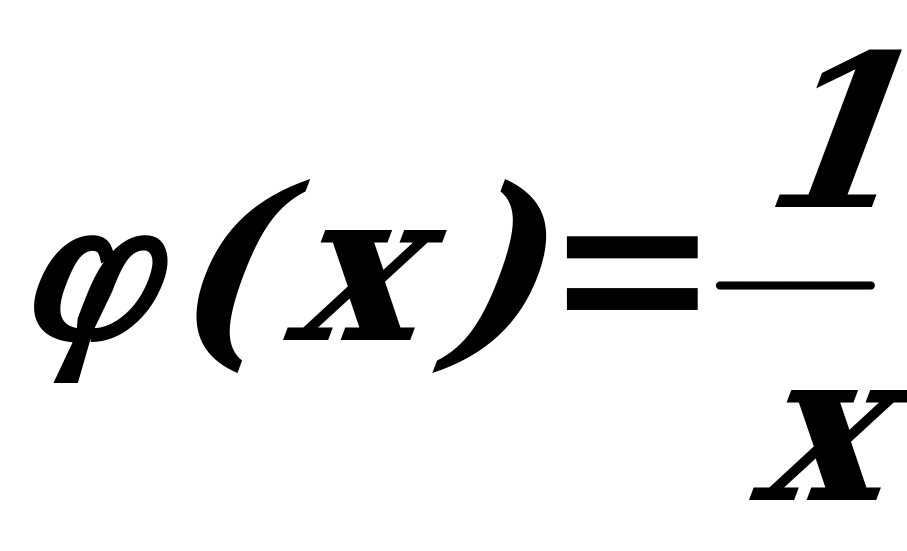
г) 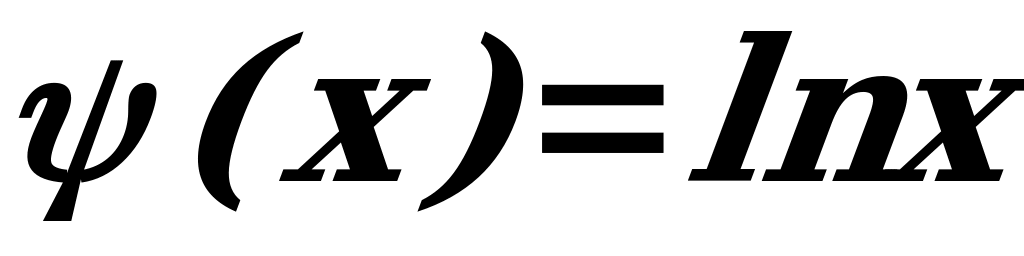
Решение.
а) см. план
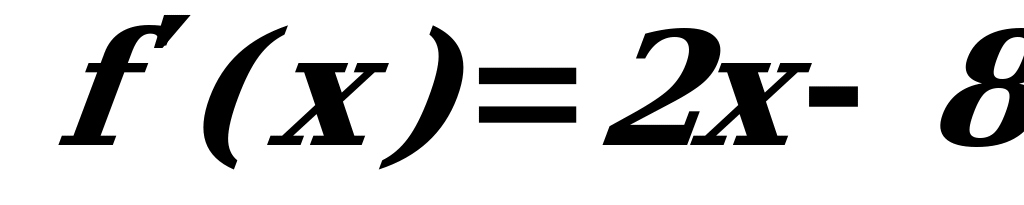
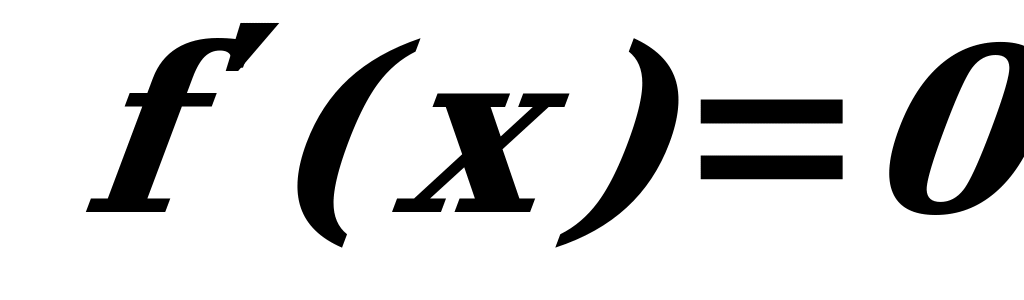
2х-8=0 =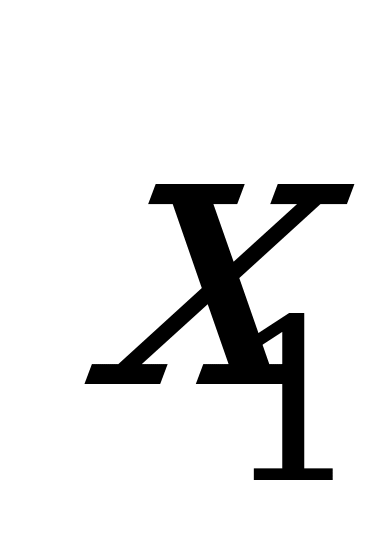 =4
=4
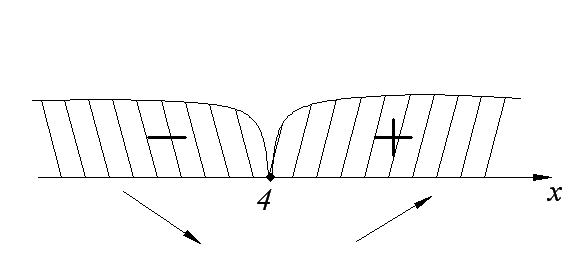
Вычислив значения 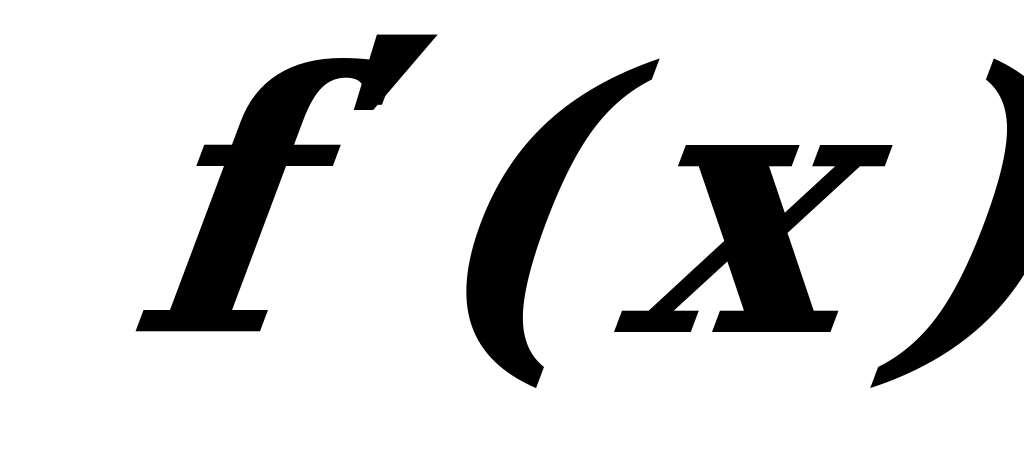 для любого значения
для любого значения 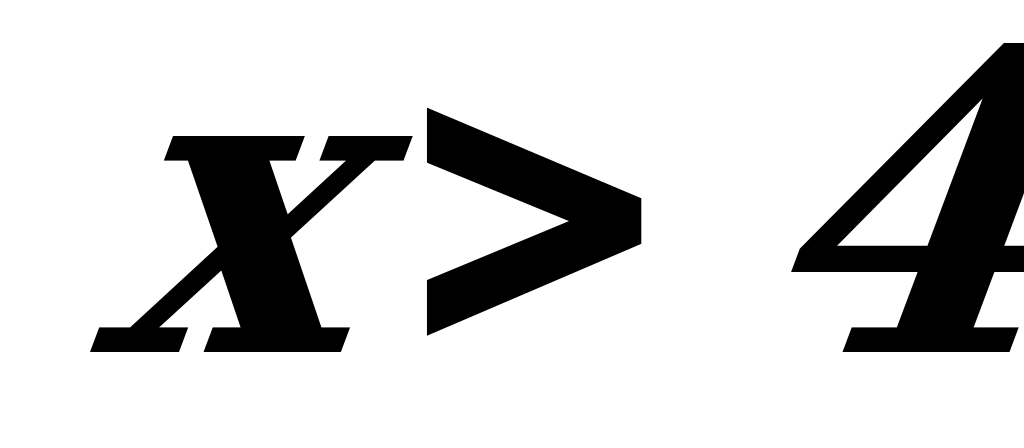 (например,
(например, 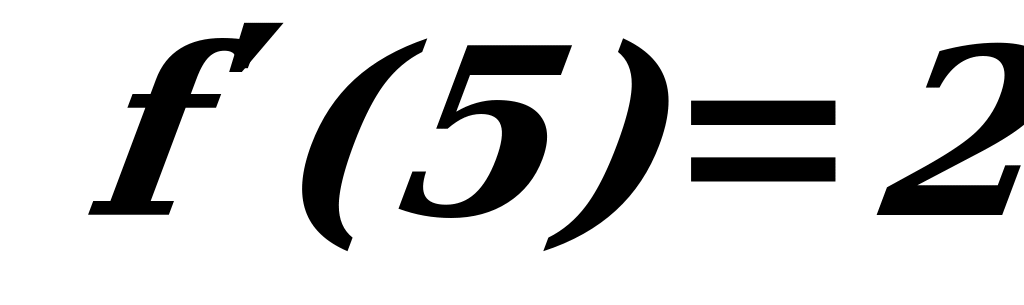 - подставили в f’значение х=5), заключаем, что на этом интервале производная
- подставили в f’значение х=5), заключаем, что на этом интервале производная 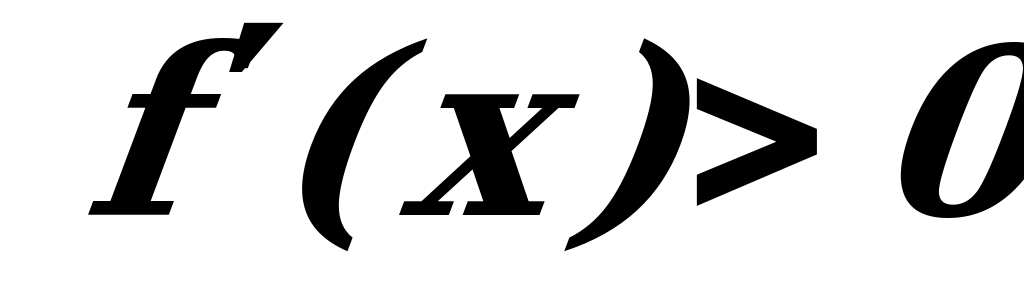 , следовательно, функция
, следовательно, функция 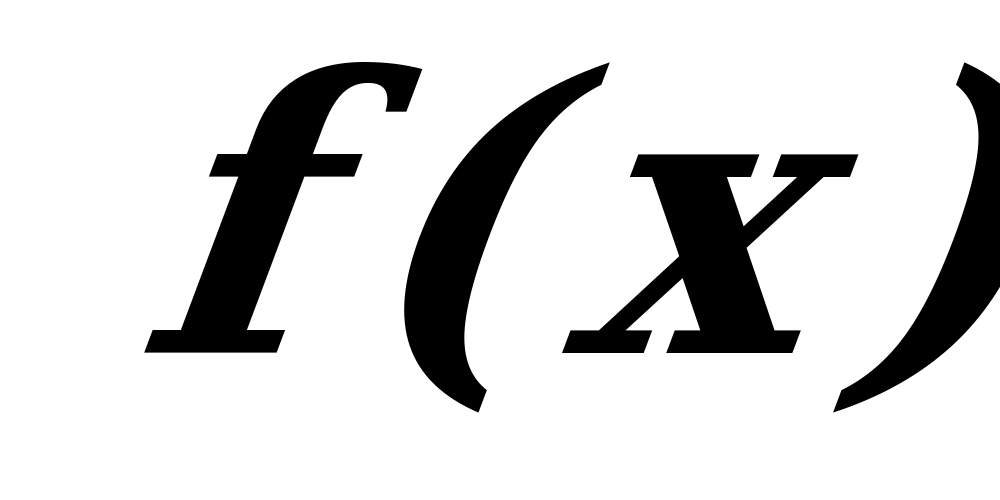 производная
производная 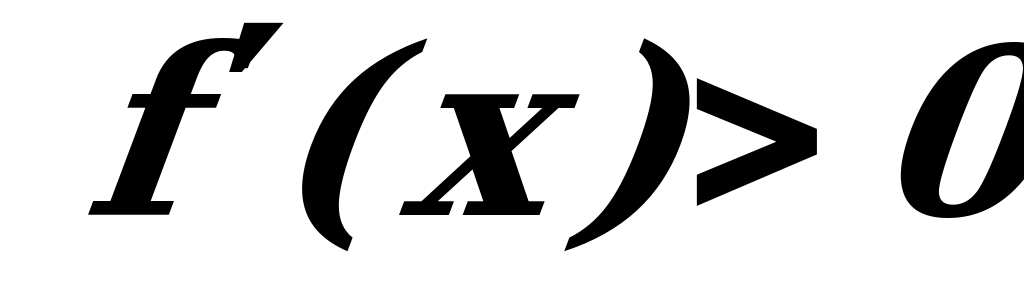 , следовательно, на этом интервале функция
, следовательно, на этом интервале функция 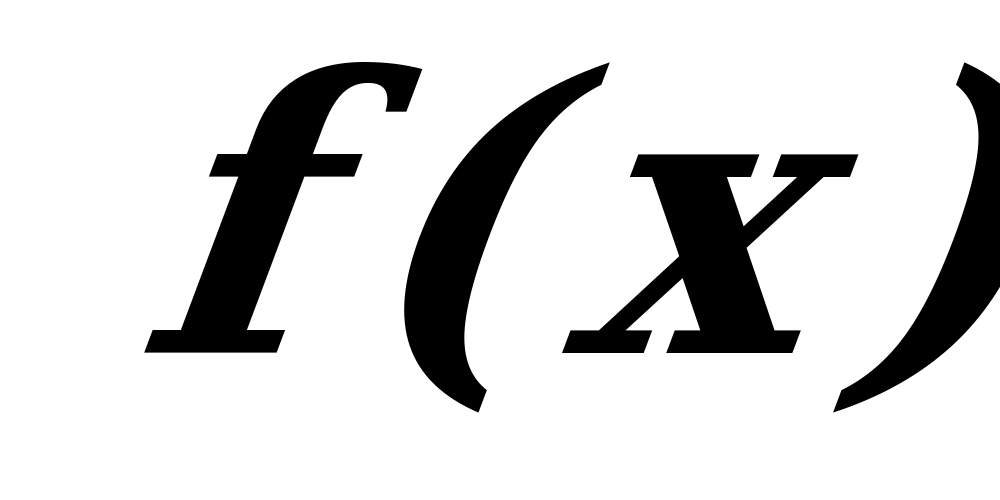 убывает.
убывает.
Ответ: y = f(x) возрастает, если х∈(4; +∞); y = f(x) убывает, если х∈(-∞;4).
-
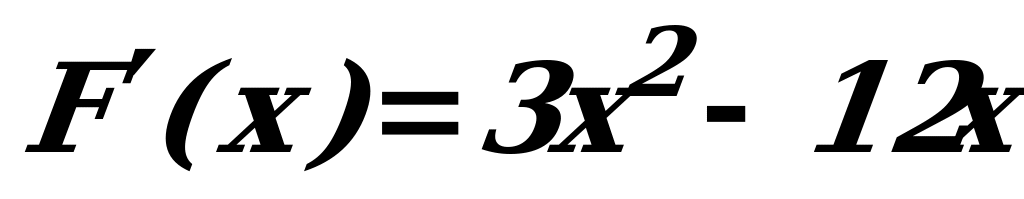 ; корни производной
; корни производной 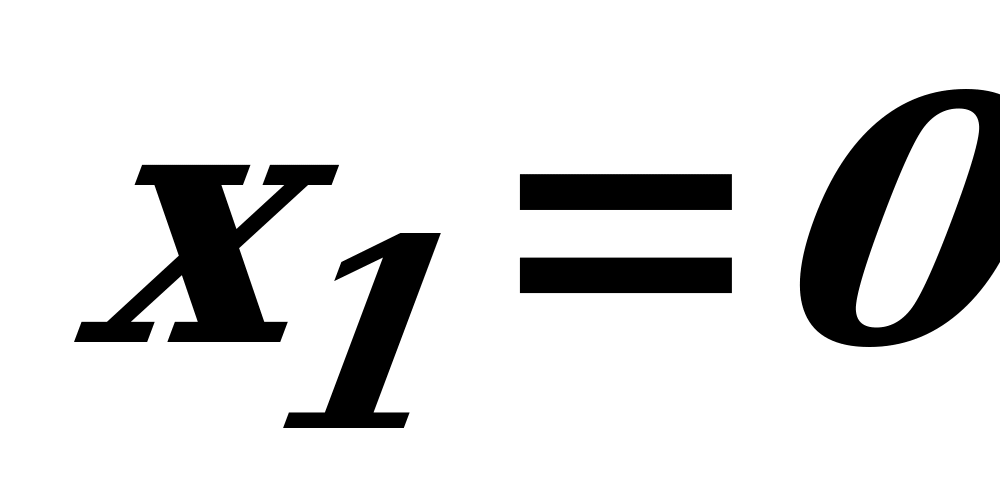 ,
, 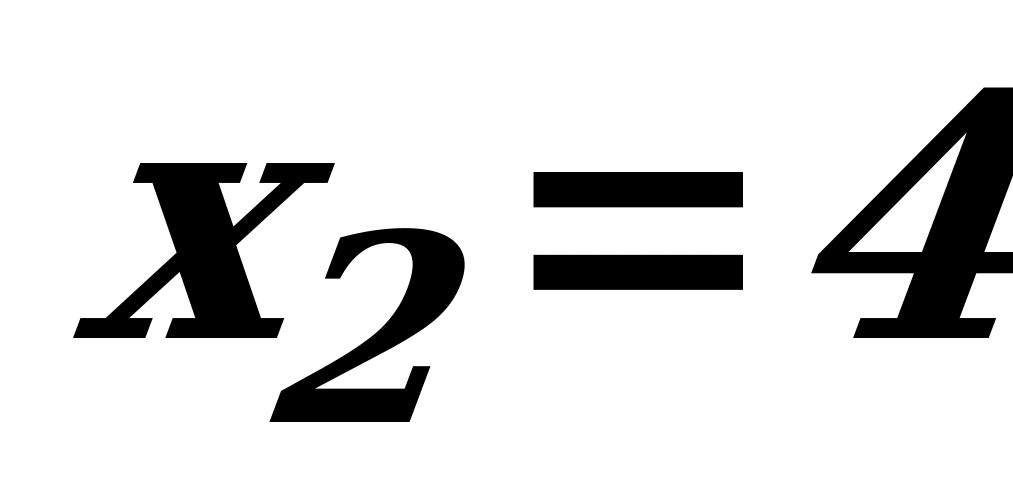 . Вычислив значения производной на отдельных интервалах, делаем относительно поведения функции заключение, проиллюстрированное рисунком;
. Вычислив значения производной на отдельных интервалах, делаем относительно поведения функции заключение, проиллюстрированное рисунком;
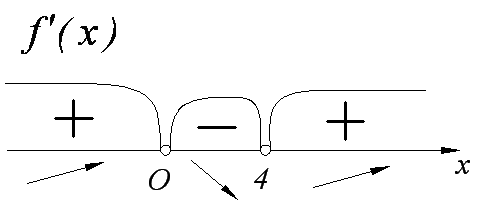
Рисунок
-
Областью определения функции 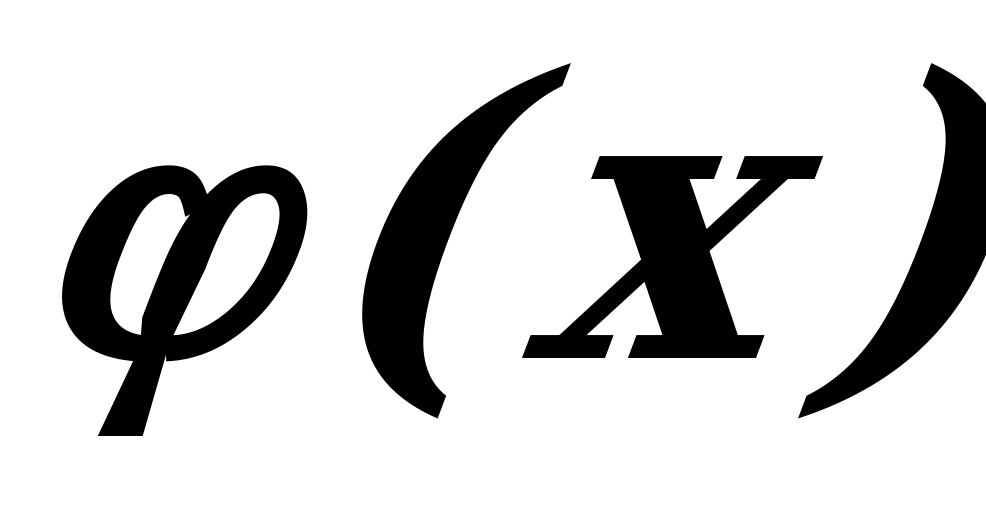 является вся числовая прямая, кроме точки
является вся числовая прямая, кроме точки 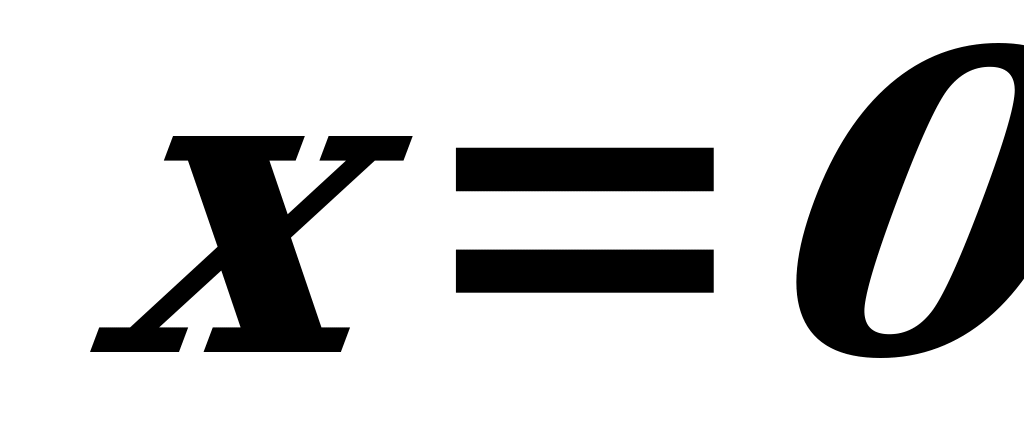 . Производная
. Производная 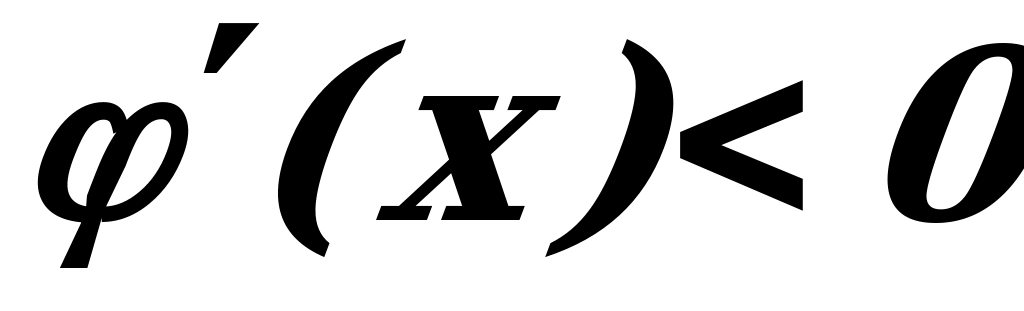 при всех значениях х из области определения функции, следовательно, функция убывает на интервалах
при всех значениях х из области определения функции, следовательно, функция убывает на интервалах 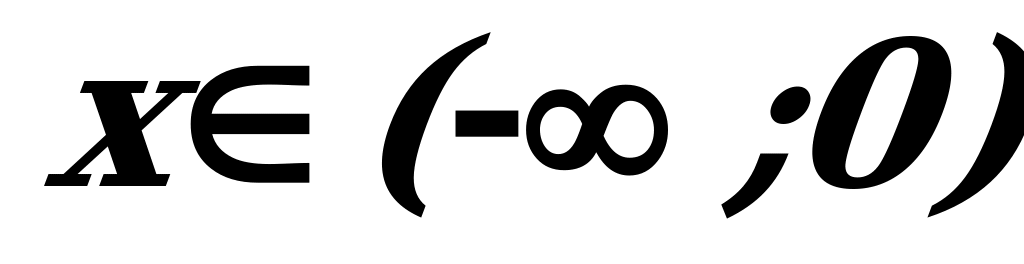
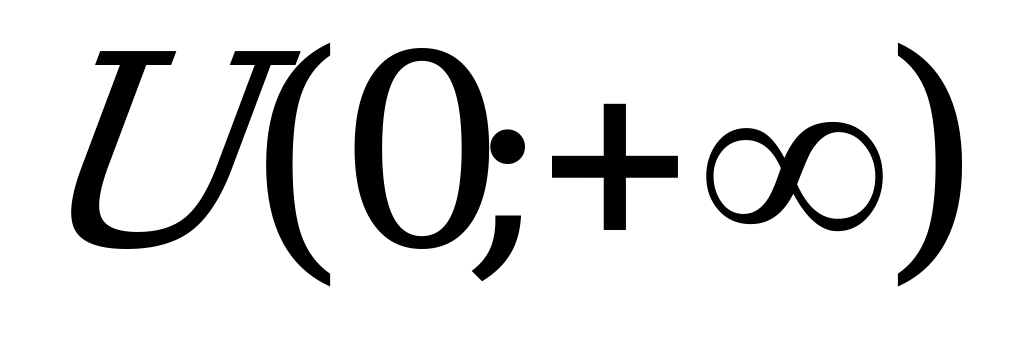 ;
;
-
Область определения функции 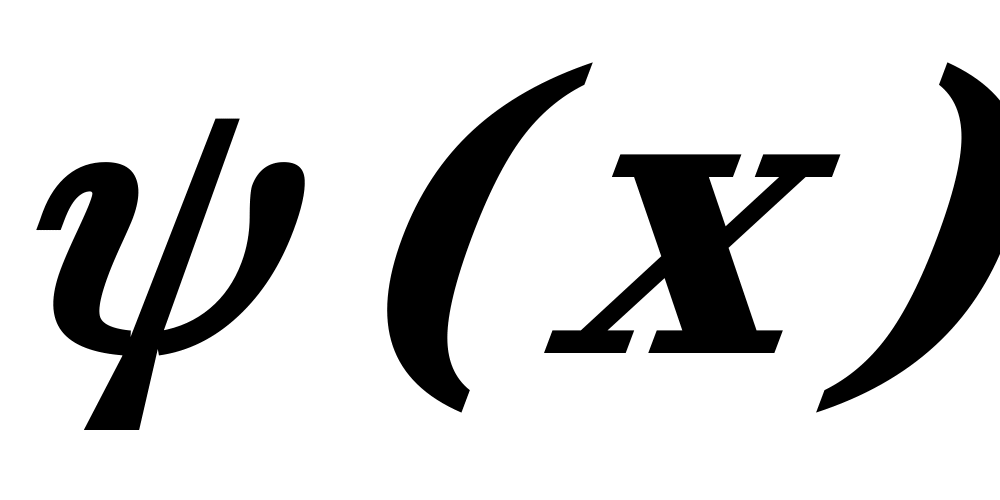 - интервал
- интервал  . Производная
. Производная 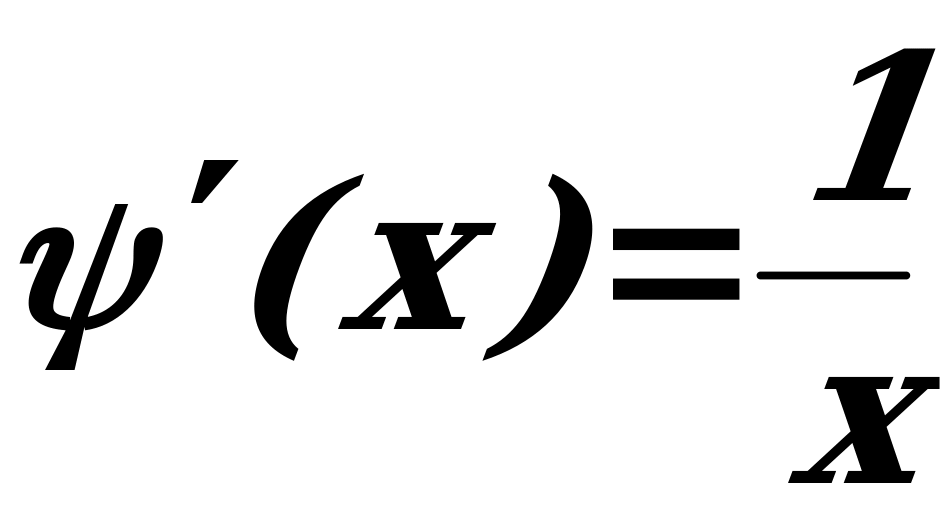 на этом интервале всегда положительна. Следовательно, функция
на этом интервале всегда положительна. Следовательно, функция 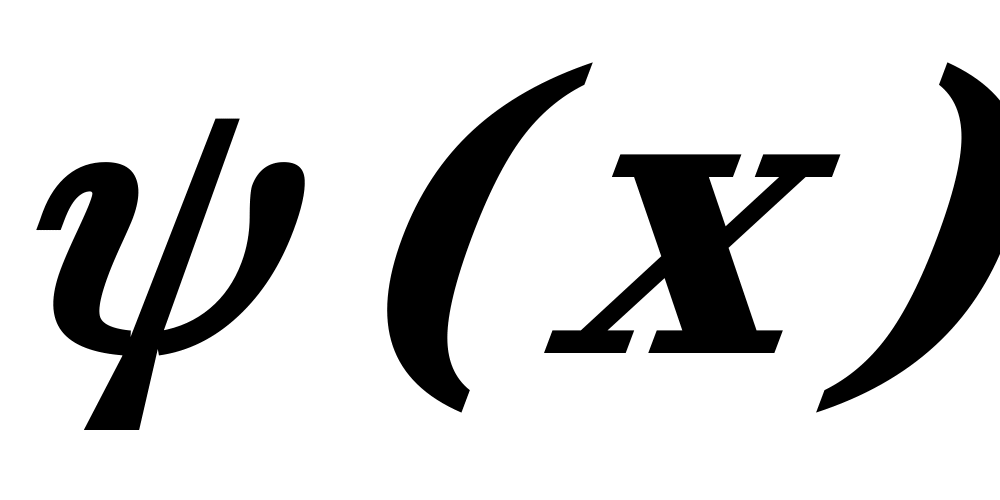 является возрастающей на всей области определения.
является возрастающей на всей области определения.
Точки минимума и точки максимума называются точками экстремума.
Если слева от некоторого допустимого значения 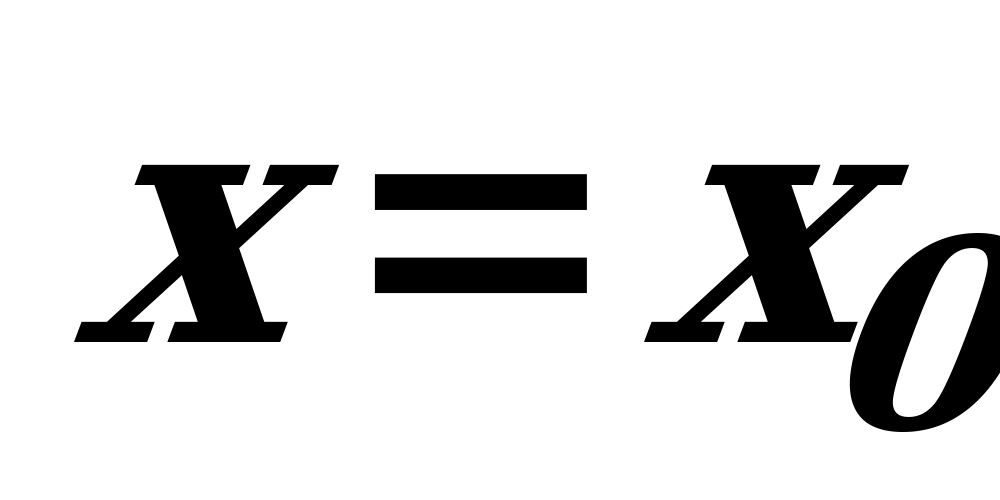 функция
функция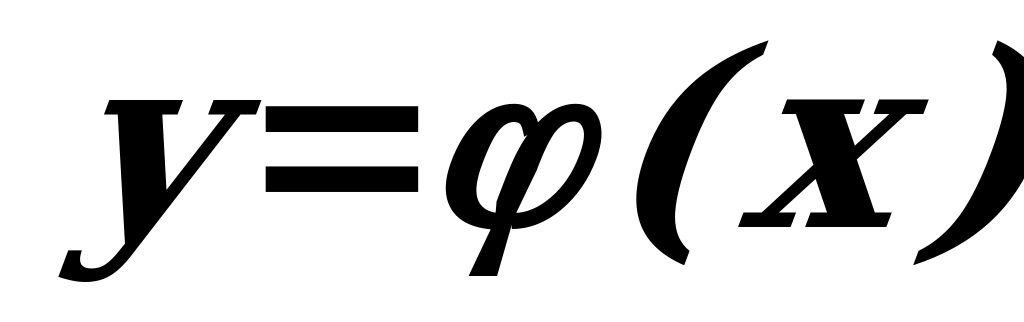 возрастает, а справа – убывает, то
возрастает, а справа – убывает, то 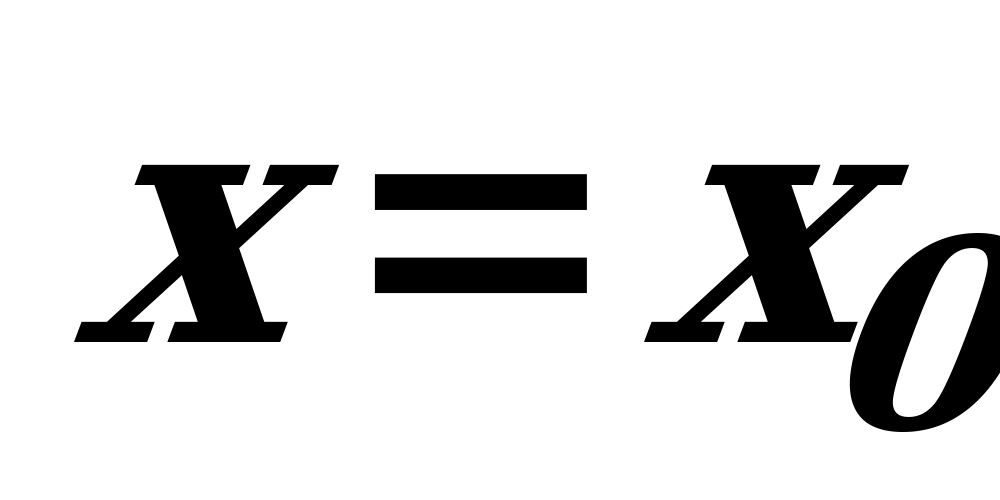 называется точкой максимума данной функции, т.е. функция
называется точкой максимума данной функции, т.е. функция 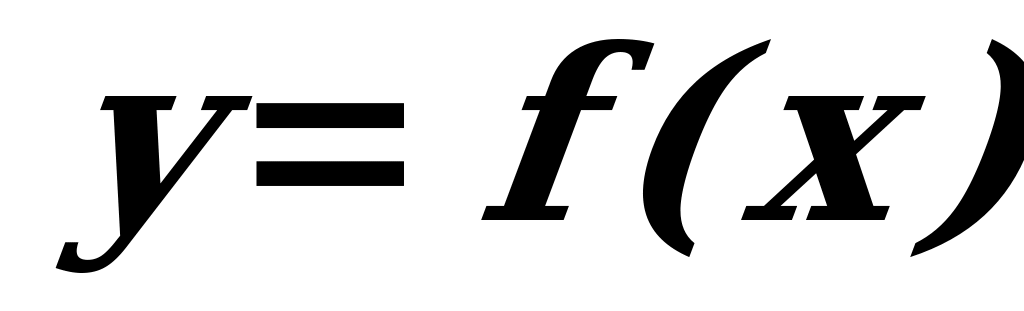 при
при 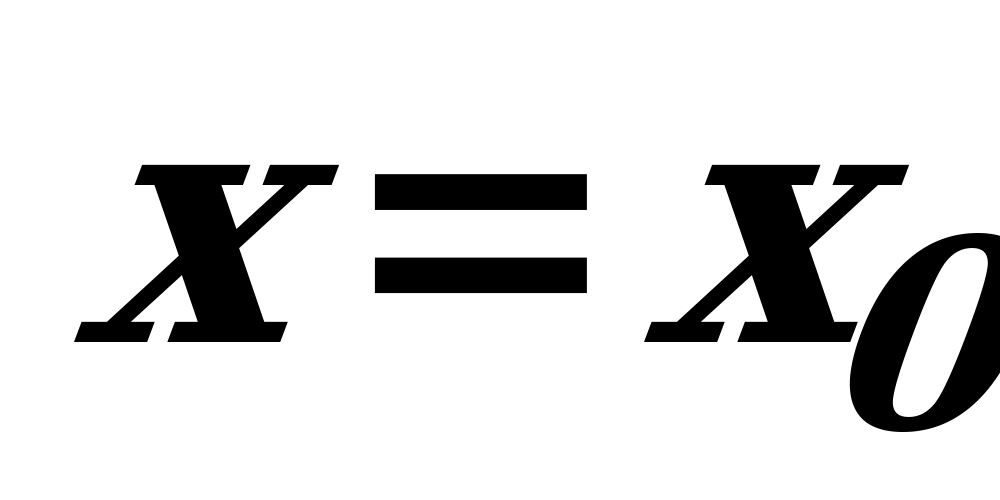 имеет максимум. Если слева от точки
имеет максимум. Если слева от точки 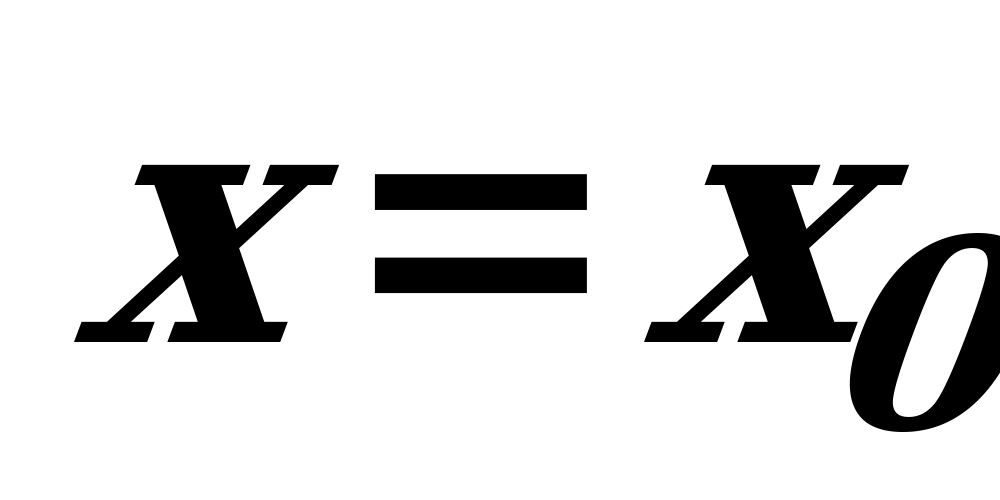 функция
функция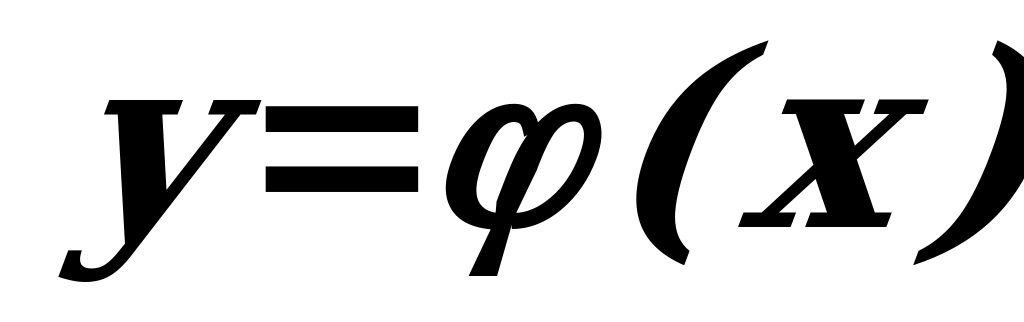 убывает, а справа – возрастает, то значение
убывает, а справа – возрастает, то значение 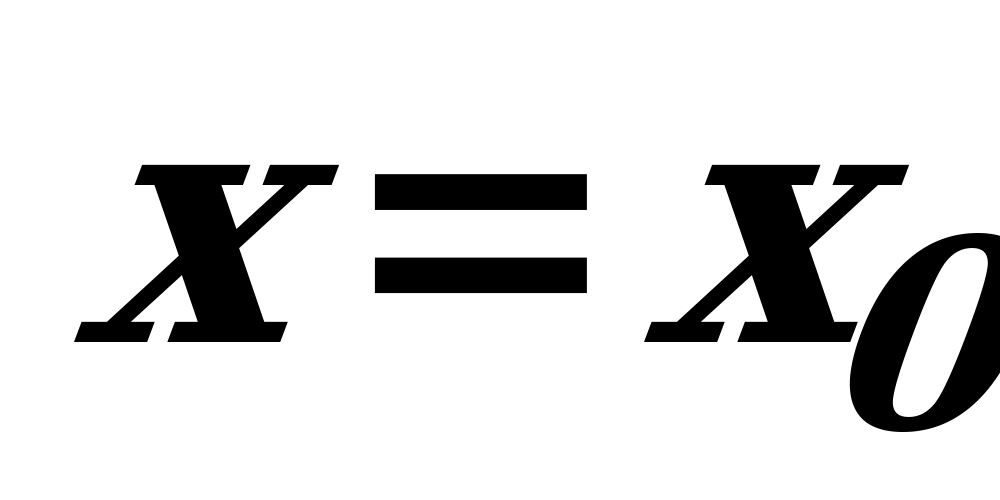 называется точкой минимума данной функции, т.е. функция
называется точкой минимума данной функции, т.е. функция 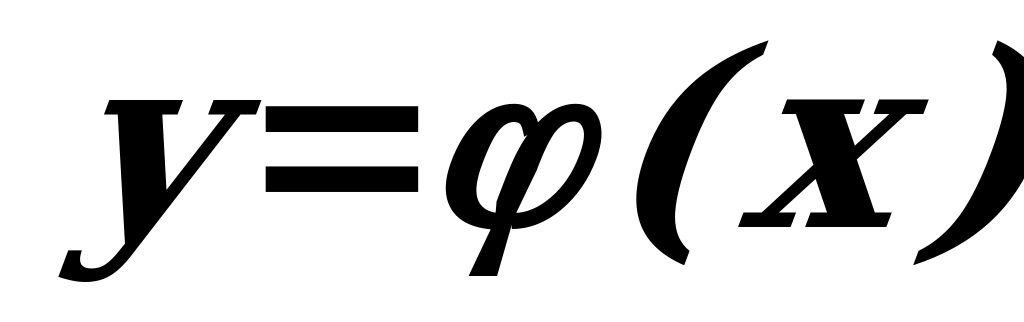 при
при 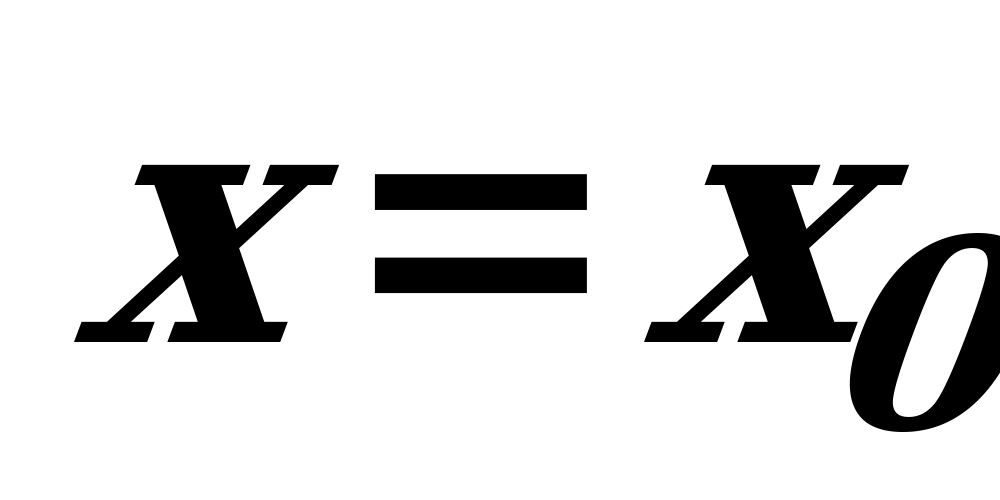 имеет минимум.
имеет минимум.
Точка максимума служит границей перехода функции от возрастания к убыванию, а точка минимума – границей перехода функции от убывания к возрастанию.
Необходимо отметить, что функция может иметь либо только один максимум (например, функция 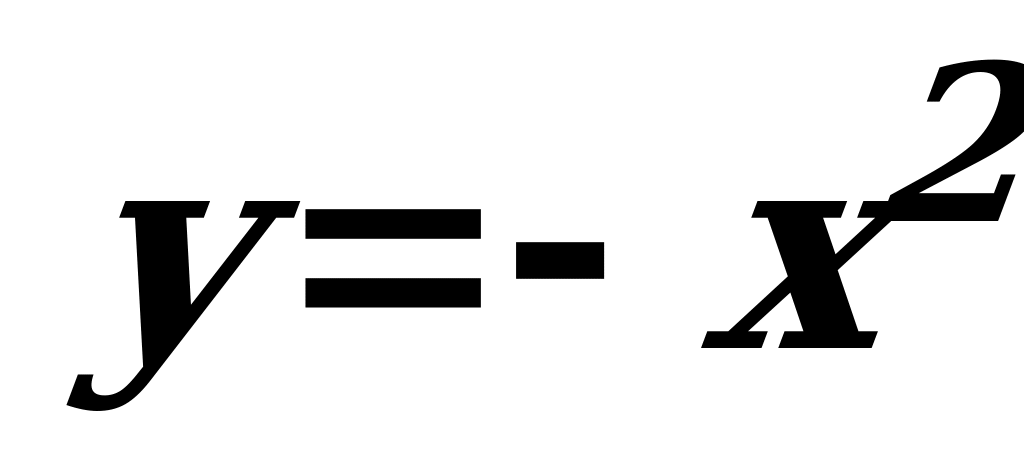 ) или только один минимум (например, функция
) или только один минимум (например, функция 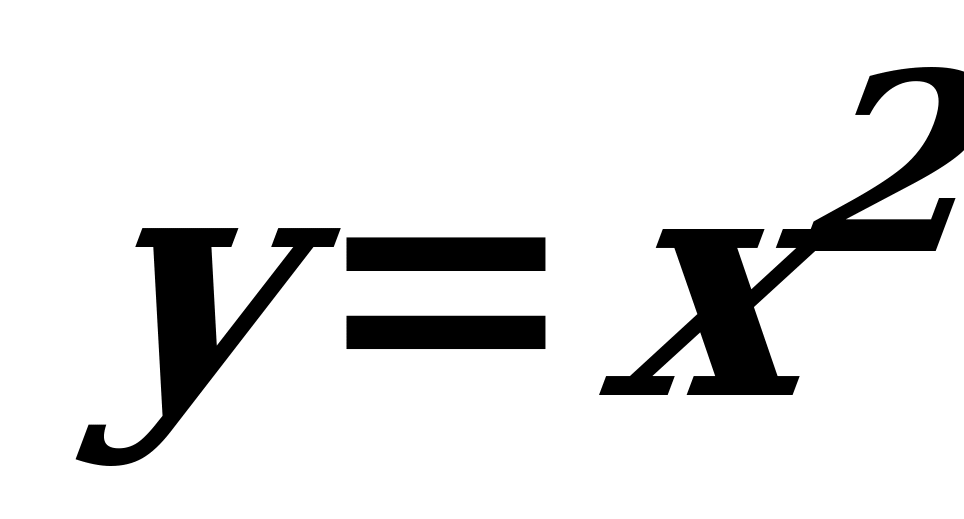 ), либо множество максимумов и минимумов (например,
), либо множество максимумов и минимумов (например,  , либо не иметь ни максимума, ни минимума (например,
, либо не иметь ни максимума, ни минимума (например, 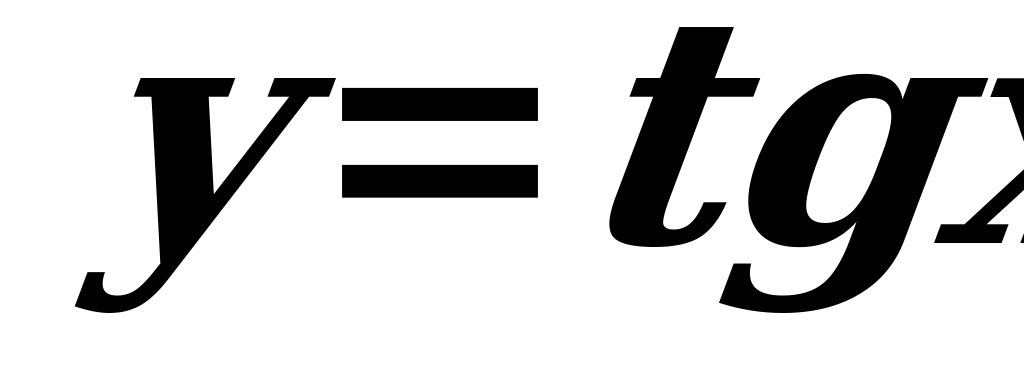 ).
).
Признаки максимума и минимума функции.
Точки, в которых производная функции равна нулю, называются стационарными.
Если при переходе через стационарную точку (такую, в которой производная функции равна нулю) 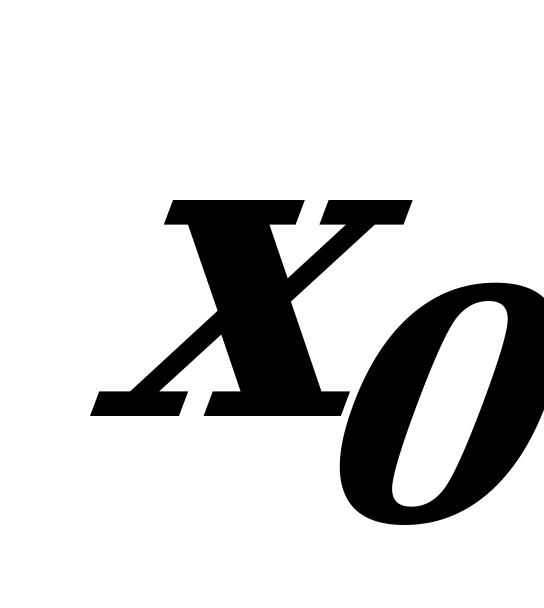 функции
функции 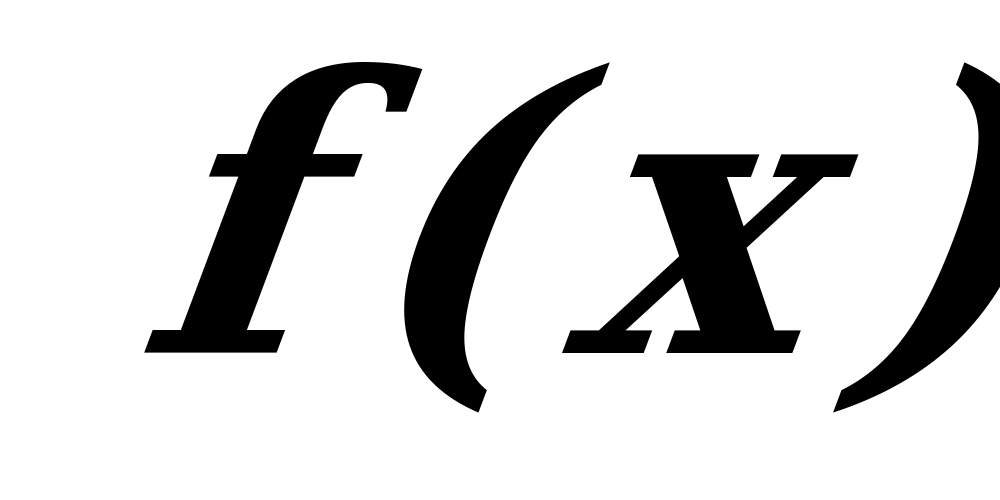 ее производная меняет знак с положительного на отрицательный, т.е. слева от точки
ее производная меняет знак с положительного на отрицательный, т.е. слева от точки 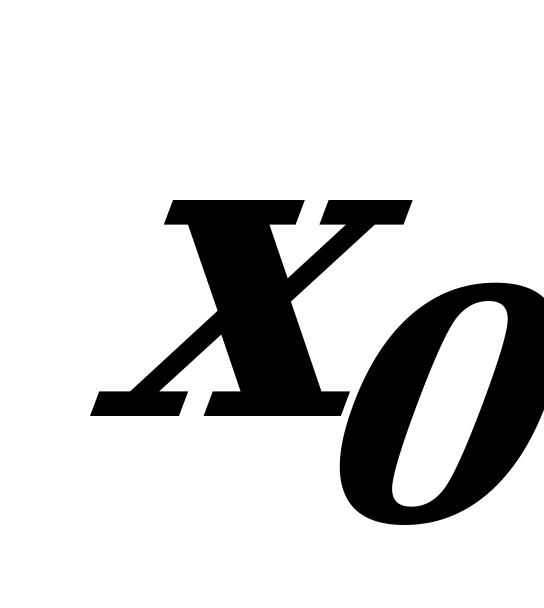 значение
значение 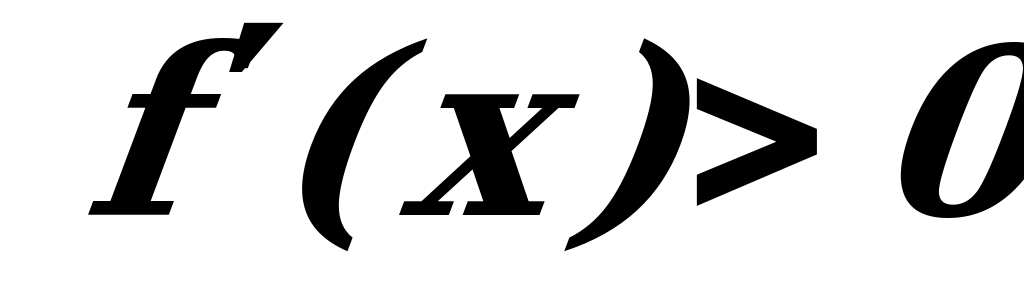 , а справа от точки
, а справа от точки 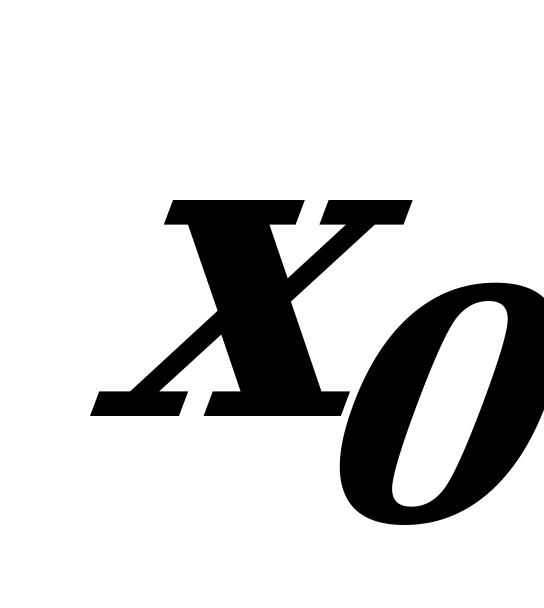 значение
значение 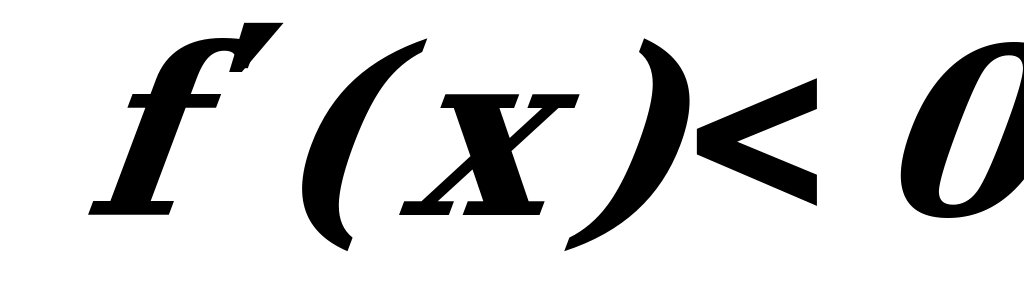 , то точка
, то точка 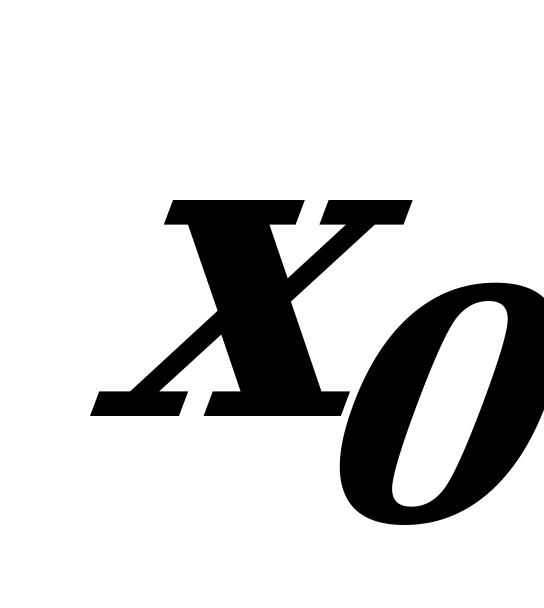 является точкой максимума функции
является точкой максимума функции 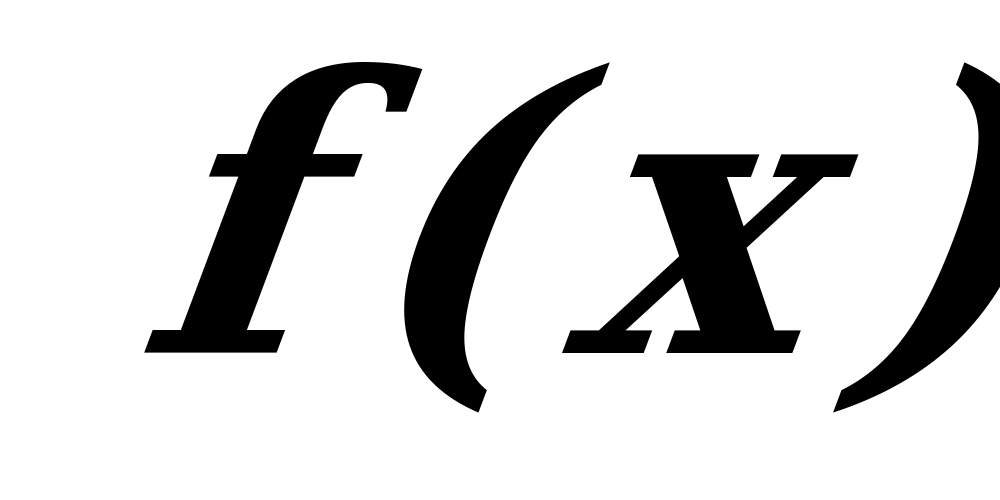 .
.
Если при переходе через стационарную точку 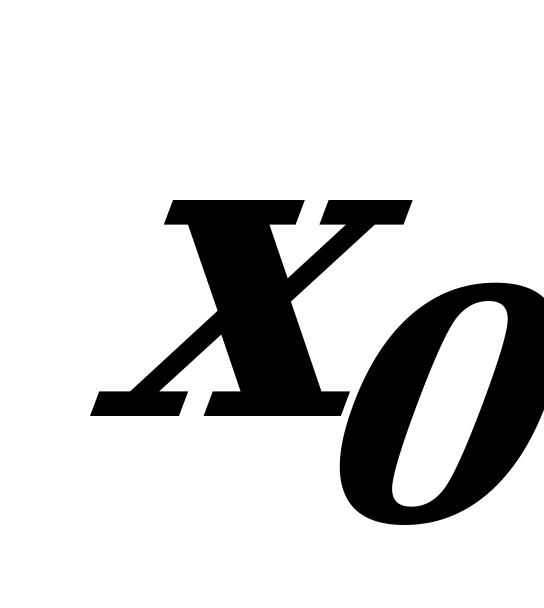 функции
функции 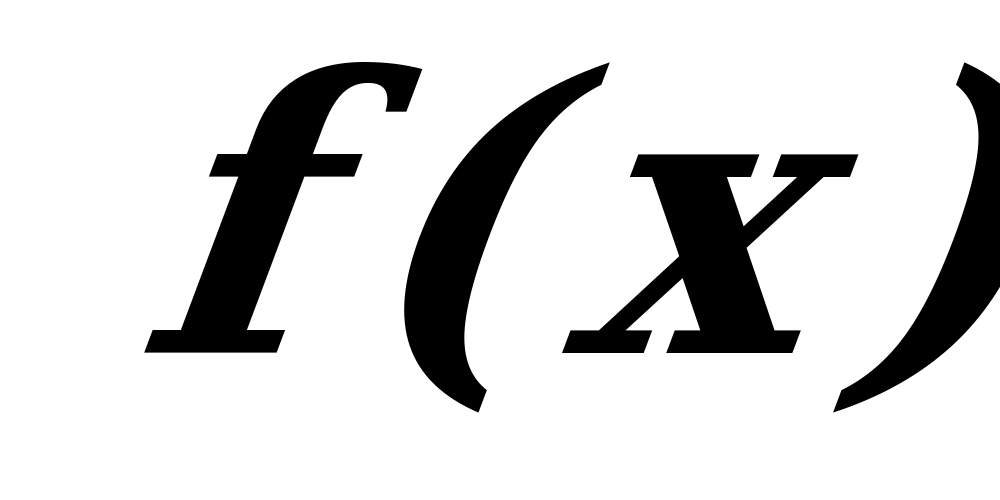 ее производная меняет знак с отрицательного на положительный, то точка
ее производная меняет знак с отрицательного на положительный, то точка 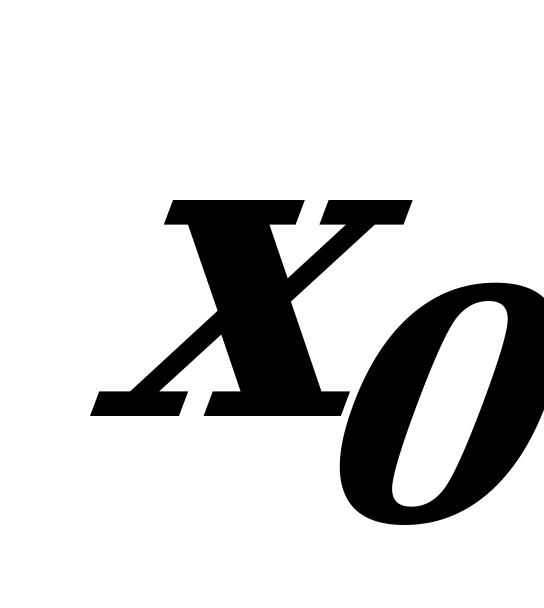 является точкой минимума функции
является точкой минимума функции 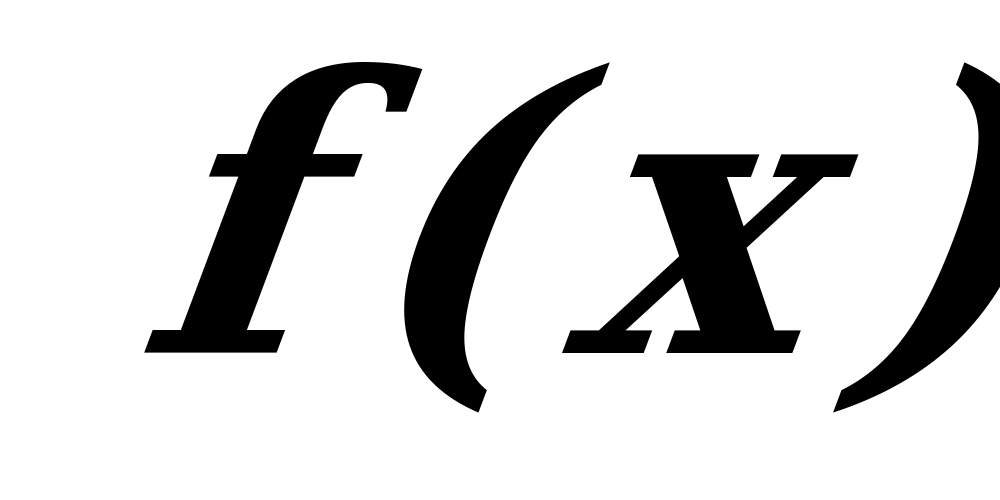 .
.
Признаки экстремума функции являются необходимыми и достаточными.
Отметим, что функция может имеет экстремум в точке, в которой эта функция не имеет производной (в качестве примера можно указать функцию 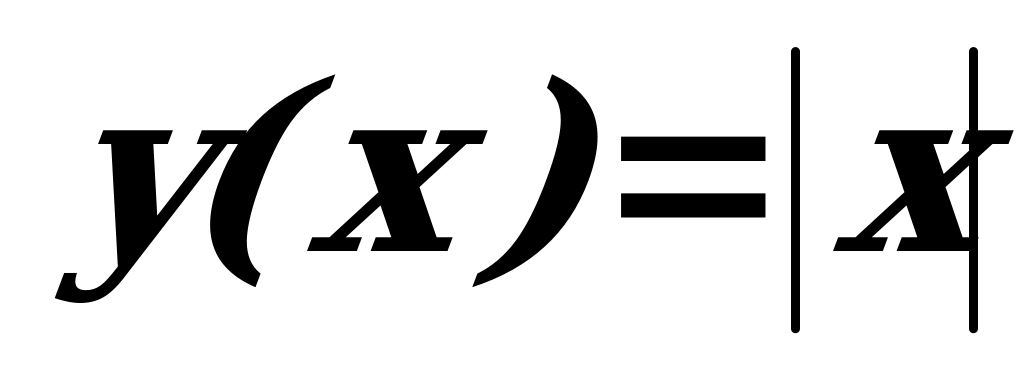 ;
; 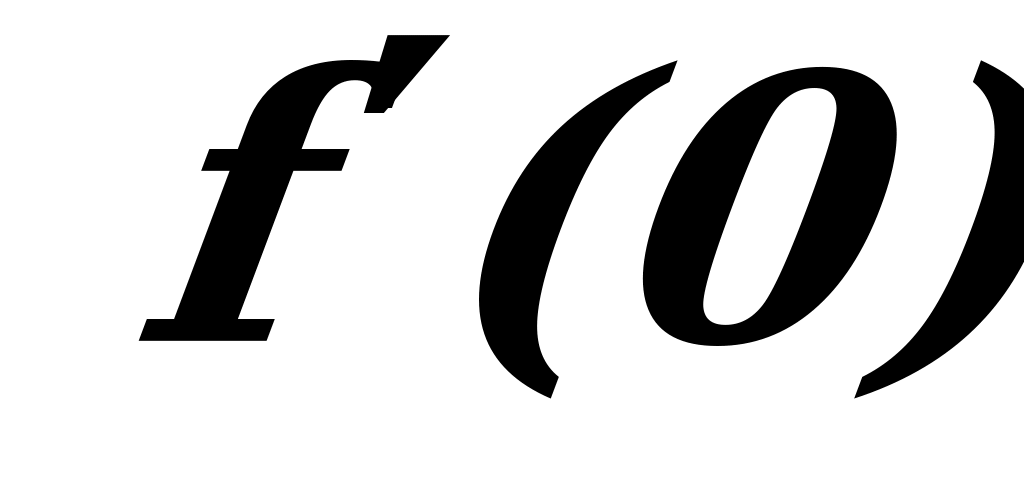 не существует;
не существует; 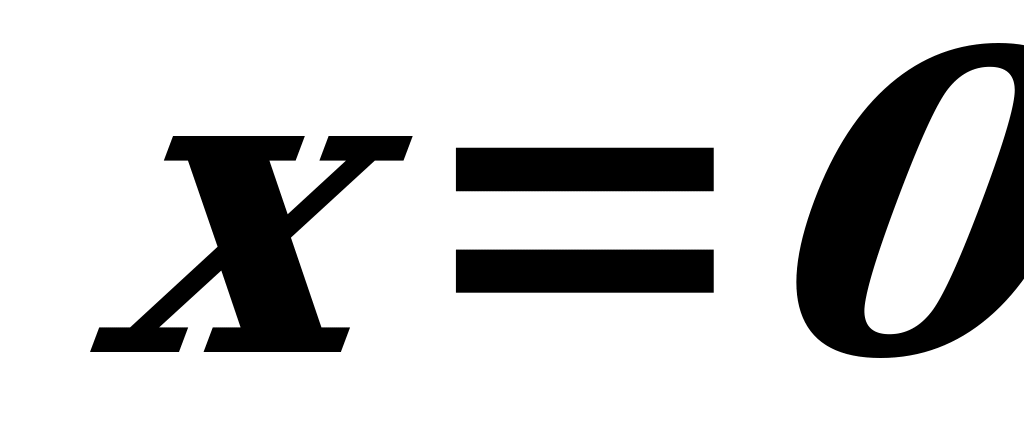 - точка минимума функции). Стационарные точки, а также такие, в которых функция не имеет производной, в совокупности называются критическими точками этой функции.
- точка минимума функции). Стационарные точки, а также такие, в которых функция не имеет производной, в совокупности называются критическими точками этой функции.
Существуют функции, в которых первая производная, обращаясь в нуль при 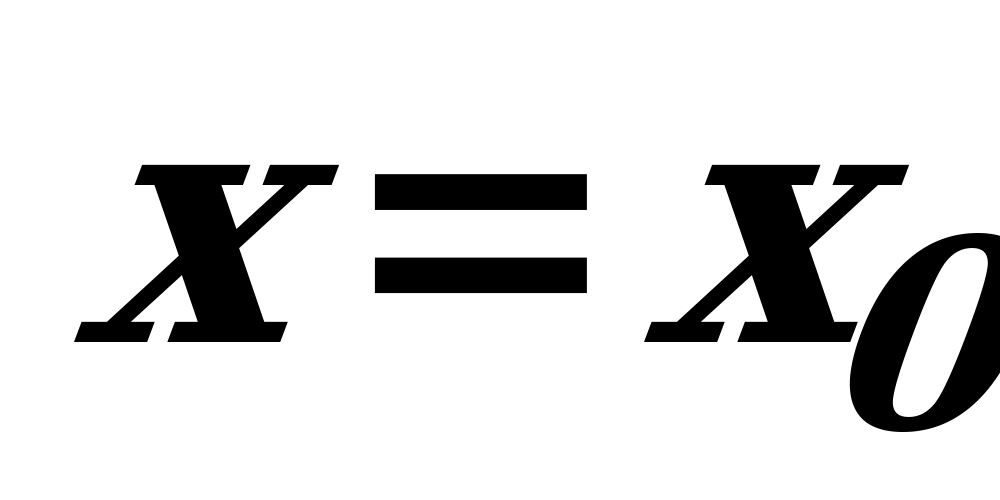 , не меняет знака при переходе аргумента через
, не меняет знака при переходе аргумента через 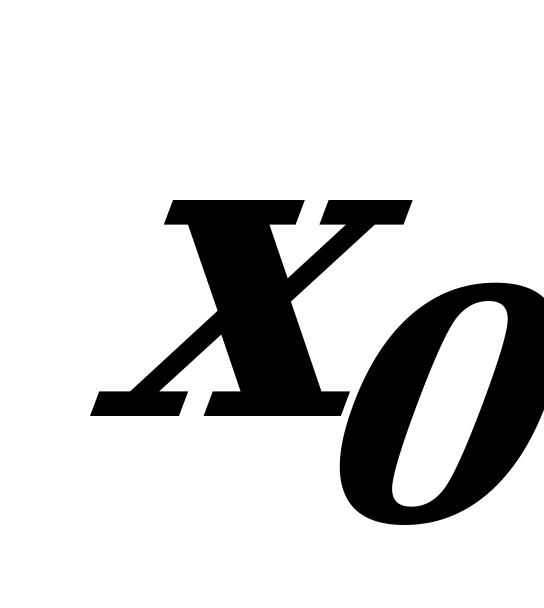 . В таком случае функция в этой точке не имеет экстремума.
. В таком случае функция в этой точке не имеет экстремума.
Практические правила исследования функции на максимум и минимум с помощью первой производной. Необходимо придерживаться следующего алгоритма:
-
Найти производную 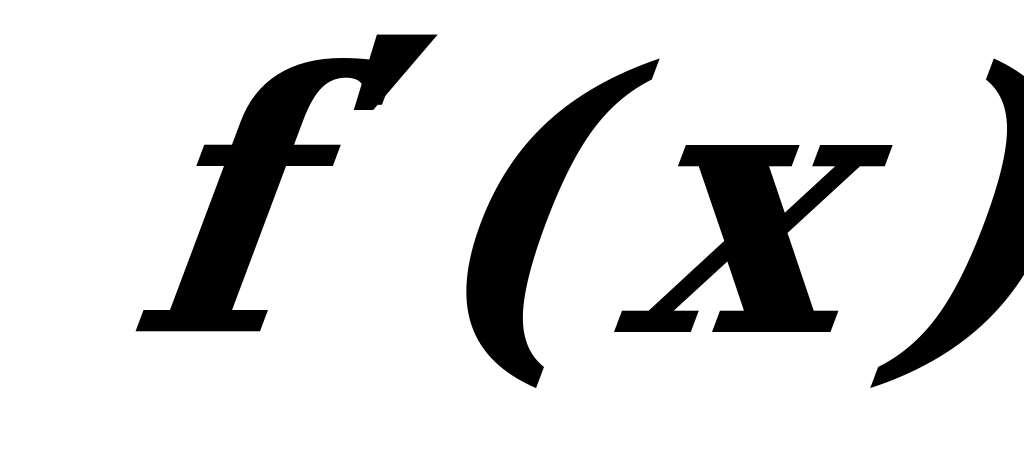 функции
функции 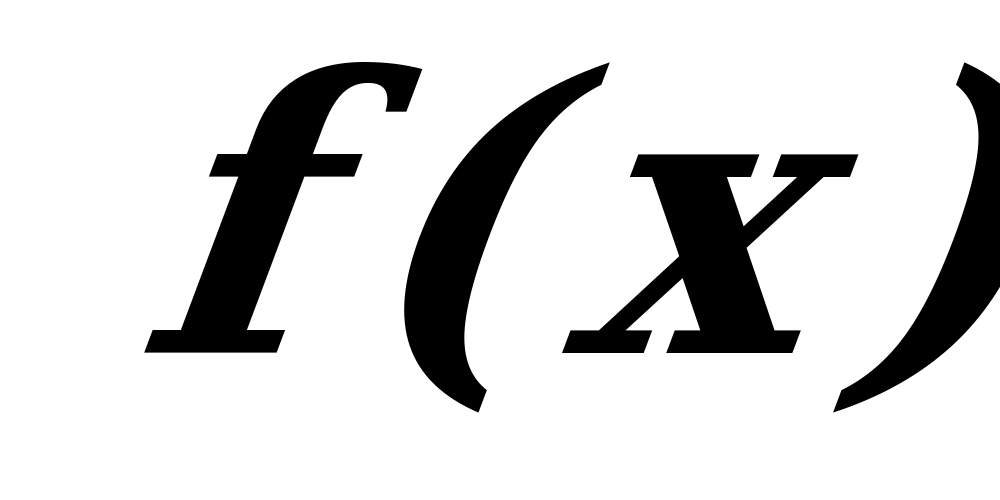 .
.
-
Найти критические точки функции 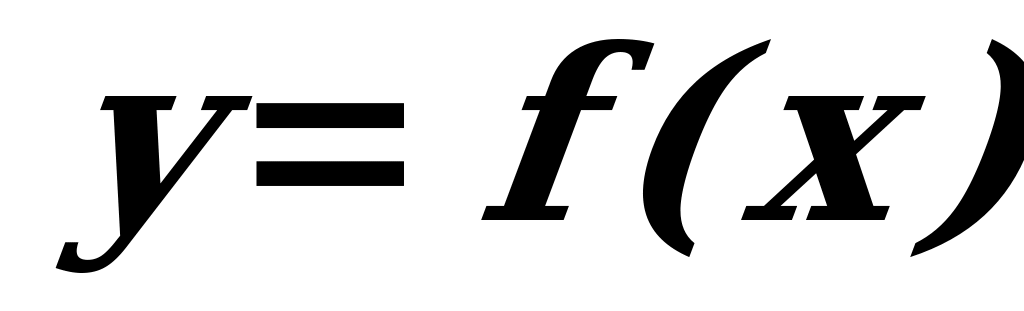 , т.е. точки, в которых
, т.е. точки, в которых 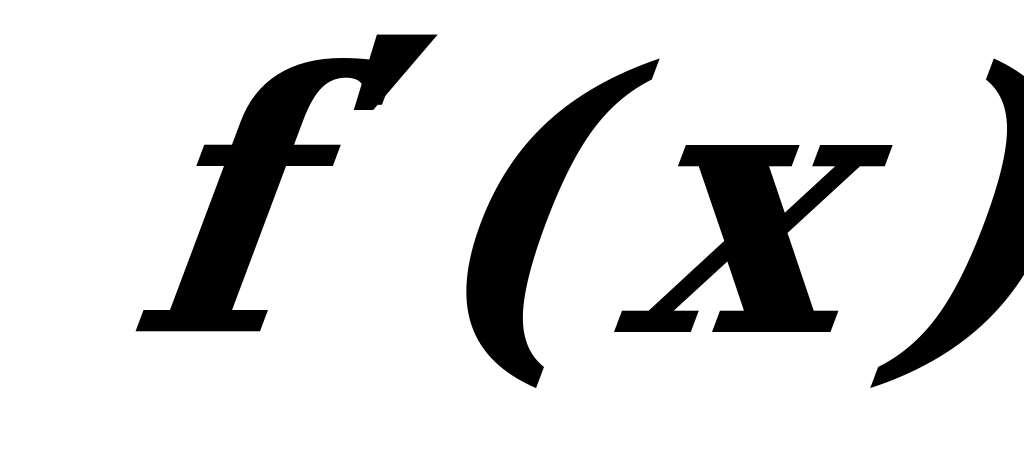 обращается в нуль.
обращается в нуль.
-
Исследовать знак производной 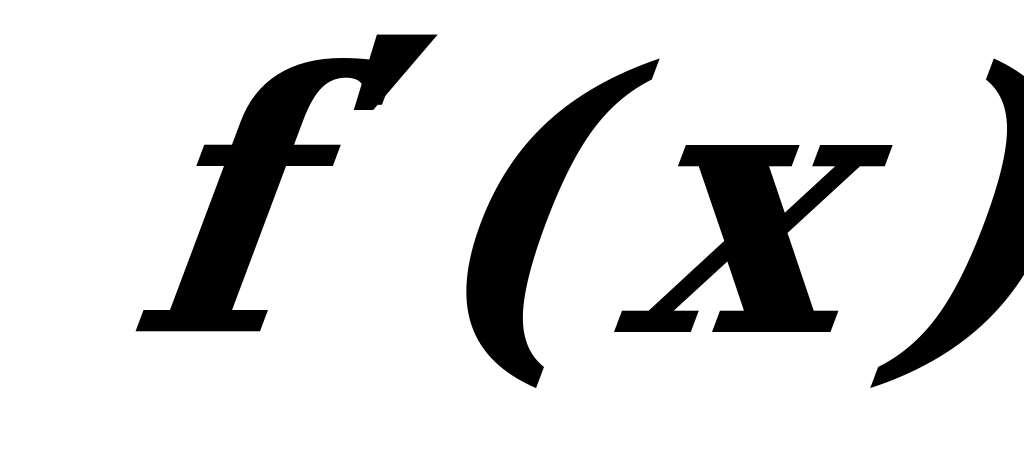 . При этом критическая точка
. При этом критическая точка 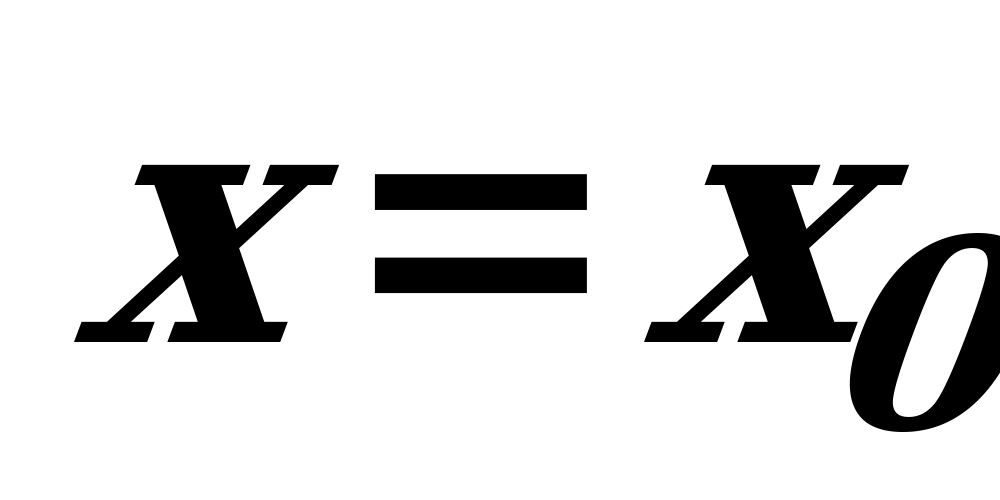 есть точка минимума или максимума (в зависимости от ситуации), если производная меняет знак при переходе через
есть точка минимума или максимума (в зависимости от ситуации), если производная меняет знак при переходе через 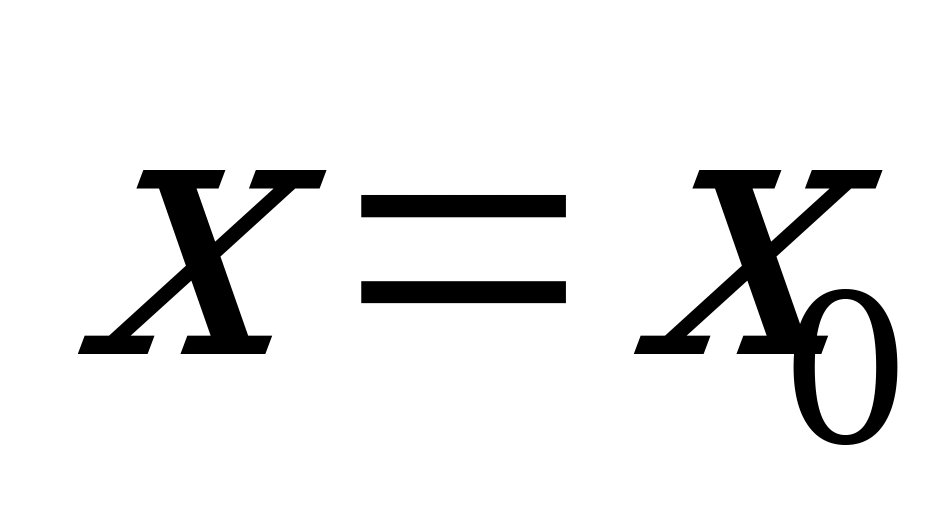 . Если же в соседних промежутках, разделенных критической точкой
. Если же в соседних промежутках, разделенных критической точкой 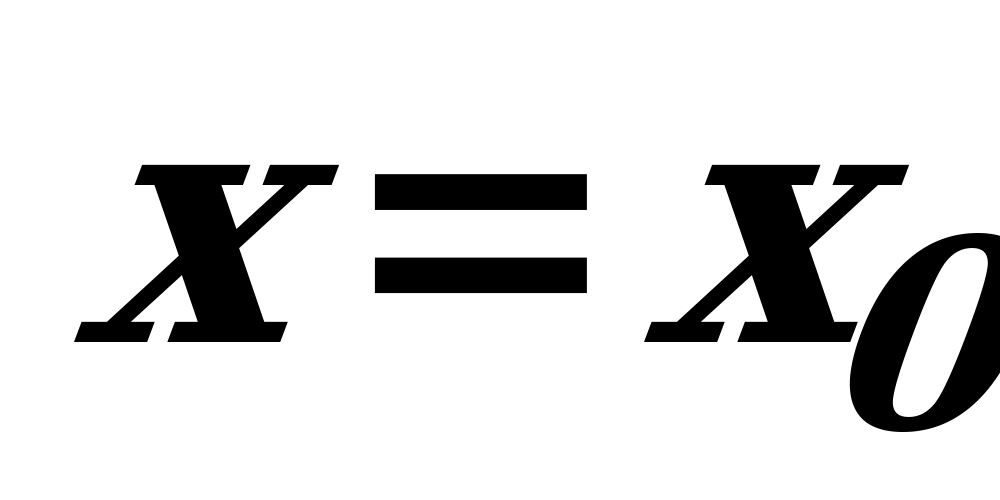 , знак производной не меняется, то в точке
, знак производной не меняется, то в точке 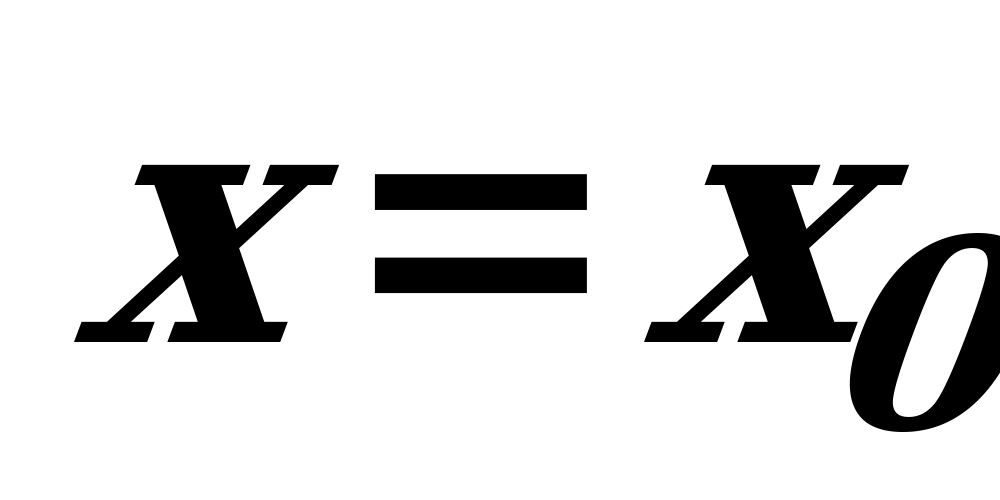 функция не имеет ни максимума, ни минимума.
функция не имеет ни максимума, ни минимума.
-
Вычислить значения функции в точках максимума и минимума (вычислить f(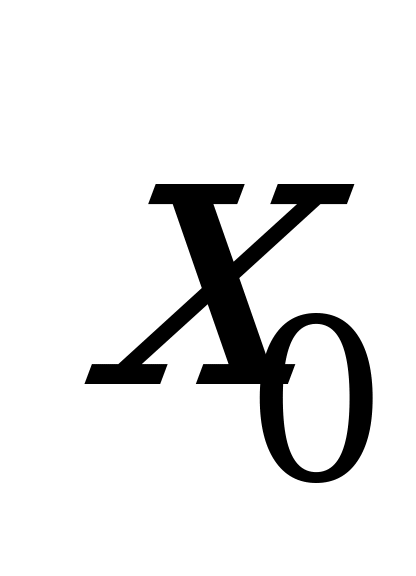 ))
))
Пример.
Исследовать на экстремум функцию:
1) 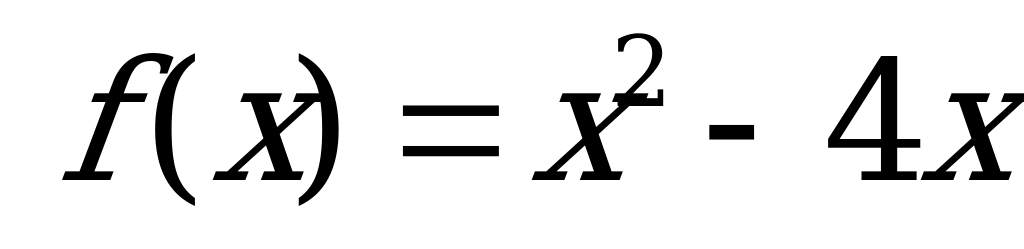 ;
;
2) 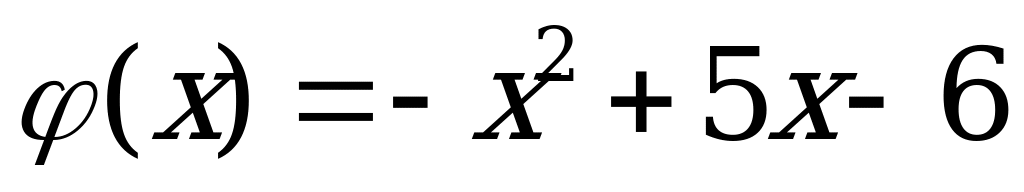 ;
;
3) 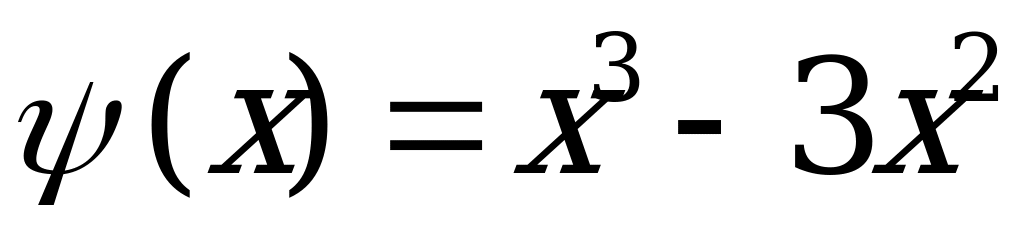 .
.
Решение
-
Находим 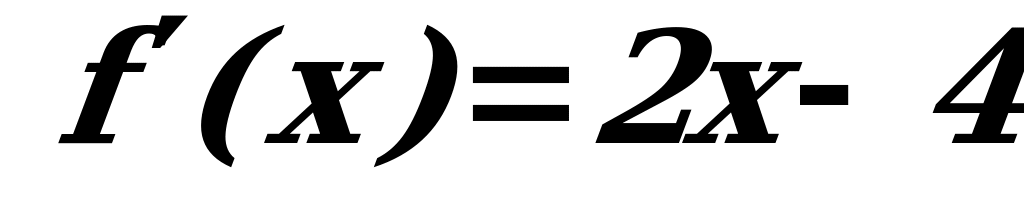 .
.
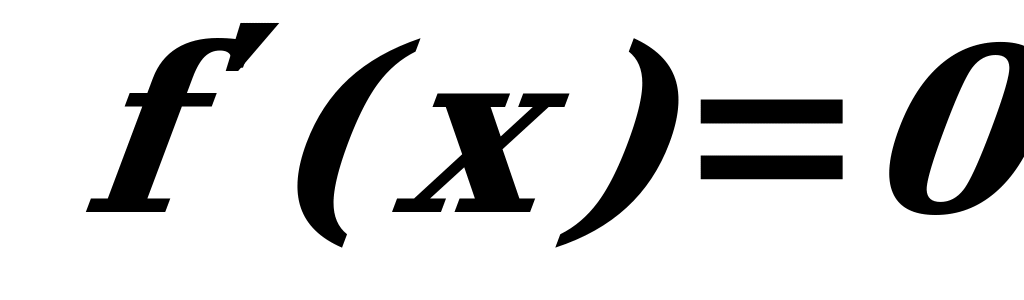 , =2x-4 = 0=
, =2x-4 = 0= 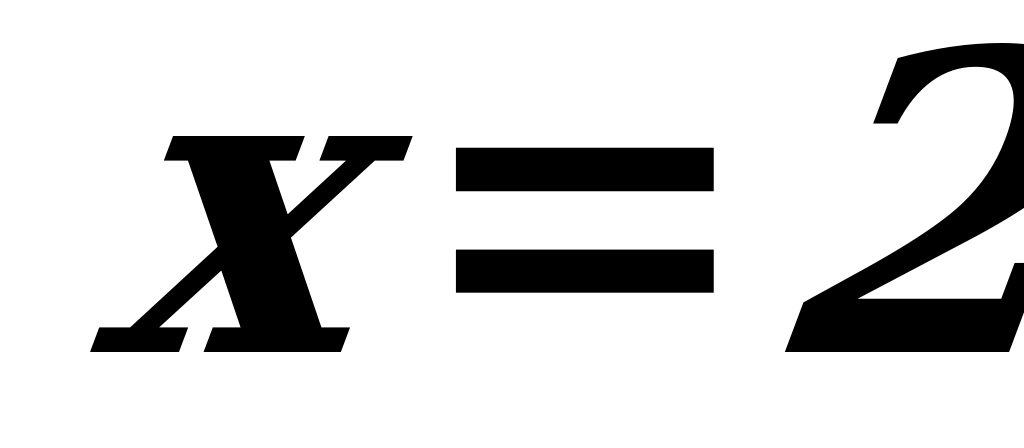 - критическая точка
- критическая точка
-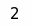
+
Слева от точки
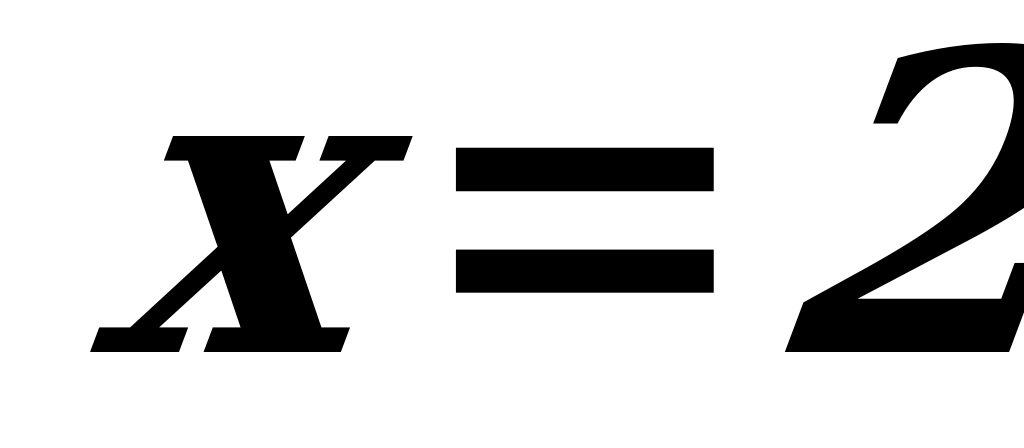
производная
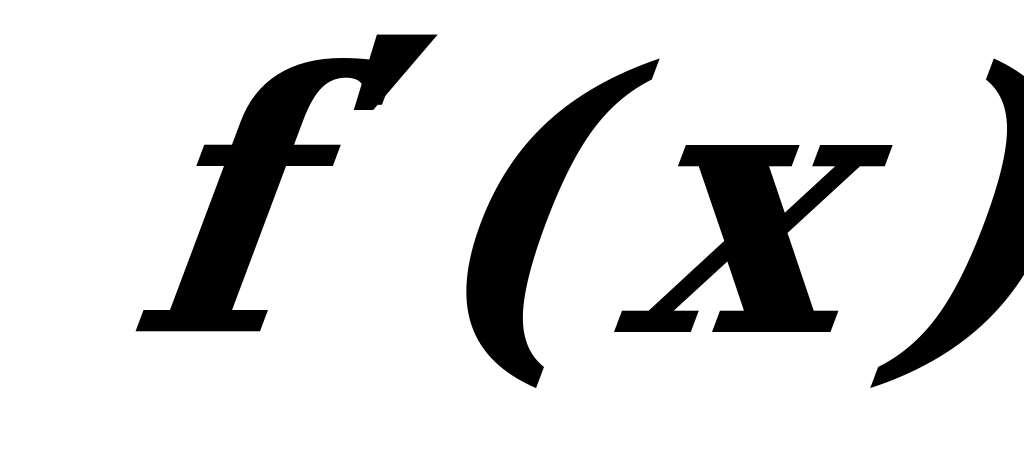
имеет отрицательные значения, справа – положительные
(подставим 0: 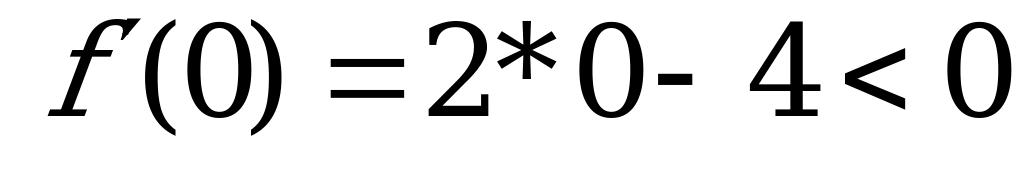 ).
).
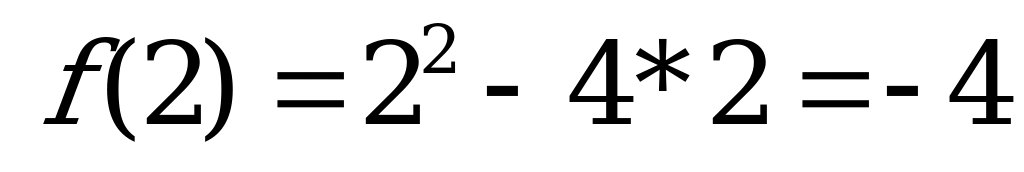

2
х

min
Ответ: т. min ( 2; -4)
-
Находим 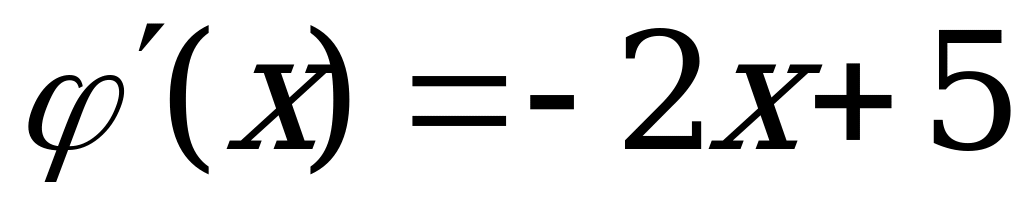 .
.
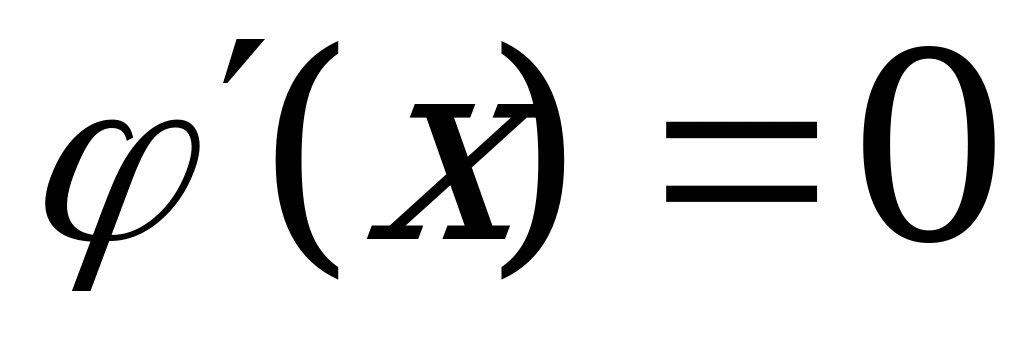 =
= 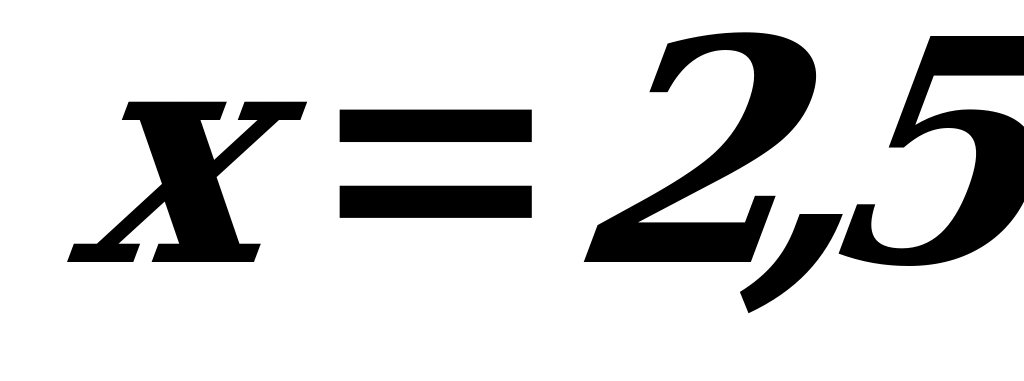 - критическая точка
- критическая точка
Чтобы выяснить знаки подставим 0:
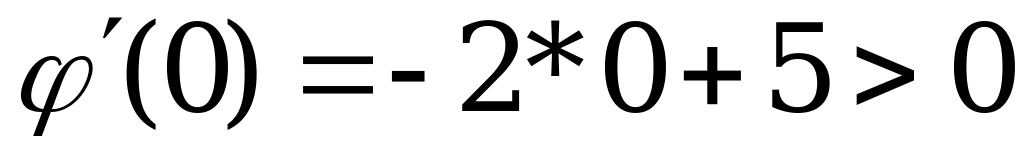
+
-
(имеем слева от 2,5 знак +)
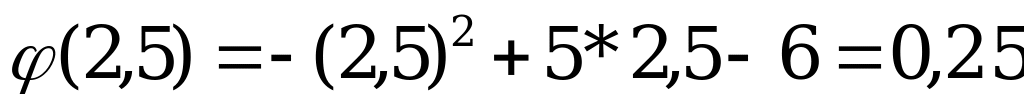

2,5
х

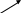
max
Ответ: т. max (2,5; 0,25)
-
Находим 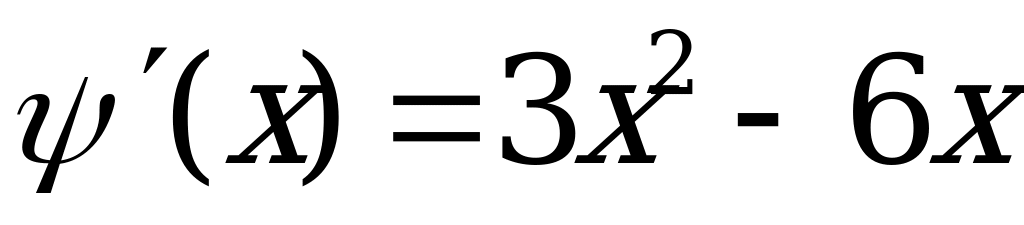 .
.
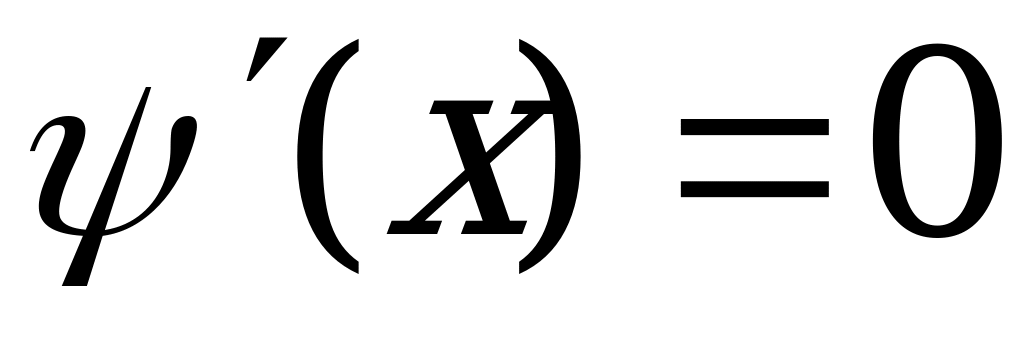 =
= 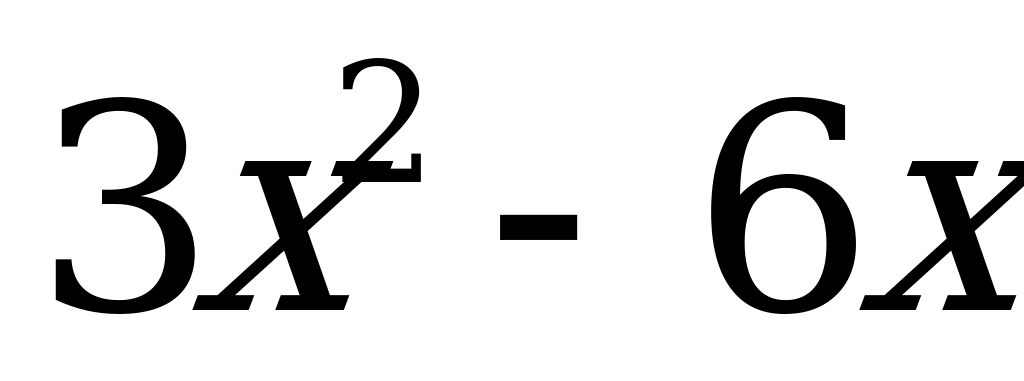 = 0 =
= 0 = 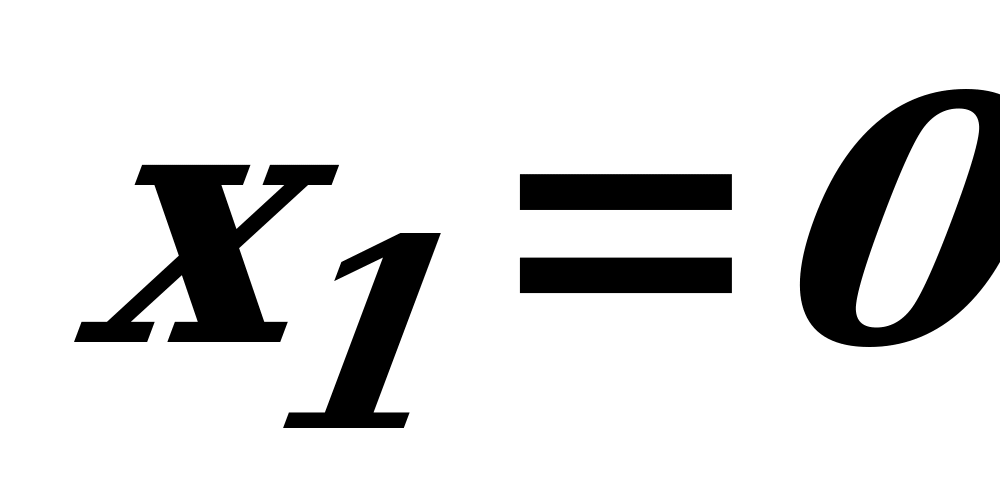 ,
, 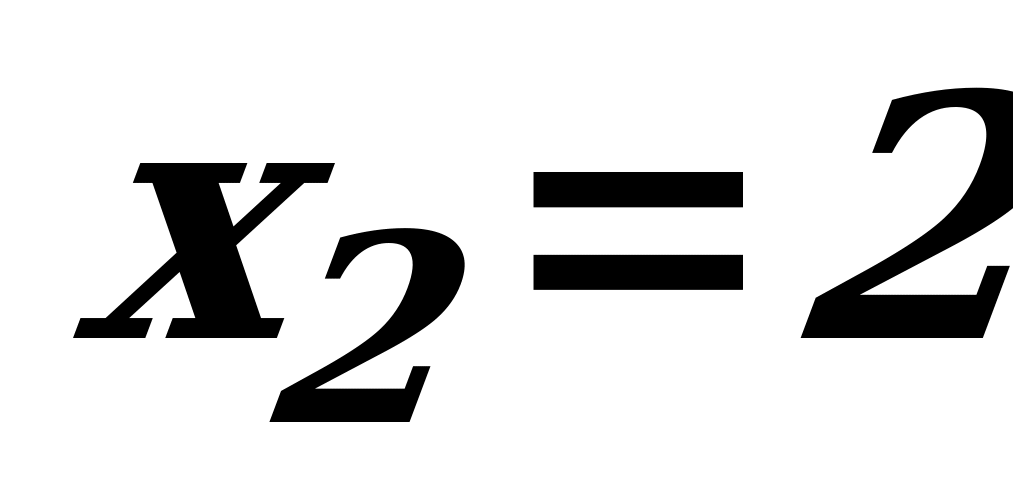 - критические точки
- критические точки
+
-
+
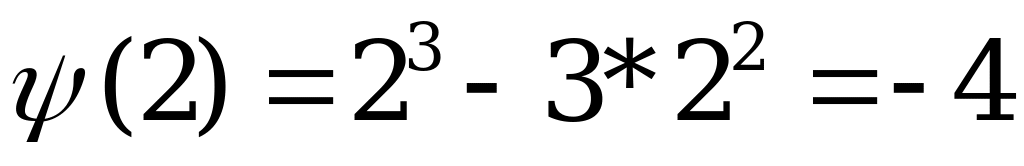
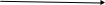

0
х
max

2
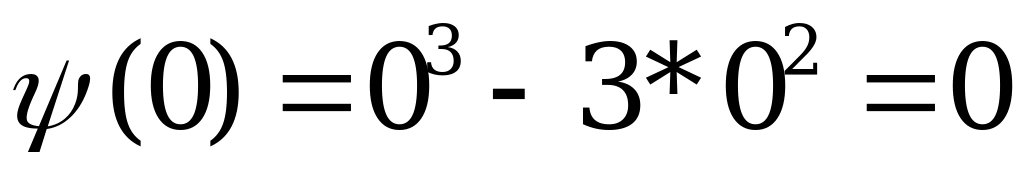
min
(так как мы находим знаки производной, то легко заметить, что графиком 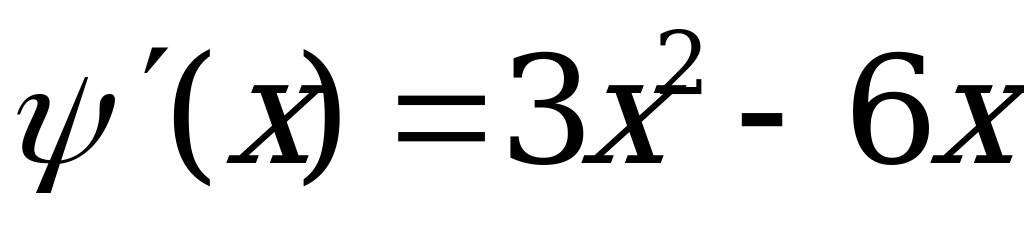 - есть парабола, ветвями вверх, по этому знаки + - + )
- есть парабола, ветвями вверх, по этому знаки + - + )
Ответ: т. max (0, 0); т. min (2, -4)