Вычисление арифметических выражений. Хранение двоичного дерева в массиве

41-42 урок, 11 класс – практика

Учитель: Брух Т.В.

Дата:____________

Тема урока: «Вычисление арифметических выражений.

Хранение двоичного дерева в массиве»

Ход урока:

1. Организационный момент

2. Проверка домашнего задания

- кратчайший путь, порядок графа, размер

- Сообщение А4, тема: "Использование графов для анализа данных в Интернете" - защита сообщения

3. Самостоятельная работа

- презентация графы2

- практическая работа с графами

4. Изучение нового материала

Презентация

Деревья

Вы уже знакомы с понятием «генеалогическое древо». Рассмотрим, как структура дерева влияет на действия с информацией.

Иногда нам необходимо использовать данные, между которыми есть определённые иерархические связи. В этом случае используют специальную модель — дерево. Примером такой модели выступает генеалогическое древо. В нём чётко прослеживаются связи между отдельными элементами.

Дерево — многоуровневая структура данных с четко выраженной иерархией.

Такую структуру вы не раз видели в файловых менеджерах — так называемое дерево каталогов.

По структуре дерево очень напоминает граф, потому что также состоит из узлов, связанных между собой. Самый верхний узел — корень, от него отходят ветви. Узлы, из которых не выходят ветви, называются листьями. Узлы между корнем и листьями называются внутренними узлами.

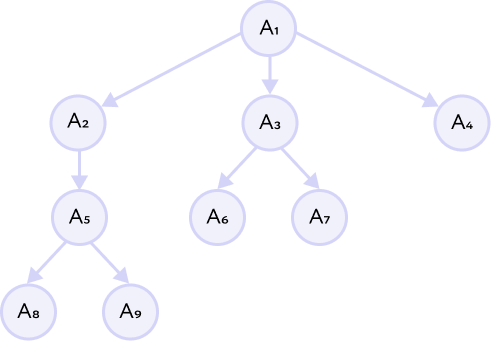
Вопрос. В указанном дереве определите корень, листья и внутренние узлы.

Ответ

 Корень — А1, листья — А8, А9, А6, А7, А4, внутренние узлы — А2, А3, А5.

На примере изображённого дерева введём ещё несколько понятий. Если внимательно посмотреть на иллюстрацию, то легко заметить, что часть А2-А5-А8-А9 можно рассмотреть как дерево с корнем А2. Эту часть дерева можно считать поддеревом.

Перемещаясь по дереву от корня А1 к различным листьям, мы будем проходить определённый путь. Самый длинный путь составит высоту дерева. Если рассматривать расположение элементов друг относительно друга, то узлы, находящиеся выше, будут предками узлов, находящихся ниже. Узлы, находящиеся ниже предка, называются потомками.

Поддерево — фрагмент дерева, который сам является деревом.

Путь — последовательность связанных между собой узлов.

Высота дерева — самая длинная последовательность узлов от корня до листа.

Предок — узел верхнего уровня.

Потомок — узел нижнего уровня.

Чаще всего деревья используют, чтобы визуализировать различные классификации в любых предметных областях. Деревья могут быть оформлены в виде схемы или списка. 

На уроках математики вы уже работали с такими моделями, когда определяли количество различных чисел, запись которых возможна с помощью нескольких цифр.

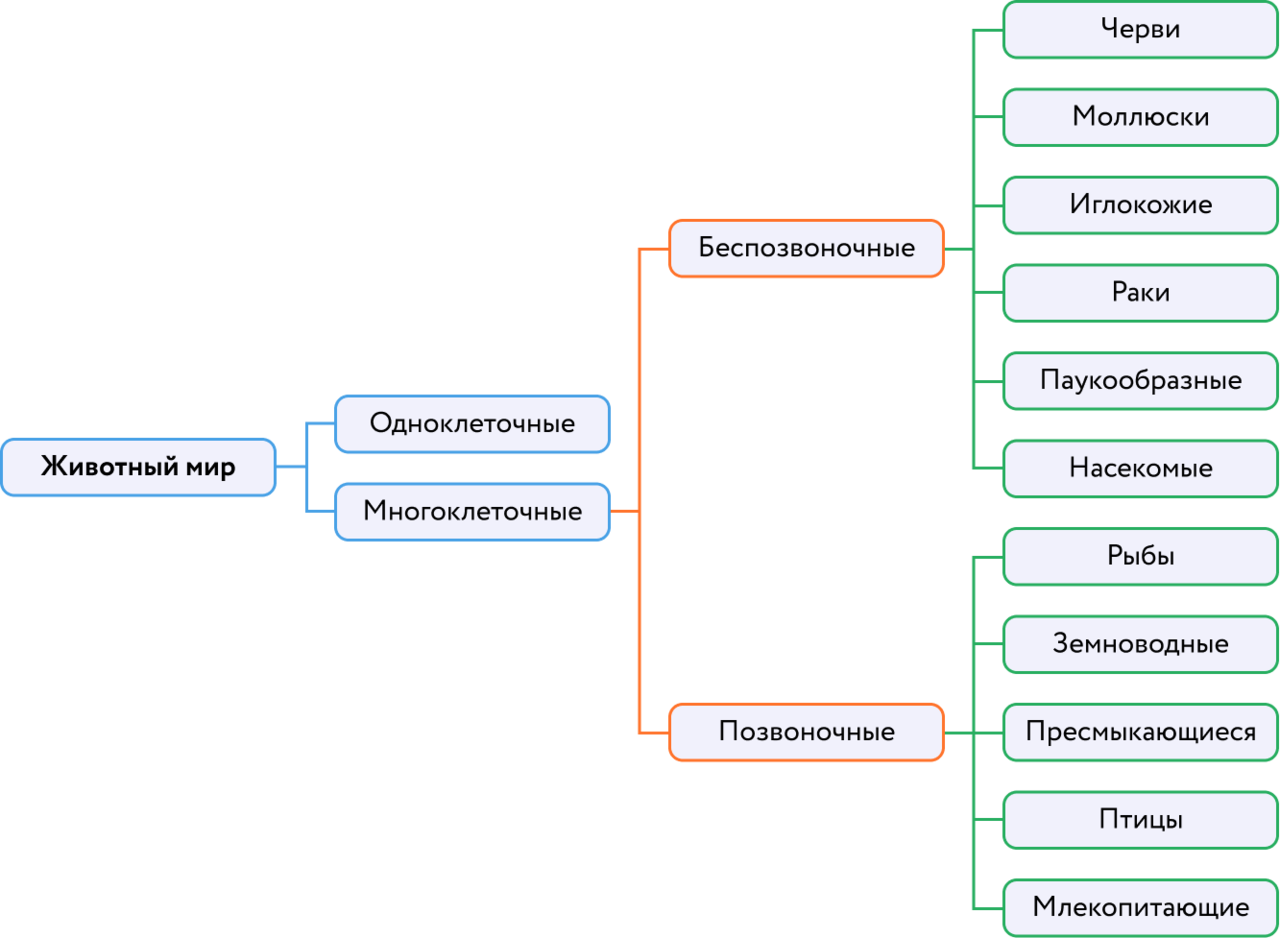
На уроках биологии вы уже работали с классификацией животного мира. В этом случае дерево могло быть ориентировано горизонтально. Такое расположение позволяет легко определить связи между отдельными элементами.

 В информатике чаще используется бинарное дерево. 

Бинарное дерево — дерево, каждый узел которого имеет не более двух потомков.

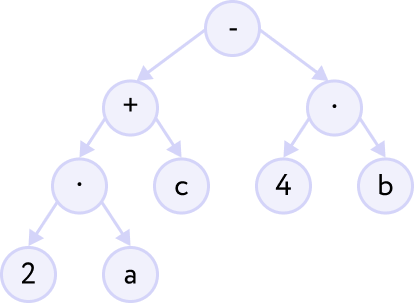
Бинарные деревья используют в информатике, чтобы определить значение арифметического выражения. Например, необходимо определить значение выражения: (2а + с) – 4b. Листья в этом случае — числа и переменные, а узлы — арифметические действия.

Д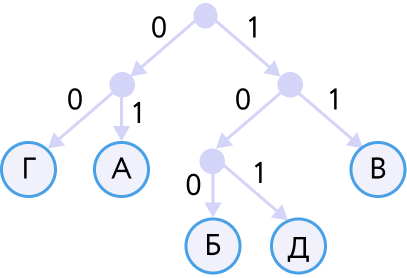 ля двоичных кодов тоже можно построить дерево. Например, построим дерево для кодирования следующих букв.

Дерево — очень удобная структура для представления информации, поэтому её используют во многих сферах.

5. Практическая работа

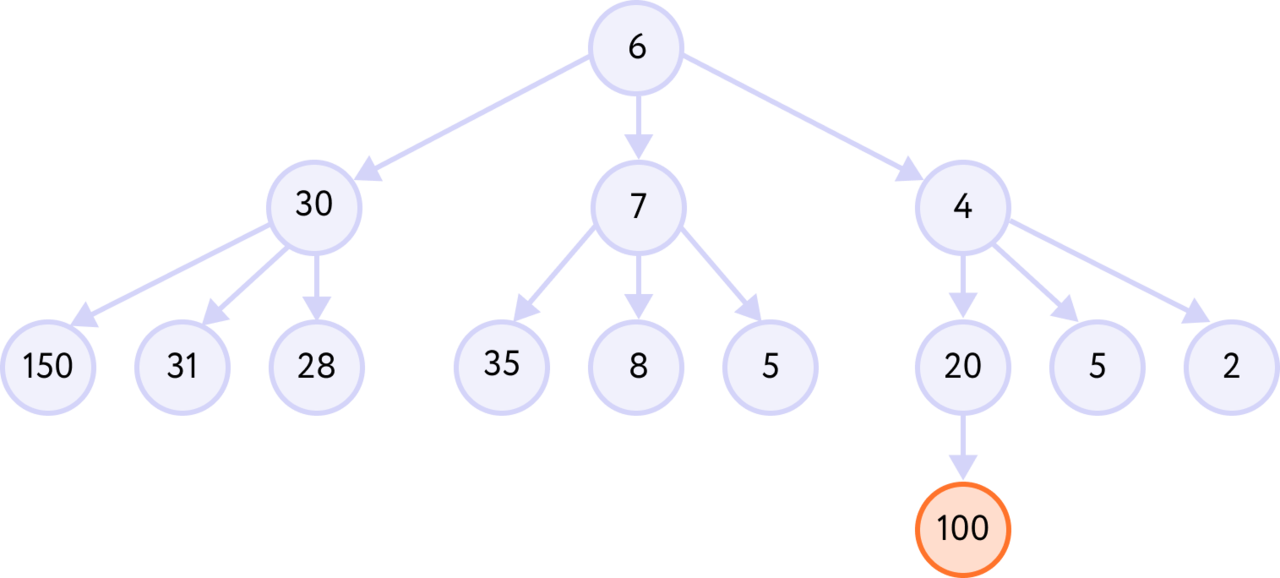
1. Перед вами таракашка с шестью ножками. Вам надо сделать из него стоножку, у которой ножек, естественно, 100. В вашем распоряжении три заклинания: УмножитьНа5, Прибавить1, Убрать2. Как выполнить превращение, использовав как можно меньше заклинаний?

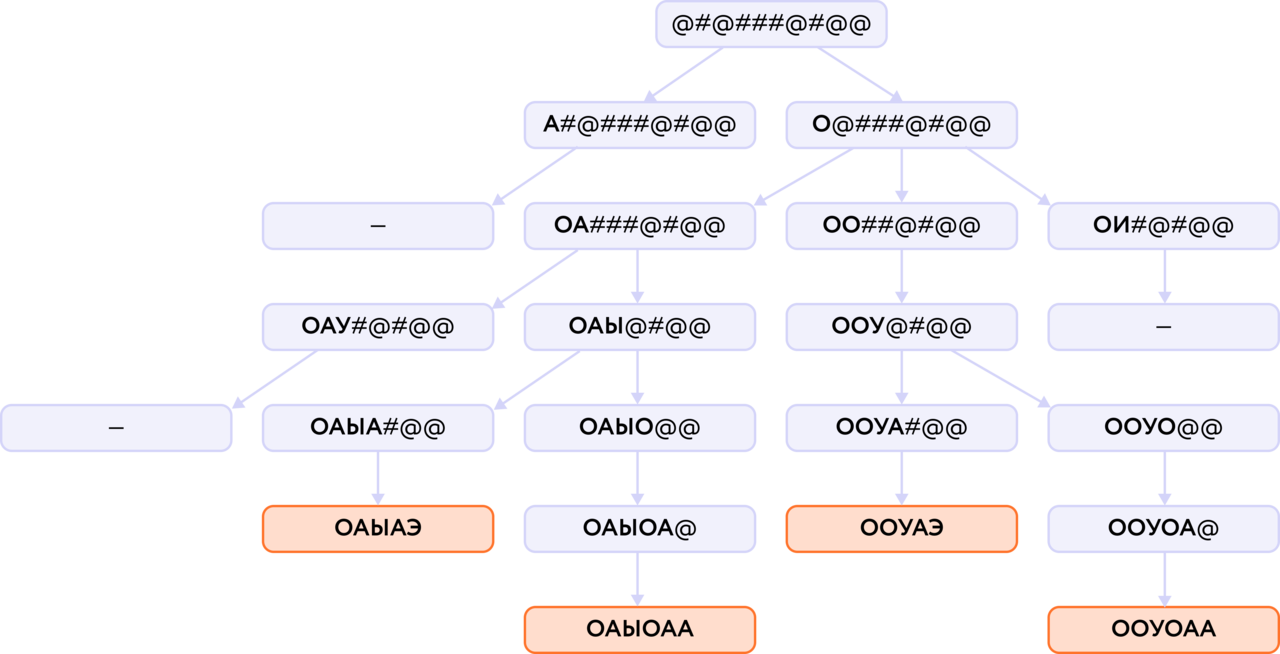
2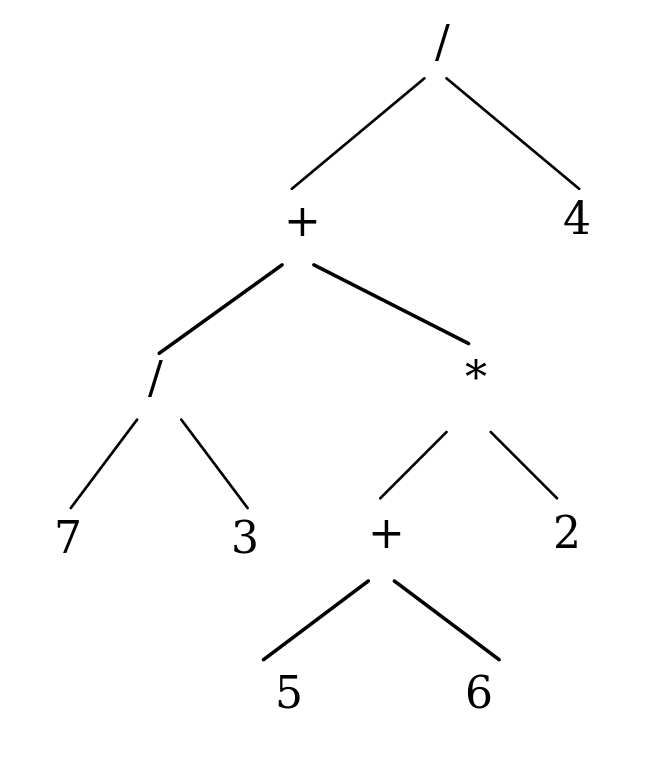 . Сколькими способами можно расшифровать сообщение @#@###@#@@, если известно, что А — это @, У — ##, О — @#, Э — #@@, И — @##, Ы — ###? Решите задачу с помощью дерева, на каждом уровне перебирая все варианты расшифровки очередной буквы.

3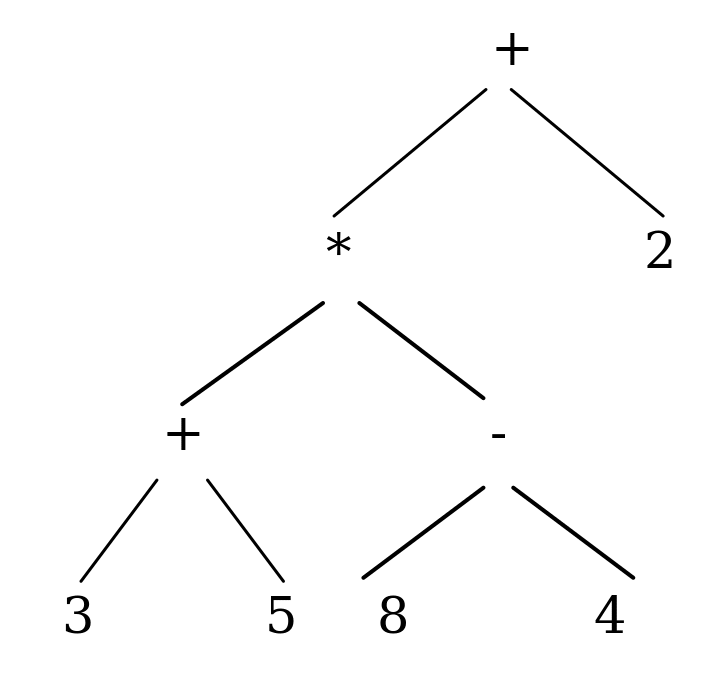 . (7/3+(5+6)*2)/4

4. (3+5)*(8-4)+2

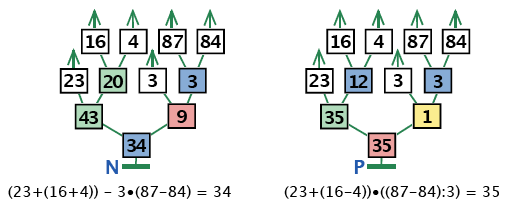
5.

6. Подведение итогов