ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕУЧРЕЖДЕНИЕ СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «КРАСНОКАМСКИЙ ЦЕЛЛЮЛОЗНО-БУМАЖНЫЙ ТЕХНИКУМ»
МЕТОДИЧЕСКАЯ РАЗРАБОТКА ПО ТЕМЕ: «ВЫЧИСЛЕНИЯ НА КАЛЬКУЛЯТОРЕ»
По дисциплине «Математика»
Выполнила: Филиппова М.А.
Рассмотрена и утверждена на заседании комиссии физико-математических дисциплин.
Протокол №_____ от «_____»______________20 г.
Г. Краснокамск.
2009-2010 учебный год
Пояснительная записка.
Изучение математики требует от студента большого объёма знаний. Технические средства обучения позволяют облегчить эту работу.
Данная методическая разработка предназначена для использования студентами дневной и заочной форм обучения на занятиях математики. В ней рассматривается теоретический материал по использованию калькуляторов разных типов, основные вопросы теории комплексных чисел. Кроме теоретических сведений изложены приёмы вычислений на калькуляторе различных алгебраических выражений и математических функций. Большой раздел занимает вычисление комплексных чисел с помощью калькулятора.
Данная работа так же может быть использована на занятиях специальных дисциплин, связанных с вычислительной работой, как студентами, так и преподавателями.
Введение.
Во все времена люди стараются облегчить вычислительную работу. Многие из вас помнят «Четырёхзначные таблицы Брадиса», логарифмическую линейку. Но всё это ушло в прошлое. А на смену пришли компьютеры и их младшие собратья – микрокалькуляторы (МК). Поэтому очень важным на уроках математики является умение грамотно, рационально использовать МК. Для этого необходимо знать принципы работы, назначение кнопок и многое другое. Для достижения необходимого результата ,начиная с первого курса, на уроках математики мы изучаем как правильно пользоваться различными МК. Эти знания студенты используют на старших курсах при решении расчётных задач, при выполнении курсовых и дипломных работ.
Как правильно работать на МК ребята начинают знакомиться на первом курсе при изучении той или иной темы. Например, при изучении темы «Степени» преподаватель объясняет, как правильно возводить в степень с действительным показателем на разных типах инженерных калькуляторах. При изучении темы «Погрешности» и «Округление чисел» разбирает, как округлять до нужного разряда и записывать число в стандартном виде, и т.д..
Типы калькуляторов:
Калькулятор является «инженерным», если на нём можно вычислять значения различных элементарных и трансцендентных функций, задавать элементарные программы.
Разберём два основных типа инженерных МК:
МК, у которых не высвечивается последовательность набора цифр и действий;
МК, у которых вычисляемое выражение полностью высвечивается на дисплее.
Вычисления на калькуляторах 1 типа.
1 тип МК:
Общие действии:
DRG
- устанавливает режим измерения углов – DEG - в градусах;
RAD – в радианах;
2ndF
GRAD – градиент (не используем).
- вторая функция – после нажатия, выполняется то, что написано над кнопкой.
 - стирание последних, не правильно набранных цифр.
- стирание последних, не правильно набранных цифр.
F-E
- запись числа в стандартном виде, например:
F-E
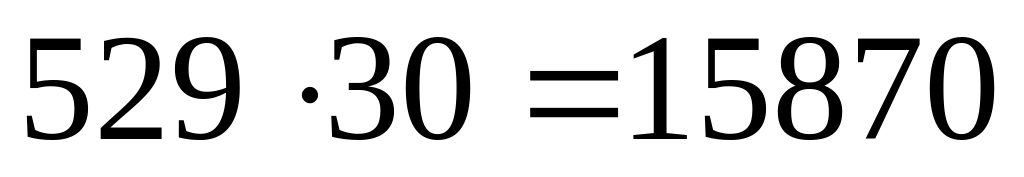

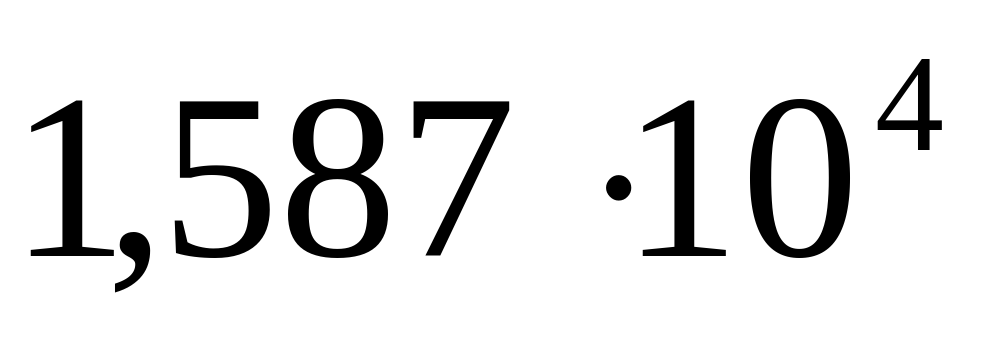 - F-E - (1,587 04) – пробел между числом и порядком числа оставлен для знака «минус».
- F-E - (1,587 04) – пробел между числом и порядком числа оставлен для знака «минус».
2ndF
F-E
Количество цифр после запятой
TAB
- - - округление числа до нужного разряда: 1 – до десятых; 2 – до сотых; 3 – до тысячных; и т.д.
0 – до единиц; точка – появляются все разряды.
(
)
- левая и правая скобки.
X-M
R-M
+/-
- смена знака числа.
Вычисление степеней:

Основание степени
YX
Показатель степени
=
- - -
Например:
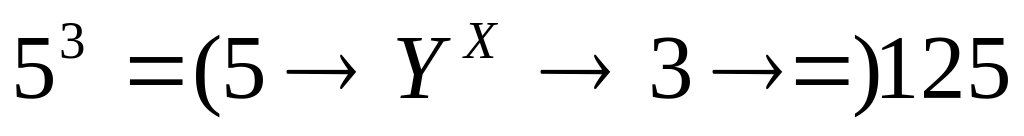
Вычисление корней:
Подкоренное выражение
2ndF
YX
Показатель корня
=
- - - -
Например:
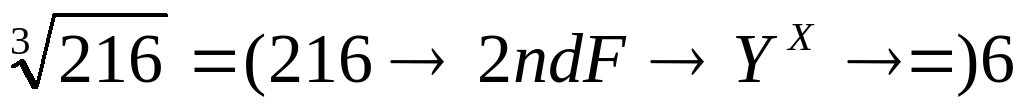
Вычисление логарифмов:
На МК имеются только десятичные и натуральные логарифмы. Для того, чтобы вычислять логарифмы с другими основаниями нужно воспользоваться формулой перехода от логарифма с одним основанием к логарифму с другим основанием:
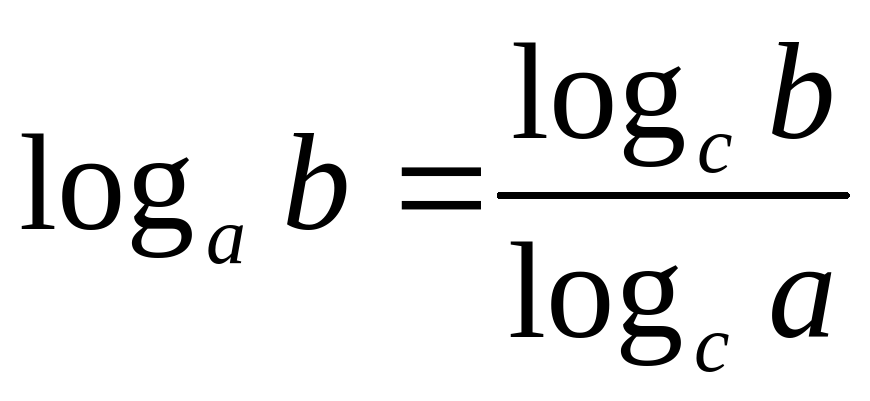
Число под логарифмом
Ln(или Lg)
Основание логарифма
Ln(или Lg)
=

- - - - - - -
Например:
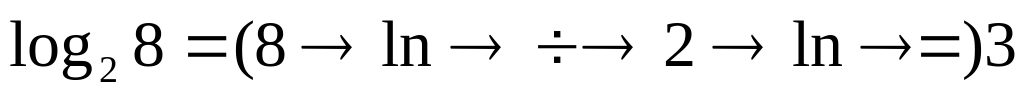
Вычисление тригонометрических функций:
Обычно при решении тригонометрических задач и при решении треугольников углы задаются в градусах, поэтому нужно установить режим МК – DEG.
Величина угла (град)
Тригонометрическая функция
-
Например:
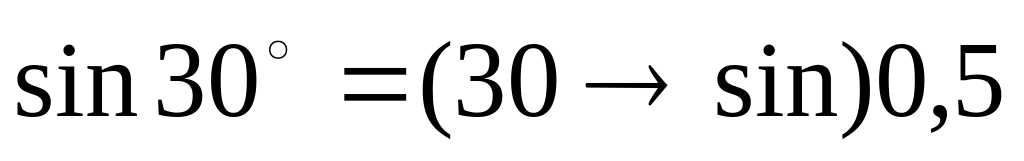
Аналогично вычисляются и другие тригонометрические функции.
Вычисление обратных тригонометрических функций:
Установить режим МК – DEG.
Значение тригонометрической функции
2ndF
Тригонометрическая функция
- -
Например:
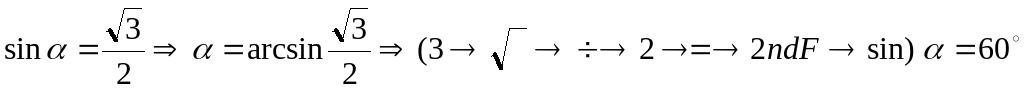
Аналогично вычисляются углы и с другими тригонометрическими функциями.
Вычисления на калькуляторах 2 типа.
Вычисления на МК 2 типа выполняются аналогично, но меняется последовательность набора.
Предлагаю вам несколько расчётных задач, которые решают студенты на занятиях.
Задача №1. Дисциплина «Процессы и аппараты»
В расчёте тепловых процессов при нагреве жидкостей, используют моделирование процессов через критериальные уравнения. Например: при определении коэффициента теплоотдачи от нагретой стенки к движущейся воде

Решение:
Задача2:Дисциплина «Основы экономики»
Найти процентную ставку по вкладу, если через10 лет 50000 рублей обратились в 1000000 рублей.
Р ешение:
ешение:
Вычисление комплексных чисел на МК.
Тема «Комплексные числа» является очень важной для специалистов «Электриков». Данная тема используется в дисциплине ТОЭ при расчёте цепей однофазного и трёхфазного переменного тока. А также в дисциплине «Электрические машины», где строятся векторные диаграммы на комплексной плоскости. Поэтому необходимо обучить студентов данной специальности грамотно и быстро выполнять расчёты, содержащие комплексные числа. А для этого очень важно научить студентов выполнять расчёты на инженерном калькуляторе.
Определение комплексного числа,
действия над комплексными числами в алгебраической форме
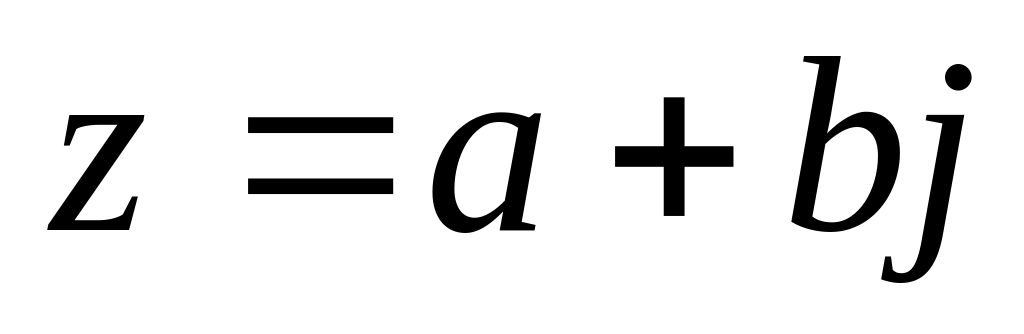 Комплексными числами называются числа вида ,
Комплексными числами называются числа вида ,
где 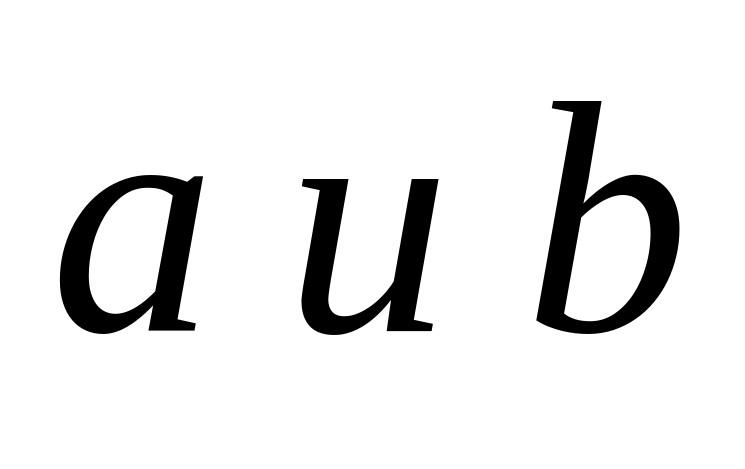 - действительные числа, а
- действительные числа, а 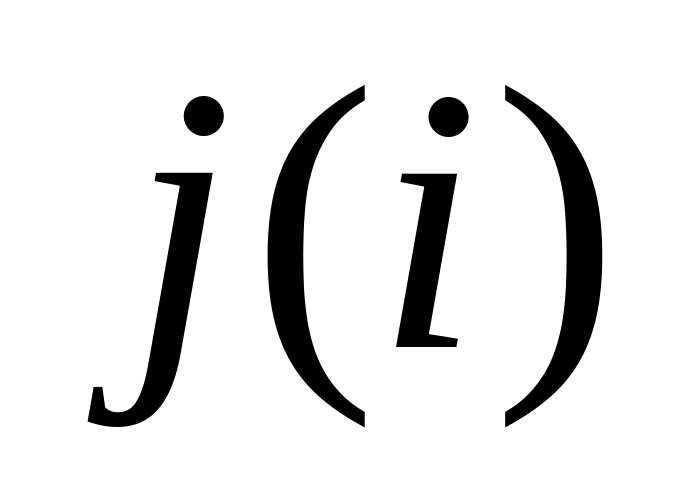 - мнимая единица (в электротехнике символ «i» заменили символом «j» т.к. «i» обозначает мгновенное значение силы тока).
- мнимая единица (в электротехнике символ «i» заменили символом «j» т.к. «i» обозначает мгновенное значение силы тока).
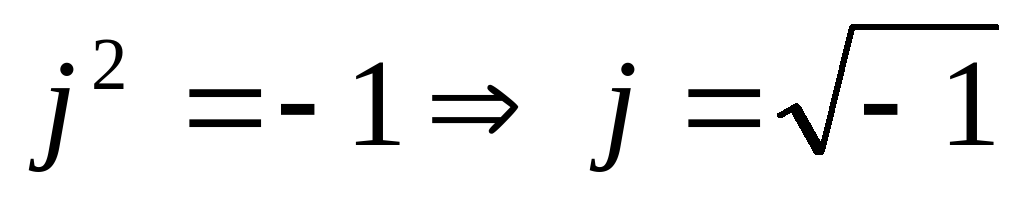
 -действительная часть комплексного числа;
-действительная часть комплексного числа;
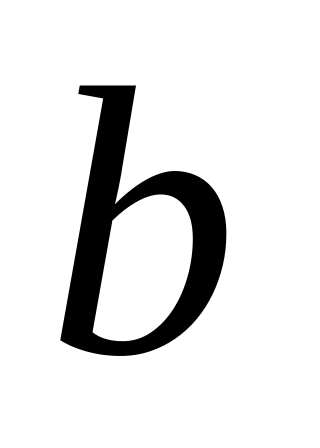 - мнимая часть комплексного числа.
- мнимая часть комплексного числа.
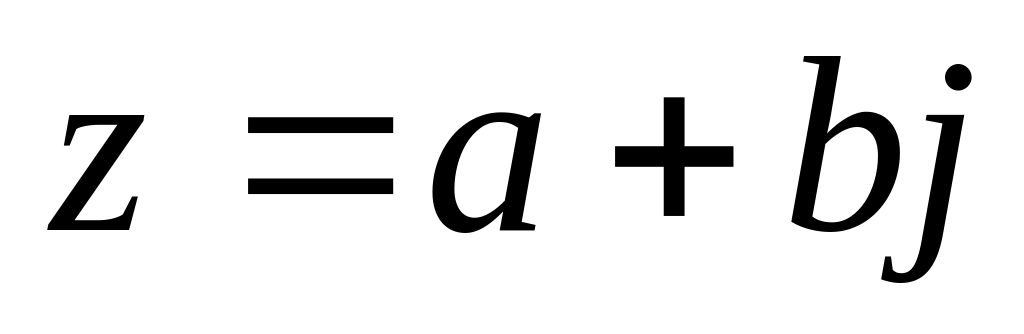
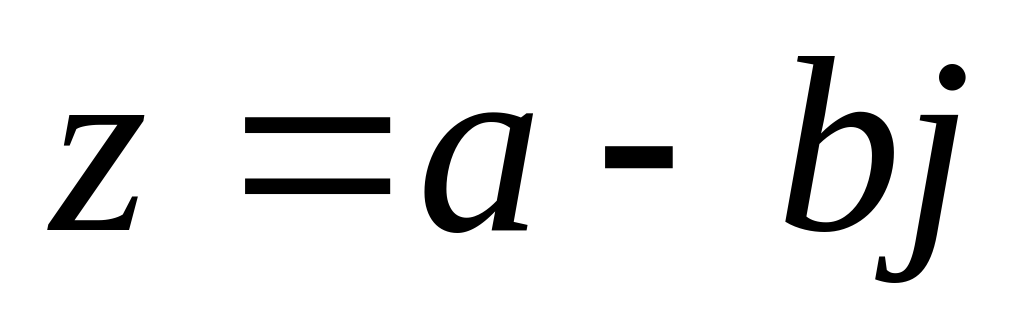 Числа и называются комплексно-сопряжёнными.
Числа и называются комплексно-сопряжёнными.
На множестве комплексных чисел выполняются все известные математические действия, в том числе и извлечение корня чётной степени из отрицательного числа.
Например:

При выполнении деления комплексных чисел нужно числитель и знаменатель умножать на число, сопряжённое знаменателю.
Геометрическое изображение комплексных чисел.
Модуль и аргумент комплексного числа.
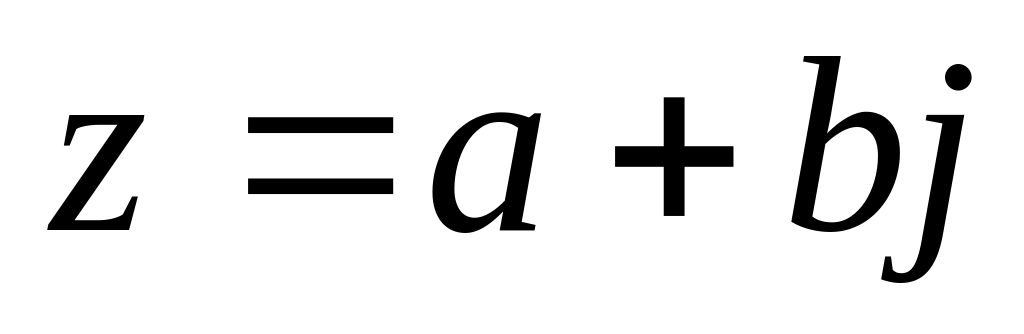
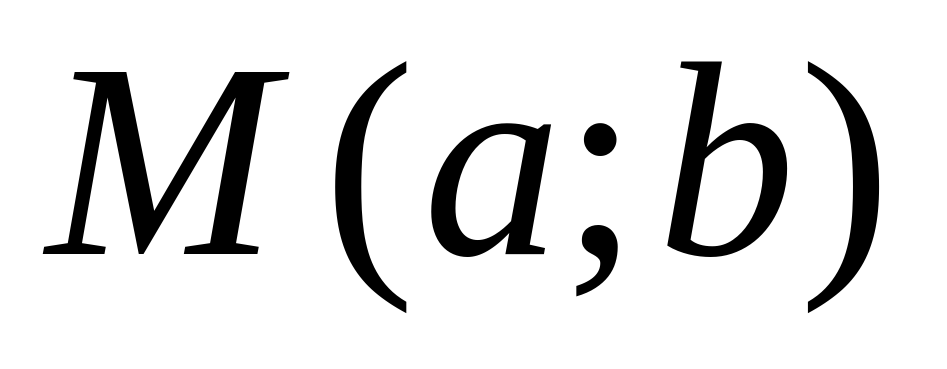
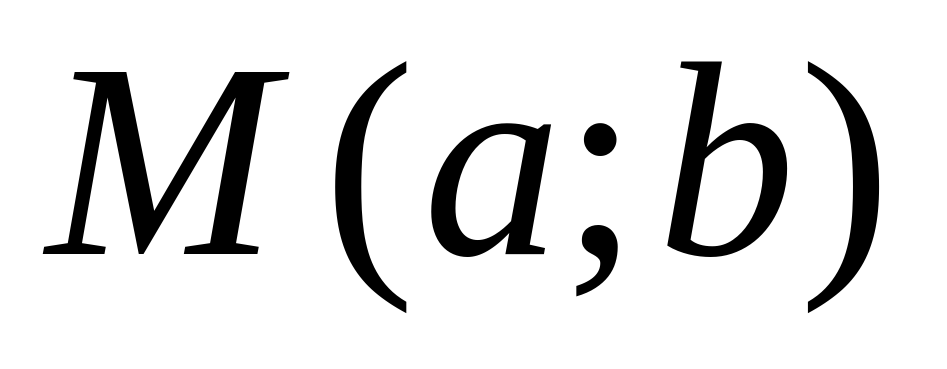 Любое комплексное число можно изобразить на координатной плоскости в виде точки , где по оси Ох отмечают действительную, а по оси Оу мнимую часть комплексного числа. Каждой точке плоскости с координатами соответствует один и только один вектор с началом в точке и концом в точке . Он называется радиус – вектором. Длина этого вектора называется модулем комплексного числа и вычисляется по формуле , а угол, образованный радиус-вектором с положительным направлением оси Ох , называется аргументом комплексного числа. Радиус вектор вычисляется по формуле: (учитывая четверть). Аргумент определяется неоднозначно. Наименьшее по абсолютной величине значение аргумента из промежутка называется главным значением аргумента.
Любое комплексное число можно изобразить на координатной плоскости в виде точки , где по оси Ох отмечают действительную, а по оси Оу мнимую часть комплексного числа. Каждой точке плоскости с координатами соответствует один и только один вектор с началом в точке и концом в точке . Он называется радиус – вектором. Длина этого вектора называется модулем комплексного числа и вычисляется по формуле , а угол, образованный радиус-вектором с положительным направлением оси Ох , называется аргументом комплексного числа. Радиус вектор вычисляется по формуле: (учитывая четверть). Аргумент определяется неоднозначно. Наименьшее по абсолютной величине значение аргумента из промежутка называется главным значением аргумента.
2
2
Пример: Найти модуль и аргумент комплексного числа .
Решение:
Тригонометрическая и показательная формы
к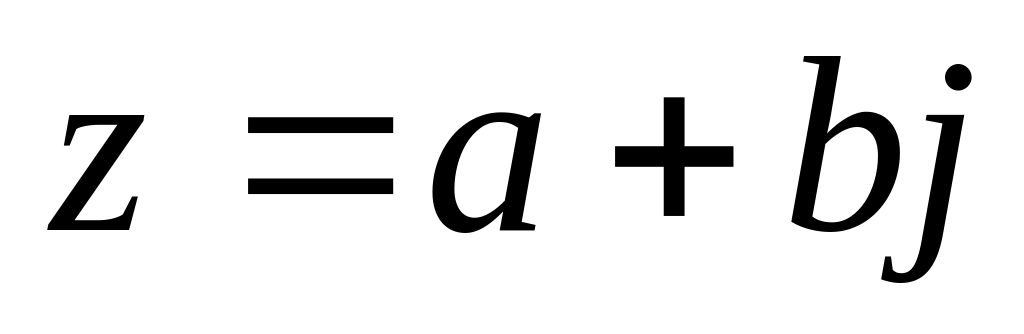 омплексного числа.
омплексного числа.
Кроме алгебраической формы существует ещё две формы: тригонометрическая и показательная.
В алгебраической форме удобно выполнять действия сложения и вычитания, а в показательной и тригонометрической формах удобно выполнять умножение, деление, возведение в степень и извлечение корня.
Выполните действия:
Найдите модуль и аргумент комплексного числа .
Решение:
Проверка заданий:
____________________________________________________________________
Как видите, вычисления комплексных чисел вызывают определённые затруднения. Особенно действия умножения, деления, нахождение модуля и аргумента комплексного числа. А если учесть, что задания с комплексными числами являются частью других задач по электротехнике или по электрическим машинам, то естественно хочется найти способ, позволяющий ускорить и облегчить эту работу. Таким помощником для нас является калькулятор. В начале первого курса мы просим всех студентов приобрести инженерные калькуляторы. Для специальности «Электрик» калькуляторы должны содержать кнопочки:
r
 e ху cpl x
e ху cpl x
a
b

а) Выполнение арифметических действий над комплексными числами.

«действительная часть числа - кнопка - мнимая часть числа - кнопка
- мнимая часть числа - кнопка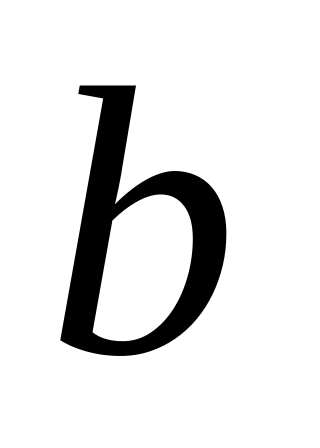 »;
»;
Нажать знак «=», после чего появится действительная часть результата;
Нажать кнопку «b»,после чего появится мнимая часть результата.
Пример:
Решение:
В режиме комплексных чисел выполнить действия:
12 –«a» - 9 – «b» - «:» - 4 – «+/-» - «a» - 2 – «+/-» - «b»-
- «=» (получим действительную часть результата «-3.3») - «b»(получим мнимую часть результата «-0.6»)
Можно проверить с помощью калькулятора предыдущие примеры.
б) Нахождение модуля и аргумента комплексного числа.
Установить с помощью кнопки «DRG» режим калькулятора «DEG» (т.е. величина угла будет показана в градусах; если нужно величину угла в радианах, то с помощью этой же кнопки установить режим «RAD»);
Набрать комплексное число на калькуляторе:
«действительная часть числа - кнопка - мнимая часть числа - кнопка
- мнимая часть числа - кнопка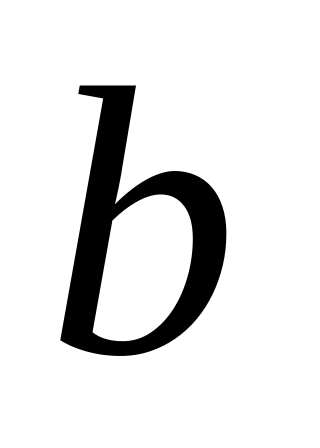 »;
»;
Пример:
Перевести число z= 5+10j в показательную и тригонометрическую формы.
Решение:
Найдём модуль и аргумент данного комплексного числа:
5-«a» - 10 – «b» - «2ndF» - «a» (получим модуль данного числа 11,18 ) – «b» - -(получим аргумент данного числа 63,430 ).
Z=11,18(cos 63,430+jsin63,430) – тригонометрическая форма);
Z=11,18 ej63,46- показательная форма.
В качестве закрепления нового материала можно решить задачи из сборника по ТОЭ.
12






 - стирание последних, не правильно набранных цифр.
- стирание последних, не правильно набранных цифр.
 ешение:
ешение:










