ПРАКТИЧЕСКАЯ РАБОТА №2
Учебная дисциплина: Математика: начала математического анализа; геометрия
Тема: Вычисление производной функции.
Цель занятия: Закрепить и обобщить знания о формулах и правилах нахождения производных; совершенствовать умения и навыки нахождения производных.
Методические рекомендации.
Опр. Производной функции f(x) в точке х называется предел разностного отношения 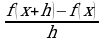 при
при 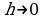 .
. 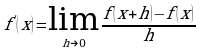 .
.
Опр. Операция нахождение производной называется дифференцированием.
Это правило является основным, т.к. выведено из самого определения. Однако при дифференцировании сложных функций, суммы, произведения, частного применение общего правила представляет большие трудности. Поэтому применяют правила дифференцирования.
Правила
1. 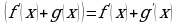 - Производная суммы равна сумме производных.
- Производная суммы равна сумме производных.
2. 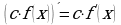 - Постоянный множитель можно вынести за знак производной.
- Постоянный множитель можно вынести за знак производной.
3. 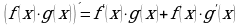 - Производная произведения.
- Производная произведения.
4. 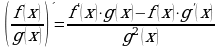 Производная частного
Производная частного
Формулы дифференцирования
С′ = 0 11. 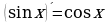
( х ) ′ = 1 12. 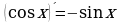
( х 2 ) ′ = 2х 13. 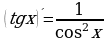
( х 3) ′ = 3х2
( х р ) ′ = р х р – 1 14. 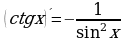
( е х ) ′ = е х 15.
15. 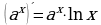
7. 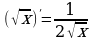 16.
16. 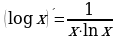
8. 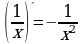 17.
17. 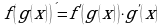
9. 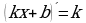 18.
18. 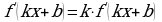
10. 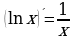
При решении задач на нахождение уравнения касательной к графику функции в точке используется геометрический смысл производной 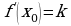
Уравнение касательной 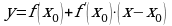
Пример 1. Найти производную функции f(x) = 9.
Решение: f ' (x) = 9' = 0.
Пример 2. Найти производную функции f(x) = x.
Решение: f ' (x) = x' =1
Пример 3. Найти производную функции f(x) = х2.
Решение: f ' (x) = (х2)' = 2х2-1 = 2х1 = 2х.
Пример 4. Найти производную функции f(x) = 7х3.
Решение: f ' (x) = (7х3)' = 7·3х3-1 = 21х2.
Пример 5. Найти производную функции f(x) = х-5.
Решение: f ' (x)=(х-5)' =-5х-5-1 = -5х-6 = - 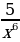 .
.
Пример 6. Найти производную функции f(x)=х6+х3-4.
Решение: f ' (x) =(х6)'+(х3)' - 4'=6х6-1 +3х3-1 – 0=6х5 +3х2.
Пример 7. Написать уравнение касательной к графику функции у = f(x) в точке с абсциссой х0 , если f(x) = х - 3х2, х0 = 2.
Решение: у = f(x0)+f '(x0) · (x-x0).
1. f(x0)= f(2)=x0 -3x0 2=2-3·22 =2- 3·4 = 2-12=10.
2. f '(x0)= (x0 -3x0 2)'=(x0)' – (3x0 2)'=1-3·2x0 2-1=1- 6 x0=1-6·2=1-12=11.
3. у = f(x0)+f '(x0) · (x-x0) = 10 +11· (x - 2).
Ответ: y= 10 +11· (x - 2).
Самостоятельная работа
Пример 1. Найти производную функции f(x) = 8.
Пример 2. Найти производную функции f(x) = x.
Пример 3. Найти производную функции f(x) = х7.
Пример 4. Найти производную функции f(x) = 4х3.
Пример 5. Найти производную функции f(x) = х-9.
Пример 6. Найти производную функции f(x) = х5+х3 – 10.
Пример 7. Написать уравнение касательной к графику функции у = f(x) в точке с абсциссой х0 , если f(x) = х - 6х2 , х0 = 1.





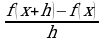 при
при 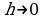 .
. 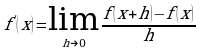 .
. 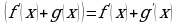 - Производная суммы равна сумме производных.
- Производная суммы равна сумме производных.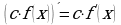 - Постоянный множитель можно вынести за знак производной.
- Постоянный множитель можно вынести за знак производной.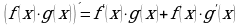 - Производная произведения.
- Производная произведения.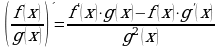 Производная частного
Производная частного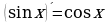
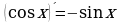
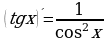
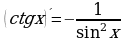
 15.
15. 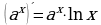
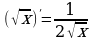 16.
16. 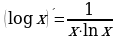
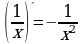 17.
17. 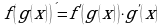
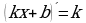 18.
18. 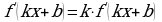
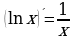
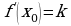
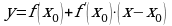
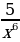 .
.









