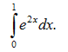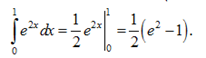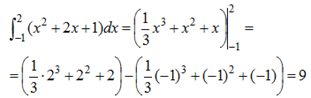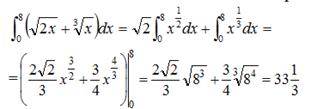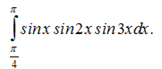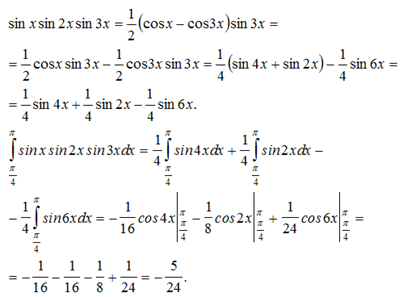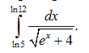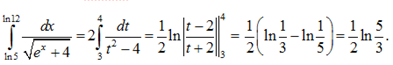Лекция №15
Тема: Вычисление определенного интеграла.
План.
Определение определенного интеграла.
Геометрический смысл определенного интеграла
Примеры определенного интеграла.
Определенный интеграл – Это число, значение которого вычисляется по формуле Ньютона - Лейбница:
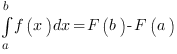
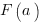 - это значение первообразной функции
- это значение первообразной функции 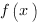 в точке
в точке 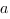 , и, соответственно,
, и, соответственно, 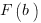 - это значение первообразной функции
- это значение первообразной функции 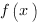 в точке
в точке 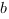 .
.
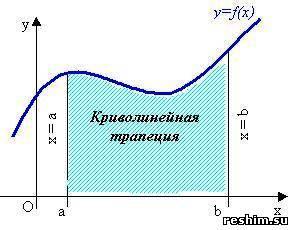
Геометрический смысл определенного интеграла:
Определенный интеграл 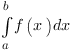 - это число, равное площади криволинейной трапеции - фигуры, ограниченной сверху графиком положительной на отрезке
- это число, равное площади криволинейной трапеции - фигуры, ограниченной сверху графиком положительной на отрезке 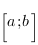 функции
функции 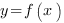 , слева прямой
, слева прямой 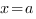 , справа прямой
, справа прямой 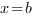 , и снизу осью ОХ.
, и снизу осью ОХ.
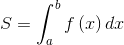
Если функция y = f(x) неположительная на отрезке [a; b], то площадь криволинейной трапеции может быть найдена как 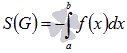 .
.
Пример 1. Вычислить интеграл
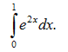
Решение.
На основании таблицы основных интегралов и формулы (1) имеем:
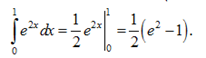
Пример 2. Вычислить интеграл
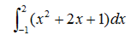
Решение.
На основании таблицы основных интегралов и формулы (1) имеем:
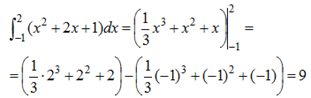
Пример 3. Вычислить интеграл
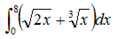
Решение.
На основании таблицы основных интегралов и формулы (1) имеем:
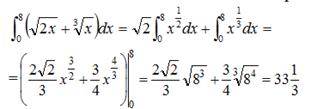
Пример 4 Вычислить интеграл
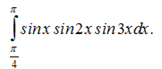
Решение.
На основании формулы произведения синусов, таблицы основных интегралов и формулы (1) имеем:
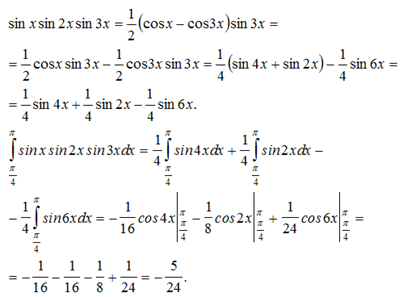
Пример 5. Вычислить интеграл
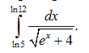
Решение.
На основании таблицы основных интегралов и формулы (2) имеем:
Сделаем замену ex + 4 = t2, тогда ex= t2– 4, ex dx = 2t dt,
Если x= ln5, то t = 3; если x= ln12, то t = 4. Тогда
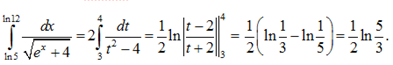
Пример 6. Вычислить интеграл
Решение.
На основании таблицы основных интегралов и формулы (2) имеем:
Пример 7. Вычислить интеграл
Решение.
На основании таблицы основных интегралов и формулы (2) имеем:
Сделаем подстановку t = cosx
Если x = 0, то t = cos 0 = 1, если
Следовательно
Пример 8. Вычислить интеграл
Решение.
На основании таблицы основных интегралов и формулы (2) имеем:
Найдем пределы по t:
Находим
Следовательно,
Пример 9. Вычислить интеграл
Решение.
Хороший метод решения интегралов, это метод занесения под дифференциал, его плюс состоит в том, что не требуется менять пределы интегрирования
Пример 10. Вычислить интеграл
Решение. На основании таблицы основных интегралов и формулы (3) имеем (интегрируем по частям)
Самостоятельная работа по теме «Интеграл»
| Уровень | 1 - Вариант | 2 - Вариант |
| 1 - 2 | 1. Что такое интеграл ? 2. Верно ли, что 
| 1. Напишите формулу Ньютона – Лейбница. 2. Верно ли, что 
|
|
3 - 6 | Вычислите интегралы
| Вычислите интегралы
|
|
7 - 10 | Вычислите интегралы


| Вычислите интегралы 

|
Условия оценки
Выполнение заданий каждого уровня оценивается соответствующей оценкой.
Можно выполнять задания из разных уровней. При этом будет учитываться сложность примеров и количество верно решённых заданий.
Оценка повышается в случае выполнения заданий более высокого уровня.







 - это значение первообразной функции
- это значение первообразной функции  в точке
в точке  , и, соответственно,
, и, соответственно,  - это значение первообразной функции
- это значение первообразной функции  .
.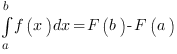
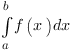 - это число, равное площади криволинейной трапеции - фигуры, ограниченной сверху графиком положительной на отрезке
- это число, равное площади криволинейной трапеции - фигуры, ограниченной сверху графиком положительной на отрезке 
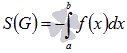 .
.