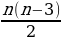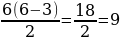Выпуклый многоугольник.

Тема урока: Выпуклый многоугольник

Тип урока: Урок изучения нового материала

Продолжительность: 45 мин

Цель урока: Формирование представления о выпуклых многоугольниках, овладение навыком распознавания и построения выпуклых фигур, формирование умения различать свойства выпуклых и невыпуклых многоугольников.

Ход урока:

I. Организационный этап (2 минуты)

— Здравствуйте, уважаемые ребята! Начинаем наш сегодняшний урок геометрии. Думаю, он станет интересным и полезным для каждого из вас.

Обращаюсь лично к некоторым ученикам:

— Наташа, готова к уроку? Денис, вижу твою улыбку, надеюсь, настроение хорошее? Павел, приготовил тетрадь и ручку?

И далее обращаю внимание всех:

— Наш урок посвящён одной интересной теме — выпуклым многоугольникам. Она кажется сложной, но уверяю вас, мы обязательно поймём её суть и научимся отличать выпуклые фигуры от невыпуклых. Надеюсь, к концу урока вы сможете уверенно оперировать этими понятиями и строить собственные красивые геометрические конструкции.

— Приступим!

II. Повторение изученного материала (5 минут)

Прежде чем перейти к новому материалу, давайте быстро освежим в памяти базовые понятия, которые понадобятся нам сегодня.

Вопрос первый:

— Расскажите, что такое многоугольник вообще? Приведите пример.(Предполагаемый ответ: Многоугольник — это замкнутая плоская фигура, образованная несколькими прямыми линиями.)

Следующий вопрос:

— Сколько углов у правильного четырёхугольника? А у правильного пятиугольника? (Вероятно последует ответ: Четырёхугольник имеет четыре угла, пятиугольник — пять.)

Третий вопрос:

— Какие типы многоугольников вам знакомы? Перечислите хотя бы три.(Возможные варианты: треугольники, квадраты, ромбы, трапеции, параллелограммы.)

Молодцы, отлично вспомнили необходимые вещи! Теперь будем двигаться дальше, и изучать новое важное свойство — выпуклость многоугольников.

III. Объяснение нового материала (15 минут)

1. Определение выпуклого многоугольника

— Переходим к основной части нашего урока. Сегодня мы узнаем, что такое выпуклый многоугольник. Важно понимать, что не всякий многоугольник обладает таким свойством, и знание особенностей выпуклых фигур пригодится нам впоследствии.

Определение: Запишите в тетради:

Выпуклый многоугольник — это такой многоугольник, у которого любая прямая, проходящая через любую внутреннюю точку, пересекает границу многоугольника ровно в двух точках.

Или иначе: Выпуклый многоугольник — это фигура, в которой прямой отрезок, соединяющий любые две внутренние точки, целиком лежит внутри фигуры.

Переводим это на русский язык простыми словами: представьте себе фигуру, внутри которой мы проводим прямую линию между любыми двумя точками. Если вся эта линия остаётся внутри фигуры — значит, она выпуклая.

Для примера: нарисуем обычный треугольник и прямоугольник — обе фигуры выпуклые. Попробуйте провести отрезок внутри них — увидите, что он всегда останется внутри.

Но если нарисовать звезду, криволинейную фигуру или многоугольник с углублениями, легко заметить, что отрезок выходит наружу — значит, это не выпуклый многоугольник.

Есть ещё одно простое свойство выпуклых многоугольников: все внутренние углы выпуклого многоугольника меньше 180∘.

Таким образом, запоминаем основное:— Выпуклый многоугольник — это тот, у которого отрезок между любыми внутренними точками не выходит за границы.— Внутренние углы таких фигур всегда острые или прямые (∘).

2. Примеры и контрпримеры

— Сейчас приведу несколько ярких примеров и контрпримеров, чтобы окончательно зафиксировать ваше представление о выпуклых и невыпуклых многоугольниках.

Примеры выпуклых многоугольников:

• Треугольник: Всегда выпуклый, так как ни одна сторона не выходит внутрь фигуры.

• Прямоугольник: Углы по 90∘90∘, все стороны параллельны противоположным сторонам — следовательно, всегда выпуклый.

• Квадрат: Равенство всех сторон и углов делает его идеальным примером выпуклой фигуры.

• Регулярный пятиугольник: Все стороны одинаковой длины, все углы одинаковые — идеальный выпуклый многоугольник.

Контрпримеры (невыпуклые многоугольники):

• Звезда Давида: Имеет внутренние впадины, значит, это неверный выпуклый многоугольник.

• Самопересекающийся многоугольник: Когда стороны пересекаются друг с другом, фигура автоматически превращается в невыпуклую.

• Многоугольник с острым углом снаружи: Представьте шестиугольник, у которого один угол значительно выдвинут вперёд, создавая внешний острый угол — он также будет считаться невыпуклым.

Попытайтесь представить подобные формы мысленно или изобразить их на листочке бумаги. Это облегчит понимание.

Главное помнить:

• Все стороны и углы лежат внутри фигуры — признак выпуклости.

• Наличие "углублений" или острых выступающих частей — признаки невыпуклости.

3. Число диагоналей выпуклого n-угольника

— Теперь пришло время познакомиться с важным математическим фактом, связанным с количеством диагоналей в любом выпуклом многоугольнике. Эта формула полезна не только для решения задач, но и для глубокого понимания структуры самих фигур.

Вот оно, запомните:

Количество диагоналей выпуклого n-угольника =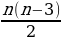

Расшифрую формулу пошагово:

• n— это количество сторон (вершин) многоугольника.

• Умножаем это число на (n−3), потому что каждые две соседние вершины образуют сторону, а не диагональ.

• Полученную величину делим пополам, так как каждая диагональ учитывалась дважды (ведь можно идти от первой вершины ко второй и наоборот).

Покажу применение формулы на простом примере:

Допустим, у нас есть шестиугольник (n=6), считаем количество диагоналей:

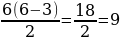
То есть у шестигранника девять диагоналей. Попробуем применить формулу и для других случаев.

Сумма внутренних углов многоугольника:

S=(n−2)⋅180∘

Эта формула позволяет рассчитать общую меру углов, зная количество сторон. Оба этих инструмента важны для полного понимания свойств выпуклых многоугольников.

IV. Первичное закрепление (10 минут)

— Сейчас попробуем закрепить изученный материал на практике. Возьмите карандаши и ручки, откройте чистые страницы ваших тетрадей.

Первое задание: Нарисуйте треугольник, четырехугольник и пятиугольник. Проверьте, соответствуют ли они определению выпуклого многоугольника. Обязательно проведите отрезки между разными вершинами и убедитесь, что они действительно остаются внутри фигуры.

Второе задание: По предложенной нами формуле рассчитайте количество диагоналей у семиугольника и девятиугольника. Кто справится быстрее, пусть поднимет руку, и мы вместе проверим правильность решений.

Напоминаю: чтобы точно построить правильную диаграмму, следите за пропорциями сторон и измеряйте углы.

Если возникают вопросы, обращайтесь ко мне за советом. Работа индивидуальная, можете обсудить ваши мысли с товарищами рядом, но отвечать будете самостоятельно.

Время пошло, желаю удачи!

V. Физкультминутка (2 минуты)

✅ Упражнение для снятия усталости глаз:— Быстро моргаем глазами 10 секунд.— Затем смотрим вдаль, стараясь расслабиться.

✅ Растяжка плеч и шейного отдела позвоночника:— Медленно поворачиваем голову вправо-влево, затем вверх-вниз.— Круговые вращения плечами вперед и назад.

✅ Простые наклоны туловища:— Сидя прямо, наклоняемся вперед, пытаясь достать руками пол.— Возвращаемся обратно и расслабляемся.

✅ Легкая гимнастика для кистей рук:— Крепко сжимаем пальцы в кулак и резко распрямляем кисти.— Кладём ладони на стол и слегка массируем их круговыми движениями.

🌟 После завершения движений возвращаемся к рабочему ритму спокойным вдохом-выдохом.

VI. Самостоятельная работа (10 минут)

Решение индивидуальных карточек-заданий разного уровня сложности. Возможна помощь учителя.

Примеры заданий:

1. Доказать, что правильный шестиугольник — выпуклая фигура.

2. Найти общее количество диагоналей в восьмиугольнике.

VII. Рефлексия (3 минуты)

— Настало время оценить, насколько продуктивно прошёл наш урок. Ответьте честно самим себе и своим одноклассникам:

1. Поняли ли вы, что такое выпуклый многоугольник?

2. Освоили ли вы формулу для расчёта количества диагоналей?

3. Есть ли трудности или непонятные моменты?

Те, кому было сложно, расскажите, что вызвало затруднения. Вместе сможем преодолеть препятствия.

Если остались вопросы, прошу подойти после урока — обсудим дополнительно.

Спасибо за хорошую работу, сегодня вы проявили отличную активность и желание учиться. Пусть следующий урок принесёт вам радость открытий и успеха в изучении геометрии!

VIII. Домашнее задание (3 минуты)

Домашняя работа:

• Глава 6,§46 упражнения №464, №465