Взаимное расположение прямых в пространстве

Взаимное расположение прямых

в пространстве

D

A

C

B

Математический диктант

Критерии оценки:

10-11- «5»

7-9- «4»

5-6- «3»

1. Запишите с помощью символов

• Прямые d и с пересекаются в точке В.
• Точка А лежит в плоскости α, но не лежит на прямой а.
• Плоскости α и β пересекаются по прямой с.
• Точки А, В лежат в плоскости α, точка M не лежит в плоскости α.

2. Изобразите

• 1) Две пересекающиеся плоскости.
• 2) Прямую, пересекающую плоскость.
• 3) Плоскость, проходящую через две пересекающиеся прямые.

3. Ответьте на вопросы

• 1) Сколько плоскостей можно провести через одну точку?
• 2) Сколько плоскостей можно провести через две точки?
• 3) Сколько плоскостей можно провести через три точки, не лежащие на одной прямой?
• 4) Сколько плоскостей можно провести через одну прямую?





Параллельные прямые в пространстве

Каково может быть взаимное расположение двух прямых на плоскости?

1

(совпадают, пересекаются, параллельны)

Дайте определение параллельных прямых на плоскости.

2

Параллельными называются прямые, лежащие в одной плоскости и не пересекающие друг друга.

)

(

a

 ,



b

a

b

a ∩

b

© Кузьмина Е.А., Колобовская МСОШ, 2010





Параллельные прямые в пространстве

Параллельными прямыми в пространстве называются прямые, лежащие в одной плоскости и не пересекающие друг друга.

(

)

a

 ,



b

a

b

a ∩

b

© Кузьмина Е.А., Колобовская МСОШ, 2010





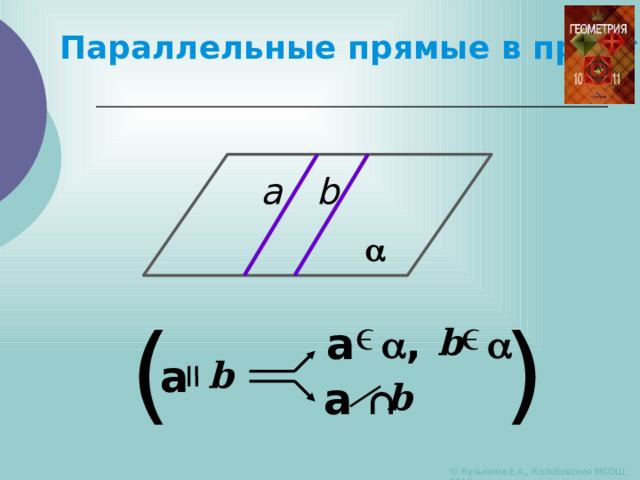
Параллельные прямые в пространстве

a b



)

(

a

 ,



b

a

b

a ∩

b

© Кузьмина Е.А., Колобовская МСОШ, 2010

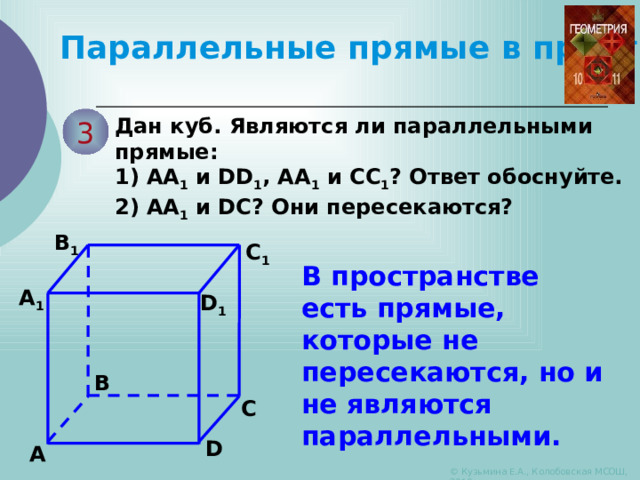
Параллельные прямые в пространстве

Дан куб. Являются ли параллельными прямые:

3

1) АА 1 и DD 1 , АА 1 и СС 1 ? Ответ обоснуйте.

2) АА 1 и DС? Они пересекаются?

B 1

C 1

В пространстве есть прямые, которые не пересекаются, но и не являются параллельными.

A 1

D 1

B

C

D

A

© Кузьмина Е.А., Колобовская МСОШ, 2010

Параллельные прямые в пространстве

Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

c b

© Кузьмина Е.А., Колобовская МСОШ, 2010



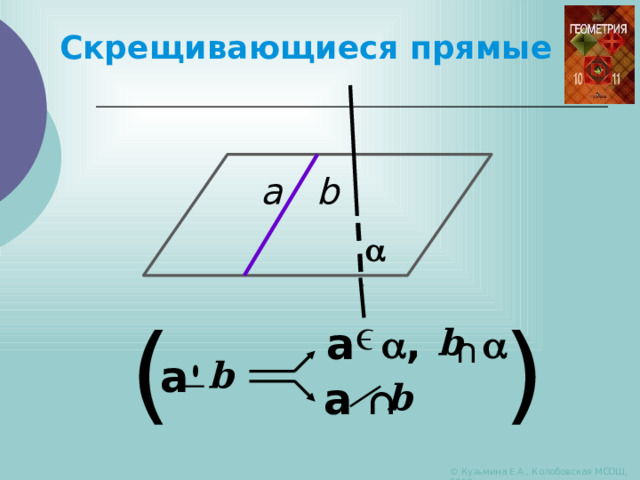
Скрещивающиеся прямые

a b



)

(

a

⋂ 

b

 ,

a

b

a ∩

b

© Кузьмина Е.А., Колобовская МСОШ, 2010

Параллельные прямые в пространстве

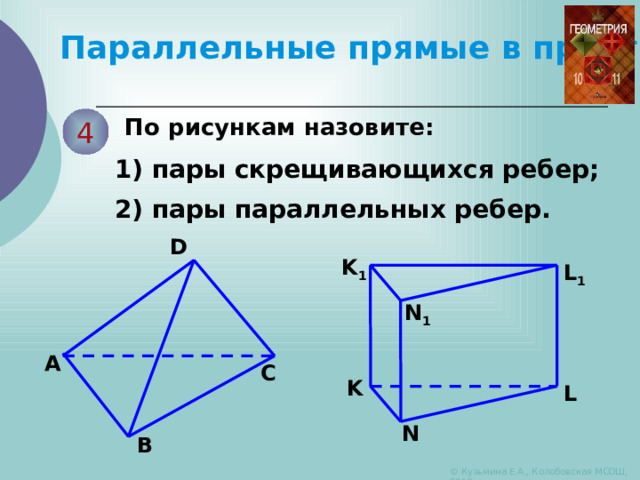
По рисункам назовите:

4

1) пары скрещивающихся ребер;

2) пары параллельных ребер.

D

K 1

L 1

N 1

A

C

K

L

N

B

© Кузьмина Е.А., Колобовская МСОШ, 2010

Параллельные прямые в пространстве

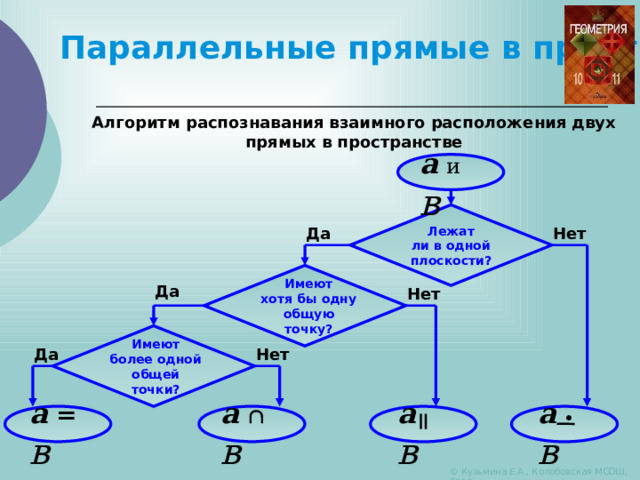
Алгоритм распознавания взаимного расположения двух прямых в пространстве

а и в

Лежат

ли в одной

плоскости?

Нет

Да

Имеют

хотя бы одну

общую

точку?

Да

Нет

Имеют

более одной

общей

точки?

Да

Нет

.

а в

а в

а  в

а = в

© Кузьмина Е.А., Колобовская МСОШ, 2010

Параллельные прямые в пространстве

Каково может быть взаимное расположение двух прямых в пространстве?

совпадают,

пересекаются,

параллельны,

скрещиваются

© Кузьмина Е.А., Колобовская МСОШ, 2010

Параллельные прямые в пространстве

5

Всегда ли две непересекающиеся прямые в пространстве параллельны?

6

Какие две прямые в пространстве называются параллельными?

а в

Дано: . Докажите, что все прямые, пересекающие данные лежат в одной плоскости.

7

8

Сколько можно провести в пространстве прямых, проходящих через данную точку, параллельных данной прямой?

© Кузьмина Е.А., Колобовская МСОШ, 2010

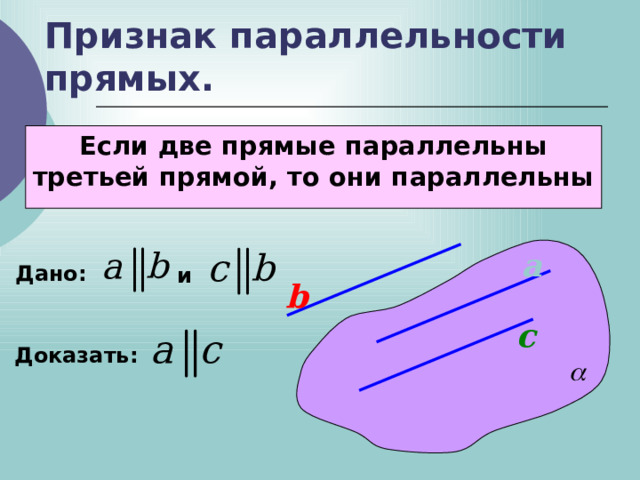
Признак параллельности прямых.

Если две прямые параллельны третьей прямой, то они параллельны

a

Дано:

и

b

с

Доказать:

H M

Задача 1

• Даны параллелограммы АВСД и АВМН не лежащие в одной плоскости.
• Доказать, что ДСМН тоже параллелограмм.

B C

А D

Задача 2.

Дано: М – середина BD

D

N – середина CD

Q – середина АС

P – середина АВ

M

АD = 12 см;

ВС = 14 см

N

A

Найти: 1) Какой фигурой является MNQP? 2) P MNQP

Р

B

Q

Ответ: 26 см.

C

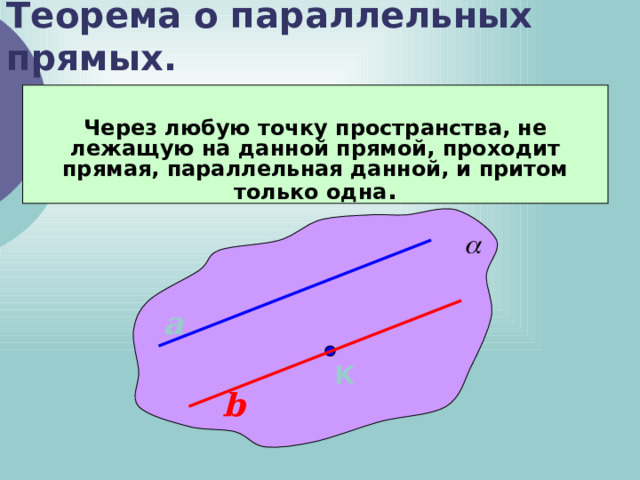
Теорема о параллельных прямых.

Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна .

a

К

b

Геометрия Лобачевского

Николай Иванович Лобачевский

Русский математик, создатель неевклидовой  геометрии, деятель университетского образования и народного просвещения.

Известный английский математик Уильям Клиффорд назвал Лобачевского «Коперником геометрии»

1835 г. вышел его мемуар

«Воображаемая геометрия»

Историческая справка

Среди аксиом Евклида была аксиома о параллельности прямых, а точнее,  пятый постулат о параллельных линиях :  если две прямые образуют с третьей по одну ее сторону внутренние углы, сумма которыҳ меньше развернутого угла, то такие прямые ᴨересекаются при достаточном продолжении с одной стороны . В современной формулировке она говорит о существовании  не более одной прямой, проходящей через данную точку вне данной прямой и параллельной этой данной прямой .

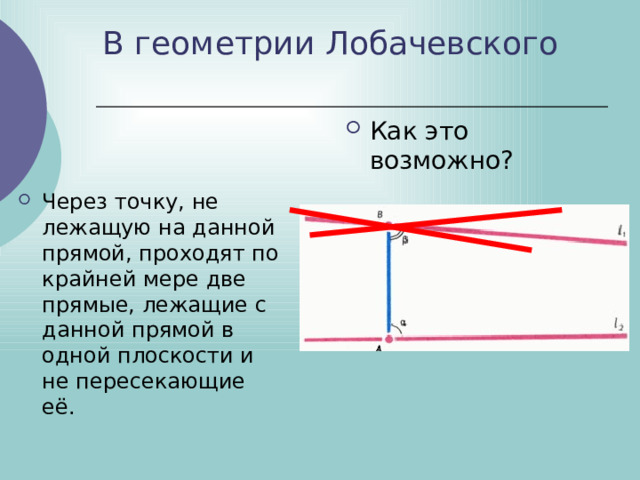
В геометрии Лобачевского

• Как это возможно?

• Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её.

Возможно, но не на обычной плоскости…

• Геометрия Лобачевского описывает не плоское пространство, как это делает геометрия Евклида, а оперирует понятиями гиперболического пространства

А

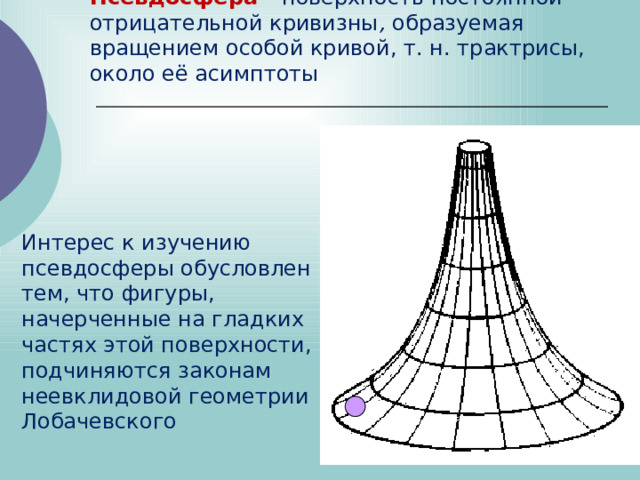
Псевдосфера - поверхность постоянной отрицательной кривизны ,  образуемая вращением особой кривой, т. н. трактрисы, около её асимптоты

Интерес к изучению псевдосферы обусловлен тем, что фигуры, начерченные на гладких частях этой поверхности, подчиняются законам неевклидовой геометрии Лобачевского

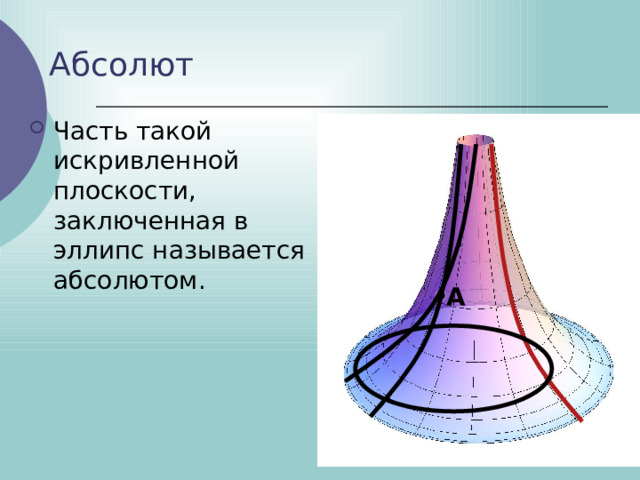
Абсолют

• Часть такой искривленной плоскости, заключенная в эллипс называется абсолютом.

А

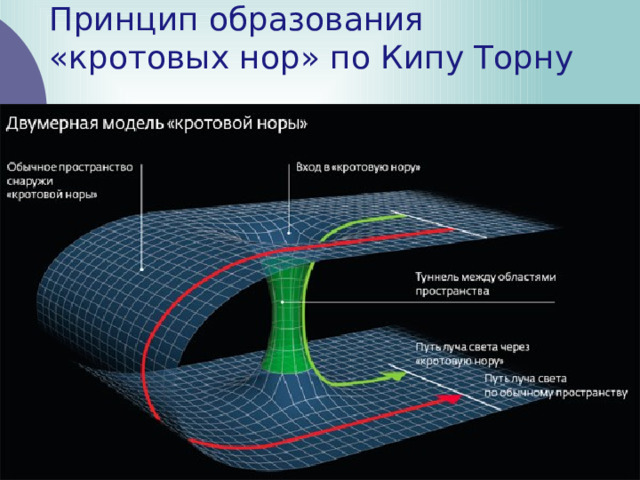
Принцип образования «кротовых нор» по Кипу Торну

Изобразите и сформулируйте

Определение параллельных прямых

Признак параллельности прямых

Домашнее задание

• 1) Учить конспекты по двум темам
• 2) Даны параллелограмм АВСД и трапеция АВЕК с основанием ЕК, не лежащие в одной плоскости. Выясните взаимное расположение прямых СД и ЕК