Взаимное расположение прямых в пространстве.

Крупное научное открытие дает решение крупной проблемы, но и в решении любой простой задачи присутствует крупица открытия.

• Задача, которую вы решаете, может быть скромной. И если она бросает вызов вашей любознательности, и заставляет вас быть изобретательным, и если вы решаете ее собственными силами, то вы сможете испытать ведущее к открытию напряжение ума, и насладиться радостью победы.

Повторим?

• 1. Утверждение, требующее доказательства.

----------------

• 2. утверждение, принимаемое без доказательства.

----------------

• 3. раздел геометрии, в котором изучаются фигуры в пространстве.

• 1. Теорема-

• 2. Аксиома –

• 3. Стереометрия -

Основные фигуры пространства.

• 1. точка

• 2. прямая

• 3. плоскость



а

• А

В

Аксиомы?



А

а



А В

С

Теоремы?

a b 

а

А





f

c

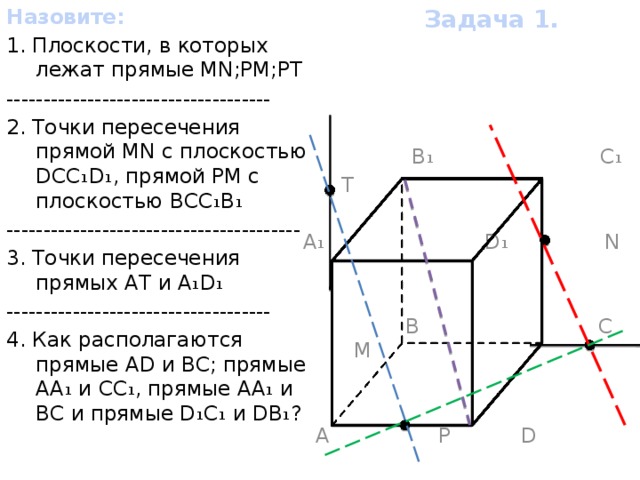
Задача 1.

Назовите:

1. Плоскости, в которых лежат прямые MN;PM;РТ

------------------------------------

2. Точки пересечения прямой MN с плоскостью DCC₁D₁, прямой PM с плоскостью BCC₁B₁

----------------------------------------

3. Точки пересечения прямых AT и A₁D₁

------------------------------------

4. Как располагаются прямые AD и BC; прямые AA₁ и CC₁, прямые АА₁ и ВС и прямые D₁C₁ и DB₁?

B₁ C₁

T

A₁ D₁ N

B C M

A P D

• Прямые пресекаются , тогда они лежат в одной плоскости и имеют одну общую точку.

2. Прямые параллельны , тогда они не имеют общих точек и лежат в одной плоскости.

3. Скрещивающиеся – прямые, которые не пересекаются и не параллельны.

Рассмотрим куб и отметим все варианты расположения прямых в пространстве.

Задача 2.

• Пересекаются ли прямые? Рассмотрим чертеж.

Признак параллельности прямых.

• Две прямые, параллельные третьей прямой, параллельны.

Задача 3.

Задача 4.

• Доказать, что все прямые, пересекающие две данные параллельные прямые, лежат в одной плоскости.

• Если ABCD и ABC ' D ' - параллелограммы, то доказать, что и CC ' D ' D - параллелограмм.

Домашнее задание.

• Концы отрезка отстоят от плоскости на расстояние 30 и 40 см. Рассмотреть всевозможные случаи расположения отрезка и плоскости.

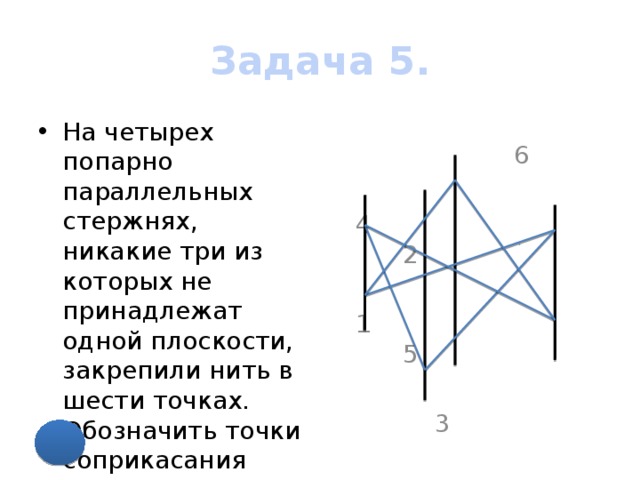
Задача 5.

• На четырех попарно параллельных стержнях, никакие три из которых не принадлежат одной плоскости, закрепили нить в шести точках. Обозначить точки соприкасания нитей.

6

4 2

1 5

3

Но один вопрос мучает меня вновь и вновь: «Да, если решение, по-видимому, достигает цели и кажется верным, то как можно придумать такое решение? Каким образом ты сам мог бы придумать или открыть подобные вещи?»

Рефлексия.

• Какие цели я ставила перед вами?

---------------------------

• Как вы думаете, мы их выполнили?

• Как могут располагаться прямые в пространстве?

-----------------------

2. Определение пересекающихся прямых?

--------------------------

3. Сформулируйте определение параллельных прямых.

---------------------

4. Сформулируйте понятие скрещивающихся прямых?

---------------------

5. Признак параллельности прямых?

---------------------

7. Так о чем мы вели разговор? Тема урока?

Взаимное расположение прямых в пространстве.

Желаю не смотреть на математику как на предмет, по которому ты должен получить столько-то зачетов и который ты постараешься забыть как можно быстрее после последнего экзамена.

Спасибо за урок!