Зачет по теме "Треугольники" (7 класс)

Сильное желание чему-то научиться - это уже 50% успеха.

Дейл Карнеги

Зачет по геометрии по теме: «Треугольники»

Вариант 1.

Это просто очередная проверка твоих знаний. Спокойствия и веры тебе желаю. Ты успешно все сдашь, я верю в тебя!

1. Тестовая часть:

1. Что из перечисленного является элементами треугольника?

Выберите несколько из 3 вариантов ответа:

1) стороны; 2) углы; 3) периметр.

2. Продолжите предложение: "В равных треугольниках против соответственно равных сторон лежат ... ".

Выберите один из 3 вариантов ответа:

1) равные стороны; 2) равные стороны и углы; 3) равные углы.

3. Треугольник является тупоугольным, если …

Выберите один из 3 вариантов ответа:

1) среди его углов нет тупого; 2) каждый его угол меньше тупого;

3) если один из его углов тупой.

2. Теоретический опрос:

1. Сформулируйте теорему, выражающую второй признак равенства треугольников.

1. Сформулируйте утверждение о медиане равнобедренного треугольника.

1. Какой отрезок называется высотой треугольника? Сколько высот имеет треугольник?

1. Какой треугольник называется равнобедренным? Перечислите его свойства.

Сильное желание чему-то научиться - это уже 50% успеха.

Дейл Карнеги

Зачет по геометрии по теме: «Треугольники»

Вариант 2.

Это просто очередная проверка твоих знаний. Спокойствия и веры тебе желаю. Ты успешно все сдашь, я верю в тебя!

1. Тестовая часть:

1. Треугольник является остроугольным, если …

Выберите один из 3 вариантов ответа:

1) среди его углов нет тупого; 2) каждый его угол меньше тупого;

3) если все его углы острые.

2. Что из перечисленного является элементами треугольника?

Выберите несколько из 3 вариантов ответа:

1) диагонали; 2) углы; 3) стороны.

3. Продолжите предложение: "В равных треугольниках против соответственно равных углов лежат соответственно ... ".

Выберите один из 3 вариантов ответа:

1) равные стороны; 2) равные стороны и углы; 3) равные углы.

2. Теоретический опрос:

1. Сформулируйте теорему, выражающую первый признак равенства треугольников.

1. Сформулируйте утверждение о высоте равнобедренного треугольника.

1. Какой отрезок называется биссектрисой треугольника? Сколько биссектрис имеет треугольник?

1. Какой треугольник называется равносторонним? Перечислите свойства равностороннего треугольника.

3. Ответьте «да» или «нет»:

1) Треугольник равносторонний, то все его стороны равны.

2) В равнобедренном треугольнике медиана является высотой и биссектрисой.

3) Высота треугольника, опущенная из данной вершины – это перпендикуляр, проведённый из данной вершины к прямой содержащей противолежащую сторону.

4) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.

5) Прямую, перпендикулярную отрезку называют серединным перпендикуляром отрезка.

4. Выпишите к каждой цифре соответствующие буквы:

1) Треугольники равны по 1 признаку:

2) Треугольники равны по 2 признаку:

3) Треугольники равны по 3 признаку:

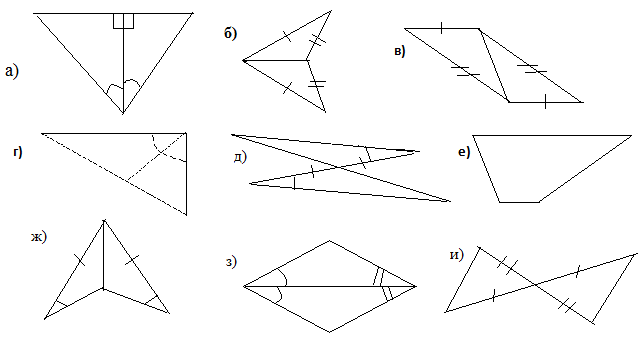
3. Ответьте «да» или «нет»:

1) В разностороннем треугольнике все стороны разной длины.

2) В равнобедренном треугольнике медиана, проведенная к основанию является только биссектрисой.

3) Из точки, не лежащей на прямой, можно провести единственный перпендикуляр к этой прямой.

4) В любом треугольнике биссектрисы пересекаются в одной точке.

5) В равных треугольниках против равных сторон лежат равные углы.

4. Выпишите к каждой цифре соответствующие буквы:

1) Треугольники равны по 1 признаку:

2) Треугольники равны по 2 признаку:

3) Треугольники равны по 3 признаку:

\
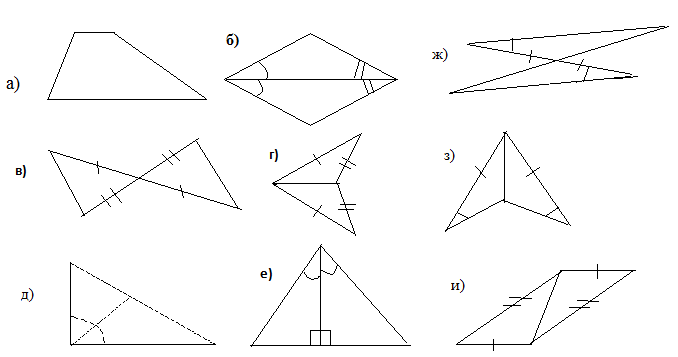