| Вариант №1 Используя основное тригонометрическое тождество, вычислить sin α, tg α, сtg α, если cosα = 0,8. 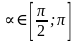 . . Дописать формулу: sin2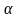 = = tg = 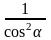 = =
cos (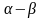 )= )= sin2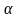 = = sin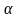 + sin + sin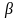 = = sin 600= cos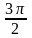 = = cos 450= Знаки тригонометрических функций : 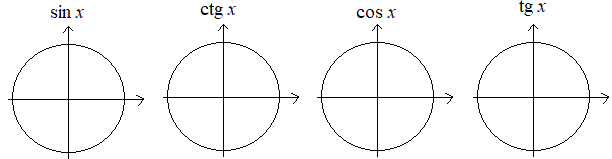
Записать ответ, используя формулу приведения: 1) cos(π + x)= 2) sin(½π – x)= 3) tg(2π + x)= 4) ctg(3/2π –x)= 5. Указать табличные значения тригонометрических функций для углов 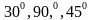 . . 6. Записать формулы сложения для косинуса. 7. Из формулы 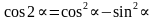 , выразить косинус двойного угла через синус. , выразить косинус двойного угла через синус. 8. ДОКАЗАТЬ ТОЖДЕСТВО: cos2 (α - β) - cos2 (α + β) = tg α . tg β 4 cos2 α cos2 β 9. УПРОСТИТЬ: 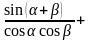 tg β . tg β . 10. Вычислить: 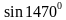 . . 11. ВЫЧИСЛИТЬ, ИСПОЛЬЗУЯ ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФОРМУЛЫ: (cos 150 + sin 150)2 . | Вариант №2 Используя основное тригонометрическое тождество, вычислить cosα, tg α, сtg α, если sin α = 0,6. 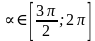 . . Дописать формулу: cos 2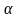 = = ctg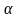 = = 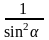 = =
sin (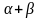 )= )= cos 2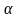 = = cos 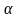 + cos + cos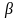 = = cos 600= cos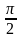 = = sin 450= Знаки тригонометрических функций : 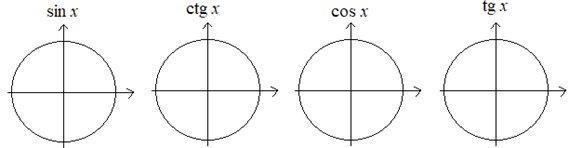
Записать ответ, используя формулу приведения: 1) cos(½π – x)= 2) sin(π–x)= 3) tg(3/2π –x)= 4) ctg(2π - x)= 5. Указать табличные значения тригонометрических функций для углов 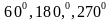 . . 6. Записать формулы сложения для синуса. 7. Из формулы 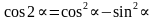 , выразить косинус двойного угла через косинус. , выразить косинус двойного угла через косинус. 8. ДОКАЗАТЬ ТОЖДЕСТВО: sin α + tg α == tg α 1 + cos α 9. УПРОСТИТЬ: 10. Вычислить:  . . 11. ВЫЧИСЛИТЬ, ИСПОЛЬЗУЯ ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФОРМУЛЫ: cos 270 cos 180 - sin 270 sin 180.
9
|
|







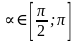 .
.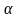 =
=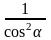 =
= 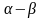 )=
)=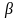 =
=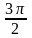 =
=
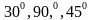 .
.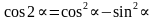 , выразить косинус двойного угла через синус.
, выразить косинус двойного угла через синус.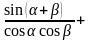 tg β .
tg β .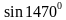 .
.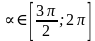 .
.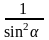 =
=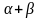 )=
)=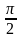 =
=
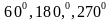 .
.









