Зачет по теме «Векторы в пространстве» (Геометрия, 10 класс)
 Вариант 1
Вариант 1
- а) Сформулируйте понятие коллинеарных векторов;
На рис.1 изображен параллелепипед. Выпишете:
б) 5 векторов, противоположно направленных к  ;
;
в) 5 векторов, сонаправленных с  ;
;
г) 2 вектора, равных  .
.
- Нарисуйте тетраэдр DABC. Изобразите на рисунке векторы:
а)  ; б)
; б)  ; в)
; в)  .
.
 Скопируйте векторы с рис. 2 в тетрадь и постройте векторы:
Скопируйте векторы с рис. 2 в тетрадь и постройте векторы:
 а)
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
 Перечислите свойства умножения вектора на число: сочета-тельное, первое и второе распределительные свойства.
Перечислите свойства умножения вектора на число: сочета-тельное, первое и второе распределительные свойства.- Упростите выражения: а)
 ;
;
 б)
б)  ; в)
; в)  .
.
- Дан параллелепипед ABCDA1B1C1D1 (рис.1). Какие из трех следующих векторов компланарны: а)
 ; б)
; б)  ; в)
; в)  ; г)
; г)  ?
?
- Выразите векторы
 на рис. 3 через векторы
на рис. 3 через векторы 
 , если известно, что Y – середина DB, а DХ =
, если известно, что Y – середина DB, а DХ =  DC.
DC.
Зачет по теме «Векторы в пространстве»
Вариант 2

- На рис.1 изображен параллелепипед. Выпишете:
а) 5 векторов, сонаправленных с  ;
;
б) 5 векторов, противоположно направленных к  ;
;
в) Сформулируйте понятие равных векторов;
г) 2 вектора, равных  .
.
- Нарисуйте тетраэдр DABC. Изобразите на рисунке векторы:
а)  ; б)
; б)  ; в)
; в)  .
.
 Скопируйте векторы с рис. 2 в тетрадь и постройте векторы:
Скопируйте векторы с рис. 2 в тетрадь и постройте векторы:

 а)
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
- Запишите в буквенном виде переместительное и сочетательное свойства сложения векторов.
 Упростите выражения: а)
Упростите выражения: а)  ; б)
; б) ; в)
; в) .
.- Дан параллелепипед ABCDA1B1C1D1 (рис.1). Какие из трех следую-щих векторов компланарны: а)
 ; б)
; б)  ; в)
; в)  ; г)
; г)  ?
?
- Выразите векторы
 на рис. 3 через векторы
на рис. 3 через векторы  ,
,  , если известно, что N – середина AC, а DM =
, если известно, что N – середина AC, а DM =  DC.
DC.
Просмотр содержимого документа
«Зачет по теме " Векторы в пространстве"»
Зачет по теме «Векторы в пространстве» (Геометрия, 10 класс)
В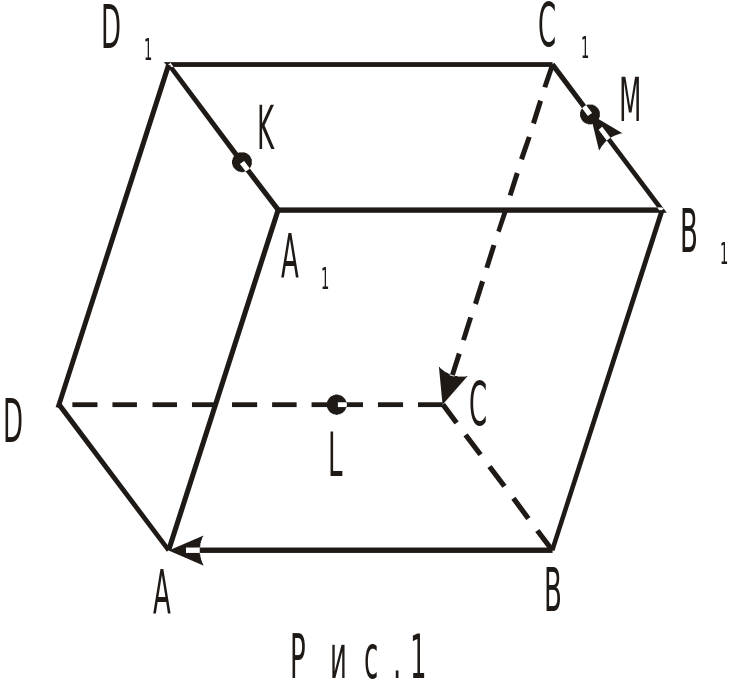 ариант 1
ариант 1
а) Сформулируйте понятие коллинеарных векторов;
На рис.1 изображен параллелепипед. Выпишете:
б) 5 векторов, противоположно направленных к 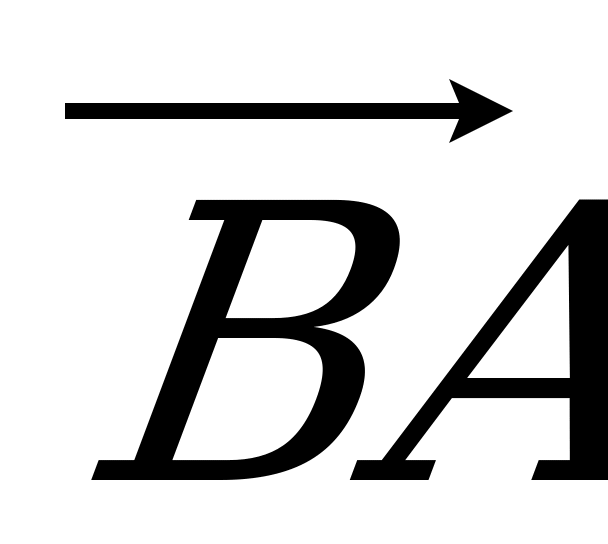 ;
;
в) 5 векторов, сонаправленных с 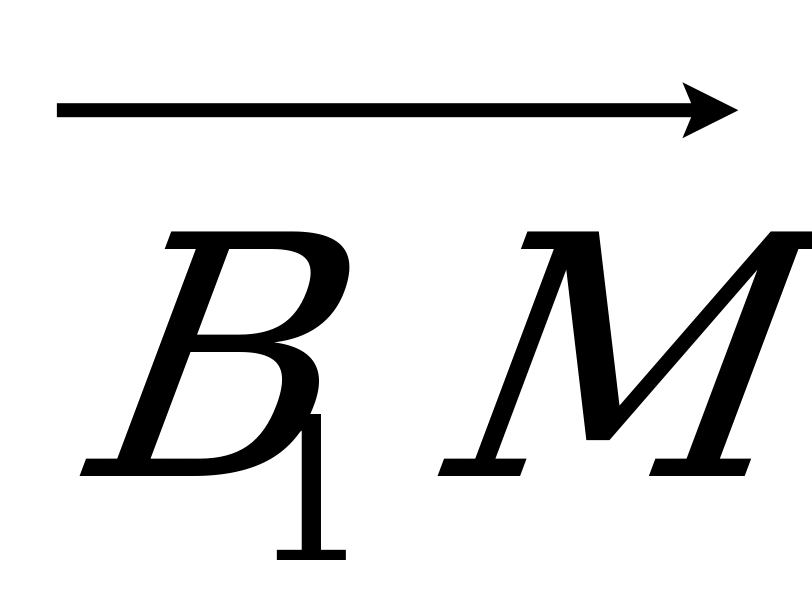 ;
;
г) 2 вектора, равных 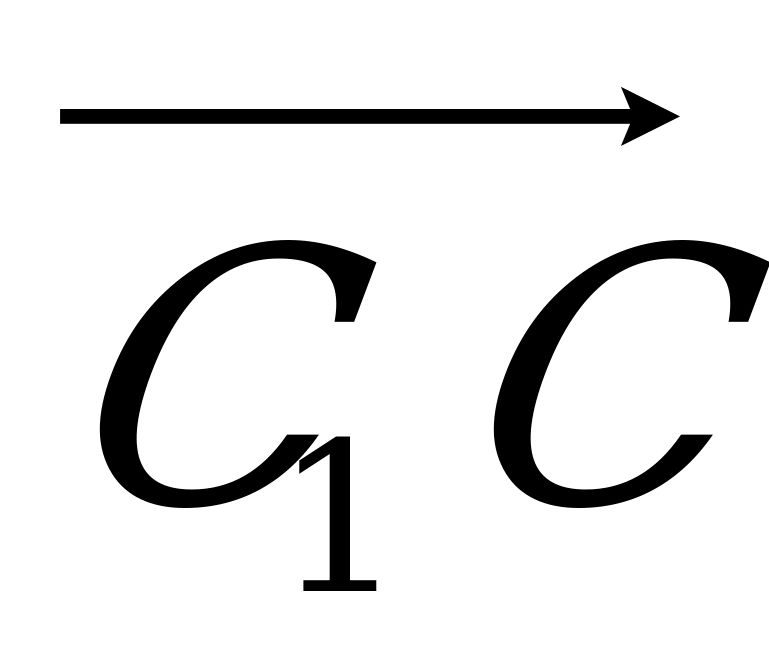 .
.
Нарисуйте тетраэдр DABC. Изобразите на рисунке векторы:
а) 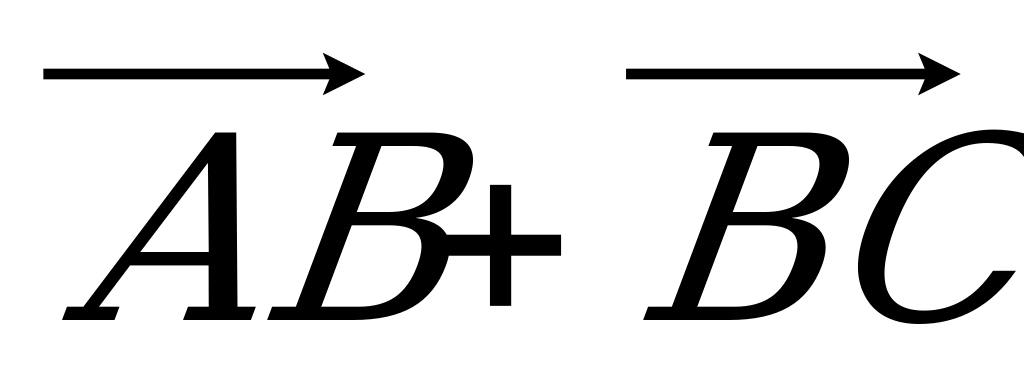 ; б)
; б) 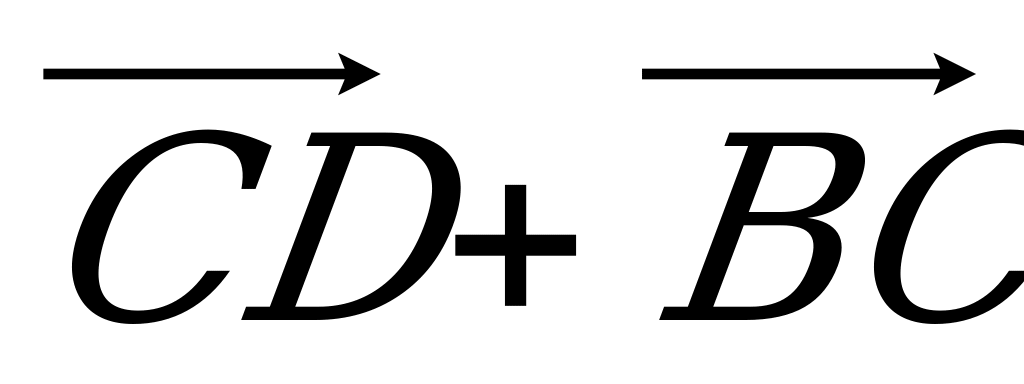 ; в)
; в) 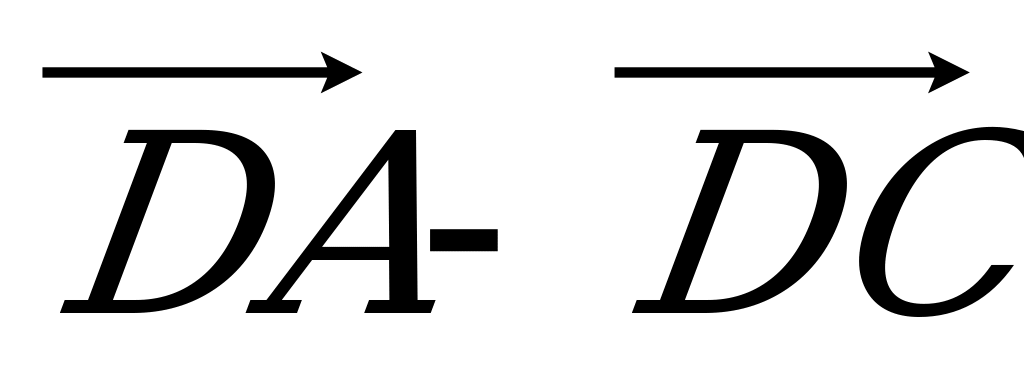 .
.
С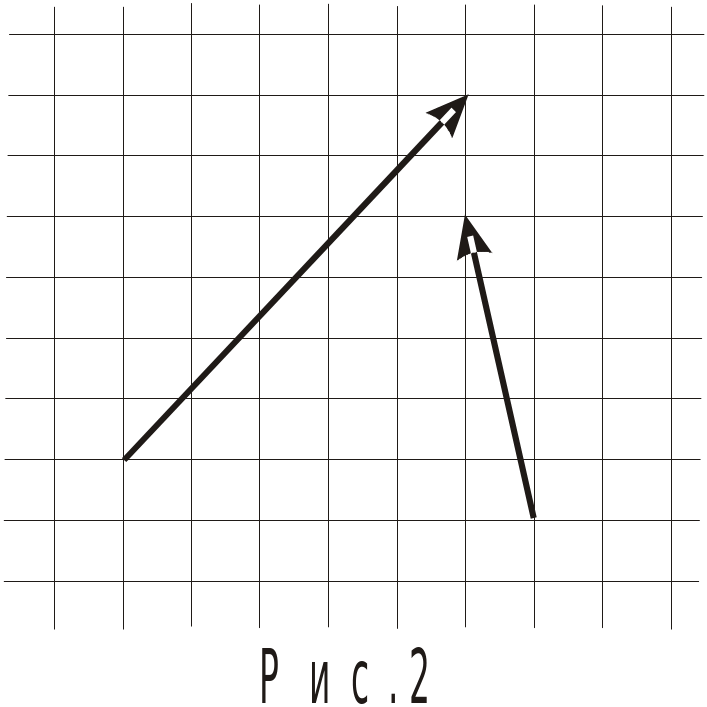 копируйте векторы с рис. 2 в тетрадь и постройте векторы:
копируйте векторы с рис. 2 в тетрадь и постройте векторы:
а
a
)
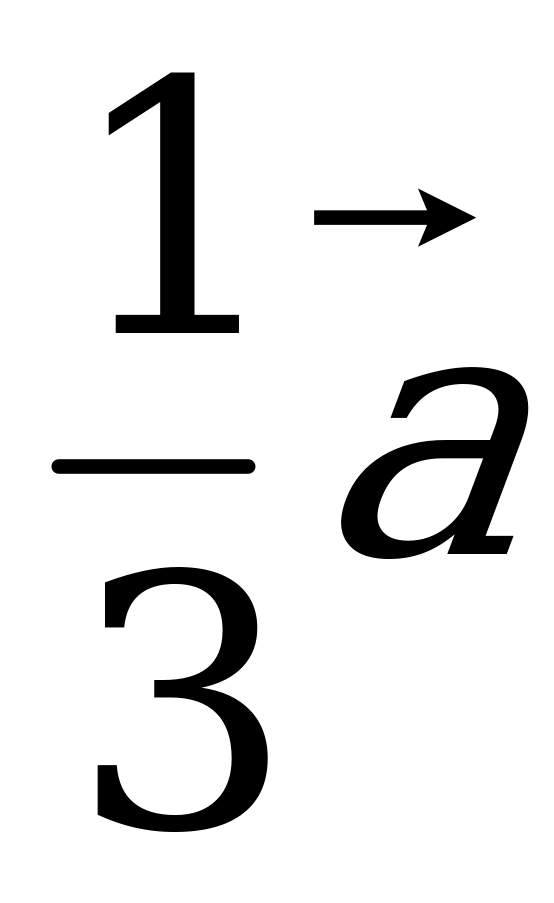
; б)
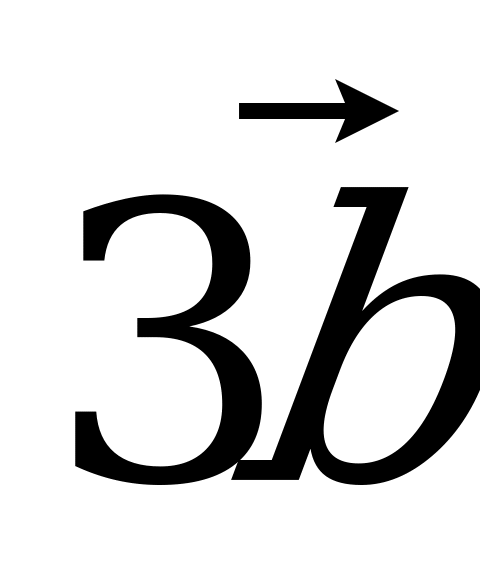
; в)
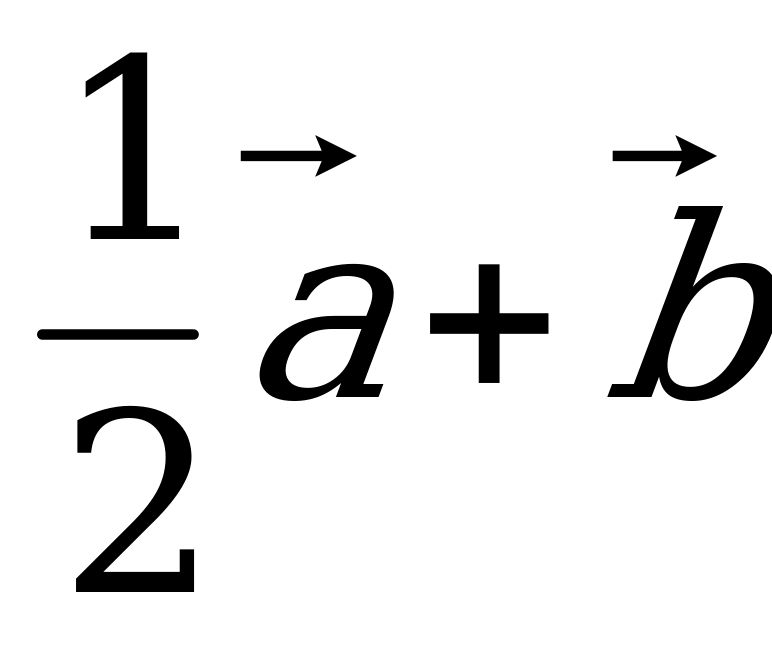
; г)
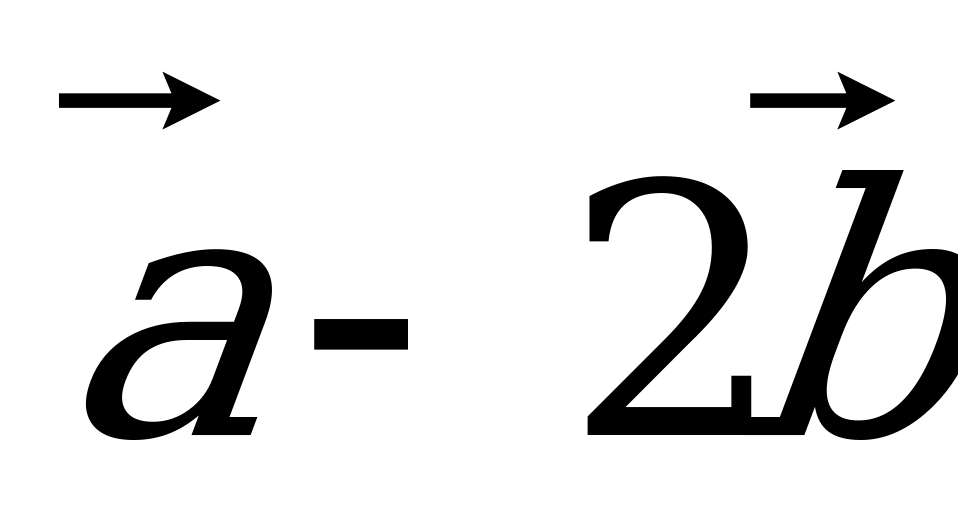
.
П
b
еречислите свойства умножения вектора на число: сочета-тельное, первое и второе распределительные свойства. Упростите выражения: а) 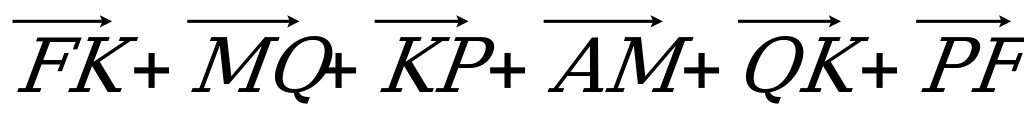 ;
;
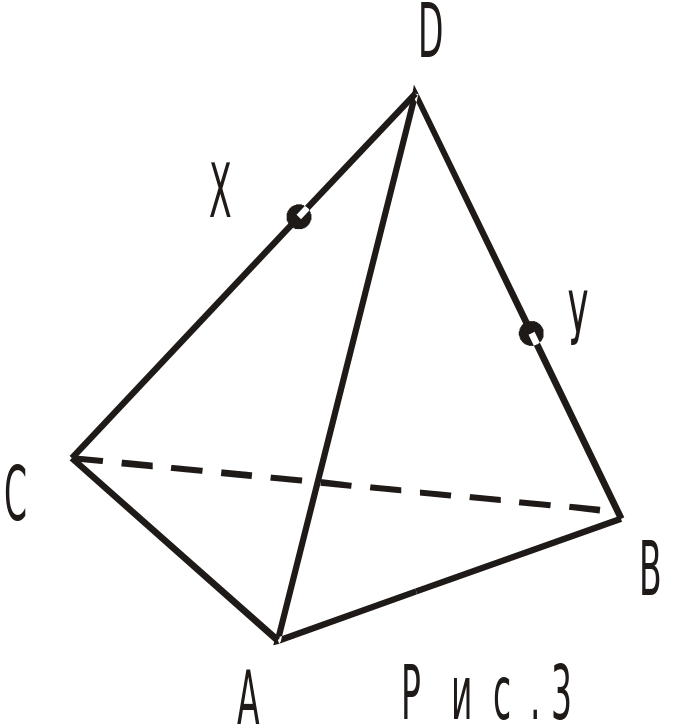 б)
б) 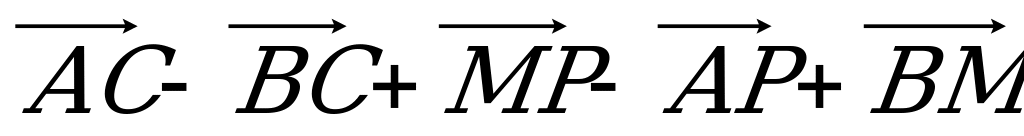 ; в)
; в) 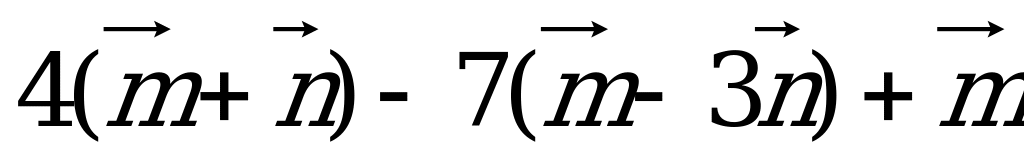 .
.
Дан параллелепипед ABCDA1B1C1D1 (рис.1). Какие из трех следующих векторов компланарны: а) 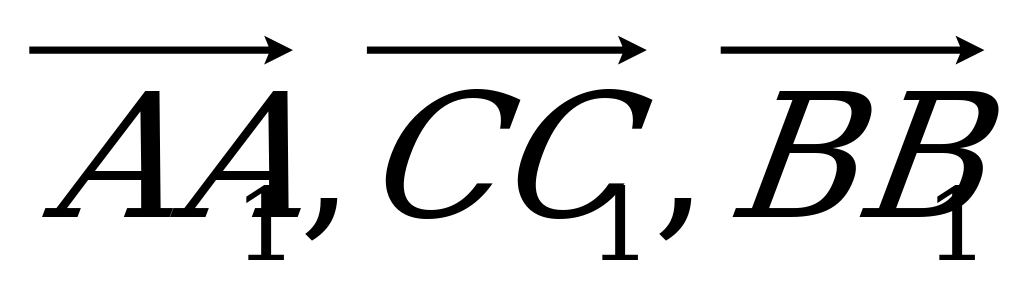 ; б)
; б)  ; в)
; в)  ; г)
; г) 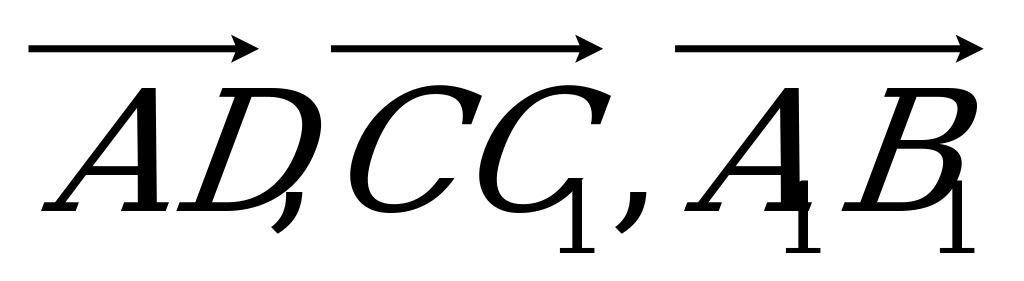 ?
?
Выразите векторы 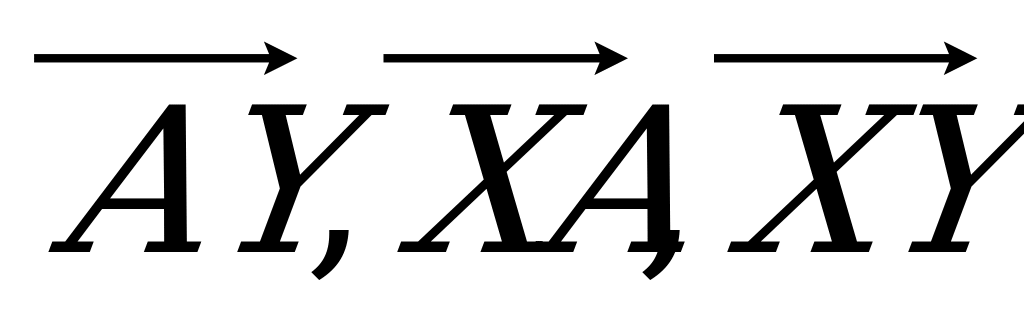 на рис. 3 через векторы
на рис. 3 через векторы 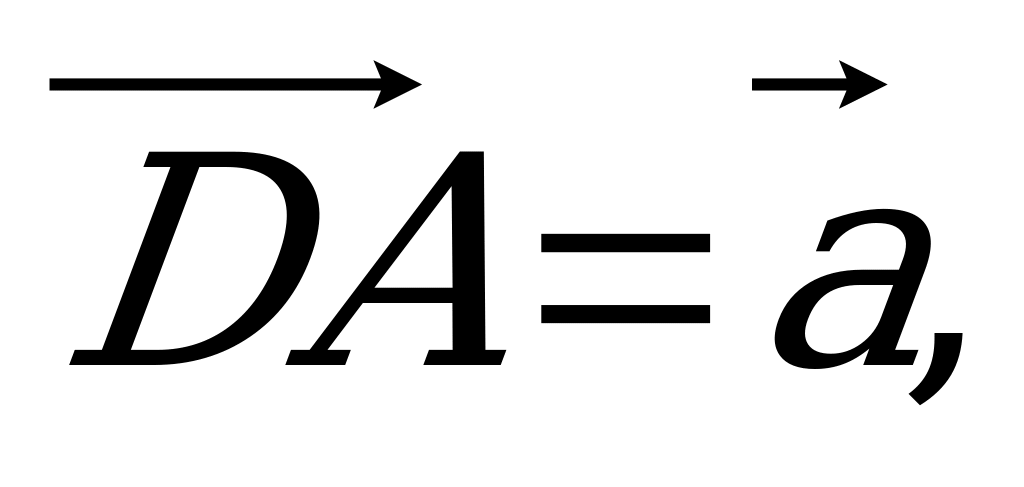
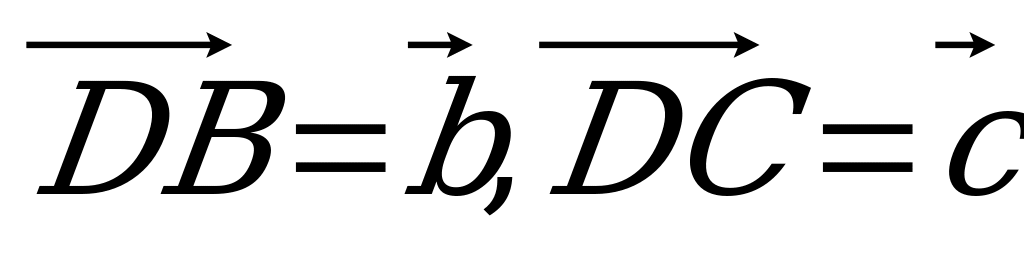 , если известно, что Y – середина DB, а DХ =
, если известно, что Y – середина DB, а DХ = 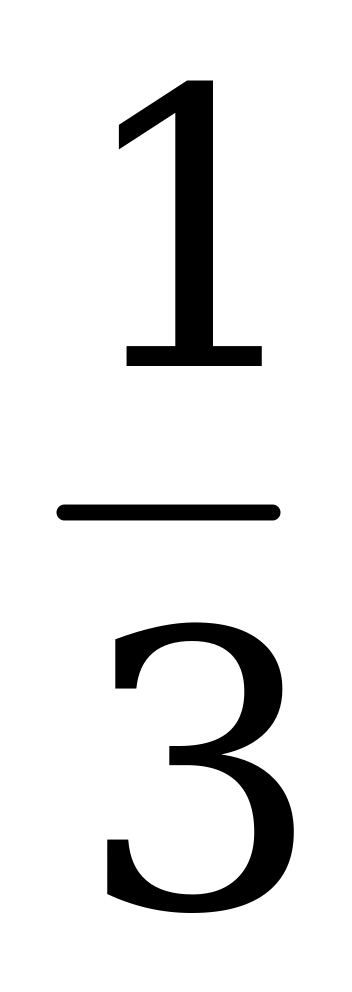 DC.
DC.
Зачет по теме «Векторы в пространстве»
Вариант 2
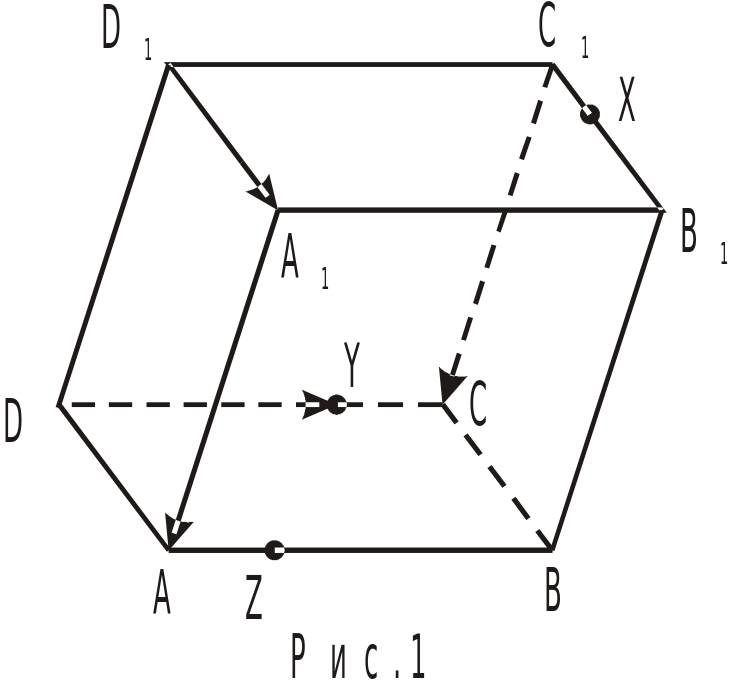
На рис.1 изображен параллелепипед. Выпишете:
а) 5 векторов, сонаправленных с  ;
;
б) 5 векторов, противоположно направленных к 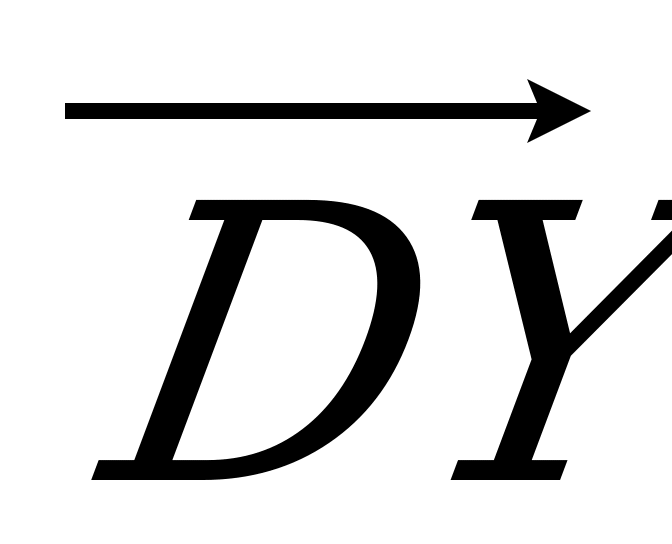 ;
;
в) Сформулируйте понятие равных векторов;
г) 2 вектора, равных 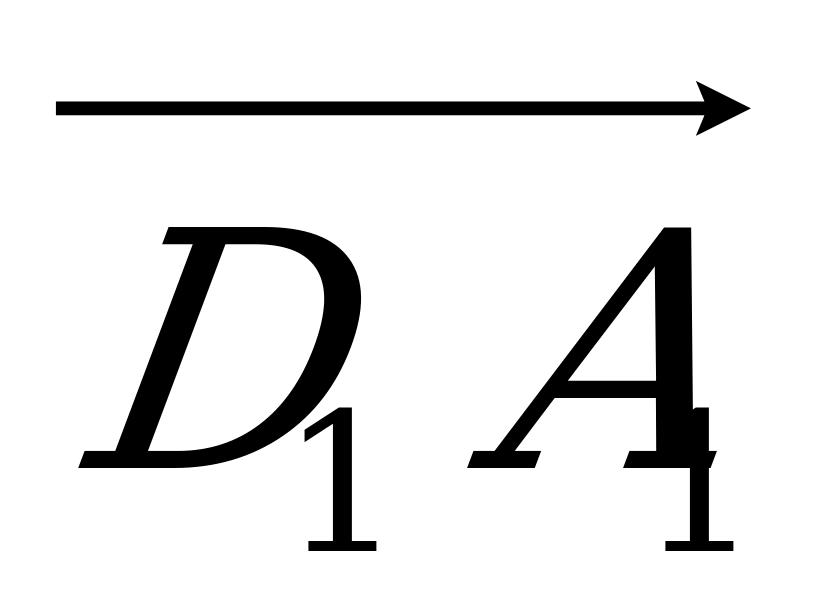 .
.
Нарисуйте тетраэдр DABC. Изобразите на рисунке векторы:
а) 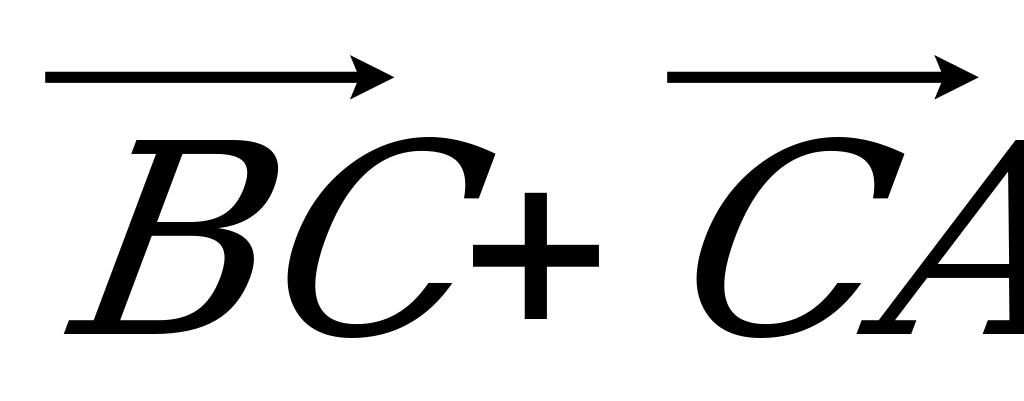 ; б)
; б) 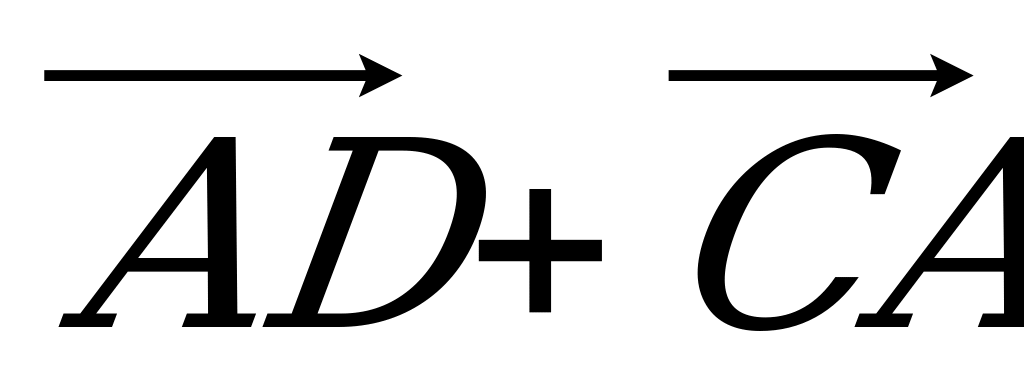 ; в)
; в) 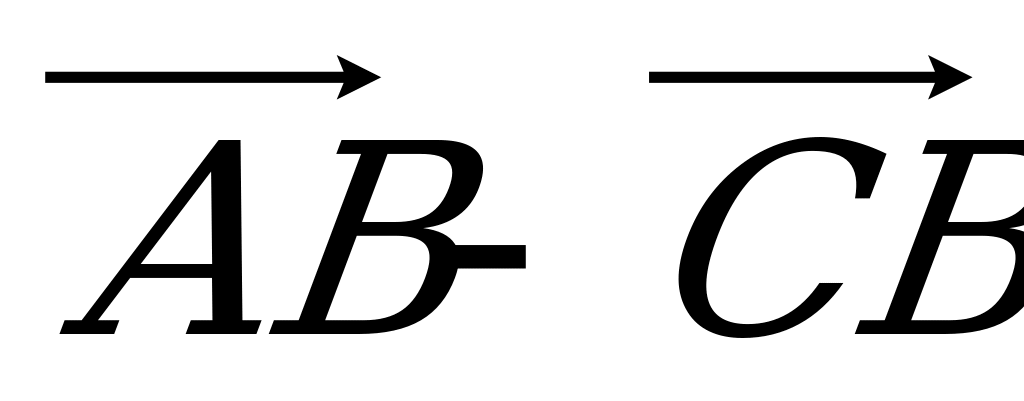 .
.
С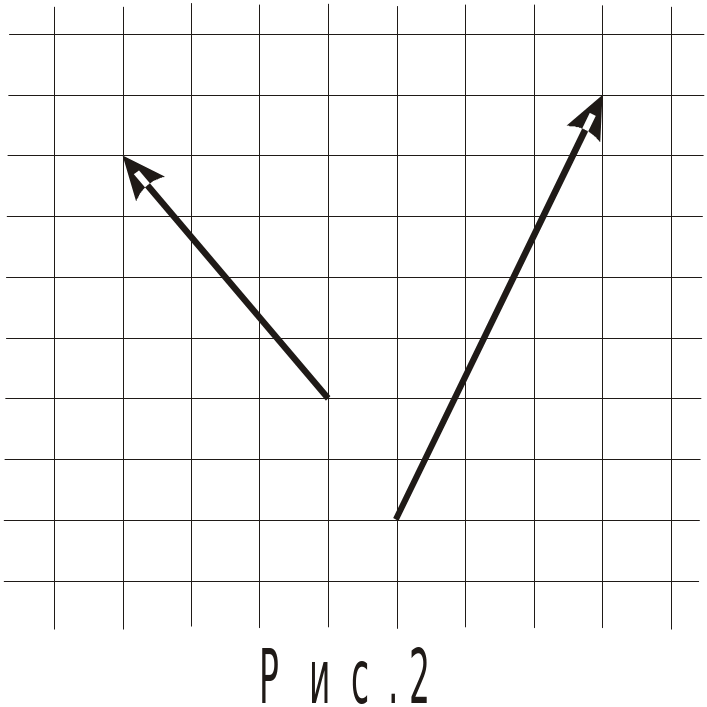 копируйте векторы с рис. 2 в тетрадь и постройте векторы:
копируйте векторы с рис. 2 в тетрадь и постройте векторы:
а
a
b
)
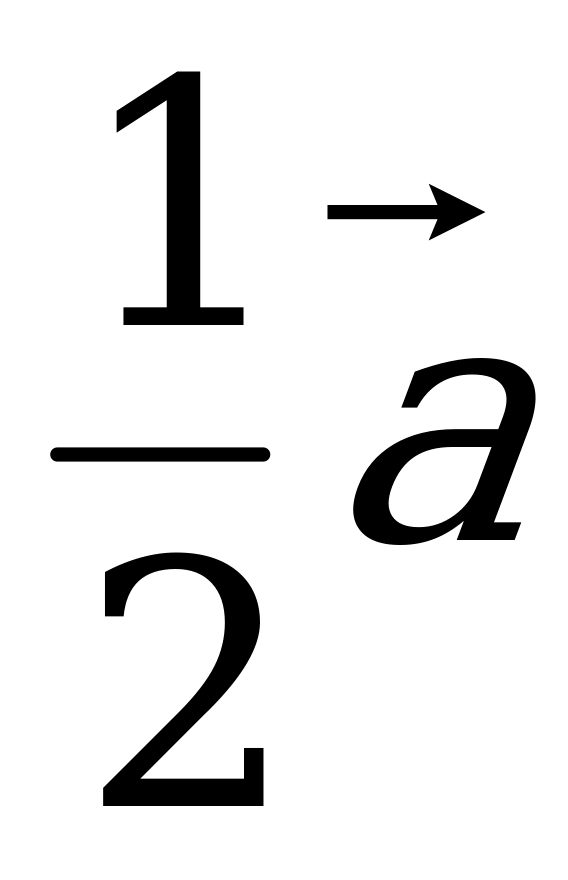
; б)
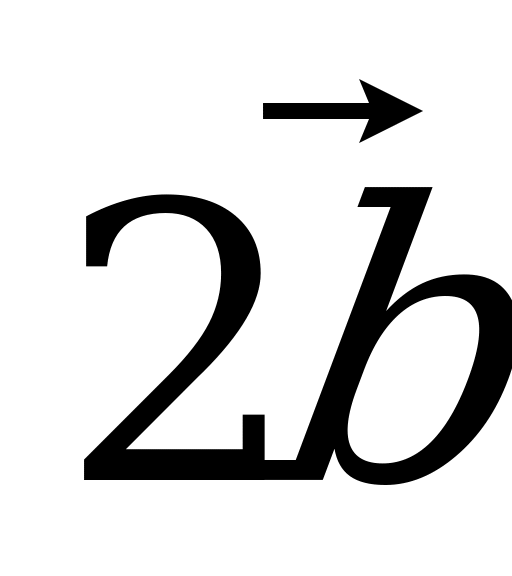
; в)
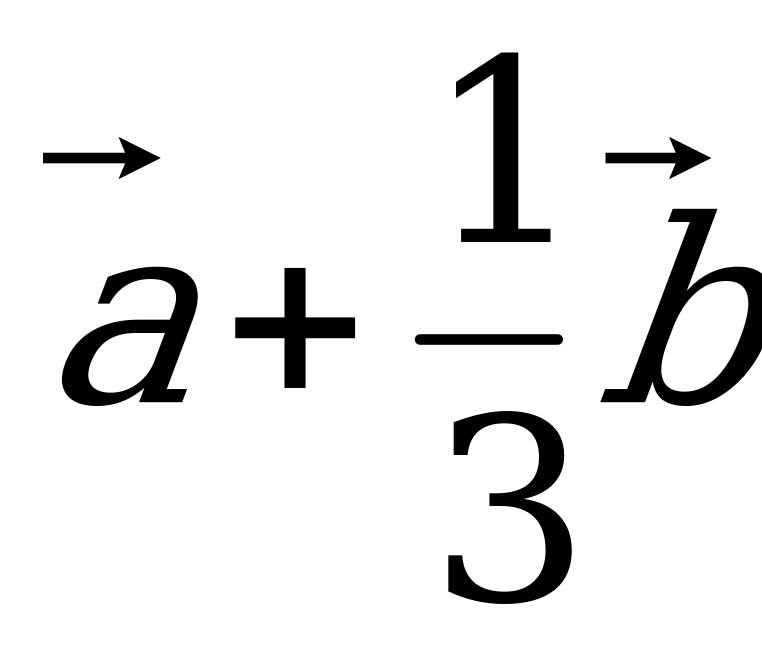
; г)
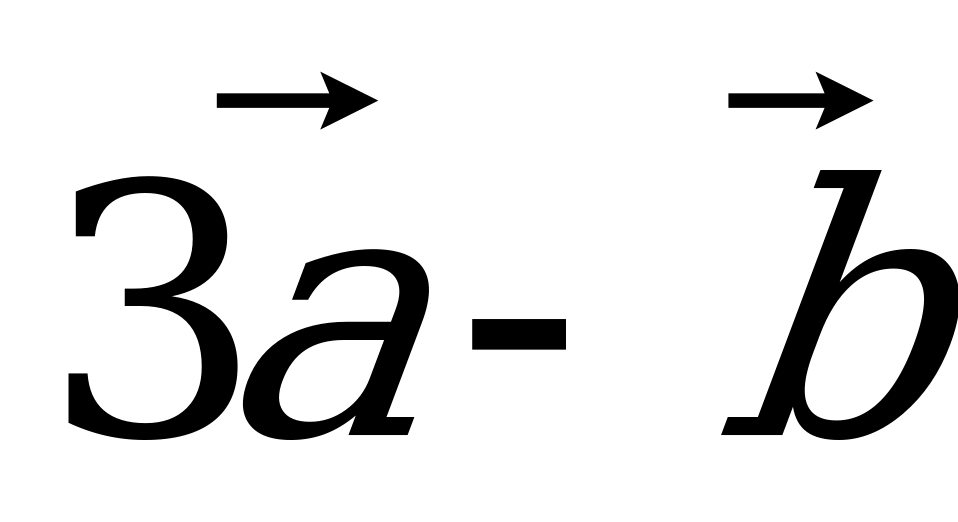
.
Запишите в буквенном виде переместительное и сочетательное свойства сложения векторов.
У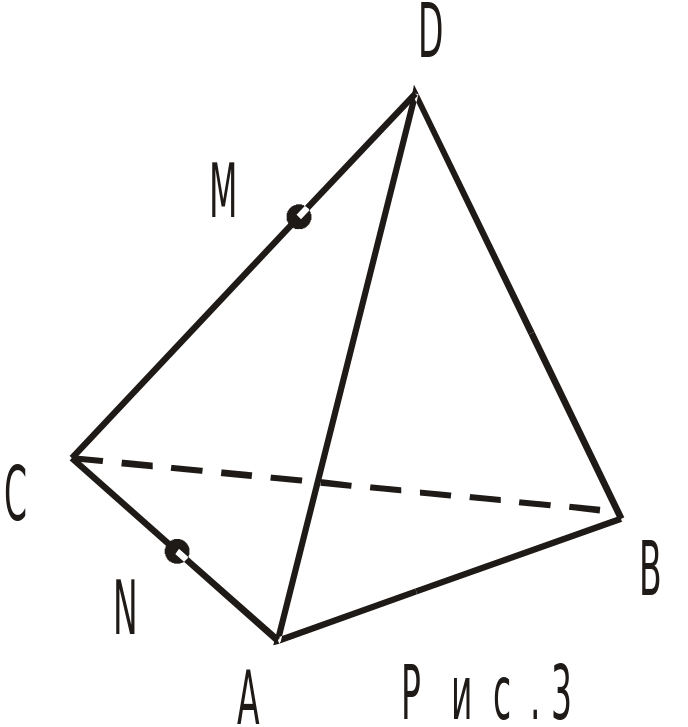 простите выражения: а)
простите выражения: а) 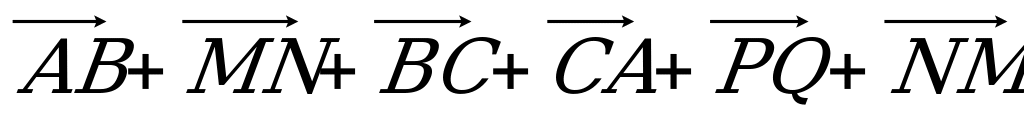 ; б)
; б) ; в)
; в)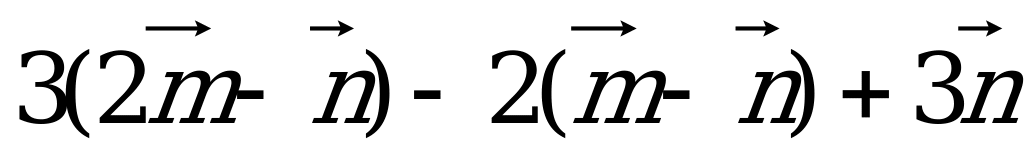 .
.
Дан параллелепипед ABCDA1B1C1D1 (рис.1). Какие из трех следую-щих векторов компланарны: а) 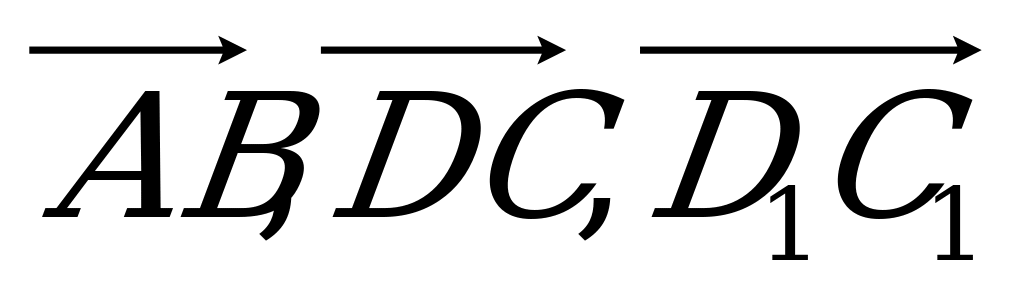 ; б)
; б) 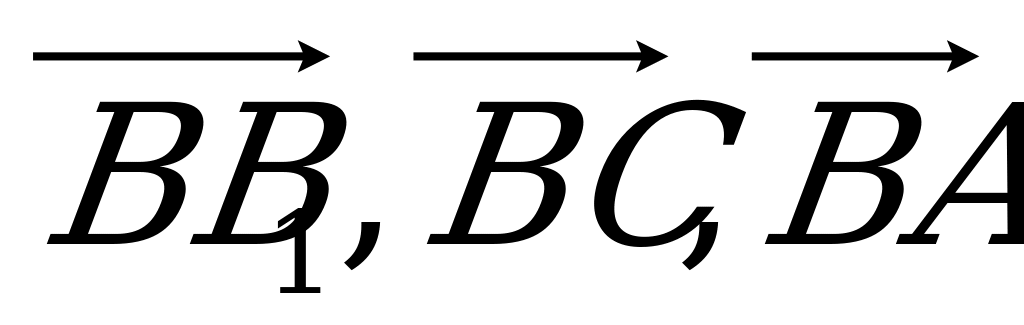 ; в)
; в) 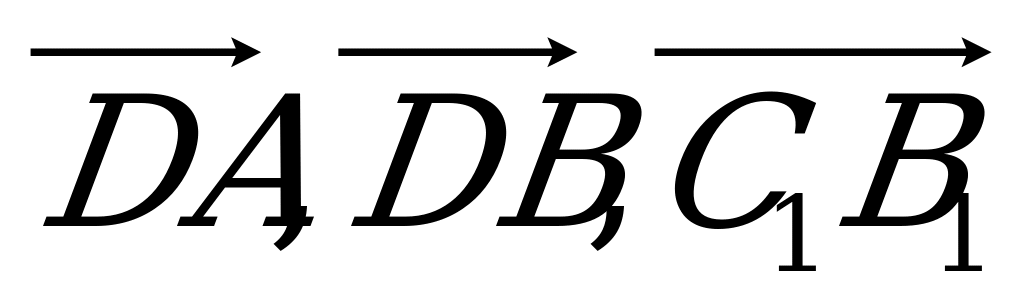 ; г)
; г) 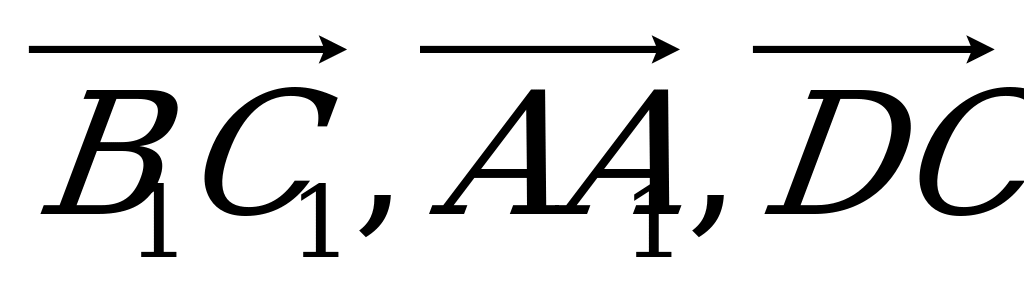 ?
?
Выразите векторы 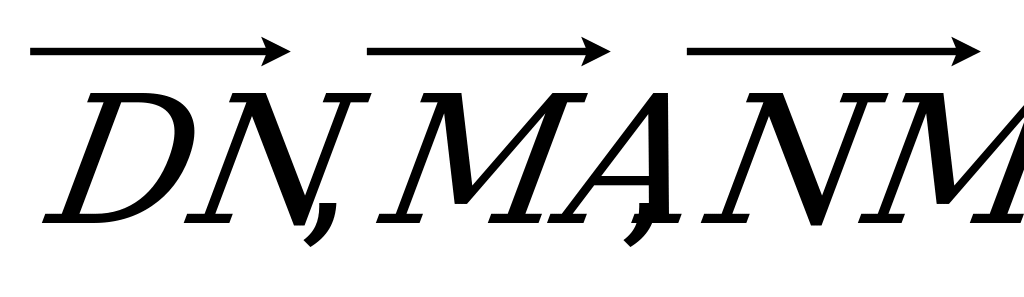 на рис. 3 через векторы
на рис. 3 через векторы 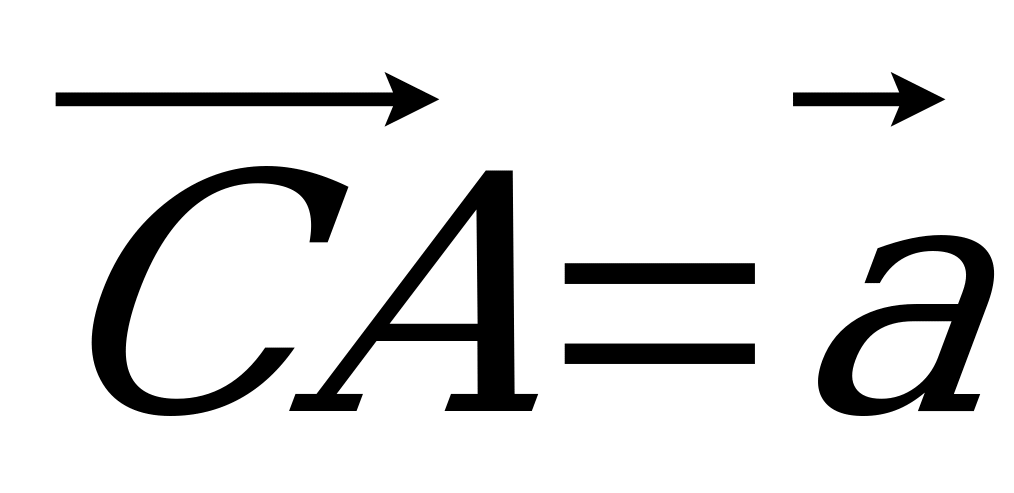 ,
, 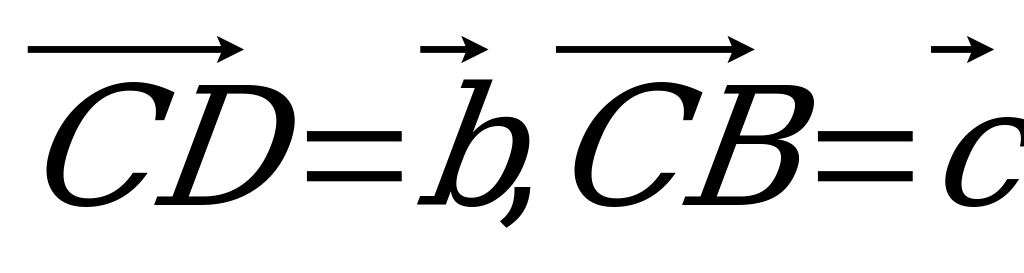 , если известно, что N – середина AC, а DM =
, если известно, что N – середина AC, а DM = 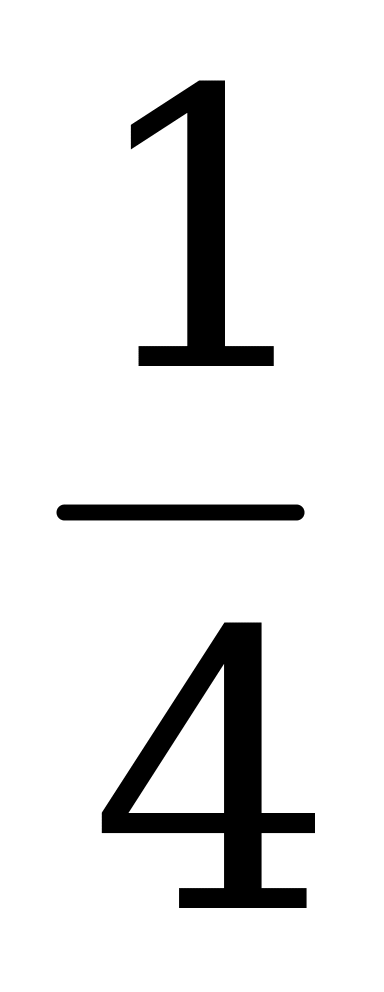 DC.
DC.






 Вариант 1
Вариант 1 ;
; ;
; .
. ; б)
; б)  ; в)
; в)  .
. Скопируйте векторы с рис. 2 в тетрадь и постройте векторы:
Скопируйте векторы с рис. 2 в тетрадь и постройте векторы: а)
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. Перечислите свойства умножения вектора на число: сочета-тельное, первое и второе распределительные свойства.
Перечислите свойства умножения вектора на число: сочета-тельное, первое и второе распределительные свойства. ;
;  б)
б)  ; в)
; в)  .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  ?
? на рис. 3 через векторы
на рис. 3 через векторы 
 , если известно, что Y – середина DB, а DХ =
, если известно, что Y – середина DB, а DХ =  DC.
DC.
 ;
; ;
; .
. ; б)
; б)  ; в)
; в)  .
. Скопируйте векторы с рис. 2 в тетрадь и постройте векторы:
Скопируйте векторы с рис. 2 в тетрадь и постройте векторы:
 а)
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
. Упростите выражения: а)
Упростите выражения: а)  ; б)
; б) ; в)
; в) .
. ; б)
; б)  ; в)
; в)  ; г)
; г)  ?
? на рис. 3 через векторы
на рис. 3 через векторы  ,
,  , если известно, что N – середина AC, а DM =
, если известно, что N – середина AC, а DM =  DC.
DC. ариант 1
ариант 1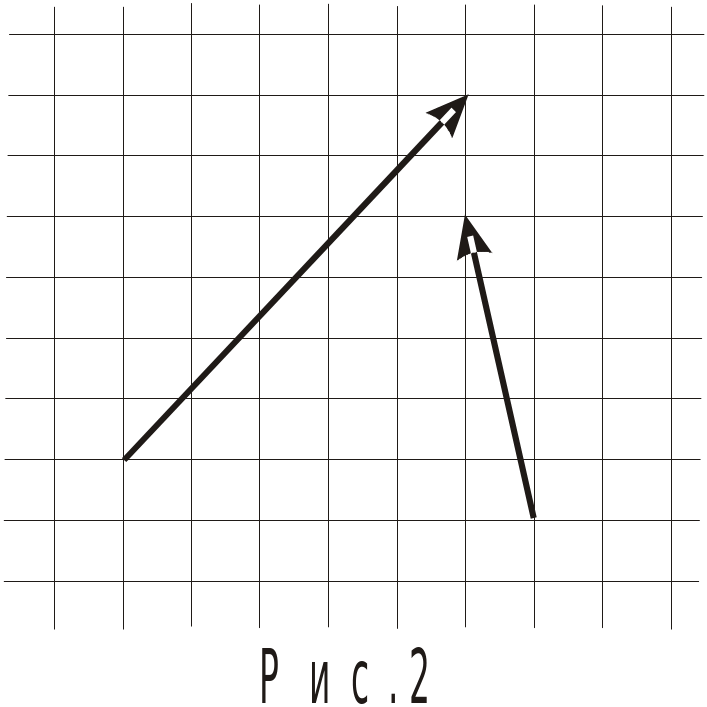 копируйте векторы с рис. 2 в тетрадь и постройте векторы:
копируйте векторы с рис. 2 в тетрадь и постройте векторы: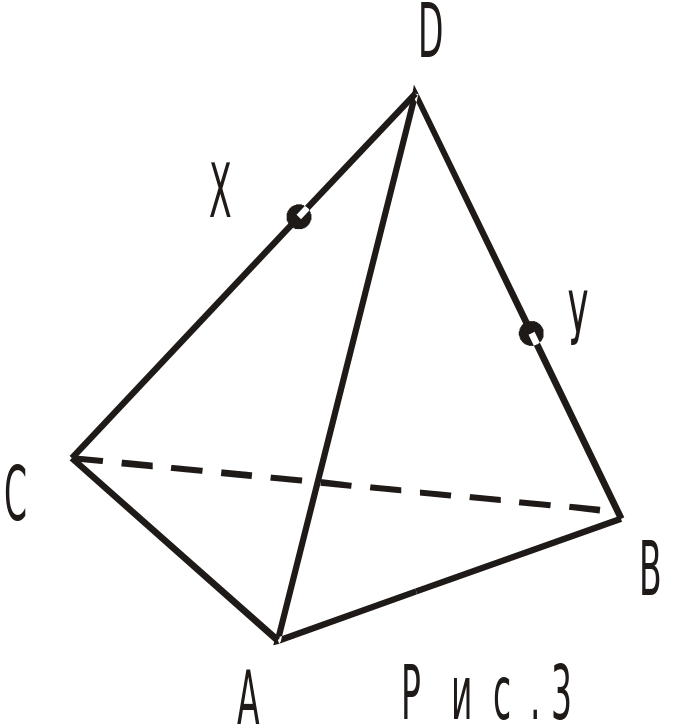 б)
б) 
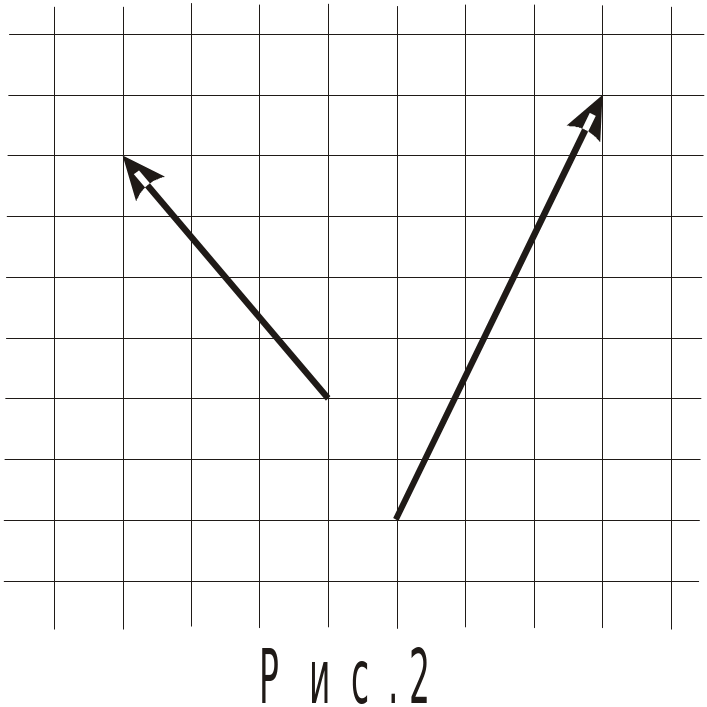 копируйте векторы с рис. 2 в тетрадь и постройте векторы:
копируйте векторы с рис. 2 в тетрадь и постройте векторы: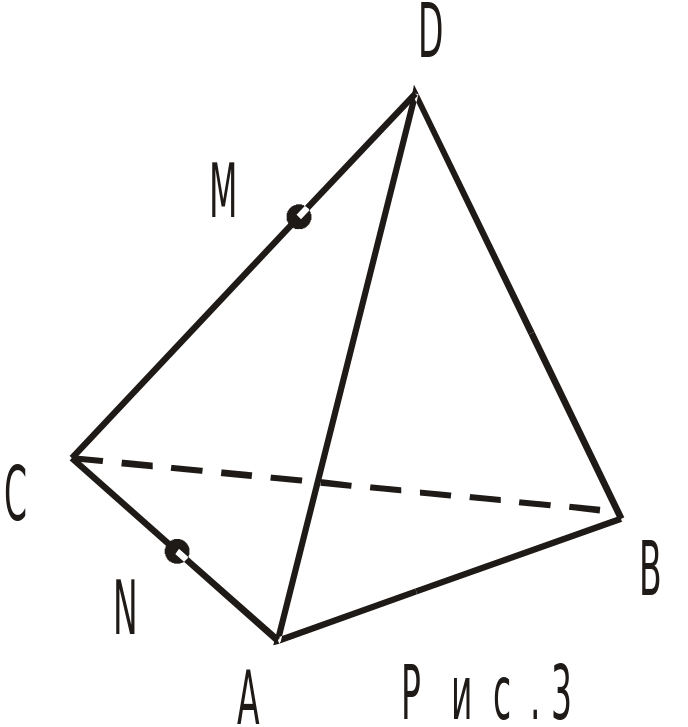 простите выражения: а)
простите выражения: а) 









