Понятие «Задача» и ее структурные компоненты.
При обучении младших школьников решению задач уделяется большое внимание так, как:
в сюжетах отражена конкретная жизненная ситуация, знакомая ребенку, ему легко установить и осознать количественные отношения между объектами.
решение задач помогает осознать ребенку практическую значимость тех математических понятий, которыми он овладевает в начальном курсе математики.
в процессе решения задач у ребенка формируются умения, необходимые для решения любой математической задачи (выделять данные и искомые, условие и вопрос, устанавливать зависимость между ними, строить умозаключения, моделировать, проверять полученный результат).
Определим, прежде всего, что в методике начального обучения подразумевается под задачей. Под задачей в начальном курсе математики подразумевается специальный текст, в котором обрисована некая житейская ситуация, охарактеризованная численными компонентами, имеющими зависимость между собой. Таким образом, текст задачи можно рассматривать как словесную модель реальной действительности.
Пример. За 9 часов полета голубь может преодолеть 657 км. За какое время он, двигаясь с такой же скоростью, долетит от Петербурга до Москвы, если расстояние между городами 730 км?
В задаче описывается движение голубя. Любое движение описывается тремя величинами: пройденным расстоянием, скоростью и временем движения. В данной задаче известно, что расстояние между городами 730 км, дано расстояние, которое может преодолеть голубь за определенное количество времени. Необходимо найти за время, за которое он долетит между городами.
По мнению Н.Б. Истоминой, любое математическое задание можно рассматривать как задачу, выделив в нем условие, то есть ту часть, где содержатся сведения об известных и неизвестных значениях величин, об отношениях между ними и требование, то есть указание на то, что нужно найти [3].
Пример
Поставь знаки =, чтобы получились верные записи 3 5; 8 4.
Условие задачи: числа 3,5,8,4.
Требование: сравнить числа.
Реши уравнение х+4=9.
Выбери из данных прямоугольников те, из которых можно сложить квадрат.
В начальном курсе математики под понятием «задача» подразумевается арифметическая задача. Эти задачи формулируются в виде текста, в котором находят отражение количественные отношения между реальными объектами. Поэтому их называют «текстовыми», «сюжетными», «вычислительными». Основная особенность текстовых задач состоит в том, что в них не указывается какое именно действие (или действия) должно быть выполнено для получения ответа на требование задачи.
Таким образом, задача является носителем какой-либо познавательной информации и обладает следующими свойствами:
проблемность, воздействующая на потребностно-мотивационную сферу учащегося и тем самым стимулирующая его деятельность;
необходимость в интеллектуальных усилиях, организующая систематические умственные упражнения и прививающая «вкус» к интеллектуальному труду, а, следовательно, влияющая на развитие мышления;
неизбежность преобразовательных действий с моделями задач, обеспечивающая усвоение предметного содержания задачи и способствующая развитию продуктивных форм мышления.
Структурные элементы задачи.
Структурными элементами задачи являются: условие, требование, данные и искомое.
Условие - это часть текста, в которой задана сюжетная ситуация, численные компоненты этой ситуации и связи между ними. В стандартной формулировке условие выражается одним или несколькими повествовательными предложениями.
Требование - это часть текста, в которой указана искомая величина (число, множество). В стандартной формулировке учебников начальных классов требование обычно выражено вопросом, начинающимся словом «сколько» и заканчивающимся знаком вопроса.
Данные - это, как правило, численные (числовые) компоненты текста задачи. Они характеризуют количественные отношения предлагаемой в задаче ситуации: значения величин, численные характеристики множеств и отношений между ними. Численные значения величин и численные характеристики множеств обычно обозначены числами. Численные характеристики отношений между ними могут быть обозначены не числом, а словом, например: «в два раза больше», «столько же, сколько в первом» и т. п, В этом случае дети могут «терять» данные и вообще не воспринимать эти численные характеристики как данные. Провоцируется такая ситуация тем, что все тексты в начальной школе содержат данные, выраженные численно, а тексты задач первого года обучения содержат только численные данные. В этом случае ребенок (особенно плохо читающий) «выхватывает» числа из контекста, и выполняет с ними действия практически независимо от ситуации, заданной в условии (чаще всего ориентируясь на «ключевое» слово: улетели, дали, вместе, принесли и т.п.).
Искомое. Нахождение искомого в численном выражении обычно является конечной целью процесса решения арифметической задачи.
В дальнейшем дети будут сталкиваться с другими видами задач, в частности с задачами геометрического характера: на доказательство, на построение, где искомым является либо сам процесс решения (задачи на доказательство), либо результат этого процесса, выраженный не в численных характеристиках (фигура в задаче на построение; буквенное выражение в алгебраической задаче). Задачи последнего вида часто встречаются в учебнике Л.Г. Петерсон, Н.Б. Истоминой. Приведем пример задачи, где процесс ее решения приводит к численному результату, который не является целью решения задачи, а лишь косвенно используется для характеристики неизвестного: «Если цену учебника уменьшить в 3 раза, то получим цену блокнота. Блокнот в 3 раза дороже тетради. Краски в 9 раз дороже тетради. Хватит ли денег, которые мама дала для покупки учебника, на покупку красок?» (учебник Н.Б. Истоминой).
Ответ к данной задаче предполагается в виде: «Денег на покупку красок хватит». Чтобы получить этот ответ, следует установить соотношение между ценами и фактически выразить цену красок в количестве «единичных цен», за которые нужно принять цену тетради.
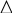
 В учебниках математики для начальной школы встречаются задачи, имеющие различные конструкции. Рассмотрим их.
В учебниках математики для начальной школы встречаются задачи, имеющие различные конструкции. Рассмотрим их.
Обозначим схематически условие , а требование . Задача может иметь одну из конструкций: 1, 2 или 3:
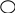
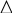 1.
1.
1) Дети пошли в поход. Было 18 мальчиков и 10 девочек. Сколько детей пошло в поход?
2) В один бидон вмешивается 32 л. воды, а во второй – на 12 л. меньше. Найди емкость двух бидонов вместе.
3) Дети посадили 4 куста малины, 5 кустов смородины, а крыжовника столько кустов, сколько малины и смородины вместе. Сколько вместе кустов посадили дети?
4) В оркестре 8 скрипок, а альтов – на 2 меньше. Когда к альтам добавили еще несколько инструментов, то их в оркестре стало 9. Сколько альтов добавили?
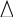

2.
5) Сколько марок подарил Петя, если Сереже он подарил 8 марок, а Коле 5 марок?
6) Сколько пассажиров совершало полет, если в самолете было 25 женщин, мужчин на 15 человек больше, чем женщин, а детей на 10 человек меньше, чем женщин?
7) Сколько карандашей в двух одинаковых коробках, если в одной 2 десятка карандашей?
8) Сколько нужно колес для двух трехколесных велосипедов?
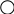

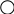 3.
3.
9) Мама испекла 20 пирожков. Сколько пирожков осталось после того, как за ужином съели 15 пирожков?
10) В магазине продали 22 ящика с помидорами. Сколько ящиков с помидорами было, если осталось продать 8 ящиков?
11) Белоснежка вырастила 14 астр и 20 гвоздик. Сколько цветов осталось у Белоснежки после того, как она подарила гномам 7 цветов?
12) Когда отцу было 40 лет, сыну было 12. Найди возраст сына, когда отцу было 52 года.
Такие тексты в методике обучения математике младших школьников принято называть трансформированными. Работа с такими текстами является наиболее полезной с точки зрения обучения решению задач, поскольку именно такие тексты учат ребенка внимательно читать и анализировать задачу, целенаправленно устанавливать связи между данными и искомым с целью осознанного выбора действия. Работа над такими задачами - и есть та перспективная линия, имея в виду преемственность обучения математике.






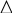
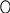 В учебниках математики для начальной школы встречаются задачи, имеющие различные конструкции. Рассмотрим их.
В учебниках математики для начальной школы встречаются задачи, имеющие различные конструкции. Рассмотрим их.