Просмотр содержимого документа
«Задачи № 26 из огэ по математике»
Несколько задач №26 из ОГЭ по математике
1. В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS , если известно, что около четырёхугольника NPQM можно описать окружность, PQ = 12 ,SQ = 9.
Решение:



 Q
Q


 P
P
S
M
N
Из условия угол PNQ = углу QNM, а угол PNQ = углу PMQ как вписанные и опирающиеся на одну дугу, а ∆PQM равнобедренный и PQ = QM = 12. У ∆SQM и ∆NQM NQM общий, QNM = PMQ, значит ∆SQM  ∆NQM по дум углам, а значит сходственные стороны этих треугольников пропорциональны:
∆NQM по дум углам, а значит сходственные стороны этих треугольников пропорциональны: 
Ответ: SN =7.
2. В равнобедренную трапецию, периметр которой равен 120, а площадь равна 540, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
![]()




 Решение: B K C
Решение: B K C
O
R S
А ll D
T L M
Окружность вписана в трапецию, значит из точек A,B,C,D к окружности проведены касательные, которые касаются к окружности в точках RKSL. По свойству касательных отрезки BK = BR, CK = CS, DL = DS, AR = AL. Трапеция равнобедренная, а значит AB = CD AR + BR = CS + SD BC + AD = AB + CD BC + AD = 120: 2 = 60. Площадь трапеции вычисляется как полусумма оснований на высоту. KL = h – высота. Значит (BC + AD)/2 = 540 30h = 540 h = 18. Проведем из точки С перпендикуляр к AD. Длина СM = KL = 18, CD = 30. Треугольник CMD прямоугольный. Найдем в треугольнике катет MD по теореме Пифагора.  Треугольник ATB = MCD, значит AT = MD. AD + BC = 2AT + BC + BC = 60 BC = 6. Тогда AD = 56 В трапеции треугольники BOC и AOD подобны по углам BOC и AOD - вертикальные, углы OCB и OAD накрестлежащие. Сходственные элементы треугольников пропорциональны.
Треугольник ATB = MCD, значит AT = MD. AD + BC = 2AT + BC + BC = 60 BC = 6. Тогда AD = 56 В трапеции треугольники BOC и AOD подобны по углам BOC и AOD - вертикальные, углы OCB и OAD накрестлежащие. Сходственные элементы треугольников пропорциональны.
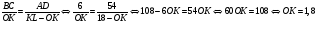
Ответ: OK = 1,8
3. Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K , длина стороны AC относится к длине стороны AB как 9:7. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.



 B
B

 K P
K P
A M C
Решение: Отрезок AP биссектриса угла A как треугольника ABC так и треугольника ABM. Биссектриса любого угла треугольника делит противоположную сторону на части пропорциональные прилежащим сторонам треугольника. Значит AB : BC = PC : PB = 9 : 7. BM – медиана, значит AM = MC = 0,5AC = AM : AB = MK : KB. Пусть площадь треугольника AKM = S, такая же площадь и у треугольника MKC, так как медиана делит треугольник на два равновеликих(одинаковой площади) треугольника. Одинаковые площади по той же причине будут у ABM и MBC. Треугольники AKM и AKB имеют одну высоту, значит SAKM : SAKB = KM : KB; SCKP : SABP = PC : PB. 
 .
.  ,
,
Ответ: 

 4. Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 8, тангенс угла BAC равен
4. Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 8, тангенс угла BAC равен  . Найдите радиус вписанной окружности треугольника ABC. B
. Найдите радиус вписанной окружности треугольника ABC. B
 P
P
 C A
C A
Решение:  Пусть CP = h, тогда
Пусть CP = h, тогда 
 , где
, где  ,
,  , Получим Значит BP =
, Получим Значит BP = 

 Значит
Значит 
 ,
,  ,
,  ,
, 
Ответ: 








 Q
Q

 P
P  ∆NQM по дум углам, а значит сходственные стороны этих треугольников пропорциональны:
∆NQM по дум углам, а значит сходственные стороны этих треугольников пропорциональны: 




 Решение: B K C
Решение: B K C  Треугольник ATB = MCD, значит AT = MD. AD + BC = 2AT + BC + BC = 60 BC = 6. Тогда AD = 56 В трапеции треугольники BOC и AOD подобны по углам BOC и AOD - вертикальные, углы OCB и OAD накрестлежащие. Сходственные элементы треугольников пропорциональны.
Треугольник ATB = MCD, значит AT = MD. AD + BC = 2AT + BC + BC = 60 BC = 6. Тогда AD = 56 В трапеции треугольники BOC и AOD подобны по углам BOC и AOD - вертикальные, углы OCB и OAD накрестлежащие. Сходственные элементы треугольников пропорциональны. 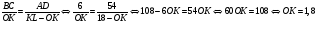



 B
B
 K P
K P
 .
. 









