6 класс
Площадь фигуры. Формула площади прямоугольника. Приближённое измерение площади фигур.
Задача 1. Дачный участок имеет форму прямоугольника, стороны которого равны 50 м и 35 м. Дом, расположенный на участке, также имеет форму прямоугольника, стороны которого равны 8 м и 10 м. Найдите площадь оставшейся части участка, не занятой домом. Ответ дайте в квадратных метрах.

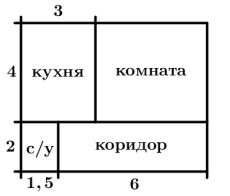
Задача 2. Квартира состоит из комнаты, кухни, коридора и санузла (см. чертёж). Кухня имеет размеры 3 м х 4 м, санузел — 1,5 м х 2 м, длина коридора 6 м. Найдите площадь комнаты (в квадратных метрах).
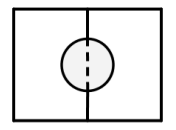
Задача 3. Два садовода, имеющие прямоугольные участки размерами 24 м на 30 м с общей границей, договорились и сделали общий круглый пруд площадью 140 квадратных метров (см. чертёж), причём граница участков проходит точно через центр пруда. Какова площадь (в квадратных метрах) оставшейся части участка каждого садовода?
Задача 4. Пол комнаты, имеющей форму прямоугольника со сторонами 4 м и 6 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 5 см и 40 см. Сколько потребуется таких дощечек?
Задача 5. Вычислите площадь фигуры

Приближённое измерение площади фигур
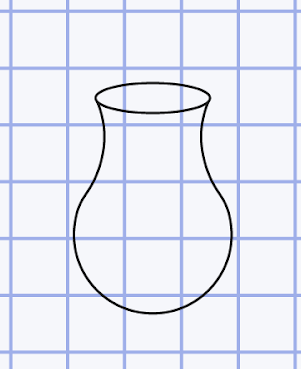
Задача 1. Найдите приближенную площадь вазы
Задача 2. Найдите приближенную площадь лимона

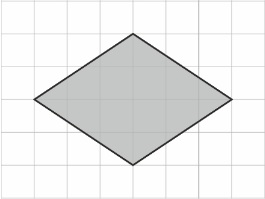
Задача 3. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки 1 см · 1 см. Ответ дайте в квадратных сантиметрах.
Задача 4. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см · 1 см. Ответ дайте в квадратных сантиметрах.
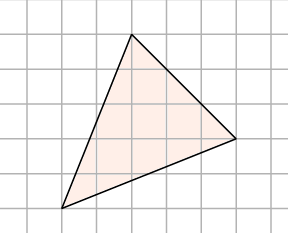
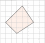
Задача 5. Найдите площадь четырехугольника изображенного на клетчатой бумаге с размером клетки 1 см · 1 см. Ответ дайте в квадратных сантиметрах.
Решение
Задача 1. Дачный участок имеет форму прямоугольника, стороны которого равны 50 м и 35 м. Дом, расположенный на участке, также имеет форму прямоугольника, стороны которого равны 8 м и 10 м. Найдите площадь оставшейся части участка, не занятой домом. Ответ дайте в квадратных метрах.
| Краткое условие | Формулы | Решение |
| Дачный участок, дом (прямоугольник) а, b – длина и ширина участка а=50 м b=35м с, d – ширина и длина дома с= 8 м d= 10 м 
|
S = a · b | 50 · 35=1750 (м2) – площадь участка. 10 · 8 = 80 (м2) – площадь дома. 1750 – 80 = 1670 (м2) - площадь оставшейся части участка, не занятой домом. Ответ: 1670 м2.
|
Задача 2. Квартира состоит из комнаты, кухни, коридора и санузла (см. чертёж). Кухня имеет размеры 3 м х 4 м, санузел — 1,5 м х 2 м, длина коридора 6 м. Найдите площадь комнаты (в квадратных метрах).

| Краткое условие | Формулы | Решение |
| Комната (прямоугольник) a, b – ширина и длина комнаты а = 4м | S = a · b | 6+1,5-3 = 4,5( м) – вторая сторона комнаты 4 · 4,5 = 18 (м2) – площадь комнаты Ответ: 18 м2.
|
Задача 3. Два садовода, имеющие прямоугольные участки размерами 24 м на 30 м с общей границей, договорились и сделали общий круглый пруд площадью 140 квадратных метров (см. чертёж), причём граница участков проходит точно через центр пруда. Какова площадь (в квадратных метрах) оставшейся части участка каждого садовода?

| Краткое условие | Формулы | Решение |
| Участок (прямоугольник) a, b – ширина и длина участка а = 24 м b = 30 м S(пруда) = 140м2 | S = a · b | 30 ∙ 24 = 720 (м2) - площадь одного участка. 140 : 2 = 70 (м2) – площадь половины пруда. 720 – 40 = 650 (м2) – площадь оставшейся части участка каждого садовода. Ответ: 650м2.
|
Задача 4. Пол комнаты, имеющей форму прямоугольника со сторонами 4 м и 6 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 5 см и 40 см. Сколько потребуется таких дощечек?
| Краткое условие | Формулы | Решение |
| Пол комнаты и дощечка (прямоугольник) a, b – ширина и длина пола комнаты а = 4м; b = 6 м с, d - ширина и длина дощечки с = 5 см = 0,05м d = 40 см = 0,4 м | S = a · b | 4 ∙ 6 = 24 (м2) – площадь пола комнаты 0,05 ∙ 0,4 = 0,02 (м2) – площадь дощечки 24 : 0,02 = 1200 (шт.) - потребуется дощечек Ответ: 1200 штук. |
Задача 5. Вычислите площадь фигуры
| Краткое условие | Формулы | Решение |
| 
| S = a · b | 1 способ. Решим задачу методом вычитания площадей фигур. Достроим данную фигуру до квадрата со сторонами 6 см и 6 см.

6 см  
6см
6∙6=36 (см2) – площадь квадрата 4∙2= 8(см2) – площадь прямоугольника 36 – 8 = 28 (см2) – площадь искомой фигуры Ответ: 28 см2. 2 способ. Решим задачу методом сложения площадей фигур. Разобьем данную фигуру на две фигуры. Первая фигура с размерами 4 см и 6 см. Вторая фигура с размерами 2 см и 2 см.   2 см 6 см    
4 см
4 ∙ 6 = 24 (см2) – площадь первой фигуры 2 ∙ 2 = 4 (см2) - площадь второй фигуры 24 + 4 = 28(см2) площадь искомой фигуры Ответ: 28 см2.
|
Приближённое измерение площади фигур
1)Формула приближенного вычисления площади:
S 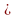 a + (b – a) : 2, где a
a + (b – a) : 2, где a
a – нижняя граница (сколько целых клеток);
b – верхняя граница (сколько всего клеток).
2)Универсальный алгоритм приближенного вычисления площади фигуры:
Наложить на фигуру палетку.
Найти, сколько целых клеток (а) внутри фигуры.
Найти, сколько всего клеток (b) занимает фигура.
Посчитать площадь частично занятых клеток по формуле: (b – a):2.
Вычислить приближенное значение фигуры по формуле:
S 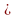 a + (b – a) : 2
a + (b – a) : 2
Запомни, если при вычитании b – a получилось нечетное число (число, которое не делится на 2), то результат надо увеличить на 1.
Записать вычисление в тетрадь, выражая результат в квадратных единицах.
Задача 1. Найдите приближенную площадь вазы

| Краткое условие | Формулы | Решение |
| a = 3, b = 15. 
| S 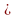 a + (b – a) : 2, где a a + (b – a) : 2, где a a – нижняя граница (сколько целых клеток); b – верхняя граница (сколько всего клеток).
| S 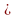 3 + (15 – 3) : 2 = 9 (кв.ед.) 3 + (15 – 3) : 2 = 9 (кв.ед.) Ответ: 9 кв.ед.
|
Задача 2. Найдите приближенную площадь лимона

| Краткое условие | Формулы | Решение |
| a = 5, b = 21. 
| S 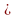 a + (b – a) : 2, где a a + (b – a) : 2, где a a – нижняя граница (сколько целых клеток); b – верхняя граница (сколько всего клеток).
|
S 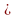 5 + (21 – 5) : 2 = 13 (кв.ед.) 5 + (21 – 5) : 2 = 13 (кв.ед.) Ответ: 13 кв.ед.
|
Задача 3. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки 1 см · 1 см. Ответ дайте в квадратных сантиметрах.
| Краткое условие | Формулы | Решение |
| a = 4, b = 19. 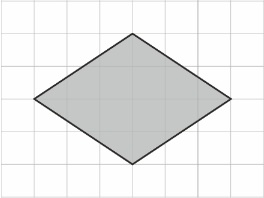
| S 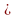 a + (b – a) : 2, где a a + (b – a) : 2, где a a – нижняя граница (сколько целых клеток); b – верхняя граница (сколько всего клеток).
|
S 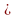 4+ (19 – 4) : 2 = 12 (кв.ед.) 4+ (19 – 4) : 2 = 12 (кв.ед.) при вычитании 19 – 4 получилось нечетное число, то результат увеличили на 1.
Ответ: 12 кв.ед.
|
Задача 4. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см · 1 см. Ответ дайте в квадратных сантиметрах.
| Краткое условие | Формулы | Решение |
| a =4, b = 18 
| S 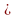 a + (b – a) : 2, где a a + (b – a) : 2, где a a – нижняя граница (сколько целых клеток); b – верхняя граница (сколько всего клеток).
|
S 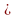 4+ (18 – 4) : 2 = 11 (см2) 4+ (18 – 4) : 2 = 11 (см2) Ответ: 11 см2.
|
Задача 5. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см · 1 см. Ответ дайте в квадратных сантиметрах.
| Краткое условие | Формулы | Решение |
| a =6, b = 18 
| S  a + (b – a) : 2, где a a + (b – a) : 2, где a a – нижняя граница (сколько целых клеток); b – верхняя граница (сколько всего клеток).
|
S  6+ (18 – 6) : 2 = 12 (см2) 6+ (18 – 6) : 2 = 12 (см2) Ответ: 12 см2.
|























 a + (b – a) : 2, где a
a + (b – a) : 2, где a 











